基于混沌小生境粒子群和纹理特征的车牌定位

李 澍

LI Shu

(四川省乐山职业技术学院，乐山 614000)

0 引言

车牌的自动识别是计算机视觉、图像处理与模式识别技术在智能交通领域应用的重要研究课题之一，是实现交通管理智能化的重要环节，主要包括车牌定位、字符分割和字符识别等环节[1]。其中，车牌定位在整个系统中占有非常重要的地位，是整个车牌自动识别系统的关键。目前车辆牌照定位算法主要基于以下几种方法[2]：基于图像彩色信息[3]；基于纹理分析[4]；基于边缘检测[5,6]；基于数学形态学[7]；基于遗传算法；基于神经网络等。然而，在背景复杂、车牌区域变形和噪声污损严重的情况下，用这些方法得到的结果并不十分理想，甚至会产生拒识或误识。针对上述情况，本文提出了基于混沌小生境粒子群的车牌定位算法。考虑到传统的车牌特征提取方法会将车牌区域定位在车灯等其他地方，并且在背景复杂或者噪声严重的情况下，定位的结果很不理想，会产生拒识或误识等问题。本文研究了车牌区域的重点特征，提取7种能够准确反映车牌区域的特征向量，构成整个车牌的特征矢量。

1 车牌区域的特征提取

从人眼视觉的角度出发，牌照的字符目标区域具有如下特点：1）牌照的字符与底色在灰度上有较大差异，而字符与牌照底的内部灰度较均匀。2）牌照字符有多个，基本呈水平排列，所以在牌照的矩形区域内存在较丰富的边缘。3）不同图像中牌照的具体大小、位置不确定，但大小变化有一定范围，存在一个最大长度和高度。图1(a)是一幅随即抽取的样本图像（大小为640×480,256灰度级），图1(b)为样本图像车牌区域的灰度变化曲线图（横坐标代表车牌行位置，纵坐标代表灰度），可以看出，在牌照区域，灰度曲线变化剧烈，高灰度值与低灰度值之间的差异较大，且波峰波谷有一定的间隔，个数也相对稳定，与其他区域相比有明显的区别。

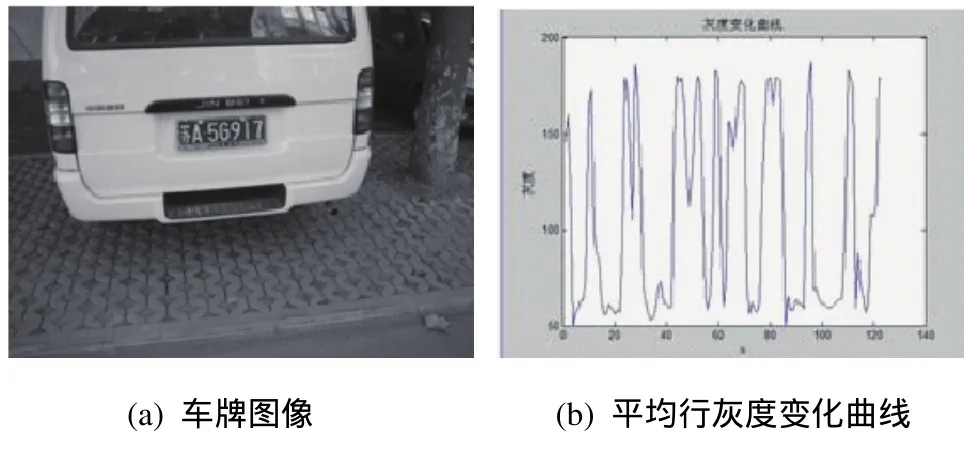
因此，在图像上随机确定一个矩形区域，其左上角顶点的坐标为(x,y)，长度为l，高度为h，对该区域里的每一行灰度值进行一维的波峰检测和波谷检测，然后统计检测到的波峰波谷，得到车牌区域的7个特征：1）波峰的密度Den；2）波峰的均值Mp；3）波峰波谷的均值差Mpt；4）波峰绝对差Ap；5）波谷绝对差At；6）波峰间距的绝对差Ad；7）区域平均每一行的波峰个数Np。大量的统计实验表明，这7个特征组成的特征向量V具有较小的类内距离和较大的类间距离，而且只与区域灰度的波峰波谷有关，比起传统的用灰度直方图分析的方法，其对噪声的敏感度大大降低。

根据上面的7个特征，得到车牌的特征矢量V：

对于车牌特征矢量V，前三个特征值应该较大，后面的三个特征值应较小，最后一个特征值理论上相对稳定，应该为14（一般车牌有7个字符）。

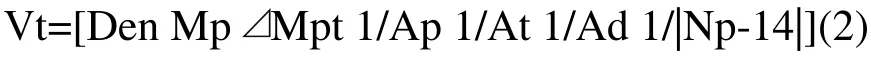
然而，Vt中各分量并不具有相等的重要性，例如波峰密度比间距绝对差对类内距离的贡献更大。因此，将Vt进行线性变换，变换后，重要的特征赋予较大的权值，不重要的特征给予较小的权值。假定变换矩阵为对角阵，即：

式(3)中，σ2j为模式分量vj方向的样本方差。可以看出，方差较小的对应加权系数大，标志相应的特征更加可靠；相反，方差较大的对应加权系数小，标志相应的特征可靠性弱。因此，变换矩阵W将模式向量由Vt空间变换到U空间。

从不同大小、不同位置提取出的特征矢量组成集合{}iU，其中最佳的特征向量U*值代表了车牌区域，评价准则为

从上面看出，该方法的车牌定位最终归结为确定矩形区域的位置参量x、y，长度参量l，高度参量h，使其得到的特征矢量为最佳。这个全局搜索问题，如果采用遗传优化算法，由于其无记忆性，且容易陷入早熟，搜索到最佳值可能不是全局最优解，从而影响到结果的准确性，计算了也偏大。故本文采用基于混沌变异的小生境粒子群算法搜索最佳特征矢量。

2 基于混沌变异的小生境粒子群算法

2.1 基本粒子群算法

设在n维解空间中，每个粒子i有位置Xi=(Xi1,Xi2,…,Xin)和速度Vi=(Vi1,Vi2,…,Vin)，前者表示问题的解，对应的目标函数值pfiti作为评价该粒子优劣程度的适应度；后者表示粒子从当前位置移动到下一个位置的速度大小。算法首先对粒子群进行初始化，然后通过迭代方式在解空间中寻找最优解。假设在第t次迭代时刻，粒子i的最优解为pbesti (t)，称为个体极值，整个粒子群的最优解为gbest(t)，称为全局极值。在t+1时刻，按下式更新自己的速度：

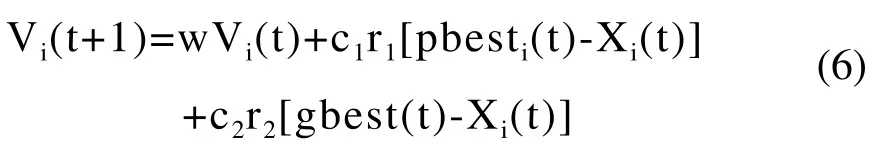
然后以速度Vi(t+1)移动到下一个位置，即:

其中t表示当前迭代次数，学习因子c1=c2=2；r1、r2是均匀分布在(0,1)上的随机数；惯性因子w设为：w=wmax- t×(wmax-wmin) /tmax，其中tmax表示总迭代次数， wmax和wmin分别表示最大和最小惯性因子，本文wmax=0.95，wmin=0.4。迭代更新过程中，粒子的速率限制在[Vmin，Vmax]，Vmin=-Vmax=-8。位置限制在允许范围内，最后输出的gbest为全局最优解。

2.2 基于混沌变异的小生境粒子群算法

基本粒子群算法实现简单，需要确定的参数少，但它容易陷入局部极值，搜索精度还不够高。结合小生境策略全局优化与变尺度混沌变异精细搜索两者优点的混沌小生境粒子群算法，可避免算法早熟，保证搜索精度。本文使用的混沌映射Logistic迭代方程为：

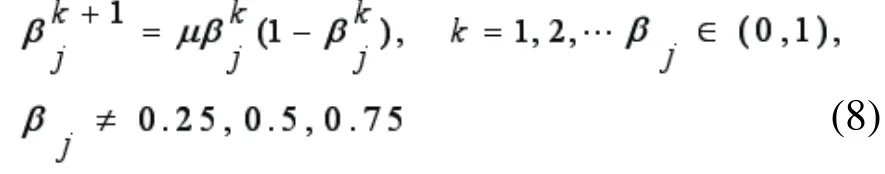
在迭代过程中，按下列方程对每个小生境种群中的最优个体pbesti(t) =[ X1, X2,…, Xj…, Xn]进行混沌迭代变异：

其中，λg称为收缩因子，它决定了变量Xj的变异空间，由下式得到：

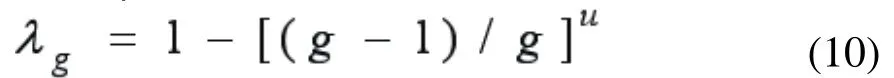
式中，g为粒子群的进化代数，u用于控制收缩速度，本文中u=2。

现利用基于混沌变异的小生境粒子群算法搜索最佳阈值，算法具体步骤如下：

1）初始化小生境粒子种群。随机产生m个粒子，并分成n个子种群。[x,y,l,h]作为每个粒子的位置，粒子速度在[,]minmaxVV上随机产生；工程中，车辆与摄像头的距离可以通过硬件设施设定，在对大量样本统计后，可以将车牌大小定为120 ≤l ≤130,38 ≤h≤42，位置范围也可确定为max max1 ≤x ≤680×l ,240 ≤y ≤480×h。240为图像高度的一半，这里利用车牌一般在图像下半部的先验知识。

2）设计粒子群的适应度函数。当区域对应的矢量范数很大，且区域的形状与车牌的形状相似时即得到了真实的车牌区域。因此构造适应度函数f(x,y,l,h)为：

根据式(11)适应度函数找出每个小生境种群中的最优粒子和全局最优粒子；

3）计算两个粒子种群最优个体pbesti(t)与pbestj(t)之间的距离dij。若dij＜ Rniche(小生境半径)，比较两个小生境最优个体的适应度，低者置零，高者保持不变。对置零的最优个体重新初始化，并在其所在的小生境内重新选择最优个体，直至任意两个小生境最优个体之间的距离dij≥Rniche；

4）如果迭代次数达到预定值，则对最劣小生境子种群进行更新初始化；

5）按式(9)对所有小生境最优个体的位置进行变尺度混沌变异，进一步提高搜索精度；

6）更新每个粒子的位置和速度；

7）如果满足结束条件，则停止迭代，输出最佳特征矢量，并根据该矢量精确提取出车牌，否则转2)。

3 结果分析

为了验证算法的有效性，本文对大量车牌图像进行了实验。并与基于遗传算法和基本粒子群算法的定位结果进行了比较，说明了本文方法的稳定性和准确性。因篇幅有限，现选取其中4幅图像作为例子加以说明。

(a) (b)

(c) (d)图2 随机抽取的4幅实验图像

图3 三种方法的定位结果

图2中4幅图像为随机抽取的车牌样本，大小均为640×480,256灰度级，(a)、(b)两幅图像干扰因素小，理论上应该三种方法都能准确提取；(c)图像的车灯处近似于车牌特征矢量，对定位结果产生很大干扰；(d)图像不仅车灯处，车牌上方的排风扇也与车牌特征矢量相近，对准确定位带来很大难度。图3中从上到下分别对应图2中4幅图像基于不同方法定位的结果，从左往右分别是基于遗传算法、基本粒子群算法和本文的混沌小生境粒子群算法的定位结果。可以看出，对于(a)、(b)图像，三种方法基本都能准确分割；对于(c)图像，遗传算法和基本粒子群算法都有一定的概率将车牌定位在了车灯处，也就是优化搜索过程中，找到的是局部最优，而非全局最优，也反映了遗传算法容易“早熟”，基本粒子群算法容易陷入局部最优的缺点，而本文的混沌小生境粒子群算法能够准确定位到车牌位置；(d)图像的遗传算法存在一定概率将车牌定位在车灯处，基本粒子群算法存在一定概率将车牌定位在了车牌上方的排风扇处，这还是体现了这两种算法在优化搜索的过程中的缺陷，本文方法依然能够准确定位，不受干扰因素的影响，这也说明了基于混沌变异的小生境粒子群算法在搜索全局最优解的过程中，避免了算法早熟或者陷入局部最优，使得最终的结果一定是全局最优，也就能够准确提取车牌。

4 结束语

分析表明，本文提取的7种车牌特征向量能够准确唯一地反映了车牌区域的特点，将其作为提取车牌的参考标准，提取的准确度高，不易受噪声，变形等复杂情况的干扰；采用的混沌小生境粒子群算法在保证搜索精度的同时大大降低了四维空间的搜索代价，提高了运行速度，与基于遗传算法、基本粒子群算法的定位方法相比，本文方法在定位精度和运算时间上都有明显的优势。

[1] SONG H SH,WANG G Q.The high performance car license plate recognition system and its core techniques[C].Proceedings of IEEE International Conference on Vehicular Electronics and Safety,2005:42-45.

[2] 袁宝明,于万波,魏小鹏.汽车牌照定位综述[J].大连大学学报,2002,23(2):6-12.

[3] 曾丽华,李超,熊璋.基于边缘与颜色信息的车牌精确定位算法[J].北京航空航天大学学报,2007,33(9):3110-3115.

[4] 赵兵,鲁敏,匡纲要,于慧颖.基于混合特征的车牌定位算法[J].计算机工程与设计,2007,28(23):5668-5670.

[5] 李庆庆,张燕平.基于模糊边缘检测算法的车牌定位[J].计算机技术与发展,2006,16(12):7-9.

[6] ZHENG D N,ZHAO Y N,WANG J X.An ef fi cient method of license plate location[J].Pattern Recognition