汽流偏角对蒸汽湿度测量的误差分析

钱江波，张美凤，李恒凡，韩中合

(华北电力大学 电站设备状态监测与控制教育部重点实验室，河北 保定 071003)

0 引言

电力工业是世界各国的基础工业，汽轮机在电力工业中占据重要地位，据统计，2003年我国总发电量19 052.08亿kW·h，以汽轮机为主体的火电和核电占85.17%[1]。在今后相当长的一段时间内，汽轮机仍将作为电力工业的主要动力装置。火电厂大功率凝汽式汽轮机低压缸的末几级和水冷堆核电汽轮机的全部级都工作在湿蒸汽区，蒸汽带水一方面会使机组效率降低，另一方面会对透平低压级组动叶片产生强烈的侵蚀与冲击，导致叶片表面出现凹坑甚至扭曲断裂，严重威胁汽轮机的安全运行[2～5]。

湿蒸汽给汽轮机运行经济性和可靠性方面带来的损失不可低估，据估计，在英国，由于透平中蒸汽湿度引起的级效率降低造成的经济损失每年就达到5 000万英镑[6]。因此，汽轮机内湿蒸汽问题一直是国内外众多学者给予极大关注的研究课题，蒸汽湿度的准确测量有助于了解湿蒸汽区级的工作状态以及对动叶片的湿汽侵蚀情况进行估算，为汽轮机设备的安全经济运行以及优化设计和结构改进提供指导与参考。

微波谐振腔微扰法测量蒸汽湿度是一种利用湿蒸汽的介电常数来测量蒸汽湿度的方法[3]。为使测量结果能准确反映汽轮机末级后的排汽湿度，要求汽轮机末级排汽速度方向和谐振腔的中轴线方向一致。由于谐振腔在安装过程中不可避免的存在安装偏角，且汽轮机处于变工况运行时，排汽速度会偏离设计工况，使汽轮机排汽速度方向和谐振腔中轴线方向存在偏角。为了准确研究汽流偏角对湿度测量误差的影响，模拟计算了一定排汽压力和颗粒尺寸下，不同汽流偏角和不同排汽速度对湿度测量误差的影响。

1 微波谐振腔的数学模型

微波谐振腔微扰法测量蒸汽湿度的基本思想是基于微波谐振腔的微扰，即微波谐振腔的谐振频率随腔内电介质的介电常数变化将发生偏移，在一定温度 (或压力)下，蒸汽的湿度不同其介电常数也不同，一定温度、压力下湿蒸汽的介电常数只与其湿度有关。当湿蒸汽流过微波谐振腔时，通过测量谐振腔谐振频率的偏移可以测量湿蒸汽的介电常数，进而确定蒸汽的湿度。

微波谐振腔传感器是一个两端开口的圆筒形腔体，在两端开口处设置有等距离等厚度圆环组成的环形栅格分隔器，这种型式的分隔器结构既可以保证湿蒸汽两相流自由通过谐振腔，又保证谐振腔具有较高的品质因数。取样进口附近是复杂的三维湍流流动，由于谐振腔和取样前端是轴对称结构，带楔形取样前端的谐振腔的二维结构如图1所示。

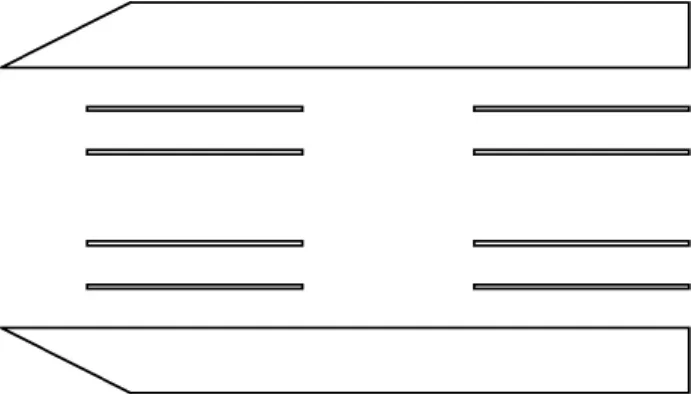
图1 楔形入口的谐振腔纵向剖面图Fig.1 The longitudinal diagram of microwave cavity with wedge-shaped entrance

1.1 微波谐振腔测量蒸汽湿度的公式推导

汽轮机内湿蒸汽中的水分由雾珠和散布的细小水滴组成，大部分水分是通过自发凝结增长生成的、直径为1～2 μm离散分布的雾珠，这部分水滴的数量巨大 (可达107个/cm3)，占湿蒸汽中液相质量的90%以上，这类水滴其直径很小，相对于蒸汽基本没有滑移，随蒸汽一起流动;另一小部分是沉积在叶片表面上的小部分雾珠凝聚成的水膜，在叶片出口边周期性被撕裂形成的“粗糙”水，在低压透平中典型尺寸为直径在10 μm～200 μm范围，在汽轮机排汽中粗糙水仅占总水分的 2% 左右[5，7，8]。

定义蒸汽的体积湿度为Φ，设圆柱形谐振腔的半径为 R，不存在汽流偏角导致的取样误差时，离散相的体积流量为 v=m/ρf，其中 m为离散相的质量流量，ρf为离散相的密度;体积湿度为φ=v/Vv，其中Vv为蒸汽的体积流量，存在汽流偏角 θ时，离散相的体积流量为 v'=(R+r)2vcosθ/R2，式中r表示谐振腔半径与取样汽流半径之差，体积湿度为φ'=v'/Vv。

体积湿度相对误差

1.2 谐振腔两相流模拟的控制方程

1.2.1 汽相控制方程

汽相控制方程[9]的通用形式如下:

式中:ρ，φ，Γ，v，s分别为流体的密度、通用变量、扩散系数、速度矢量和源项。

在三维圆柱轴对称坐标系中，汽流在各个方向的分量为u、v和w，则式 (2)展开得:

连续性方程:

动量方程:

式中:s为源项。

湍流模型k方程:

湍流模型ε方程:

式中:Gk表示单位体积 k的产生率;系数 C1，C2分别取 1.44，1.92[10]。

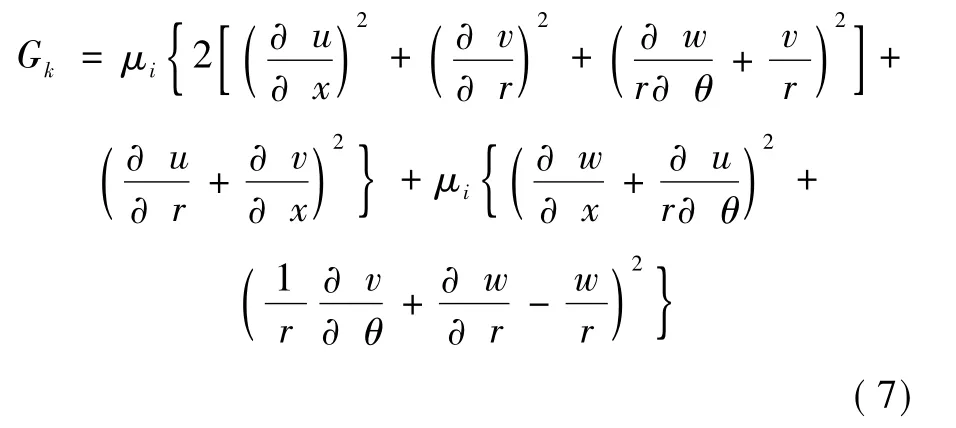
能量方程:

式中:h，Γh分别为比焓和比焓交换系数。

采用Yong[11]提出的蒸汽状态方程:

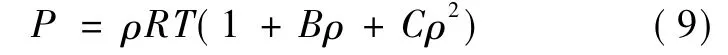
采用基于控制体的有限体积法将上述微分方程组离散化转换为代数方程组。该方法在每一个控制体内积分控制方程，从而产生基于控制体的每个变量都守恒的离散方程。以标量ψ的定常状态守恒方程说明控制方程的离散，对于控制体V的积分方程如下:

式中:A，Γψ，▽ψ，Sψ分别为曲面面积矢量、ψ的扩散系数、ψ的梯度和每一单位体积ψ的源项。

1.2.2 液相控制方程

采用拉格朗日方法计算水滴的运动轨迹，为了简化问题，作如下假设[9]:

(1)水滴与蒸汽间无传热和传质过程，且不发生相变;

(2)水滴为均一尺寸的圆球，均匀分布;

(3)水滴与谐振腔器壁面碰撞即被捕获，不存在反弹;

(4)水滴之间不存在碰撞、聚合、撕裂。

水滴的运动轨迹与水滴的受力情况有关，蒸汽对水滴表面有曳力。在汽轮机末级的排汽中大量存在的是亚观尺寸 (0.01～2 μm)的水滴，适合采用Stokes曳力公式[12]。水滴的作用力平衡方程在直角坐标系下 (x方向)为

对于亚观粒子，其他作用力Fx中，布朗力分量不可忽视。

对方程 (11)积分就得到了水滴轨道上每一个位置的颗粒速度，颗粒轨道通过下式得到:

沿着每个坐标方向求解方程 (12)就得到了离散相的轨迹。

2 网格结构和数值模拟结果

2.1 计算区域的网格结构

带楔形取样端的谐振腔，楔形结构入口角度为26.5°，计算区域的物理结构和网格划分如图2所示，由于计算区域的对称性，计算模型简化为谐振腔纵向剖面，谐振腔壁面设置为墙面边界条件，其余边界设置为压力远场边界条件，主蒸汽压力为5 kPa，主蒸汽温度为306.3 K;计算区域采用四边形结构化网格划分，网格数量为150 329。

图2 计算区域的网格结构Fig.2 The grid structure of the calculation region

2.2 流场的数值分析

采用计算流体力学通用软件FLUENT进行数值模拟，计算工况的颗粒尺寸d=0.5 μm，马赫数分别取0.2，0.3，0.4，0.5，0.6，汽流偏角θ分别取 5°，10°，15°和 20°。

当 d=0.5 μm，θ=15°时，马赫数 Ma=0.2的计算结果如图3所示，马赫数Ma=0.5的计算结果如图4所示;当 d=0.5 μm，马赫数 Ma=0.4时，θ=10°的结果如图5所示，θ=20°时的计算结果如图6所示。体积湿度误差如图7所示。

图3 Ma=0.2，d=0.5，θ=15°的水滴轨迹Fig.3 The droplet trajectory when Ma=0.2，d=0.5，θ=15°

图4 Ma=0.5，d=0.5，θ=15°的水滴轨迹Fig.4 The droplet trajectory when Ma=0.5，d=0.5，θ=15°

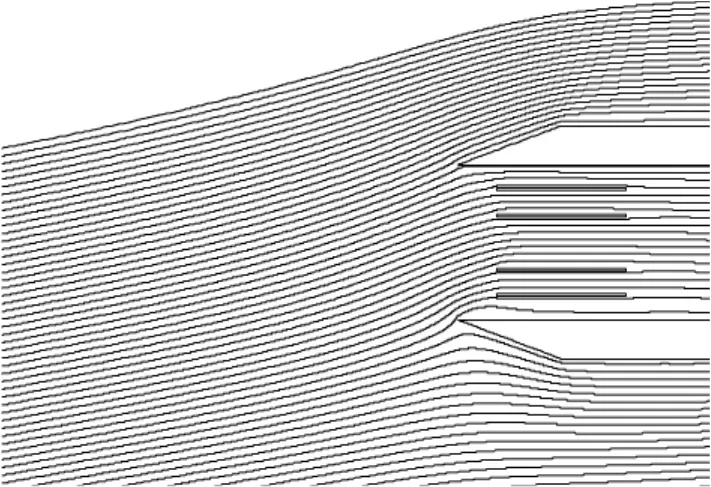
图5 Ma=0.4，d=0.5，θ=10°的水滴轨迹Fig.5 The droplet trajectory when Ma=0.4，d=0.5，θ=10°

图6 Ma=0.4，d=0.5，θ=20°的水滴轨迹Fig.6 The droplet trajectory when Ma=0.4，d=0.5，θ=20°

图7 测量误差Fig.7 The measurement error

3 结果分析

由图7可知，测量误差不仅与汽流偏角有关，而且与蒸汽流速有关。当θ＜10°时，测量误差主要受偏角的影响，受蒸汽流速的影响很小，且随着偏角的增大，测量误差增大;当偏角0°＜θ＜5°时，湿度测量值大于真实值，当5°＜θ＜20°时湿度测量值小于真实值，偏角越大，测量误差越大;当10°＜θ＜20°时，由于楔形取样口附近压力分布受流速的影响，所以壁面对不同流速下水滴的阻挡作用不同，取样误差受蒸汽流速的影响比较明显。

微波谐振腔测量蒸汽湿度时，由于谐振腔壁面的阻挡，水滴绕过谐振腔的取样端，当气流偏角较小 (0°＜θ＜5°)时，由于偏角的存在使一部分绕出的水滴进入到谐振腔内，导致测量值偏大; 当 5°＜θ＜20°时，由 v'=(R+r)2vcosθ/R2可知，测量值受汽流偏角的影响较大，汽流偏角越大，测量值越小，误差越大;由图3～4可知，当10°＜θ＜20°时，由于流动的不稳定性和涡流的影响，使测量误差与蒸汽流速和汽流偏角都有关系;由图5～6可知，蒸汽流速相同时，汽流偏角对测量误差的影响较大，汽流偏角较大时，谐振腔取样端对流场的扰动较大，进入谐振腔内部的水滴数量少，测量值小于真实值，测量误差较大。

减小谐振腔的安装偏角，提高安装精度，能有效减小微波谐振腔测量湿度的误差。实际电厂处于变工况运行时，不可避免的存在汽流偏角，导致排汽湿度测量必然存在偏差，当汽流偏角θ＜10°时，体积湿度的测量误差小于10%，假设汽轮机末级排汽湿度为15%，则湿度取样误差仅为0.15%，取样精度很高;当汽流偏角10°＜θ＜20°，体积湿度的测量误差小于35%，相同排汽湿度下，取样误差仅为5.25%，取样精度较高，能基本代表主流的湿度信息，满足工程实际的需求。

4 结论

(1)微波谐振腔测湿精度受多种因素的影响，不同蒸汽流速和汽流偏角下，影响因素不同。为使测量结果能准确反映汽轮机末级的排汽湿度，测量精度高，必须充分考虑取样的代表性，减小汽流偏角的影响。

(2)当汽流偏角较小时，测量误差主要受偏角的影响，而受蒸汽流速的影响较小;当汽流偏角达到某一临界值时，测量误差受蒸汽流速的影响明显。

(3)当汽流偏角θ＜20°时，体积湿度的测量误差较小，测量精度较高，能满足工程实际的需要。

(4)流场的数值模拟结果表明，通过减小谐振腔的安装偏角，提高安装精度，能有效减小湿度测量的误差，提高测量精度。

(5)实际电厂中的机组经常处于变工况运行，通过进行汽流偏角的修正，能有效减小湿度测量误差，提高测量精度。

[1]中国电力企业联合会．资源节约:电力工业的可持续发展之路[C]．中国科协2004年学术年会论文集，2004:852－855．

[2]韩中合，杨昆．汽轮机中蒸汽湿度测量方法的研究现状[J]．华北电力大学学报，2002，29(4):44－47．

[3]韩中合，张淑娥，田松峰，等．汽轮机排汽湿度谐振腔微扰测量法的研究[J]．中国电机工程学报，2003，23(12):199－202．

[4]王升龙，杨善让，王建国，等．汽轮机排汽湿度的在线监测方法及工业试验研究[J]．中国电机工程学报，2005，25(17):83－87．

[5]黄雪峰．湿蒸汽两相流湿度测量方法研究进展[J]．电站系统工程，2006，22(5):1－4．

[6]Guha A．Computation，analysis and theory of two-phase flows[J]．The Aeronautical Journal，1998，102:71－82．

[7]汪丽莉，蔡小舒．汽轮机湿蒸汽两相流中水滴尺寸研究进展[J]．上海理工大学学报，2003，25(4):307－312．

[8]蔡颐年，王乃宁．湿蒸汽两相流[M]．西安:西安交通大学出版社，1983．

[9]钱江波．蒸汽湿度测量方法研究及实验系统设计[D]．保定:华北电力大学，2004．

[10]Laali A R，Courant J J．Calculation and measurement of fog droplet size:comparison between nuclear and fossil fired turbine[J]．Design，repair and refurbishment of steam turbine of ASME，1991，6(13):45－48．

[11]Young J B．An equation of status for steam for turbomachinery and other flow calculations[J]．Journal of Engineering for Gas Turbines and Power， 1988， 110(1):1－7．

[12]Ounis H，Ahamadi G，Mclaughlin J B．Brownian diffusion of submicrometer particles in the viscous sublayer[J]．Journal of Colloid and Interface Science，1991，143(1):266－277．

[13]Li A，Ahamadi G．Dispersion and deposition of spherical particles from point sources in a turbulent channel flow[J]．Aerosol Science and Technology，1992，16(8):209－226．