基于Lame方程研究非线性Schrödinger方程的行波解
2012-10-08相春环
相春环
(重庆文理学院数学与财经学院,重庆 永川 402160)
近年来探索非线性偏微分方程的解析解,即可积性问题的研究已成为非线性数学物理领域学者研究的一个热点[1-3].由于非线性偏微分方程可以较近似的描述很多非线性物理现象,从而被物理学、生物学、化学、工程建设等方向用作模型.本文研究的非线性Schrödinger方程就是一个被应用在众多方向(热力学、非线性光学、非线性声学、量子凝聚物质等)且被广泛研究的非线性偏微分方程,特别是在玻色-爱因斯坦凝聚的研究中,该方程的应用就是被关注的重要见证之一[4-5].另外,关于高温超导和冷原子在光格子上实验理论和应用研究这一竞争非常激烈的热点问题也涉及该方程的应用[6].数学工具的实际应用深刻地揭示了数学、物理学等领域中许多不同分支之间的一些相互联系,更重要的是其中所涉及的新思想,特别是一些新的代数结构,为物理学相关问题的研究提供了更广泛的基础.本文从Lame方程[7]的角度,并借助椭圆方程研究了非线性Schrödinger方程的行波解.
1 关于Lame方程
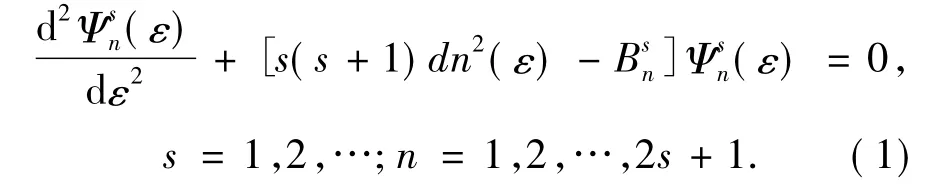
2 非线性Schrödinger方程的行波解
非线性Schrödinger方程是科学研究中一个重要的方程,其一般形式表示如下:
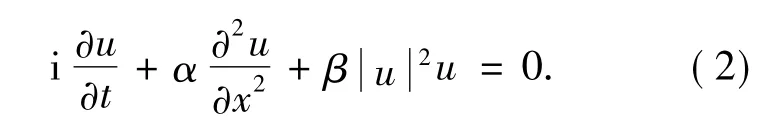
方程(2)中α和β是两个常参数系数,其中α是色散频率系数,β是朗道系数.在不失一般性的条件下可设非线性Schrödinger方程的通解如下:
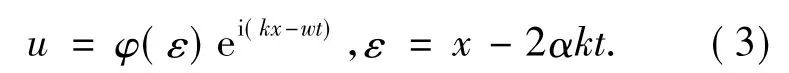
k和w分别为波数和频率.将(3)式代入(2)式可得如下形式的方程:
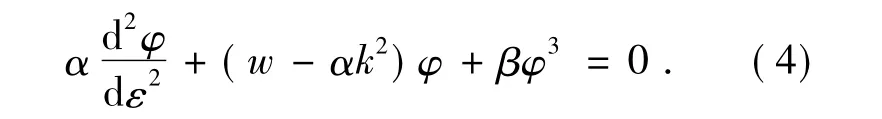
由微扰展开法的知识可得方程(4)波函数的无穷项展开式:
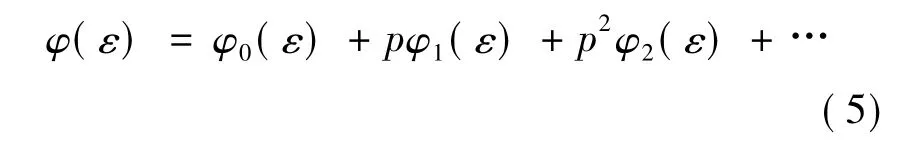
上式中,pn(0 < p<1),n=0,1,2…为相应项的系数,φ0、φ1和φ2分别对应方程(4)的零阶解、一阶解和二阶解.
把方程(5)代入(4)式,经过整理可得形式
如下含有相应阶数的方程:
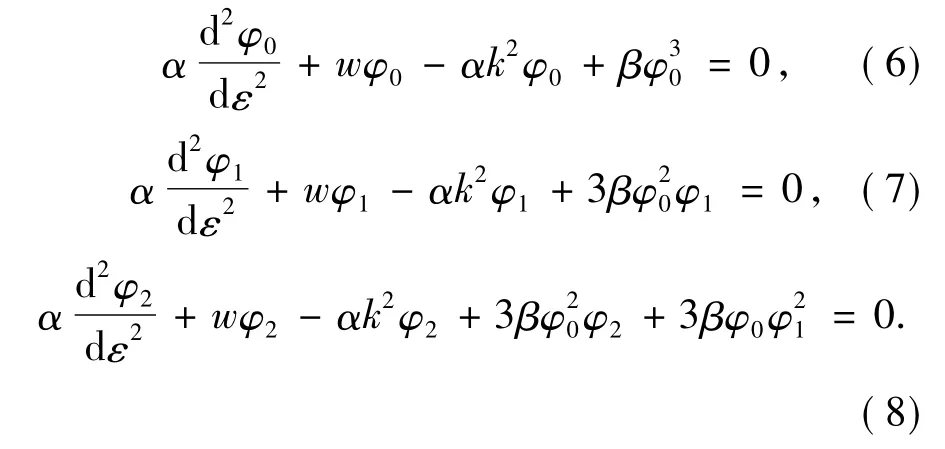
方程(6)的解可用第三类椭圆函数的形式设为:
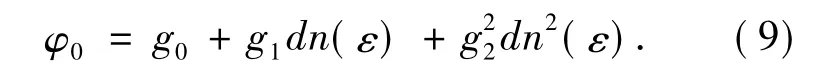
上式中,g0、g1和g2是待定系数.将(9)式代入方程(6),并把各次方的系数合并等零可得:
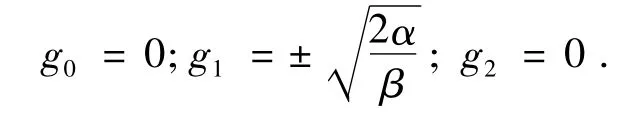
故方程(4)的零阶解在w,k,α,q满足w-αk2=(q2-2)α的条件时可表示为:
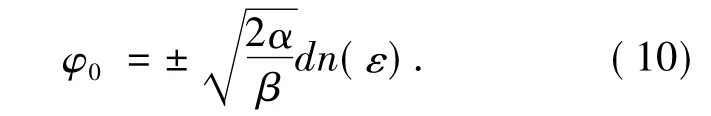
把方程(10)代入方程(7),可得如下方程:

如果设s=2和n=2,借助于方程(1),我们可得方程(11)的本征值为:2-q2.参考文献[9]可得方程(11)的本征函数:
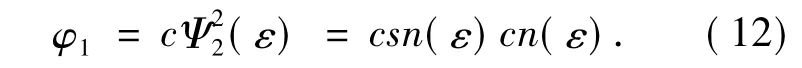
其中,c是一个常数参数.将方程(10)和(12)代入方程(8),关于方程(4)的二阶解的方程可写为:
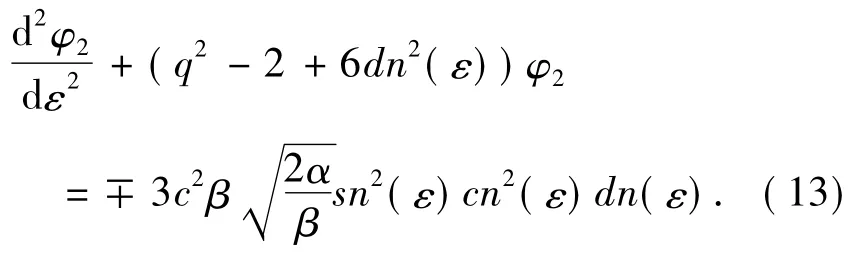
基于上面的讨论,这里假设方程(13)解的形式如下:
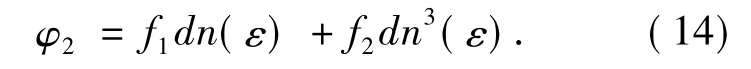
这里f1和f2为待定系数.把方程(14)代入方程(13)并合并dn各次方项的系数可得:

把方程(15)代入(14)可得方程(13)的最终解的形式:
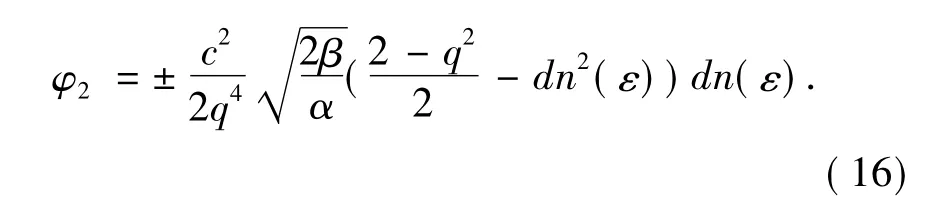
将方程(10)、(12)和(16)代入方程(3)得到非线性Schrödinger方程的最终行波解为:
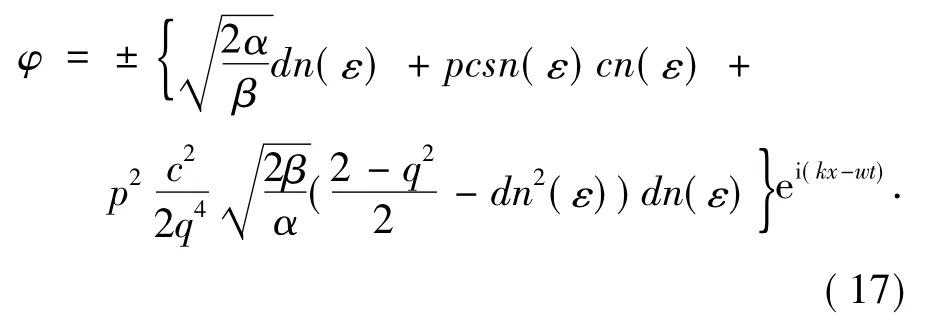
当模数q→0时,椭圆函数作如下退化:

当模数q→1时,椭圆函数可化作双曲函数表示:

将(18)式和(19)式分别代入非线性Schrödinger方程的行波解(17)可得:
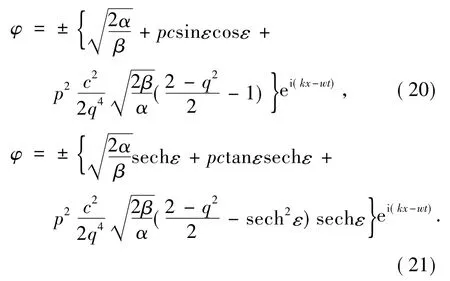
方程(17)、(20)和(21)分别为非线性Schrödinger方程的椭圆函数解、三角函数解和双曲函数解.
3 结论
本文借助Lame方程和椭圆函数方程得到了非线性Schrödinger方程的行波解,并在椭圆函数的模数趋于两种极限的情况下得到了由椭圆函数演变的行波解:三角函数解和双曲函数解.通过对上述行波解的分析,我们可容易得到非线性Schrödinger方程在某特殊点的解析解及其所描述现象的物理可观测量.相因子是波函数的一个重要方面,通过测量相因子可以测得不同参数的相位,借助数值模拟探测模型对称破缺的行为,进而印证解析的正确性.这3类精确行波解可提示并帮助研究应用该方程的学者对可以用非线性Schrödinger方程描述的物质结构有更新的认识.同时,本文获得非线性Schrödinger方程行波解的简捷过程是解相关非线性偏微分方程的得力工具.
[1]Xu Bin,Liu Xiqiang.Symmetries,reductions,group invariant solutions of(2+1)-dimensional Gardner equation[J].Chinese Journal of Quantum Electronics,2009,26(5):531-536.
[2]Taogetusang,Sirendaoerji.Jacobi elliptic function exact solutions of sine-Gordon equation[J].Chinese Journal of Quantum Electronics,2009,26(3):278-287.
[3]Zhu Jiamin,Ma Zhengyi.Exact solutions for the cubic-quintic nonlinear Schrödinger equation[J].Chaos,Solitons & Fractals,2007,33(3):958-964.
[4]Dodd R J.Approximate solutions of the nonlinear Schrö dinger equation for ground and excited states of Bose-Einstein condensates[J].Journal of Research of the National Institute of Standards and Technology,1996,101:545.
[5]Xue Jukui,Zhang Aixia,Liu Jie.Self-trapping of Bose-Einstein condensates in an optical lattice:the effect of the system dimension[J].Physical Review A,2008,77:013602-4.
[6]Frits Beukers,Alexa van der Waall.Lame equations with algebraic solutions[J].Journal of Differential Equations,2004,197:1-25.
[7]Baldassarri F.On algebraic solutions of Lames differential equation[J].Journal of Differential Equations,1981,41:44-58.
[8]Liu Guanting.Lame equation and asymptotic higherorder periodic solutions to nonlinear evolution equations[J].Applied Mathematics and Computation,2009,212:312-317.
[9]Churchill R C.Two-generator subgroups of SL(2,C)and the hypergeometric,Riemann,and Lame equations[J].Journal of symbolic Computation,1999,28:521-545.
[10]Fu Zuntao,Mao Jun,Liu Shida.Multi-order exact solutions to the Drinfeld-Sokolov-Wilson equations[J].Physics Letters A,2009,373:3710-3714.
[11]Wang Zhuxi,Guo Dunren.Special Functions[M].Beijing:Peking University Press,2000:565-573.
[12]Liu Shikuo,Liu Shida.Nonlinear equations in physics[M].Beijing:Peking University Press,2000:294-297.
