移动Ad Hoc网络环境下基于风险的高效可靠的服务组合方法研究*

胡海洋 ，吕 倩 ，俞东进 ，赵格华

（1.杭州电子科技大学计算机学院 杭州 310018；2.南京大学软件新技术国家重点实验室 南京 210093；3.香港中文大学计算机科学与工程系 香港）

1 引言

服务组合是指将现有的单一、功能简单、可执行的服务组合成新的复杂的服务。所谓服务，指的是任何可以被其他设备利用的现有设备上的软件组件、数据以及硬件资源等。例如，使用手机上的天气预报软件可以为手机用户提供天气情况，这就是一个服务。

如今，移动设备功能的不断完善以及无线网络的快速发展，使得在地理上相近的移动设备可以形成一个小型的无线网络。如果处于该网络的某个用户发出了一项服务请求，那么该网络内任何可以提供相应服务的移动设备都可能成为其服务的提供者。同时，由于用户所请求服务的复杂性，在执行过程中原服务请求可能被分解为多个子服务来完成，这一系列子服务通过某些方式组成一个服务组合，并且每个子服务可以由不同的设备提供。将服务分解为多个子服务，既可以减少服务的复杂性以获得更好的解决方案，同时某些子服务的并行执行可以减少服务的执行时间。此外由于不同的设备完成同一个服务所需的时间并不一致，这就导致了选取不同的设备完成服务的总时间会不一致。

在移动Ad Hoc网络中，由于设备的移动性，设备之间随时可能失去连接，此时服务组合就会失效。目前关于在动态环境中服务组合的可靠性研究，大部分关注于现有的服务组合被打断之后如何进行未完成的服务，而本文的目标是为服务组合中包含的原子服务搜寻合适的服务提供者时进行失效风险估计，使得服务组合能够具有较高的可靠性。根据参考文献[1～3]的结论，在移动网络环境中可对移动的服务节点进行聚类，得出两个服务节点处于某个地理范围内的时间范围。根据这一结论，本文对服务节点之间的移动性进行了分析，并针对服务节点的移动性可能使两个节点失去连接从而引起服务组合中断的现象，提出了失效风险模型，此模型设计出3种用于确定服务组合中原子服务的服务提供者节点的算法，最后实现枚举算法，与本文提出的算法进行对比。

文章的主要贡献如下：

·针对Ad Hoc网络环境的特点，结合动态预测技术结果，提出一种失效风险模型以描述服务组合失效的可能；

·设计并实现了3种算法为服务组合中的每个原子服务分配合适的服务提供者；

·在动态预测技术准确的情况下，实现对比算法，得到具有最高可靠性的组合方案，以此对比分析本文提出的算法的可行性以及必要性。

2 相关工作

随着服务组合技术的不断发展，它的应用领域越来越广。然而，由于影响服务组合可靠性的因素多种多样，在静态环境中，网络负载、带宽等都会影响其可靠性；在动态环境中，服务节点的移动性是影响服务组合可靠性的重要因素。因此，服务组合的可靠性问题一直是服务组合技术面临的一大重要课题。目前，学术界对于服务组合可靠性问题有着大量的研究。针对移动网络内节点动态的性质，参考文献[4]提出了一个框架，该框架包含服务路由和网络路由两部分，用于组合和发现服务，以此实现最小化服务的打断次数。同样地，面对动态网络环境中服务组合所面临的若干问题，参考文献[5]针对如何使用户动态地按需使用网络中的各种服务这一问题，提出一种虚拟服务模型，并在此基础上定义了虚拟服务的组合运算，给出了动态服务查找的算法。另外还介绍了支持虚拟服务透明组合的P2P服务组合原型系统，并在实验基础上对虚拟服务及其支撑引擎进行了客观评价。实验表明，其所述虚拟服务及支撑引擎能使面向服务的应用较好地适应动态网络环境下的服务变化，使用户能够透明地按需使用各种资源。参考文献[6]从服务节点的动态性有利于服务组合优化的观点出发，利用运动辅助优化算法，通过减少冗余的跳转次数来减少网络开销，从而改善服务组合的性能。参考文献[7]针对服务组合失败概率大等问题提出了Web服务随机QoS指标的度量方法和自适应QoS管理体系结构，利用随机离散系统唯一的动态控制方法——马尔可夫决策过程（MDP），设计出了随机QoS感知的可靠的Web服务组合。为了提高Web服务组合的可靠性，参考文献[8]使用Web服务业务过程执行语言（WS-BPEL）来支持成功的服务组合。该技术通过WS-BPEL的诞生动态替换服务，可以有效地阻止由于意外发生的服务错误导致的服务组合失效，从而提高服务组合的可靠性。

此外，参考文献[9～13]从不同角度使用不同的方法来解决服务组合的可靠性问题。参考文献[9]提出一种基于语言的框架来解释服务模型和组合逻辑；参考文献[10]设计一种服务组合重组的方法来保证服务组合的全局QoS；参考文献[11]研究如何使用优化链路状态路由协议维持移动网络中服务的质量；参考文献[12]提出一种支持动态地选择Web服务的模型，从而使得服务组合能很好地使用网络环境的变化；参考文献[13]提出一种Web服务可靠性的阶段模型，描述Web服务在服务发布、服务发现、服务组合等各个阶段的失效过程，并构建不同阶段的可靠性模型进行可靠性预测。

上述研究工作从不同方面对服务组合的相关技术进行了分析与探讨，从而为本文的研究提供了良好的基础。然而对这些研究工作分析后可发现，大部分研究工作主要关注于如何在服务组合执行过程中进行动态的服务提供者调整或者在服务组合被打断之后如何进行服务组合的重组。而对于综合考虑服务节点的移动性，并根据服务节点的移动性进行可靠性预测等方面的相关研究仍未充分开展。针对这一情况，本文利用服务节点移动预测技术，对服务节点的移动性进行了分析与考虑，并在此基础之上进行服务组合可靠性模型设计以及寻找相应的服务提供者的算法设计。

3 问题定义以及模型设计

本文目标是在动态网络环境中为服务请求寻找可靠性较高的服务组合方案。考虑图1的服务请求示例。

pi表示移动设备的编号，{si,i=0,1,…}表示移动设备可以提供的服务的集合。在一个网络中存在着多个移动设备，每个设备可以提供若干个服务。如果此时网络中的某个用户发出一个服务请求request，假定request的内容为s1→{s2,s4}→s3，其中s2和s4并行执行。服务请求用户会将该请求发送给所有它可以连接到的移动设备。接到请求后，每个移动设备反馈给请求用户可以提供的服务列表。请求用户根据列表信息以及位置预测的信息确定请求中每个服务的提供者。

对于图1所示的服务请求示例，箭头所示的路径表示一种服务组合提供者方案，箭头上标明的数字表示该条路径的执行顺序，箭头的指向表示数据流的方向。箭头所示路径的含义为由p2提供服务s1，p5和 p7分别提供服务 s2和 s4，p3提供服务 s3。

由图1可知，对于同一个服务请求，可以有多种服务提供者方案。由于执行服务的过程中设备处于移动状态，因此会出现服务执行中断的情况。另外不同的移动设备完成同一服务的时间有所不同，会直接导致整个服务请求的完成时间有所不同。本文针对上述由于设备移动导致的服务中断问题，提出了相应的衡量服务组合方案可靠性的标准，并提出相应的数学模型以及算法，以确定服务请求的服务提供者分配方案。

3.1 基本概念

在动态网络中，影响服务组合可靠性的因素多种多样，本文只针对在动态网络中服务节点的移动性对服务组合的可靠性的影响。为方便阐述，本节定义了一些常用概念。

定义1 （原子服务）在网络中不可再分的，可以完成某项相对简单任务的服务称为原子服务，表示为si（i为服务编号）。

定义2（服务节点）位于移动网络范围内的无线移动设备，表示为Ni（i为设备在网络中的编号）。每个服务节点可以提供多个原子服务，用SNi表示服务节点Ni可以提供的原子服务的集合，SNi={(sk,tki)|k∈N+}，其中tki表示Ni完成服务sk所需的时间，不同的服务节点完成相同服务所需的时间不同。

定义3 （服务请求者）在网络中发出服务请求RS的服务节点，即网络中的某一个服务节点，若服务节点Ni发出请求，则服务请求者表示为Nri。

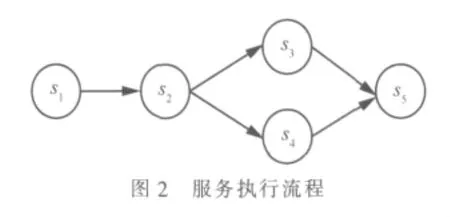
定义4 （服务执行流程图）本文定义的服务执行流程图是由一系列原子服务通过串行或并行的顺序组合而成的有向无环图。每个服务执行流程图对应一个服务请求RS。例如，图2所示是由5个原子服务组合而成的一个服务执行流程，圆圈表示原子服务，箭头表示服务的执行顺序。由s1指向s2表示先执行s1再执行s2，是串行结构；由s2出发有两个箭头分别指向s3和s4，表示s3和s4同时执行，是并行结构，并且只能由不同的服务节点提供。用表示服务执行流程图。

定义5 （服务提供者）在网络中提供服务的服务节点，对于编号为i的服务节点表示为pi。

定义6（服务组合方案）每个服务组合方案对应一个服务请求RS（一个服务请求有多个服务组合方案可以完成），用 S C 表示，S，二元组(si,pj)表示由服务提供者 pj提供原子服务si。

本文考虑无线移动网络环境中的动态性，主要是指携带无线设备的个体的移动性，这种移动性导致了网络内任意两个服务节点在地理上的距离不断变化。由于无线信号极大地受到距离的影响，因此两个服务节点能够保持连接的时间受到了限制。鉴于上述特点，本文做了如下定义用于模拟网络节点的动态性。

定义7（服务节点的相对动态时期）对于处于网络内的任意两个服务节点Ni和Nj，用Tij=[aij,bij]表示这两个节点之间的动态性。即在Tij时间范围内两个节点之间的连接随时可能断开，连接不稳定。在时刻aij之前连接稳定，不受动态性影响，而在时刻bij之后一定会断开连接。

3.2 问题模型定义

由于无线移动网络环境的动态性，使得网络中的任意两个服务节点在某一时刻可能失去连接，导致服务组合的中断。本文旨在为处于无线移动网络环境中的服务请求寻找具有较高可靠性的服务组合方案。给定一个服务请求RS，经过分析得到了完成该服务请求对应的服务执行流程图。根据已知的服务执行流程图，为图中的每个原子服务寻找合适的提供者，并使得所得到的方案具有较高的可靠性即为本文的目标。

根据网络内每个服务节点的Mlist，即可为Gers中的每个原子服务寻找合适的服务提供者。由于服务节点之间的动态性，最终所得的方案存在着失效的可能，因此本文力求在服务组合执行之前进行可靠性分析，使得得出的方案具有较高的可靠性。

对于每一个服务请求RS，根据其他所有服务节点返回的匹配结果列表Mlist设计具有较高可靠性的服务组合方案为本文的目标。本文所考虑的服务组合的可靠性并不是传统意义上的服务组合的服务质量、匹配程度以及容错性等特性，而是针对无线移动网络环境中，由于服务节点的移动性所引起的服务组合中断的可能性。

根据3.1节问题模型中的定义可知，由于每个服务提供者完成原子服务的时间不一样，因此不同的服务组合方案所需的执行时间也不一样。对此本文做出如下定义。

定义8 （服务组合长度）一个服务组合的长度定义为串行的原子服务的数目个数加上并行结构的数目，如图2的服务组合长度为4。

定义9 （服务组合方案完成时间）一个服务组合方案SC所需的完成时间为CT=∑tik(si,pk)∈SC，tik表示服务提供者pk完成原子服务si所需的时间，并行结构中选取最大执行时间作为该并行结构包含的所有原子服务的执行时间。

根据定义7可知，在网络中任意两个服务节点在某一时间范围内可能连接也可能断开。假设服务节点Nrj在某一时刻发出一个服务请求RS，其中的一个服务组合方案中包含了(si,pk)，即由服务提供者pk来提供si，那么如果在si执行过程中Nk和Nrj失去连接，则si被迫中断，服务组合方案失效。

对于某个原子服务si，如果可以找到这样一个服务提供者pk，它与服务请求者保持连接的最后时刻晚于si执行的完成时间，则si可以顺利完成。但是，由于服务节点的频繁移动，为一个SC包含的每个原子服务寻找这样的服务提供者几乎是不可能的，只能寻找具有最小被打断性可能的组合。

定义10 （超时风险系数）对应于服务节点Nrk发出的服务请求PS的一个服务组合方案SC，用rij表示其中的每个元素(si,pj)承担的超时风险系数，即在si还没有执行结束的时候pj和Nrk进入相对动态时期，此时完成服务需要承担一定风险。rij的定义如下：

其中，stij为开始执行服务 si的时刻，ctij为完成si的时刻。stij>ajk,ctij≤bjk表示如果在进入动态期后才开始执行服务，则承担的超时风险系数为100%。当服务的完成时间超出动态期的最晚时间，服务一定会失败，此时不需要考虑超时风险。

3.3 失效风险系数模型

基于上述动态模拟及概念的定义，本文定义了如下失效风险系数模型用于为中的每个原子服务寻找合适的服务提供者，以使得整个服务组合方案具有较高的可靠性。在此，为描述服务组合方案的可靠性，本文做了如下定义。

定义12 （失效风险系数）基于超时风险系数以及不稳定性的定义，用rpij表示由服务提供者pj提供单个原子服务si的失效风险系数如下：

整个服务组合方案的失效风险系数如下：

本文使用风险系数来描述一个服务组合方案的可靠性，规定失效风险系数越小，则其可靠性越高。已知网络内任意两个服务节点的相对移动性和每个服务节点对于特定的Mlist，根据上述定义的风险系数模型以及3.2节中的定义，即可为求得具有较高可靠性的服务组合方案，用 Result表示方案结果，Result={(si,pj)|si∈Ge,rp}，rp 表示方案整体的失效风险值，(si,pj)表示由pj提供原子服务si。

4 基于风险系数模型的可靠性方案设计

假设网络中共有m个服务节点。对于一个包含n个原子服务节点的，若每个原子服务平均有k个服务提供者，那么对于每个都有kn种服务组合方案。若每次都对kn个服务组合方案进行风险系数的计算，然后求得具有最小风险系数的方案是非常耗时的。对此，本文基于第3节提出的失效风险系数模型，提出以下3种算法来解决求解具有较小风险系数的服务组合方案的问题。

假设服务请求者Nr0在进入网络后的st时刻发出一个服务请求，得到中包含 n个原子服务为 s1，s2,…,sn。为每个原子服务分配一个执行顺序编号，用ei表示si的执行顺序，其中属于同一并行结构的服务具有相同的执行顺序编号。已知网络中的其他服务节点均已返回匹配结果列表Mlist，根据Mlist，可以得出每个原子服务的服务提供者集合，用Pi表示服务si的服务提供者集合，Pi={pj|j∈N+}；用Sj表示服务提供者pj可以提供的属于的原子服务集合，Sj={si|si∈}。

4.1 单步枚举算法

单步枚举算法（SsE算法）的主要思想是考虑单个步骤中服务的数量并不会太多，访问一个步骤内所有的执行方案不会大幅增加执行时间。该算法可以取得每个步骤的最优结果，从而使得整体结果具有较高的可靠性。SsE算法的伪代码如图3所示。

在该算法中，每次确定一个执行步骤中的原子服务的执行方案，得到一个执行步骤中的失效风险系数，将每次遍历得到的风险系数相加，即得到整个服务组合方案的失效风险系数总和，确定服务组合方案的可靠性。由于每个执行步骤中包含的原子服务数目远远小于一个服务请求中包含的所有原子服务数目，所以即使存在枚举所有执行方案的可能，也只是局部枚举，对算法的时间复杂度影响并不大，该算法的平均时间复杂度为O(nm)，其中n为中原子服务的数目，m为网络中服务提供者数目。

4.2 最大连续性及最长执行时间算法

最大连续性及最长执行时间（BC-LET）算法的主要思想如下。

从执行顺序编号最小的且未分配服务提供者的原子服务开始，计算每个服务提供者pj能够连续提供的原子服务数目（对于并行的原子服务，选择其中具有最大失效风险系数的原子服务），得到每个服务提供者pj一次连续能够提供的原子服务的集合spj；选择能够提供最多原子服务的服务提供者，并将所有被选择的原子服务视为一个服务，连续执行不可断开。若有多个服务提供者可以提供相同数目的原子服务，则根据失效风险值最小原则选择。BC-LET算法的伪代码如图5所示。

该算法所选择的服务组合方案的整体失效风险系数为每一次选择的服务提供者的失效风险总和，平均执行时间复杂度为O(nm)。

4.3 最晚相对动态期算法

最晚相对动态期（LUTR）算法主要利用已知的服务提供者之间动态信息，在寻找过程中优先选择相对于服务请求者最晚进入动态期的服务节点，然后将该服务节点可以提供的服务标记为已分配服务提供者，在剩余未分配服务提供者的服务中继续按照上述原则进行选择。若在一次选择中有多个服务节点具有相同的进入动态期时间，则优先选择最早进入网络的服务节点，其次选择具有最晚失效时间的服务节点。

由于不同的服务节点完成相同的服务所需时间不同，先执行的服务的执行时间会直接影响后继服务的开始执行时间，因此当有服务还未确定服务提供者时，其后继的所有服务的开始时间都只是一个估计值，这会影响选择的过程。因此该算法在进行一次分配之后，再进行一次调整，对现有分配方案进行调整，调整过程中直接替换不符合条件的服务提供者，按照最小失效风险值进行替换。LUTR算法伪代码如图6所示。

LUTR算法中调用的调整算法adjust_best(i,j,k,pro)需要对服务执行流程图中的每个原子服务进行一次检查，首先判断为其分配的服务提供者能否满足时间等要求，不满足则进行服务替换，否则不做任何修改。adjust_best(i,j,k,pro)算法伪代码如图7所示。

4.4 对比算法

假设位置预测不干扰计算结果的条件下，本文将利用枚举法对服务组合的所有可执行方案进行失效风险比例的计算，进而将本文提出的3种算法得到的结果与枚举出的最优方案的结果进行比较，以此证明本文提出的算法在有效改进时间复杂度的情况下依然可以保证结果的可靠性。比较从3方面进行：算法所得失效风险比例值的比较；由于本文提出的算法会出现无解的情况，本文将计算在一定的实验次数中在枚举情况下有解而本文算法无解的次数，以此来证明算法的可行性；比较本文提出的算法与枚举算法的时间消耗。

5 实验

本文实验主要研究了服务组合的复杂性对算法结果及执行时间的影响，同时在相同的数据集上实现了对比算法用于对比本文算法的可行性。服务组合的复杂性主要是指服务组合的长度以及服务组合的并行度P，定义并行度P=n/L，其中n为服务组合中原子服务数量。本文实验对于两个服务节点之间的不稳定性函数使用均匀分布表示，即服务节点 Ni和 Nj在 t(aij≤t≤bij)时刻的不稳定性

实验数据集的基本设置如下：在[0，T]时间段，网络中总共有50个服务节点进入或离去，每个服务节点在网络中停留的时间不超过T。本文设定T=100个时间单位，另外设定共有50个原子服务可供选择，每个服务节点可以提供5～10个原子服务，完成每个原子服务的时间为3～20个时间单位。

5.1 服务组合长度L的影响

固定参数 P=2，然后改变 L 的值分别为 2、3、4、5、6、7，每种情况进行50次实验取平均值，得到如图8所示的实验结果。根据图8的结果可知，当服务组合长度较小时，4种算法的结果比较接近。而随着服务组合长度增加，3种算法以及对比算法得出的失效风险值均有所增加，增加幅度也都不断变大。总体而言，SsE算法与最优结果的值最接近。而BC-LET算法和LUTR算法由于在求解过程中有较多的估计运算，导致结果有所偏差，但是在值不超过5的情况下，其结果与SsE算法和最优结果同样比较接近，证明其在长度较短的情况下同样适用。

5.2 服务组合并行度P的影响

考虑现实情况下服务组合的并行度不会很大，因此本文实验只考虑P=1、P=2、P=3的情况。固定参数L=4，进行实验，所得结果如图9所示。分析图9可知，P值对SsE算法、LUTR算法和对比算法的影响趋势不稳定，原因在于3种算法对于每个并行结构的失效风险取值只取其中最大的一个，并不是总和，因此趋势不稳定。而BC-LET算法是从服务提供者的角度来计算失效风险，因此随着并行度的增加，其所得到的值也不断增加。

结合图8和图9可知，3种算法的结果与最优结果有所差距，但是整体而言结果较优，尤其是SsE算法。之所以不能采用枚举算法得到最优结果，是因为时间上不允许。

5.3 完成时间对比

本文对4种算法进行了完成时间的分析，表1、表2、表3分别是不同L值和P值下4种算法的执行时间，表格中的**表示无法执行完成，未得到时间结果。

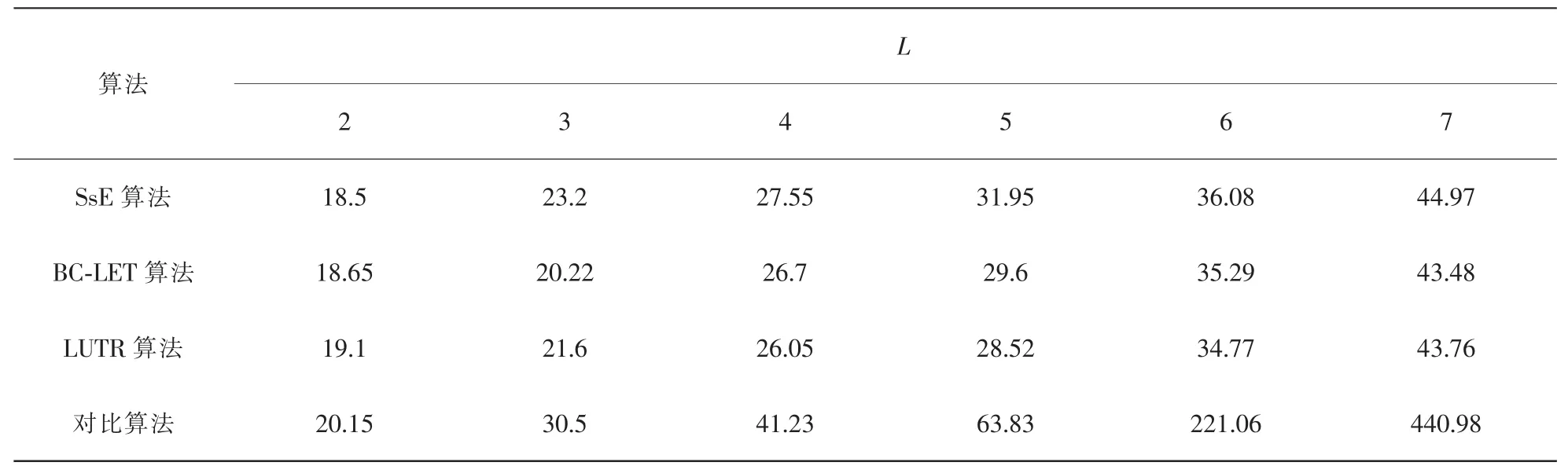
表1 P=1时不同L值下每种算法的执行时间（ms）

表2 P=2时不同L值下每种算法的执行时间（ms）

从表1～表3的结果可以看出，本文提出的算法基本都能在0.1 s时间内得出结果。而对比算法只有在服务组合的P=1的情况下或者P=2的少数情况下可行，一旦服务组合复杂度变高，则其执行时间是不可估量的。而且，本文实验使用的数据集是采用少量数据的，现实情况中若每个原子服务的服务提供者数量过多，则对比算法根本不可能实现。

此外，由于本文提出的3种算法都没有遍历所有可能的组合方案，存在着原本可以找到匹配服务组合的请求却未能得到结果的可能，本文用错判概率wp来表示这种可能性其中fr表示未得到匹配组合方案的服务请求次数，sr表示存在匹配组合方案的服务请求次数。为了验证本文提出的算法的可行性，分别对每种算法进行720次运算得到fr值，并执行对比算法得到sr值。实验结果见表4。由表4的数据可以得出sr=712，因此SsE算法、BC-LET算法和LUTR算法的wp值分别是3.79%、5.05%、3.23%，可见本文提出的算法的错判率并不会影响算法整体的可行性。

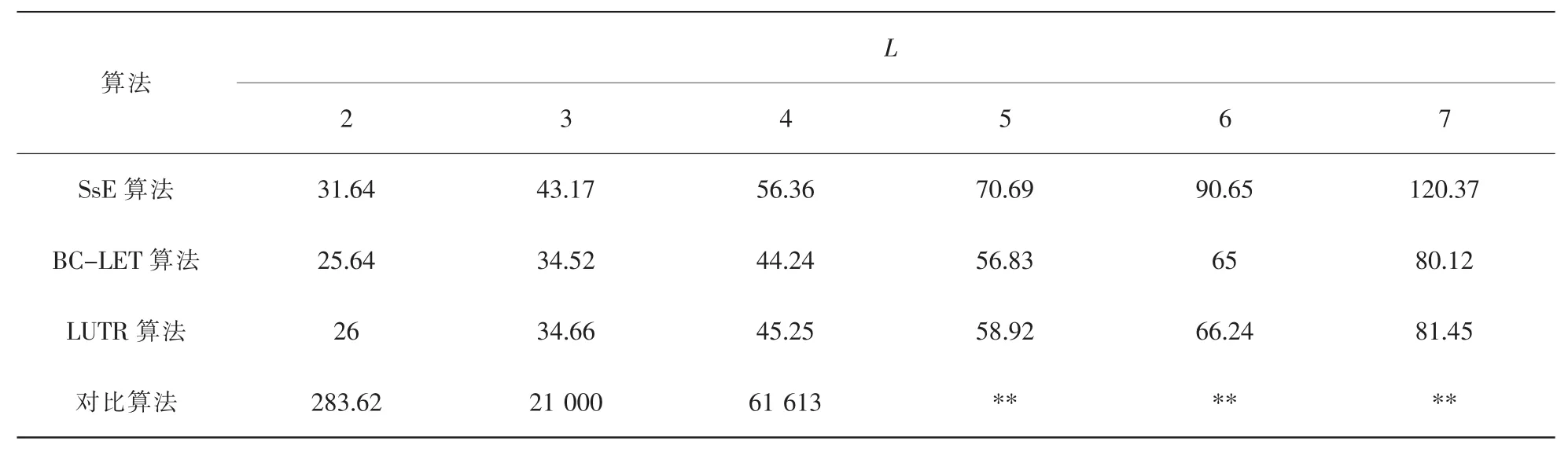
表3 P=3时不同L值下每种算法的执行时间（ms）

表4 720次执行中每种算法没有得到结果的次数

6 结束语

本文主要研究了在移动Ad Hoc网络中服务组合的可靠性问题，提出了一个数学模型以及3种算法以解决此问题，并通过实验证明提出的算法的可行性。

本文所考虑的服务组合目前只包含了并行和串行两种结构，并没有考虑到现实情况下一个任务可以由不同的服务完成的选择情况，未来将在这方面进行研究。此外，文章所用的数据集虽然描述了网络中服务节点的移动性，但也与实际情况会有所差距，采集实际数据进行研究也将是未来研究工作的一方面。

1 McDonald B,Znati F.A mobility based framework for adaptive clustering in wireless ad hoc networks.IEEE Journal on Selected Areas in Communications,1999,17(8):1466～1487

2 Yutaka Yanagisawa.Predictive indexing for position data of moving objects in the real world.Transactions on Computer and Science,2009(1):77～94

3 Gao Y J,Zheng B H.Continuous obstructed nearest neighbor queries in spatial databases.SIGMOD’09,2009:577～589

4 Jiang S S,Xue Y,Douglas C,et al.Minimum disruption service composition and recovery over mobile ad hoc networks.Mobile and Ubiquitous Systems:Networking&Services,2007:1～8

5 Li G,Ma X J,Han Y B.Transparent service composition in dynamic network environments.Chinese Journal of Computers,2007,30(4):579～587

6 Ibrahima K T,Yang Y,Zhen Q M,et al.Low redundant hop-countsforservice composition optimization in dynamic network.IEEE International Conference on Cloud and Service Computing,Guilin,China,2011:26～31

7 Fan X Q,Jiang C J,Wang J L,et al.Random-QoS-aware reliable web service composition.Journal of Software,2009,20(3):546～56

8 KIM J P,Hong J E.Dynamic service replacement to improve composite service reliability.International Conference on Secure Software Integration and Reliability Improvement, IEEE Computer Society,Washington D C,USA,2011:182～188

9 Wang Y,Sharad Singhal,Hamid Reza Motahari-Nezhad.A language-based framework for analyzing service representation models and service composition approaches.IEEE International Conference on E-Business Engineering,Shanghai,China,2010:222～229

10 Sherry X Sun,Zhao J.A decomposition-based approach for service composition with global QoS guarantees.Information Sciences,2012(5):138～153

11 Ge Y,Thomas Kunz,Louise Lamont.Quality of service routing in ad hoc networks using OLSR.Proceedings of the 36th Hawaii International Conference on System Sciences,Hawaii,2003

12 Xu D M,Zhao H,Zhang H G.Dynamic web service composition selection strategy for reliability.Computer Science,2011,38(8):53～59

13 Xie C L,Li B X,Wang X F,et al.A staged model for web services reliability.Journal of Southeast University,2012,42(1):40～44