数学娱乐(十一)—幻方与线性代数

耿 济

(海南大学，海南海口570228)

本文是数学娱乐［1～10］的续作，应用线性代数方法探讨幻方.

1 洛书与线性方程组

中国古书《易经》中的洛书是世界上最古老的幻方，现在用矩阵表示

其中，1，3，5，7，9原来用小白点的数目表示，把奇数代表阳;2，4，6，8 原来用小黑点的数目表示，把偶数代表阴，这与阴阳学说有关.考古学上发现的“奇字”是6位数字，正是《易经》卦象的起源［8］.由此可见，洛书在《易经》中具有特殊和重要的地位.

洛书在数学上具有2个基本性质.

加法性质 每行、每列、左右对角线上3个数字和等于15.

乘法性质 每行3个数字相乘，3个乘积相加等于每列3个数字相乘，3个乘积相加［3］.

洛书与线性方程组有下述关系.

设 x1，x2，x3，…，x9是 1，2，3，…，9 的某种排列，下列矩阵为

要求A中每行、每列、左右对角线上相加等于15，试求x1，x2，x3，…，x9正整数解.

这一问题含有9个未知量，从要求中知道有8个方程，实际上还有9个未知量相加等于45，总共有9个方程，这是一个9个未知量、9个方程的线性方程组求解的问题.

线性代数在理论上提出判别线性方程组有没有解的方法，应用上提出使用计算机求解的方法，因此，近代科技上应用广泛.

已知线性方程组

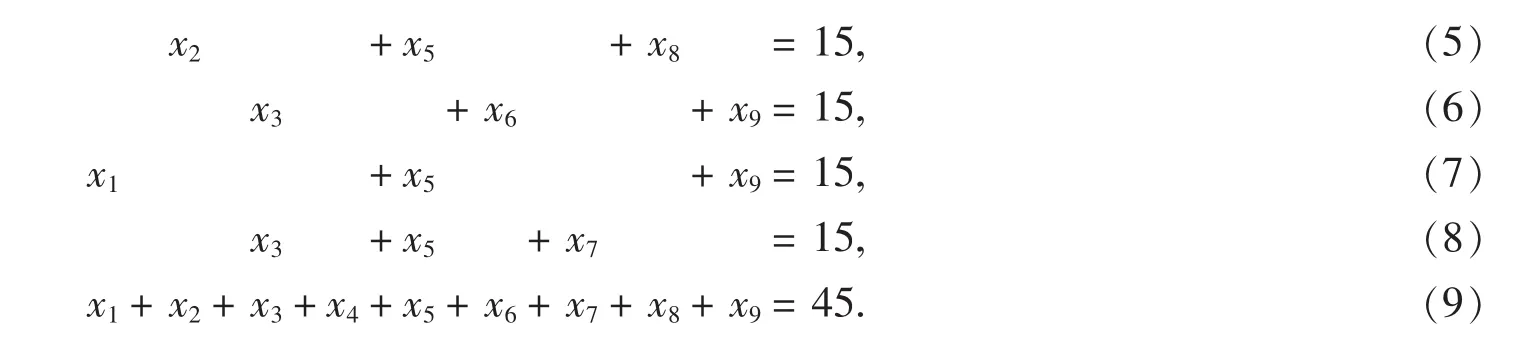
求解时，首先写出线性方程组未知量的系数以及常数项的矩阵B，称B为增广矩阵;其次对B施行初等行变换，即下述3种变换:

1)B 中对调 i，j两行，记作 ri↔rj;

2)以数k≠0乘B中i行，记作kri;

3)把B中j行的k倍加到i行上，记作ri+krj.

最后经过一系列的矩阵初等行变换，把B变成标准形式

由此得出等价的线性方程组，即得通解的结果.

从已知线性方程组得到

经过一系列的矩阵初等行变换得到标准形式

由此得出等价的线性方程组

现在采用参数u=x8，v=x9，立即得到原方程组的通解

这里参数 u，v，既具有任意性，可以多种选取;又具有约束性，因为 u=x8，v=x9，x1，x2，…，x8，x9是 1，2，3，…，8，9 的某种排列，参数 u，v 的全部解为(1，6)，(1，8)，(3，4)，(3，8)，(7，2)，(7，6)，(9，2)，(9，4).此时原线性方程组共有8组解，也就是说3阶幻方有8个，洛书是其中的1个，通过2种不同的旋转正好产生8个不同的幻方.

附注 式(21)是x5=5，与参数无关，从式(2)、(5)、(7)、(8)相加，减去式(9)除3得出式(21).标准形式中有2行全为零，因为式(1)，(2)，(3)相加就是式(9)，又式(4)，(5)，(6)相加也是式(9)，说明式(1)～(9)的9个方程中有2个是“多余”的方程，即可以删去.此外式(14)即式(21)，x5=5，代入式(5)和(7)分别得出式(11)和(10)即式(18)和(17)，还有式(3)就是式(16)，也是式(23).由此可见，线性方程组在计算上还可以得到很大的简化.

2 Nasik幻方与行列式

Nasik幻方是4阶幻方中最有趣的一类幻方，它比通常的4阶幻方要求条件更高.具体地说，如果下述4阶幻方是一个Nasik幻方，由自然1～16为元素构成的矩阵

每行4个元素和等于34，即a1+a2+a3+a4=b1+b2+b3+b4=c1+c2+c3+c4=d1+d2+d3+d4=34，每列4个元素和等于34，即a1+b1+c1+d1=a2+b2+c2+d2=a3+b3+c3+d3=a4+b4+c4+d4=34，还有左、右对角线上4个元素和等于34，即a1+b2+c3+d4=a4+b3+c2+d1=34，除以上一般4阶幻方具有的条件外，还有左、右泛(折)对角线上4个元素和等于34，即a2+b3+c4+d1=a3+b4+c1+d2=a4+b1+c2+d3=34以及a1+b4+c3+d2=a2+b1+c4+d3=a3+b2+c1+d4=34.由此可见，一般4阶幻方要求10个等式成立，而Nasik幻方要求16个等式成立，这就是Nasik幻方的定义.

2009年笔者［4］以线性方程组为工具获得等价Nasik幻方的新定义，即要求每行、每列4个元素和等于34，还有 a1+c3=a2+c4=a3+c1=a4+c2=b1+d3=b2+d4=b3+d1=b4+d2=17.

Nasik幻方与行列式有下述关系.

定理 Nasik幻方共有384个，任意一个对应的行列式都等于零.

证明 已知Nasik幻方共有384个［4］，现在任取一个Nasik幻方对应的行列式

从等价Nasik幻方的新定义中知道

分别代入第3行、第4行，得到

第3行减1行，第4行减第2行，就有

已知 a1+a2+a3+a4=34，即 a2+a4=34－(a1+a3)，b1+b2+b3+b4=34，即b2+b4=34－(b1+b3)，代入第3行、第4行，又有

从第3行提取公因式17－(a1+a3)，第4行提取公因式17－(b11+b3)，又有

最后由于行列式中第3行、第4行对应的元素相等，所以行列式D=0.

如果举例验证，不妨从历史上著名的3个Nasik幻方［4］中挑选一个

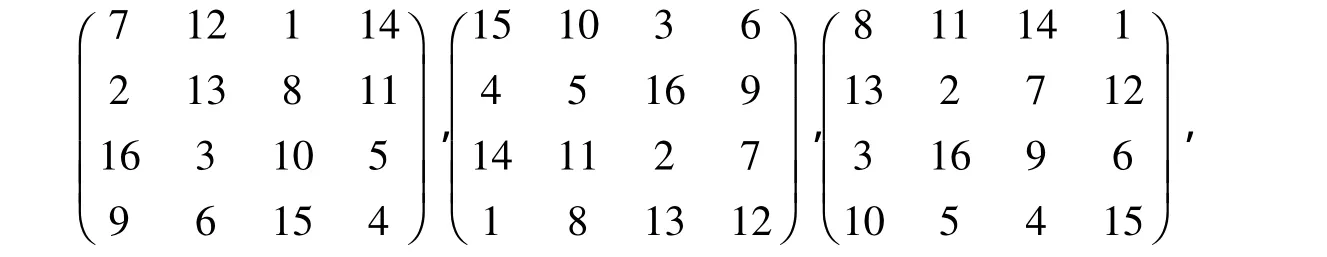
自行加以计算(或者按照文献［4］另作1个Nasik幻方).

3 矩阵乘法新概念及其在幻方上的应用

为了探讨2个任意阶幻方相乘得出新幻方的问题，导出矩阵乘法新概念.

定义 设n阶矩阵

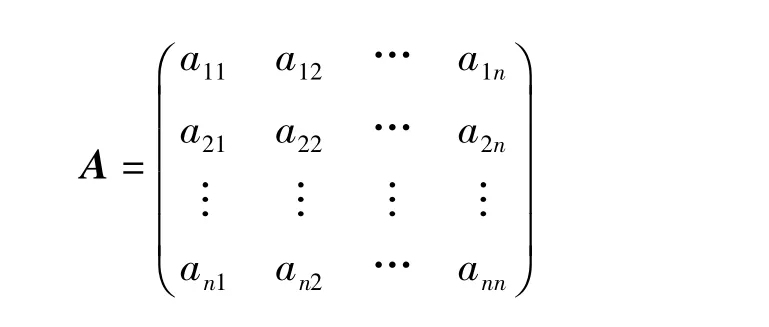
与m阶矩阵

的新乘法用分块矩阵表示为nm阶矩阵

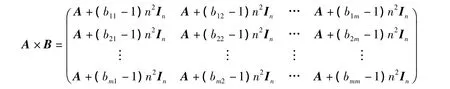
以及

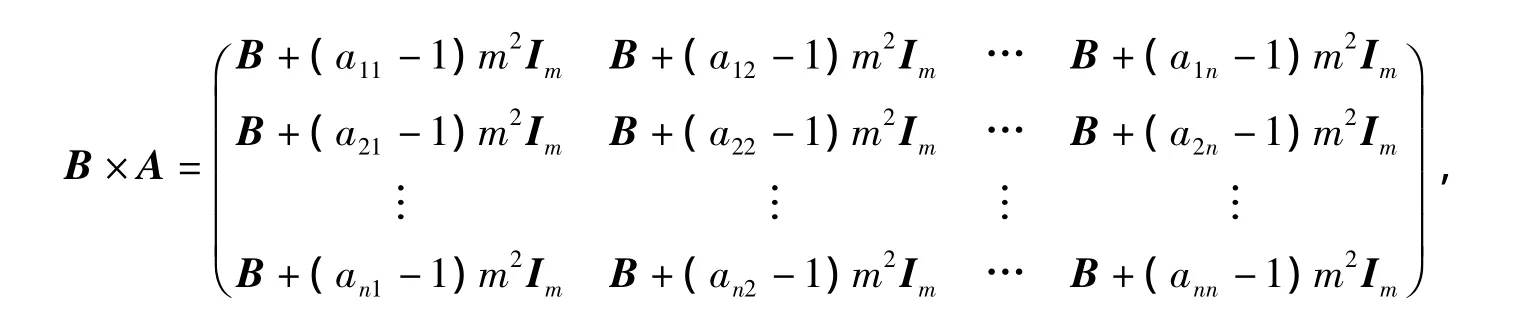
其中In，Im分别表示为n阶、m阶的矩阵，它们所有的元素全部等于1.

例 已知

试求A×B，B×A的乘积.

解

由此可见，A×B≠B×A，即A，B的乘积不满足交换律，对于结合律A×(B×C)=(A×B)×C是成立的(严格的证明从略).

上例实质上是幻方A与幻方B相乘，经过验证A×B与B×A都是幻方，因为每行、每列以及左、右对角线上12个数字和等于870(它们的元素分别是由1～144构成的).

一般而言，获得下述结果.

性质 n阶幻方A与m阶幻方B相乘得到nm阶幻方A×B与B×A.

证明 假设n阶幻方A的第1行的元素为a11，a12，…，a1n，m阶幻方B的第1行的元素为b11，b12，…，b1m时，现在计算A×B中第1行各元素相加，按照A×B的法则得到m(a1+a2+…+an)+(b1+b2+…+bm－m)n2·n，已知 a1+a2+… +an=［(n2+1)n］/2，b1+b2+…bm=［(m2+1)m］/2，代入即得

所以A×B的第1行nm个元素和符合幻方第1行的要求.其余的第2，…，n;n+1，n+2，…，2n;…;n(m－1)+1，n(m －1)+2，…，nm 各行，证法相同.

至于A×B的各列nm个元素和应用上法得到［(n2m2+1)nm］/2，左、右对角线上的nm个元素和也能得到［(n2m2+1)nm］/2，所以A×B是nm阶的幻方.

类似地，证得B×A也是nm阶幻方.

上述性质的重要性就是通过矩阵乘法新概念解决了幻方相乘等于幻方的新结果.由此又导出一些新概念:例如幻方A的自乘，即A的平方，记为A2，就有幻方

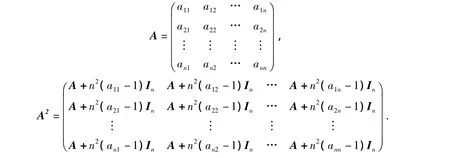
例 试求幻方

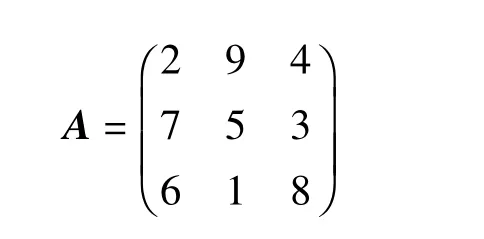
的幻方A2.

解 从已知的3阶幻方A得到9阶幻方

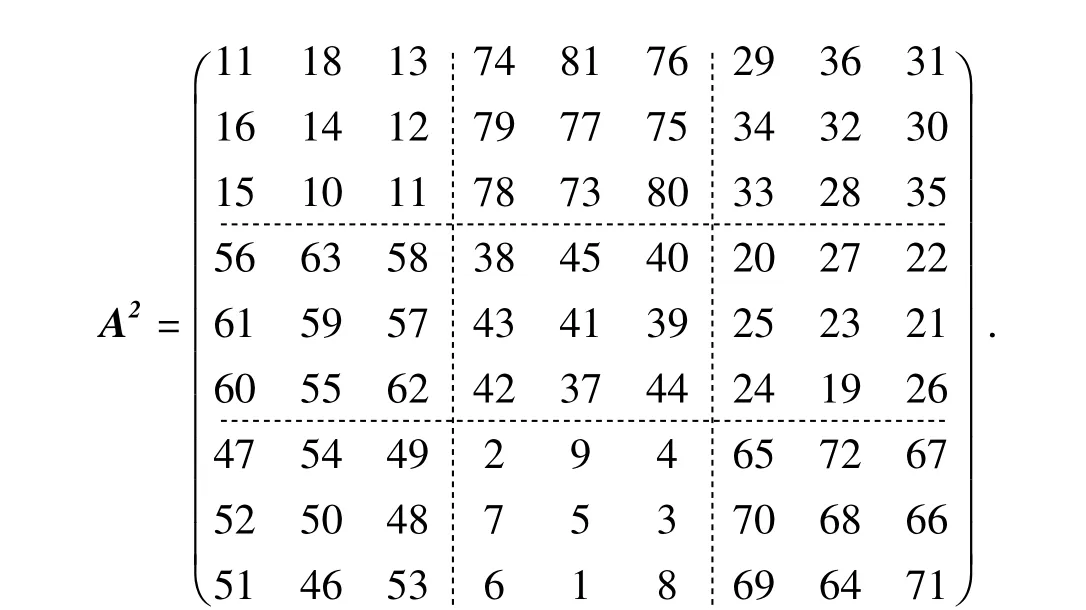
幻方A不仅有A2，还有A3以及An的新幻方，通过幻方乘法出现高阶幻方.

回顾文献［11］王永健指出的:“现在，已排出的最大幻方，是n=105，即包含1052(个)数的方阵，它的幻和N105=578，865，是由美国纽约市普莫勒市的一个13岁少年孙达完成的”.时至今日，这一“世界之最”恐怕早已被打破.本文应用3阶幻方与4阶幻方相乘得出12阶幻方，12阶幻方自乘就是144阶幻方;如果把144阶幻方再与12阶幻方相乘出现一个1 728阶幻方，估计它就是现在的“世界之最”.笔者认为追求幻方的最大阶数意义不大，应该与其他的学科相结合，为幻方的发展提供新的方向.本文将幻方与线性代数相结合，也为线性代数的发展提供新的内容.

［1］职济.数学娱乐(一)——夫妻问题的新证与应用［J］.海南大学学报:自然科学版，2007，25(4):321－324.

［2］耿济.数学娱乐(二)——牙牌问题的新证与推广［J］.海南大学学报:自然科学版，2008，26(3):206－219.

［3］耿济.数学娱乐(三)——洛书定理与应用［J］.海南大学学报:自然科学版，2008，26(4):303 －308.

［4］耿济.数学娱乐(四)——Nasik幻方的性质与构造法［J］.海南大学学报:自然科学版，2009，27(2):107－115.

［5］耿济.数学娱乐(五)——推广Fibonacci数列与幂级和［J］.海南大学学报:自然科学版，2008，27(4):313－319.

［6］耿济.数学娱乐(六)——移棋相间［J］.海南大学学报:自然科学版，2010，28(1):1 －10，14.

［7］耿济.数学娱乐(七)——一个麻将和牌问题［J］.海南大学学报:自然科学版，2010，28(2):93－98.

［8］耿济.数学娱乐(八)——易经卦象的起源与考古发现的奇字［J］.海南大学学报:自然科学版，2011，29(2):99－103.

［9］耿济.数学娱乐(九)——学习《九章算术》的收获［J］.海南大学学报:自然科学版，2011，29(4):297 －304.

［10］耿济.数学娱乐(十)——学习《九章算术》的收获［J］.海南大学学报:自然科学版，2012，30(2):95 －102.

［11］王永健.世界之最·数学分册［M］.南京:江苏人民出版社，1981.