基于聚类分析的分数阶Fourier变换信号分离与检测

邵亚勇,竺小松

(解放军电子工程学院,合肥230037)

1 引 言

宽带信号侦察往往存在多个信号同时到达接收通道的情况,若不同信号分量频带相互重叠,很难准确地检测出各个分量。时频分析为解决这类问题提供了一种很好的途径,其基本思想是设计时间和频率的联合函数,用它同时描述信号在不同时间和频率的能量密度或强度[1]。常用的时频分析方法有短时傅里叶变换(STFT)、Wigner-ville分布(WVD)、小波变换(WT)、分数阶Fourier变换(FRFT)等。STFT窄的观察窗和WT宽度变化的时间窗影响了时频域的分辨率;在非线性时频分布中,WVD对LFM信号具有最好的时频聚集性,但是其变换过程的非线性会受到交叉项的困扰[2]。

FRFT变换首先由Namias V从纯数学的角度提出,之后Almeida L B将其解释为时频平面上的旋转算子并分析了它和Wigner-Vile分布的关系。由于FRFT变换计算非常复杂,直到Ozaktas提出FRFT的两种离散计算方法[3],才使其得以广泛应用于信号处理和光学分析。文献[4]和文献[5]从不同角度应用分数阶Fourier变换进行信号检测和估计,但每次只能检测一个信号,效率较低。本文利用FRFT对宽带信号特别是LFM信号具有很强的能量聚集性,从提高分数阶域的极值搜索和多信号的分离、检测效率着手,在混沌-多步拟牛顿搜索法中引入聚类分析的思想,并采用“CLEAN”的方法,将已检测出的强信号分量消除,减小对弱信号的遮蔽作用,以实现多个频谱混叠信号的快速准确的分离和检测。

2 分数阶Fourier变换的定义及性质

典型的 Fourier变换可以理解为逆时针旋转π/2,实现信号从时域到频域的变换。当旋转角 α以π/2的非整数倍旋转时,假定 α=pπ/2,p为任意实数,可得输入信号x(t)的FRFT定义式为

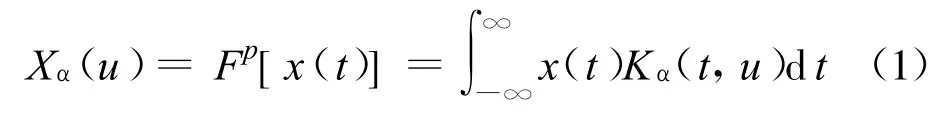
式中,p为FRFT的阶数,Fp[·]为FRFT的算子符号,变换核函数Kα(t,u)为

由式(3)可以看出,信号x(t)由一组权系数为Xα(u)的正交基函数Kα(t,u)所表征。

为方便多分量信号的分离与检测运算,现介绍分数阶Fourier变换的一些基本性质。

(1)线性,满足叠加定理:

(2)旋转相加性:

为减小运算量,本文采用基于FFT的离散FRFT计算方法。由于 x(t)的分数阶Fourier变换为

式中,γ=cotα,β=cscα。若令阶数 p为0.5≤ p≤1.5,函数 ejπγt2x(t)在频域具有带宽 F,令 N=(F)2,由文献[3]可知离散分数阶Fourier变换可表示为

再对分数阶Fourier域上的变量 u取离散值,则上式进一步变为

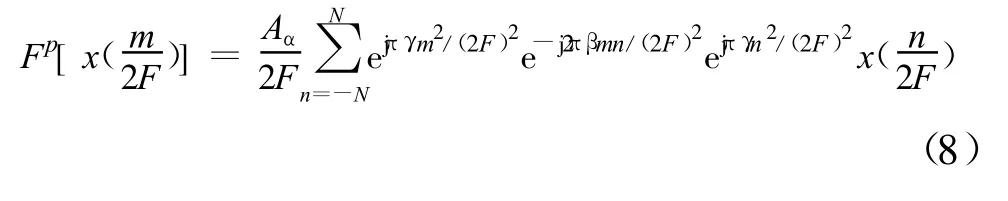
3 多分量信号模型及FRFT域中的遮蔽作用

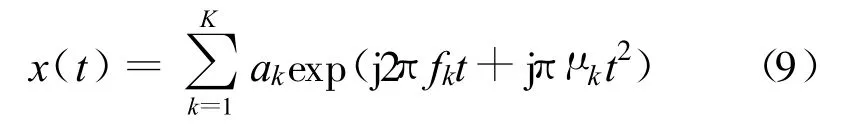
式中,-Δt/2≤t≤Δt/2,ak、fk、μk分别为信号的振幅、初始频率和调制频率,K为信号的个数。单频信号和调幅信号可认为是LMF信号的特例。

在FRFT平面上,LFM信号所对应的冲激函数的位置可以表示为[2]

设多分量信号的表达式以LFM信号为模型:

当在FRFT域中同时检测多个信号分量时,信号之间存在一定的遮蔽作用,文献[6]分析了两信号之间的遮蔽性能,设信号分量 g(t)和 h(t)分别在α0、α1阶FRFT域中实现最佳能量聚集,遮蔽系数的定义为

式中,Ag、μg为g(t)的幅度和调频率,Ah、μh为h(t)的幅度和调频率,Td为采样时间,fs为采样频率。遮蔽系数 εα1体现了分量 g(t)对h(t)的遮蔽作用,其值越小越容易将两信号分离。从式(13)可以看出,在信号幅度和调频率确定的情况下,遮蔽系数εα1与采样时间有关,采样时间越长,遮蔽作用越小。

4 基于混沌-多步拟牛顿混合法和聚类分析相结合的多分量信号的分离与检测

由式(10)可知,对多分量LMF信号做分数阶Fourier变换,每一分量只在FRFT域中特定的位置(αk,uk)上才表现为冲激函数。只需不同分量信号的初始频率和线性调频系数有一个不同,就可将它们分离。首先从p=1阶FRFT着手,滤除强的窄带信号。对接收到的混叠信号进行离散FRFT变换,形成信号能量在参数(α,u)平面上的二维分布。在确定的旋转角α=π/2,按信号强度进行搜索,得到各窄带信号对应的参数 u,通过式(11)计算信号参数,并重构信号。之后通过在变换域 u设计窄带滤波器,或应用重构信号进行对消,去除混叠信号中的窄带信号。

其次对剩余的宽带LFM 信号,在FRFT域(α,u)上采取混沌优化法和多步拟牛顿法(BFGS)相结合的混沌-多步BFGS混合法[7]进行二维搜索。混沌优化法的基本思想就是用类似载波的方法将混沌状态引入到优化变量中,并把混沌运动的遍历范围“放大”到优化变量的取值范围,然后利用混沌变量进行搜索[8]。通过一定的混沌映射关系,产生混沌序列,并比较各序列的目标值,如果在一定步数内目标函数值不发生变化,满足终止条件,作为当前最优值输出。该方法具有较强的全局搜索能力。

拟牛顿法是一种下降搜索方法,在FRFT域二维平面(α,u)内,寻找合适的(α0,u0)使得目标函数达到最小,即 :

而在拟牛顿法基础上发展的多步拟牛顿法[9],充分利用前期迭代所得信息,构造正定对称矩阵,提高了算法的速度和精度。因此将混沌优化算法与多步拟牛顿法相结合的混沌-多步BFGS法,能够保证全局最优解的同时,提高搜索的速率和精度。

由于通常的逐次消去法每次检测一个最大信号,多次对信号求FRFT,进行二维搜索,再逐个滤除最大信号,计算量大、效率低。采用聚类分析的方法,可以一次处理多个能量相近的信号,减少了信号变换的次数,降低了多次变换引起的信号畸变。文献[10]中通过平面截取信号在(α,u)域上的尖峰,引入广度优先搜索邻居的聚类算法,以期获得每个LMF对应的尖峰位置,实现多个较强信号的检测与参数估计。

本文将混沌-多步BFGS法和广度优先搜索邻居聚类法相结合,通过逐次相消从强到弱,进行多分量混叠信号的分离与检测,具体处理步骤如下所述。

4.1 应用混沌-多步BFGS混合法搜索FRFT域最大值

多步拟牛顿法虽然搜索精度高、速度快,但是其是一种局部搜索法,受初始值影响较大。而将混沌优化算法与多步拟牛顿法相结合,能够实现全局收敛性和收敛速率快的目的,避免在步进搜索中,步长因子选择不当造成收敛速率与检测精度不协调的问题。图1所示为混沌-多步BFGS混合法的流程图。

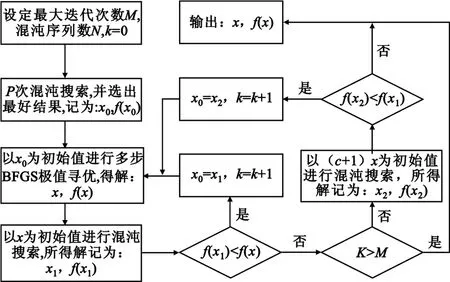
图1 混沌-多步BFGS混合法流程图[7]Fig.1 Flowchart of chaos-multi-step BFGS method

4.2 信号尖峰的聚类分析

FRFT域中信号尖峰包含了信号的所有信息,只要搜索出信号尖峰在FRFT域中所处的位置即可检测出对应信号参数。选择一个合适的平面,对平面(α,u)上的信号尖峰进行切割,以切割的信号尖峰作为聚类输入集。设(α0,u0)为FRFT域最大值对应的位置,选择合理的高度因子 m,以为切割平面的高度作初次切割,在保证切割的信号数最多情况下,又不至于切割到噪声或干扰,提高每次切割的效率。令 T=,设行数和列数分别为 r、l,T 的矩阵元素为Tij,1≤i≤r,1≤j≤l。利用平面切割,求出聚类输入集Y为

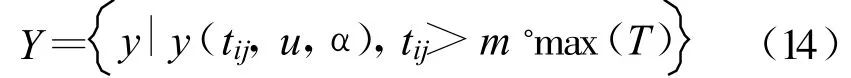
以相异度矩阵作为两个对象之间近似性的量化表示。对于给定对象 x以及任意对象xi,r为距离参数,找出在聚类分析输入集Y中的直接邻居和间接邻居。如果符合设定的类门限参数 λ,则将它们归为一类,完成一次聚类。在完成聚类处理之后,搜索各类的局部极大值,把对应的尖峰坐标(uk,αk)代入式(11)求出LFM信号的参数值。

4.3 逐次消去检测到的强信号分量

在信号消去的方法中,一种是根据已检测出的LFM信号参数进行信号重构,通过自适应的方法将重构信号与原混叠信号对消,消除强分量,但这种方法在信号检测与对消过程中易受到误差的影响。另一种方法是在变换域u上作带阻滤波。对原混叠多分量信号作旋转角度αk变换:

式中,Sαk(u)为对应于角度 αk有冲激函数的信号,Wαk(u)代表其他信号分量作旋转角度为 αk的变换。再在u域内对尖峰进行遮蔽处理:

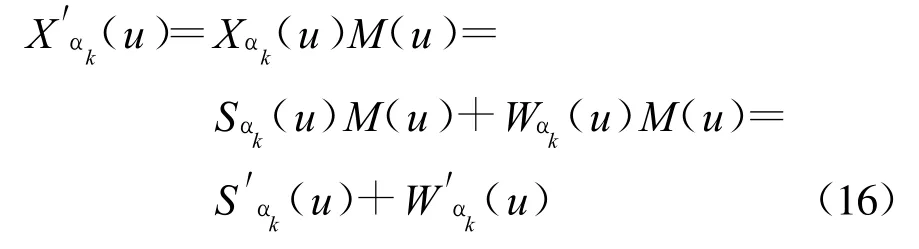
M(u)为中心频率为 u的带阻滤波器,适当选择其带宽,保证既能滤除强信号分量,又对其他信号不造成较大损伤。

4.4 滤除强信号后的时域恢复

对遮蔽处理后的信号作逆FRFT变换,得到经过一次聚类分析和信号消除后的剩余信号分量。对剩余信号进行放大,然后重复以上流程,直到满足特定门限,使剩余成分中不再含有所需信号分量。

5 仿真与分析

假设接收信号中含有5个信号分量,其中两个窄带信号分别为

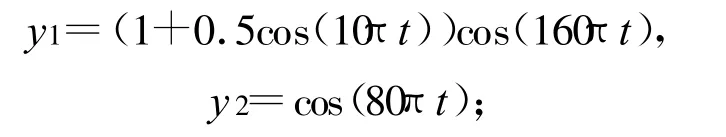
其余3个宽带LFM分量,振幅分别为 a3=1.2、a4=1、a5=1,初始频率分别为 f3=40 Hz、f4=75 Hz、f5=95 Hz,调频斜率分别为 k3=9Hz/s、k4=12 Hz/s、k5=5 Hz/s。噪声为加性零均值高斯白噪声,信噪比为6 dB。图2所示为各信号分量的频谱图,图3为混合信号的频谱图。

图2 各信号分量的频谱图Fig.2 The spectrum of the signal components

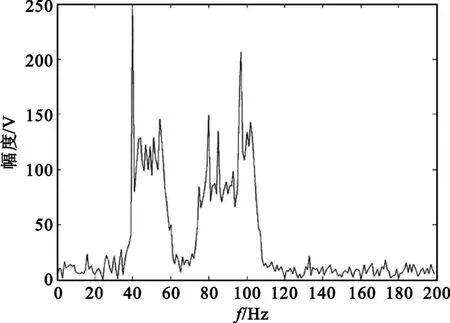
图3 混合信号的频谱图Fig.3 The spectrum of mixed-signal

由图2和图3可知,接收的多信号分量之间在频谱上相互重叠,通过频域滤波的方法,不能进行分离及检测各分量的参数。先做FRFT,首先检测出p=1上的余弦信号和调幅信号,之后将检测出的信号从混叠信号中消除。消去窄带余弦和调幅信号前后多分量信号的FRFT变换的频谱图分别如图4和图5所示。

图4 原混叠信号的FRFT幅值图Fig.4 The FRFT magnitude diagram of original signal

应用混沌-多步拟牛顿法检测出最大信号的FRFT域位置为( α, u)=(3.086 1,2.218 8),在进行聚类分析之前,设定各参数的值为:平面切割的高度因子m=0.7,距离参数r=0.02,类门限参数 λ=0.95。信号尖峰的第一次聚类结果如图6所示。

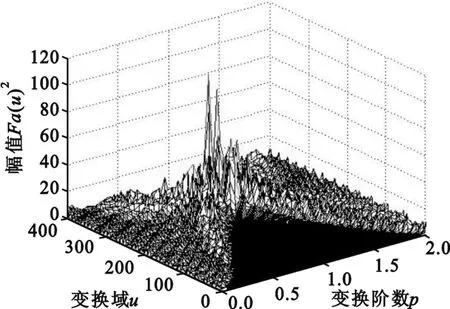
图5 消去窄带信号后的FRFT幅值图Fig.5 FRFT magnitude after eliminating narrow-band signals

图6 信号尖峰的第一次聚类结果Fig.6 The first signal peak clustering result

在进行尖峰聚类时,若存在的多个信号分量,弱分量的能量小于强分量的0.7倍时,只进行一次聚类,将会导致弱信号不能检测出来,此时应将检测出的强信号分量在混叠信号中消除,减小对弱信号分量的遮蔽作用。然后再应用混沌-多步拟牛顿法检测出剩余信号中的最大信号,使用聚类分析,得到多个能量相近信号,直到所有信号分量都被检测出来。

信号y3、y4、y5分别在各自的最佳旋转角和对应u值的尖峰图如图7所示。

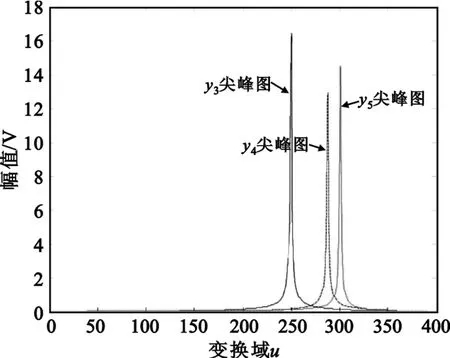
图7 y3、y4、y5最佳旋转角处FRFT幅值图Fig.7 The FRFT magnitude of y3,y4,y5in best rotation angle

6 结 论

本文研究了将混沌-多步拟牛顿法和聚类分析综合应用于分数阶Fourier变换进行频谱重叠信号的分离与检测,改变了之前研究中单纯提高搜索速率或单纯应用聚类分析的方法,通过理论分析和仿真验证,本方法与其他方法相比,能够在保证检测精度的前提下提高检测效率。文中只考虑了单频、调幅和线性调频3种信号混叠的检测,对于混叠信号中含有更多种调制信号的分离与检测,将是我们下一步研究的重点。

[1]张贤达,保铮.非平稳信号分析与处理[M].北京:国防工业出版社,2001.ZHANG Xian-da,BAO Zhen.Non-stationary signal analysis and processing[M].Beijing:National Defense Industry Press,2001.(in Chinese)

[2]齐林,陶然,周思永,等.基于分数阶Fourier变换的多分量LFM信号的检测和参数估计[J].中国科学(E辑),2003,33(8):749-759.QI Lin,TAO Ran,ZHOU Si-yong,et al.Detection and parameter estimation ofmulticomponent LFM signal based on the fractional Fourier transform[J].Science in China(Series E),2003,33(8):749-759.(in Chinese)

[3]OzaktasHM,Kutay O,Kutay M A,et al.Digital comp utation of the fractional Fourier transform[J].IEEE Transacti ons on Signal Processing,1996,44(9):2141-2150.

[4]GUO Qing,LI Yanjun,WANG Changhong.A new method of detecting multi-component LFM signals based on blind signal processing[J].Journal of Computers,2011,16(9):1976-1982.

[5]Zhang Xinhui,Liu Lianfu,Cai Jingye,et al.A pre-estimation algorithm for LFM signal based on simplified fractional Fourier transform[J].Journal of Information&Computational Science,2011,8(4):645-652.

[6]邓兵,陶然,曲长文.分数阶Fourier域中多分量chirp信号的遮蔽分析[J].电子学报,2007,35(6):1094-1098.DENG Bing,TAO Ran,QU Chang-wen.Analysis of the shading between multi-component chirp signals in the fractional Fourier domain[J].Acta Electronica Sinica,2007,35(6):1094-1098.(in Chinese)

[7]卫红凯,王平波,蔡志明,等.分数阶Fourier变换极值搜索算法研究[J].电子学报,2010,38(12):2949-2952.WEI Hong-kai,WANG Ping-bo,CAI Zhi-ming,et al.Study of algorithm for extremum seeking in the fractional Fourier transform[J].Acta Electronica Sinica,2010,38(12):2949-2952.(in Chinese)

[8]李兵,蒋慰孙.混沌优化方法及其应用[J].控制理论与应用,1997,14(4):613-615.LI Bing,JIANG Wei-song.Chaos optimization method and its application[J].Control Theory and Application,1997,14(4):613-615.(in Chinese)

[9]Ford JA,Moghrabi I A.Multi-step quasi-Newton methods for optimization[J].Journal of Computational and Applied Math ematics,1994,50(1):305-323.

[10]徐会法,刘锋,张鑫.分数阶Fourier强弱LFM 信号检测与参数估计[J].信号处理,2011,27(7):1063-1068.XU Hui-fa,LIU Feng,ZHANG Xin.Detection and parameter estimation of strong and weak LFM[J].Signal Processing,2011,27(7):1063-1068.(in Chinese)