两种空化模型计算二维水翼空化流动研究

刘 艳， 赵 鹏 飞， 王 晓 放

(1.大连理工大学 能源与动力学院，辽宁 大连 116024；2.大连理工大学 船舶工程学院，辽宁 大连 116024)

0 引 言

空化现象常发生在高速旋转运行的水利机械中，如各种泵、螺旋桨及高速艇水翼.当流场内某处的局部压力低于液体工作温度所对应的汽化压力时，该处液体就会汽化，接着生成气泡，气泡生长直至溃灭，这种现象称为空化现象.该过程涉及相变、质量传输、可压缩性以及流动非定常[1]，因此，空化是一种非常复杂的流动现象，对水利机械的工作性能会产生很大的影响.

传统上研究空化的方法是模型试验.模型试验需要有空化水洞.该设施投资大，周期长.近年来，随着计算流体力学的发展，数值研究空化现象因经济性好、周期短和不受设备限制而受到了研究者们越来越多的关注.空化研究属于多相流计算范畴.在多相流理论中，气相或液相的质量分数或体积分数通过组分方程或代数方法获得.如果使用组分方程，那么不同相之间的流体质量传递通过方程的源项加以考虑.绝大多数空化流动计算中都视工质为单一混合介质，这便是混合多相流模型中混合的含义.

空化流动计算的关键是确定汽(气)、液相之间质量交换量的数学模型.Kubota等[2～4]及Zwart等[5]先后提出了不同的空化模型.这些模型都是基于气泡动力学Rayleigh－Plesset方程推导而来且都获得了不同程度的应用.商业软件FLUENT 6.2中使用Singhal完全空化模型(FCM)，ANSYS CFX 11采用的是Zwart－Gerber－Belamri(Z－G－B)空化模型.Huang等[6]应用完全空化模型[4]对某 NACA66(MOD)水翼在不同攻角时的定常空化形态进行了研究.褚学森等[7]应用(完)全空化模型[4]研究了回转体和圆盘空化器的自然空化流动，给出了不同气核质量分数和湍流参数对空化流动的影响结果.郝宗瑞等[8]对8°攻角的NACA0015水翼进行了非定常二维空化流场的结构和流动特性研究.Kang等[9]数值模拟了直径为200mm的四叶轴流泵的三维空化流动.刘登成等[10]对直径为227mm的INSEAN E779A四叶模型桨的空化流动进行了研究.上述这些计算都是借助FLUENT完成的且获得了令人满意的结果.韩宝玉等[11]借助CFX，应用Z－G－B空化模型模拟了某NACA66水翼的定常和非定常空化流动，并对原Z－G－B空化模型中部分经验系数进行了修改，修改系数后的Z－G－B空化模型的计算结果与试验值吻合较好.

由以上可以看出，文献中大多使用单一空化模型研究空化流动问题.为了比较Singhal等[4]的全空化模型和Z－G－B空化模型的可靠性和计算精度，本文选取二维NACA66翼型进行空化流动计算，并且在空化数较大的情况下进行验证(此种情况下可认为流动为稳定的空化流动)，其中全空化模型借助于 FLUENT 6.2软件实现，Z－G－B空化模型借助于ANSYS CFX 11实现.

1 数值模拟方法

1.1 控制方程

将水和汽(气)的混合物视为不可压流体.流动的控制方程包括质量守恒方程、动量守恒方程和组分方程.在不计及体积力时，直角坐标系下定常不可压流体的雷诺时均的 Navier－Stokes(RANS)方程组可表示为如下形式:

式中:i，j＝1，2，1、2分别代表x和y方向(二维)；U、p分别代表时均速度和静压力；ρm和μm分别表示混合物的密度和动力黏度；τij表示雷诺应力，需要通过湍流模型近似求得.式(3)表示的是混合物中气相的输运方程，其中αv表示气相体积分数，m·＋e和m·－c分别表示单位时间单位体积内气体的产生项和凝结项.如果使用液相输运方程，相应的体积分数和源项分别为液相的体积分数和净质量变化值.

本文计算选用的湍流模型为标准k－ε模型(湍动能k及其扩散率ε的输运方程可参阅文献[12])及壁面函数.雷诺应力τij的计算公式如下:

其中

式(5)中μt表示湍流黏度.混合物的密度ρm由下式计算:

式中:下标v、l和g分别表示气相、液相和不凝结气体，f代表质量分数.如果忽略不凝结气体的影响，式中的fg取为0.体积分数与质量分数间的关系为αv＝fvρm／ρv.如前所述，不同的空化模型，相间质量传递的计算方式不同.

1.2 空化模型

1.2.1 完全空化模型 Singhal等[4]提出的完全空化模型是基于气泡动力学Rayleigh－Plesset方程，气、液两相质量守恒方程和相关物理假设推导而来的，同时考虑了湍流和不凝结气体的影响.气、液两相的质量变化计算式表达如下:

其中

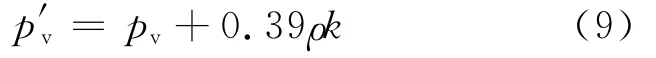
上述表达式中pv代表饱和蒸汽压；k为湍动能；S为表面张力系数；Ce、Cc为模型常数，分别取为0.02和0.01(值得一提的是，当对方程(7)和(8)

进行量纲分析时，发现方程两边的量纲不匹配.文献[1]中也指出了这个问题.将方程(7)和(8)中的用k表示可以满足量纲条件.FLUENT中使用的仍然是原模型.此问题有待进一步研究).

1.2.2 Z－G－B空化模型 Z－G－B[5]空化模型是在忽略气泡表面张力和二阶导数项的情况下，由Rayleigh－Plesset方程得到如下的相间质量传递计算公式:

式中:Rb代表气泡半径；rnuc代表成核区的体积分数；Fvap和Fcond分别为Z－G－B空化模型的经验蒸发系数和凝结系数.各参数取值为Rb＝1μm，rnuc＝5×10－4，Fvap＝50，Fcond＝0.01.

相对于全空化模型，Z－G－B空化模型推导过程比较简单，模型中也没有考虑不凝结气体的影响，但公式中经验常数较多.这些经验常数如果选取得不合适，可能会对结果产生影响.

1.3 数值方法

1.3.1 离散格式 FLUENT 6.2中，提供了不同精度的离散格式.本计算中，对流项选用二阶迎风格式，压力项选用二阶中心差分，气相输运方程选用三阶精度的QUICK格式.使用ANSYS CFX 11计算时，各控制方程均选用高精度的离散格式，即High Resolution格式，它采用一个混合因子来自动调节该区域中采用的差分格式，在变量梯度变化比较小的区域使用一阶迎风格式，在变量梯度比较大的区域使用接近二阶迎风格式.该格式可以较好地平衡计算的稳定性和精度.

1.3.2 计算区域及边界条件 本文算例取自文献[13]中的NACA66水翼.翼型的弦长C为150 mm，攻角为6.5°，最大厚度比的位置距叶片前缘45%，其值为12%，最大拱度比的位置距叶片前缘50%，其值为2%.基于弦长和来流速度(5.33 m／s)的雷诺数为8×105.实验段上下表面距离为192mm，翼展长为191mm.

计算采用二维区域.计算域大小为7C×192 mm2.边界条件的设置如图1所示.入口条件为均匀来流(5.33m／s)，出口给定静压.入口处距叶片前缘2C，出口处距叶片前缘5C.网格采用C型结构化网格.计算采用的介质为20℃的水(密度998.2kg／m3，动力黏度0.001 002kg／(m·s))和水蒸 气 (密 度 0.017 31kg／m3，动 力 黏 度0.000 973kg／(m·s))，饱和水的表面张力系数为0.072 361N／m，饱和蒸汽压pv为2 340Pa.

图1 计算域及边界条件示意图Fig.1 Schematic of the computational domain and boundary conditions

2 计算结果与分析

计算中使用的初生空化数和翼型表面静压力系数分别定义如下:

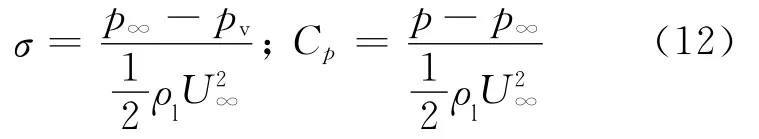
其中U∞为无穷远来流速度；p∞为无穷远处压强，这里取出口压力；p代表翼型表面静压强.

2.1 网格无关性讨论

研究与空化有关的文献发现，绝大多数空化流动计算中都使用高雷诺数湍流模型.作者的试算也发现高雷诺数模型比低雷诺数模型预报的结果要好.这可能是由于空化模型的验证是在高雷诺数湍流模型条件下进行的.基于此，本文湍流模型选用标准的两方程k－ε模型.对于标准的k－ε模型，壁面附近不需要求解ε，即不需要求解湍动能耗散率的输运方程，使用基于壁面速度对数率导出的代数方程获得.使用壁面函数时，要求壁面处第一层网格节点的量纲一壁面距离y＋大于30.FLUENT 6.2和ANSYS CFX 11中使用修正的壁面函数，使得第一层网格节点的量纲一壁面距离y＋大于11即可.

使用FLUENT对无空化流情况进行网格无关性研究.根据经验公式，选取第一层网格高度为4×10－4m，网格伸展比为1.2，叶片周向网格节点数为220，网格节点总数为35 462，此网格作为初始网格.然后将此网格在各个方向上加密1倍，所得的网格作为加密网格(网格节点总数70 924).图2给出了两种网格下叶片表面第一层节点的y＋分布情况，图3给出了吸力面压力系数分布.

图2 无空化流时两种网格下叶片表面的y＋分布Fig.2 Distribution of y＋on the low sides of the hydrofoil for two kinds of grids for a noncavitating flow

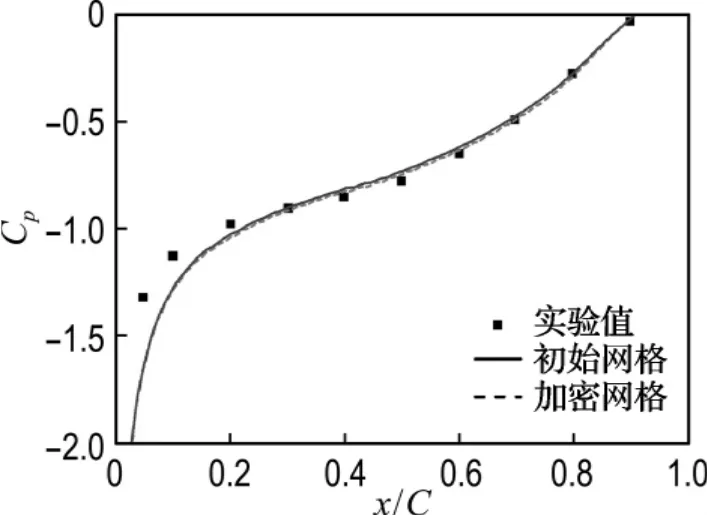
图3 无空化流时两种网格得到的叶片吸力面上压力系数分布Fig.3 Distribution of pressure coefficients on the suction side of the hydrofoil for two kinds of grids for a noncavitating flow

由图2可以看出，粗、细网格下得到的第一层计算节点y＋的平均值分别为40左右和20左右，满足使用壁面函数的要求.由图3可看出，加密网格和初始网格下，吸力面压力系数的计算结果差别不大，均与实验值吻合较好.考虑到计算的经济性，以下的计算采用初始网格即粗网格.

2.2 无空化流时叶剖面压力分布比较

图4比较了无空化流情况下，两种软件得到的NACA66翼型吸力面上的压力系数分布情况.由图4可知当x／C＜0.2，两种软件预报的Cp均小于实验值；当x／C＞0.2后，计算值与实验值均吻合较好.尽管两种软件使用的壁面函数和数值方法不同，但无空化流时计算结果基本一致.

图4 NACA66翼型无空化流时吸力面压力系数分布比较Fig.4 Comparison of the pressure coefficients on the suction side of NACA66hydrofoil at noncavitating flow

2.3 空化流动计算结果与分析

空化计算时，发现不同空化模型中经验系数的大小对结果有一定影响.由于文献[13]中没有给出实验条件下不凝结气体质量分数等参数，计算中需要选取合适的经验系数.计算入口的湍流度取0.5%(通常水洞实验时的来流湍流度为0.5%[14])，出口压力值根据空化数确定.2.3.1 完全空化模型中不凝结气体质量分数对计算结果的影响 在空化数为1.41情况下，考察3种不凝结气体质量分数情况，即fg＝5×10－6、fg＝1×10－6和fg＝5×10－7，从中确定合适的fg.图5给出了吸力面上的压力系数分布情况.由图5可以看到，随着不凝结气体质量分数的减小，空化区长度减小，这与文献[15]的结论一致.从本文的计算结果看，当fg＝1×10－6或fg＝5×10－7时，压力系数分布曲线与实验值吻合较好.此外，从图5中还可以看出，完全空化模型在空化区末端压力梯度比较大，这和文献[4]计算结果一致.表1给出了空化数为1.34和1.41时不同fg情况下，计算得到的升力系数和阻力系数结果.

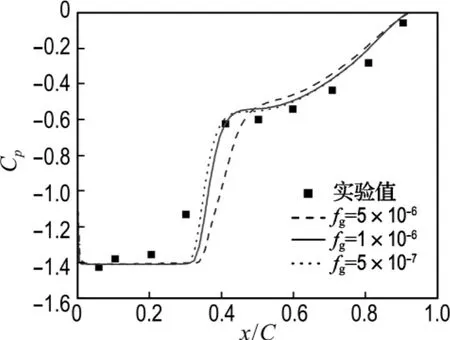
图5 3种不同fg时叶片吸力面上压力系数分布情况比较(σ＝1.41)Fig.5 Comparison of the pressure coefficients on the suction side of the hydrofoil for three kinds of fgwithσ＝1.41

观察表1可以看出随着不凝结气体质量分数的减小，升力系数减小，阻力系数也同时减小.这是空化区为低压区造成的.随着不凝结气体质量分数的减小，空化区即低压区长度减小，吸力面上非空化区即压力恢复区长度增大，这样翼型上下两表面间的压差减小，因而升、阻力系数减小.由此看出完全空化模型中不凝结气体质量分数对结果有一定的影响.当fg＝1×10－6时计算误差相对较小.这与FLUENT 6.2中默认值fg＝1.5×10－5不一致.fg＝1.5×10－5是常温下水中气体的质量分数.空化水洞实验时，因为要抽真空，所以水中气体含量会小些.文献[4]中取fg＝1×10－6，因此本文最终选取fg＝1×10－6.

表1 不同fg时升力系数和阻力系数计算结果和误差Tab.1 Calculated lift and drag coefficients and relative errors for different fg

2.3.2 Z－G－B空化模型中不同系数对计算结果的影响 由式(10)和(11)可知 Z－G－B空化模型[5]中有4个经验常数.这些常数经过不同算例验证过，具有一定的通用性，但是根据本文试算和文献[11]结果发现，这些常数值不是最佳值，某些参数如蒸发系数和凝结系数需要调整.本文在计算中，初始气泡半径Rb和成核区的体积分数选用原模型中的值，即Rb＝1×10－6m，rnuc＝5×10－4，其他两个系数进行验证选取.

(1)Z－G－B空化模型中不同蒸发系数对计算结果的影响

以空化数为1.41的工况为例，蒸发系数分别选取50(模型中原始值)、100和200.3个不同蒸发系数时计算得到的吸力面上的压力系数分布情况见图6.由图6可以看出，当Fvap＝50时，数值预报的空化消失过渡区与实验结果有些偏离.随着蒸发系数增大，结果有所改善.表2给出了不同蒸发系数时升力系数和阻力系数的计算结果和误差.由表2可以看出，随着蒸发系数增大，升、阻力系数的绝对值变化不是很大，但由于本身值很小，相对误差变化很大.综合压力分布曲线和升、阻力系数值，以下计算选用Fvap＝100.

图6 不同蒸发系数时叶片吸力面上压力系数分布情况(σ＝1.41)Fig.6 Distribution of pressure coefficients on the suction side of the hydrofoil for differentFvapatσ＝1.41

表2 不同蒸发系数时升、阻力系数计算结果及误差(σ＝1.41)Tab.2 Calculated lift and drag coefficients and relative errors for different Fvap(σ＝1.41)

(2)Z－G－B空化模型中不同凝结系数对计算结果的影响

同样以空化数为1.41的工况为例，凝结系数分别选取0.010 0(Z－G－B空化模型中给定的原始值)、0.005 0和0.002 5进行计算.其他参数选原模型中的值.图7显示的是3种不同凝结系数时吸力面上压力系数分布情况.由图7可以看出，当Fcond＝0.010 0时，预报的过渡区与实验结果有些偏离.随着凝结系数的减小，完全空化区变短，空化过渡区变长，总的空化区长度增加，压力梯度变小.表3给出了不同凝结系数时升力系数和阻力系数的计算结果和误差.由表3可看出，Fcond＝0.010 0和Fcond＝0.005 0 的 结 果 基 本 一致，Fcond＝0.002 5时误差较大.综合压力分布曲线和升、阻力系数值，以下计算选用Fcond＝0.005 0.

图7 不同凝结系数时叶片吸力面上压力系数分布情况(σ＝1.41)Fig.7 Distribution of pressure coefficients on the suction side of the hydrofoil for differentFcondatσ＝1.41

综合以上结果，使用Z－G－B空化模型计算时，经验系数选取如下:成核区的体积分数rnuc＝5×10－4，气泡半径Rb＝1×10－6m，蒸发系数Fvap＝100及凝结系数Fcond＝0.005 0.

2.3.3 两种空化模型计算结果比较 图8显示了3种空化数，即σ＝1.41、1.34和1.30情况下，完全空化(fg＝1×10－6)和 Z－G－B(Fvap＝100，Fcond＝0.005 0)空化模型得到的吸力面上的压力系数分布情况.由图8可以看出，空化数减小，壁面上空化区长度逐渐增大.每种空化数下，空化开始时流体压力最小(小于汽化压力)，之后一段距离内汽化压力保持不变(此区域长度因空化数不同而不同)，然后压力迅速增大至完全液态区，流体压力再逐渐增大.与实验结果相比，不同空化数时，完全空化模型得到的空化区长度偏大，而ZG－B空化模型得到的空化区长度偏小，但后者空化区末端的压力变化趋势与实验结果更趋一致.两种模型得到的吸力面上的压力分布趋势与实验结果一致.结合流场分析可知，空化区末端的压力变化是受水的回射流影响的.

表3 不同凝结系数时升、阻力系数的计算结果和误差(σ＝1.41)Tab.3 Calculated lift and drag coefficients and relative errors for different Fcond(σ＝1.41)

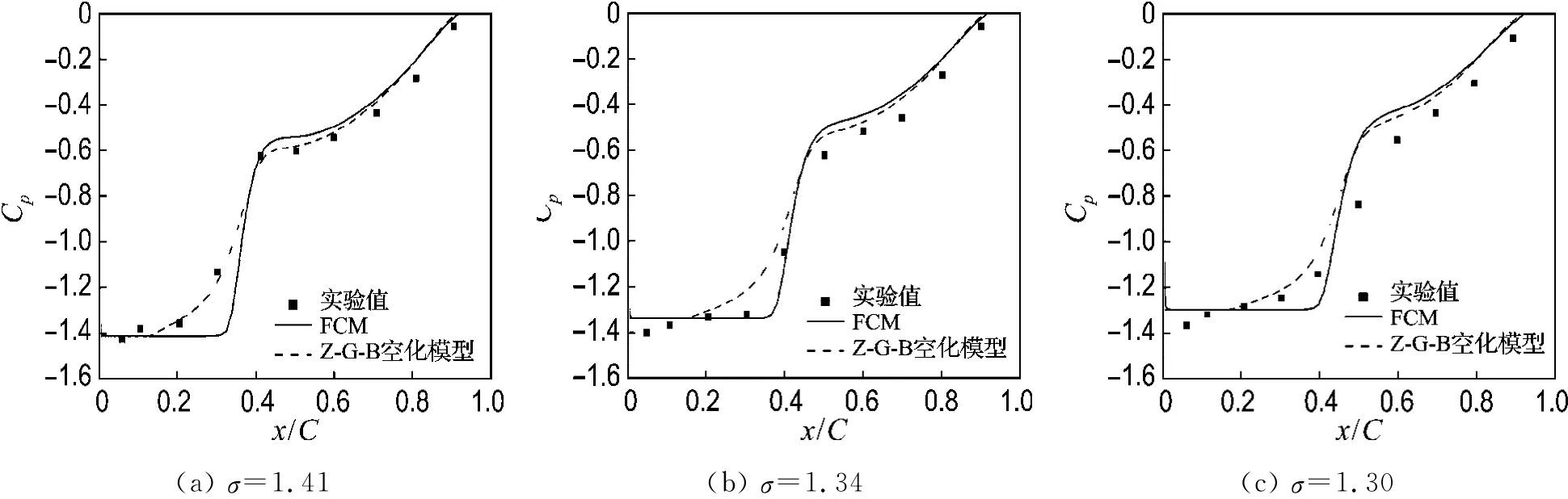
图8 不同空化数时叶片吸力面上的压力系数分布Fig.8 Distribution of pressure coefficients on the suction side of the hydrofoil at different cavitation numbers

图9 给出了不同空化数时两种空化模型得到的水的体积分数分布云图.由图9可以看出，3种空化数下，两种模型都预测出了吸力面前缘附近水的汽化区(水体积分数很小区)即空化区，但两个空化区大小和形状不完全一致.完全空化模型得到的沿壁面空化区长度比Z－G－B空化模型长，与图8压力系数分布情况一致，而Z－G－B空化模型得到的壁面以外的空化区长度比全空化模型长.图10比较了两种模型得到的流线图，可以发现每种空化数下两种空化模型得到的流场中空化区末端都有一个回射流区，但回射流区的大小和形状不一致.Z－G－B空化模型得到的回射流区更细长.由此不难理解图9中Z－G－B空化模型得到的水体积分数分布图上空化末端区较长的原因.

图9 不同空化数时两种空化模型得到的水的体积分数云图Fig.9 Water volume fraction contours for two cavitation models at different cavitation numbers

图10 不同空化数时两种空化模型得到的流线Fig.10 Streamlines obtained from two cavitation models at different cavitation numbers

表4汇总了3种空化数情况下FCM和Z－GB空化模型得到的升力、阻力及各自分量的计算结果.可得两种模型预报的升力的相对误差均在5%以内.Z－G－B空化模型得到的升力的相对误差比FCM小些，但阻力预报值偏低.阻力由两部分组成.一部分是形状阻力即压力差引起的，另一部分是黏性摩擦力(简称黏性力).由表4可以看出，两种模型预报的黏性力比较接近，但压差引起的阻力有一定差别.说明两种模型预报的压力场不完全一致.观察图8和9可以看出Z－G－B空化模型得到的空化区长度偏小，导致翼型上、下表面间的压力差减小，因而合压力也偏小.

为了进一步比较本文所研究的两种空化模型的表现，本文对文献[5]中的NACA66(MOD)水翼(最大拱度比0.02，最大厚度比0.09)进行了空化流动计算.空化数为0.91.完全空化模型中使用的不凝结系数为1×10－6.Z－G－B模型中成核区的体积分数除了取原值rnuc＝5×10－4以外，还计算了rnuc＝5×10－3的情况.两种情况下Z－G－B空化模型中的Rb、Fvap及Fcond与2.3.2节中相同，分别为1×10－6m、100和0.005 0.图11给出了完全空化模型和Z－G－B空化模型预报的吸力面上压力系数分布.由图11可以看出，两种模型的表现与前面NACA66的一致，即完全空化模型预报的空化区长度比Z－G－B空化模型的大，空化过渡区中Z－G－B模型预报的压力变化比全空化模型小一些.为便于比较，图11中也给出了由原始Z－G－B空化模型得到的结果(图中以原始系数表示).由图11还可以看出，对于Z－G－B空化模型，rnuc＝5×10－3预报的结果比原始值rnuc＝5×10－4的结果与实验值吻合程度好.说明Z－G－B空化模型中的经验系数不应该恒定不变，应该给出一个取值范围，总体说来，完全空化模型和修正的ZG－B空化模型能够给出正确的压力系数分布.

表4 两种空化模型得到的升力和阻力计算结果比较Tab.4 Comparison of lift and drag obtained from two cavitation models

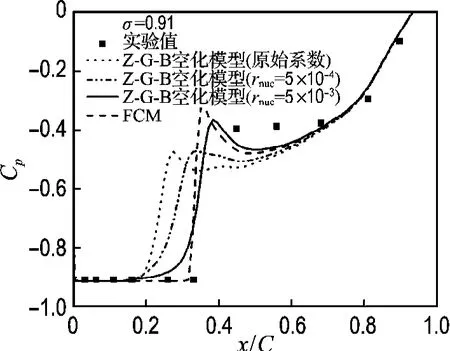
图11 NACA66(MOD)吸力面上压力系数分布比较Fig.11 Comparison of pressure coefficients on the suction side of NACA66(MOD)

3 结 论

(1)FCM和Z－G－B空化模型中的经验系数具有一定的通用性.但在事先无法获得准确信息的情况下，为了得到更好的预报结果，模型中的系数需要调整.

(2)两种空化模型计算空化流动的表现均较好.两种模型得到的吸力面上的静压系数分布和升力系数均与实验值吻合较好.关于阻力系数，ZG－B空化模型预报的空化区较小以及回射流区偏大，导致阻力系数偏小；完全空化模型预测的阻力系数与实验值相差较小，但回射流区偏小.

[1]王献孚.空化泡和超空化泡流动理论及应用[M].北京:国防工业出版社，2009

[2]KUBOTA A，KATO H，YAMAGUCHI H.A new modeling of cavitating flows:A numerical study of unsteady cavitation on a hydrofoil section [J].Journal of Fluid Mechanics，1992，240:59－96

[3]KUNZ R F，BOGER D A，STINEBRING D R，etal.A preconditioned Navier－Stokes method for two－phase flows with application to cavitation prediction [J].Computers and Fluids，2000，29:849－875

[4]SINGHAL A K，ATHAVALE M M，LI H，etal.Mathematical basis and validation of the fullcavitation model [J].Journal of Fluids Engineering，2002，124(3):617－624

[5]ZWART P，GERBER A G，BELAMRI T.A twophase flow model for predicting cavitation dynamics[C]／／International Conference on Multiphase Flow.Yokohama:ICMF，2004

[6]HUANG S，HE M，WANG C，etal.Simulation of cavitating flow around a 2－D hydrofoil[J].Journal of Marine Science and Application，2010，9(1):63－68

[7]褚学森，王 志，颜 开.自然空化流动数值模拟中参数取值影响的研究[J].船舶力学，2007，11(1):32－39

[8]郝宗瑞，王乐勤，吴大转.水翼非定常空化流场的数值模拟[J].浙江大学学报(工学版)，2010，44(5):1043－1048

[9]KANG Can，YANG Min－guan， WU Guang－yan，etal.Cavitation analysis near blade leading edge of an axial－flow pump [C]／／International Conference on Measuring Technology and Mechatronics Automation.Los Alamitos:IEEE Computer Society Press，2009:767－770

[10]刘登成，洪方文，张志荣，等.螺旋桨片状空泡的CFD分析[J].舰船科学技术，2009，31(1):43－47

[11]韩宝玉，熊 鹰，陈双桥.对二维翼空化流动的数值模拟[J].水动力学研究与进展，2009，24(6):740－746

[12]JONES W P，LAUNDERS B E.The prediction of laminarization with a two－equation model of turbulence [J].International Journal of Heat and Mass Transfer，1972，15(2):301－314

[13]LEROUX J B，ASTOLFI J A，BILIARD J Y.An experimental study of unsteady partial cavitation [J].Journal of Fluids Engineering，2004，126(2):94－101

[14]黄继汤.空化与空蚀的原理及应用[M].北京:清华大学出版社，1991

[15]季 斌，罗先武，吴玉林，等.考虑热力学效应的高温水空化模拟[J].清华大学学报(自然科学版)，2010，50(2):262－265