洪水作用下CFRP加固的村镇砖混建筑有限元分析
2012-09-27马兴涛刘永军孙永梅
马兴涛,刘永军,孙永梅
(1.辽宁省水文水资源勘测局沈阳分局,辽宁沈阳110005;2.沈阳建筑大学土木工程学院,辽宁沈阳110168)
0 引 言
我国是洪水灾害多发国家,每年都有大量村镇建筑在洪水中严重损坏甚至倒塌[1-2],如“75.8”河南洪水,倒塌房屋524×104间;“98”长江洪水,倒塌房屋212.85×104间;“03”淮河洪水,倒塌房屋77×104间;2010年7月,吉林省桦甸地区遭受洪灾,倒塌房屋30×104余间。系统深入地研究村镇建筑抗洪性能,对于减少洪水引起的生命财产损失以及建立社会主义新农村具有重要意义。
研究村镇建筑抗洪性能涉及很多内容,本文重点介绍洪水对村镇建筑动水压力的计算方法以及洪水作用下CFRP加固村镇建筑数值模拟方法。
1 洪水对建筑的作用力
1.1 洪水的动水压力计算公式
洪水对建筑的作用力包括浮力、静水压力、动水压力等等,浮力和静水压力比较容易计算,这里重点介绍动水压力的计算公式。一般认为,当洪水的流速大于0.9 m/s时,应该考虑洪水产生的动水压力[3-4]。实验研究表明(见图1),洪水对墙体等构件作用的动水压力在整个迎水面的分布是不均匀的,具体的分布取决于很多因素[4]。本文假设洪水为非粘性不可压缩稳态流,利用动量定理,可以推导出洪水对建筑物迎水面产生的动水压力的计算公式为:
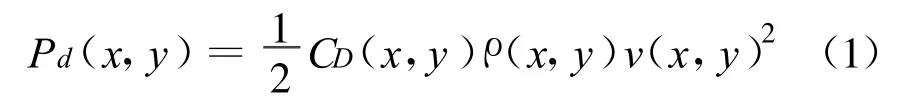
式中:Pd(x,y)为动水压力(N/m2);CD(x,y)为拖拽系数(或绕流阻力系数),取决于迎水面的几何形状、宽度、洪水深度等参数,取值范围为1.0~2.0之间;ρ(x,y)为洪水的密度(kg/m3);v(x,y)为洪水的流速(m/s)。

图1 动水压力及倒塌形态试验[4]
整个迎水面受到的动水压力的合力为:
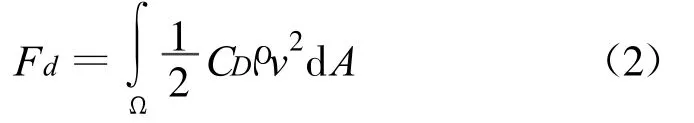
式中:Fd为动水压力的合力;Ω为构件受到洪水冲击部分的表面。
公式(2)是积分形式的动水压力计算公式,不便于实际应用,有必要进行一定的简化。通常,假设迎水面上所有点受到的动水压力为一个与位置无关的常数,拖拽系数根据迎水面的宽深比进行修正,可以得到洪水动水压力合力的近似计算公式。

式中:CA为迎水面平均拖拽系数;ρA为洪水平均密度(kg/m3);vA为迎水面洪水平均流速(m/s);A为迎水面的面积(m2)。
1.2 洪水冲击平面墙体时的拖拽系数
考虑到洪水对村镇建筑的墙体威胁最大,而且村镇建筑的墙体多数都是平面的,所以这里只考虑洪水冲击平面墙体时拖拽系数的数值。根据实验数据的拟合结果,利用迎水面的宽深比(宽度w与水深ds的比值,参见图2)可以确定拖拽系数,具体的关系见表1。
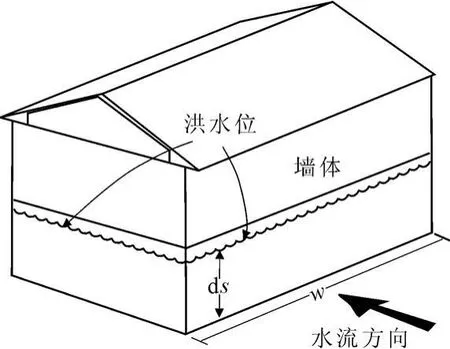
图2 迎水面宽度及洪水深度示意图
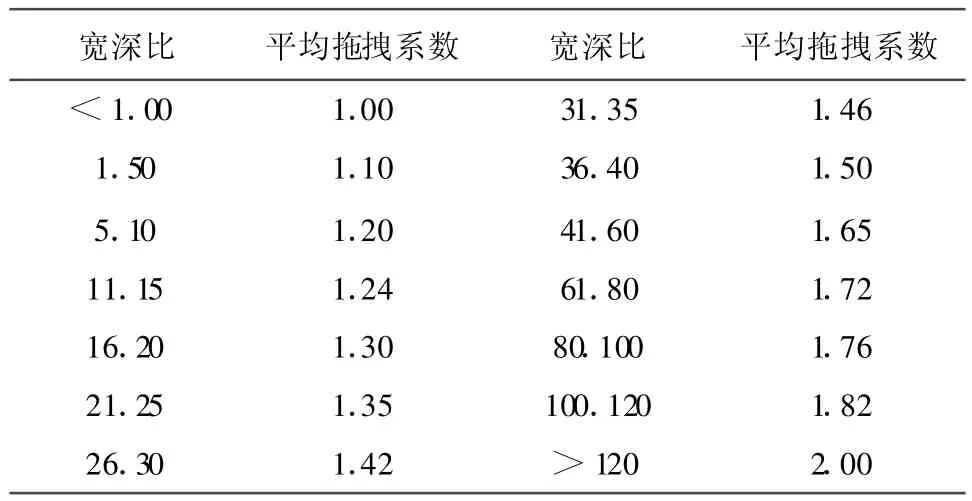
表1 平均拖拽系数与宽深比的关系
当洪水不是垂直作用在墙面,而是与墙面之间有个夹角时,拖拽系数应该适当降低,具体方法是:乘以sinθ,θ为墙表面与洪水流动方向之间的夹角,显然,洪水垂直冲击墙体时,θ=0。另外,当一个建筑与相邻建筑之间的距离小于两个建筑的墙体长度和的一半时,拖拽系数可以提高一个级别。动水压力的合力等于洪水位以下墙体的面积与动水压力的乘积。当墙体上有面积较大的空洞时,计算面积时可以扣除空洞的面积,同时,不考虑空洞对拖拽系数的影响。
2 洪水作用下村镇建筑有限元计算
2.1 基本假定
以东北地区典型的砖混住宅按1∶5的比例建立试验和计算模型,模型的尺寸为180 cm(长)×100 cm(宽)×60 cm(高),中间砌筑两道隔墙。试验结果参阅文献[4],本文主要介绍数值模拟结果。采用大型有限元软件ANSYS进行数值模拟,为了减少计算量,引入如下一些基本假定:(1)墙体与基础之间没有相对位移;(2)洪水的动水压力简化为迎水面上的均布荷载;(3)假设碳纤维布是一种理想弹性材料,始终处于弹性阶段;(4)碳维布与墙体粘结良好,墙体开裂前二者之间没有相对滑移。
2.2 单元类型及破坏准则
采用整体连续模型模拟墙体,将砖和砂浆作为一新的连续墙体材料来考虑,采用Solid65单元模拟墙体,材料参数根据砖和砂浆的材料参数确定。采用Shell63单元模拟碳纤维布。由于Shell63单元厚度可以改变,并且提供了材料的方向角,可以选择碳纤维增强的方向,同时它可以设置为只能承受单向拉伸,非常适合模拟碳纤维布的性能[5-6]。
本文从应力和应变两方面定义构件的破坏准则。应力方面,当墙体单元的主应力超过11.25MPa时,或者剪应力超过0.27 MPa时,认为此单元破坏。从位移方面考虑,当单元的位移超过0.06 m时,本文认为砌体单元的位移过大,将从结构上滑落。
2.3 材料参数
单块砖弹性模量E=1.3×104N/mm2,换算出砖的轴心抗压强度fc=19.5 N/mm2,轴心抗拉强度ft=1.54 N/mm2,泊松比为0.1。砂浆弹性模量E=1×104N/mm2,换算轴心抗压强度fc=5 N/mm2,泊松比0.25[7-8]。CFRP布的材料参数见表2。

表2 碳纤维布的材料参数
2.4 网格划分
未加固的模型称为模型1,用CFRP加固的模型称为模型2,对两者的抗洪性能进行对比。采用有限元软件ANSYS进行数值模拟,墙体采用solid65块体单元模拟,碳纤维布采用shell63壳单元模拟,图3为模型2消隐后的有限元网格。
2.5 约束及荷载
墙体底面的所有结点都被施加约束,去除所有的自由度。动水压力的取值根据模型试验确定[4],屋顶荷载换算成墙体顶面的均布荷载。
3 计算结果对比及分析
3.1 模型1和模型2的应力对比
迎水面墙体受到洪水冲击,应力和位移最大。当流量为1.2 m3/s,水位H=0.6 m时,模型1达到破坏准则,不适于继续承载,宣告破坏。然而,在相同荷载条件下,模型2变形较小,受力状态良好,可继续承受洪水荷载。图4和图5是模型1和模型2中主应力云图。

图3 模型2的有限元网格

图4 模型1第一主应力云图

图5 模型2第一主应力云图
由图4可以看出,模型1在洪水荷载作用下,迎水面上纵横墙交接处砌体墙的拉应力较大,除此之外,迎水面墙体底部应力也比较集中。由图5可以看出,经CFRP加固后,砌体墙迎水面上应力分布比较均匀,受力状态良好。
3.2 模型1和模型2的位移对比
图6和图7是模型1、2的水流方向位移云图。可见,洪水荷载作用下,砌体结构房屋的最大位移出现在迎水面上房屋横墙之间的墙体上,由此可见,合理的横墙间距能有效抵抗洪水荷载的侵袭,可以延缓洪水灾害发生时,村镇砌体住宅发生破坏的时间。当流量为1.2 m3/s,水位H=0.6 m时,模型2迎水面上墙体的最大的位移值为6.349 mm,模型1最大位移达到了10.24 mm,说明CFRP有效提高了墙体刚度,减小了墙体变形。

图6 模型1位移云图

图7 模型2位移云图
图8是模型1和模型2迎水面上最大位移与洪水荷载之间关系曲线,可以看出,墙体位移随着冲击荷载的增加而增大,但并不呈线性变化,在相同洪水荷载作用下,模型1的最大位移均大于模型2的最大位移。
4 结 语
洪水对村镇建筑的墙体具有较大的冲击力,洪水直接冲击是导致村镇建筑倒塌的原因之一。通过模型试验和数值模拟,研究了洪水对村镇建筑作用的动水压力的计算公式及CFRP对村镇砖混建筑的加固效果,得到以下结论:

图8 荷载-位移曲线
(1)文中动水压力的计算公式具有较好的精度,可以用于村镇建筑抗洪性能分析之中。
(2)墙体表面粘贴CFRP加固墙体可以有效提高墙体的抗冲击能力,减小墙体中的应力和位移。
(3)利用ANSYS中的Solid65单元和Shell63单元可以较好地模拟CFRP加固建筑的抗洪性能。
[1]谭徐明,张伟兵,马建明,等.全国区域洪水风险评价与区划图绘制研究[J].中国水利水电科学研究院学报,2004,2(1):50-60.
[2]刘永军,周静海,孟宪宏.村镇建筑抗洪性能评价系统研究与开发[J].土木建筑工程信息技术,2011,3(1):57-62.
[3]Kelman I,Spence R.An overview of flood actions on buildings[J].Engineering Geology,2004,73(2):297-309.
[4]尹志刚,任玉珊,周静海,等.洪水作用下村镇住宅的力学响应试验研究[J].灾害学,2010,25(B10):127-130.
[5]李英民,韩 军,刘立平.ANSYS在砌体结构非线性有限元分析中的应用研究[J].重庆建筑大学学报,2006,28(5):90-96.
[6]高 丽,曾晓云,王 勇.基于ANSYS的钢筋混凝土梁非线性分析若干问题研究[J].水利与建筑工程学报,2011,9(2):92-94.
[7]王述红,唐春安,朱浮声,等.砌体结构开裂过程细观损伤数值模拟及其分析方法[J].建筑结构学报,2003,24(2):64-69.
[8]李 妍,孟广伟,尹新生.混凝土多孔砖砌体及砌体材料弹性模量取值研究[J].新建筑材料,2009,36(3):23-26.
