基于实测应变反演大坝混凝土实际徐变度
2012-09-26黄耀英周宜红
黄耀英,郑 宏,周宜红
(1.三峡大学 水利与环境学院,湖北 宜昌 443002;2.中国科学院武汉岩土力学研究所,岩土力学与工程国家重点实验室,湖北 武汉 430071)
混凝土的徐变与加荷时混凝土的龄期有关,在混凝土工程应力场仿真分析以及大坝耐久性分析时需要考虑混凝土的徐变因素.为了获得徐变参数,需进行大投入、大尺寸全级配徐变试验;即使进行室内小尺寸徐变试验,工作量也很大,且费时.因此,只能针对有限个龄期(通常为5,6个龄期)进行试验,然后采用徐变度表达式对这些室内徐变值进行拟合,以获得任意加荷龄期和任意持荷时间的徐变值[1].目前工程上常采用的混凝土徐变度表达式是阿鲁久涅扬首先给出并经朱伯芳[2-3]改进的8参数徐变度公式.由于混凝土徐变度表达式比较复杂,包含的参数较多,以往主要采用试凑法.针对室内徐变试验值公式拟合的问题,朱伯芳[2-3]建议采用复合型等优化方法来确定这些参数;李洋波等[4]采用复合型法求解了徐变度公式中的8个参数;陈志华等[5]基于演化程序对混凝土徐变参数进行了识别.
由于室内试验的局限性(小试件、湿筛、理想养护条件等),通过室内徐变试验获得的徐变参数难免与实际情况存在一定差异.吴相豪等[6]将计算位移和实测位移的残差加权平方和作为徐变度参数反演优化问题的目标函数,采用可变容差法初步探讨了徐变度4参数的反演,由于变形监测系统一般在大坝竣工时才安装,因此该方法一般只能获得晚龄期混凝土的徐变特性.在实际混凝土工程中埋设了一些应变计组和无应力计对大坝的应力应变进行监测,基于实测应变反演的徐变度可较全面反映早龄期和晚龄期混凝土的徐变特性,但基于应变计组和无应力计实测应变反演大坝混凝土徐变度至今尚未见有关文献报导,为此,本文探讨基于应变计组和无应力计实测应变反演大坝混凝土实际徐变度.
1 基本原理
基于应变计组实测应变反演大坝混凝土实际徐变度,涉及到应变计组实测应变的获得、施工期应变计测值统计模型、无应力计测值统计模型,以及基于实测应变和计算应变的优化反演模型的建立等多个环节,以下逐一介绍.
1.1 应变计组实测应变
在实际混凝土工程中,一般采用无应力计来监测温度应变、湿度应变和自生体积变形等自由体积变形.通过无应力计实测的自由体积应变可用下式[7]表示

式中:αΔT为温度应变,α为热膨胀系数;G(t)为自生体积变形;εw为湿度应变.
在大体积混凝土中,自由应变ε0由于受周围混凝土或其他边界的约束而引起内部应力,因此混凝土内部任一点的实测总应变εm由与应力相当的应变和自由应变两部分组成[7].

式中:ε为外力和内力引起的应变,也就是与应力相当的应变.
由于实际混凝土工程为复杂应变状态,确定空间一点的应变状态至少需要监测6个方向的应变.由于剪切应变一般不能直接监测获得,在实际工程上,一般采用6向(四面体)、7向或9向应变计组来获得6个方向以上的正应变,然后根据任意方向的应变εN与正应变、剪切应变的关系公式来计算空间6个独立的应变分量.
1.2 混凝土热膨胀系数的反演和自生体积变形的分离
由混凝土自生体积变形的试验资料可知,一般初期自生体积变形变化大,随后呈单调递减趋势[8].参考朱伯芳[9]提出的混凝土力学性能随龄期变化的组合指数公式,本文采用3个指数公式累加来描述自生体积变形的变化规律.对于温度应变分量,则采用无应力计的温度作为因子,而大体积混凝土内的湿度变化不大,不另选因子,由此建立无应力计测值统计模型为

式中:温度分量f(T)=b0+b1T;自生体积变形分量f(G(t))=b2(1-e-C1t)+b3(1-e-C2t)+b4(1-e-C3t);bi(i=0~4)为回归系数;Ci(i=1~3)为常数,根据回归经验,取C1=0.3,C2=0.05,C3=0.005.
采用逐步回归分析法获得无应力计测值的统计模型回归系数后,自动分离出温度变形分量和自生体积变形分量,对比式(3)和式(1),可以认为系数b1即为热膨胀系数,即b1=α.
对无应力计测值建立统计模型来反演热膨胀系数和分离自生体积变形,一方面可以克服采用不同的降温时段反演获得的热膨胀系数具有较大差异的缺点;另一方面,分离出的自生体积变形为降噪后的曲线表达式,便于有限元计算.
1.3 施工期应变计测值统计模型
由于施工期上下游均为围堰,整个大坝不承受水荷载.因此,施工期的应变统计模型包含自重分量、温度分量和时效分量.施工期,大坝混凝土逐层浇筑,坝体逐步上升,对于坝体内某一固定测点来说自重分量仅与坝体上升的高度有关,即自重分量与h,h2和h3呈线性关系;温度分量采用应变计温度和周期项作为因子;采用3个指数公式累加来描述时效分量的变化规律,由此,本文建立的施工期应变统计模型为

式中:fw(h)为自重分量;h为测点以上混凝土浇筑厚度;fT(T)为温度分量;T为应变计温度;ft(t)为时效分量;t为时间.a0为常数项,n为自重分量因子数,一般n=3,对于边施工边封拱的拱坝n=4或5,ai(i=1~3),bi(i=1~4),ci(i=1~3)分别为回归系数,A,B,C为常数,参考混凝土徐变试验以及根据回归经验,取A=0.3,B=0.05,C=0.005.
本文采用逐步回归分析法获得式(4)中的回归系数.由于应变测值受到多种环境因素的复杂影响并存在监测误差,具有某种程度的不确定性,建立施工期应变统计模型,获得降噪后的变化曲线,便于和计算应变建立目标函数,进行参数反演.
1.4 混凝土徐变度
《水工混凝土试验规程》(SL352-2006)指出混凝土压缩或拉伸徐变试验是在恒定的受压或拉伸荷载(一般为破坏荷载的30%左右)作用下,测量随时间增长的变形.由于作用荷载较小,测量的徐变变形一般为黏弹性变形,分可逆徐变变形与不可逆徐变变形.目前工程上常采用的混凝土徐变度表达式是阿鲁久涅扬首先给出、经朱伯芳等改进的弹性徐变理论式,由于不可逆徐变变形较小,常采用8参数的徐变度公式来描述弹性可逆徐变变形.徐变度表达式为[2]

式中:fi,gi,pi,ri(i=1,2),D,s均为常数,且一般均大于零;t为时间;τ为加荷龄期.
在上式中,一般取r1>r2,以使等号右边第1项代表持荷早期的可逆徐变;第2项代表持荷晚期的可逆徐变;第3项代表不可逆的徐变变形.在实际工程中,一般认为第3项较小,将其忽略,仅取前2项,即8参数徐变度.
1.5 基于应变计组实测应变反演大坝混凝土徐变度
由于将应变计组测值转化为实际应力的计算环节多,各个环节带入的误差和误差传递,使最终获得的应力成果精度降低,为此,本文采用应变计组实测应变和计算应变建立目标函数,反演大坝混凝土实际徐变度.
1.5.1 反演参数 考虑到多参数反演存在不适应性,为此,混凝土热膨胀系数采用无应力计测值统计模型的反演值.文献[8]指出湿筛和全级配混凝土的弹性模量较为接近,因此,混凝土随龄期增长的弹性模量取设计值,本文重点反演可逆徐变度表达式的8个参数,将各待定参数记为设计变量X,即
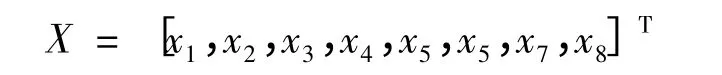
从物理概念上来看,一般要求xi≥0;且一般取r1>r2,即x4>x8.
在实际反演分析时,先对室内徐变资料采用优化算法确定徐变度表达式的8个参数;然后在此基础上,确定反演初始值.
1.5.2 反演优化模型 首先根据施工进度、气象资料、温控措施等进行温度场仿真分析,然后进行应力场仿真分析.在应力场仿真分析时,输出应变计组所在单元高斯点处的计算应变εc,如果应变计组位置与单元高斯点位置不一样,则采用应变计组位置临近高斯点采用插值获得,然后将计算应变和实测应变的残差平方和作为参数反演优化问题的目标函数,以寻求大坝混凝土的实际徐变度参数,即

式中:εm(i,j)和εc(i,j)分别为tj时刻的第i个实测应变和计算应变;n1为独立的应变分量数;n2为仿真计算中采用的时间段数.
为方便分析问题,本文取n1=3,即采用3个正应变进行反演分析;时间段数n2=10.当目标函数达到目标误差时,所得到的徐变参数即为最优参数.
式(6)为一个非线性规划中的约束极值问题,本文采用复合型法进行求解.复合型算法在文献[10]中有详细介绍,本文不再赘述.本文采用Visual Fortran编制了复合型法优化反分析程序.
由于计算应变的时刻与实测应变的时刻有时不一致,本文采用线性插值来获得同一时刻的计算应变和实测应变.
另外,实测应变是相对基准时刻的相对值,因此,必须将各时刻的计算应变减去基准时刻的计算应变,获得相对基准时刻的相对计算应变,然后再结合实测应变,采用式(6)计算目标函数.
1.5.3 反演方法 反演分析方法有逆反分析法和正反分析法两种.本文采用正反分析法进行8参数徐变度参数反演[11],即采用复合型法调用大体积混凝土应力场仿真分析程序获得计算应变.
1.6 仿真分析说明
大体积混凝土温度场和应力场仿真分析计算原理在文献[2]中有详细叙述,这里不再赘述.本文采用Visual Fortran编制了大体积混凝土温度场和应力场仿真分析程序[12].在仿真分析时,由于大体积混凝土内部湿度变化较小,本文没有考虑湿度变形;对于自生体积变形,通过建立无应力计测值统计模型来获得自生体积变形的表达式f(G(t)),然后采用增量法将自生体积变形耦合到大体积混凝土应力场仿真分析程序.由式(3)可得自生体积变形的增量为
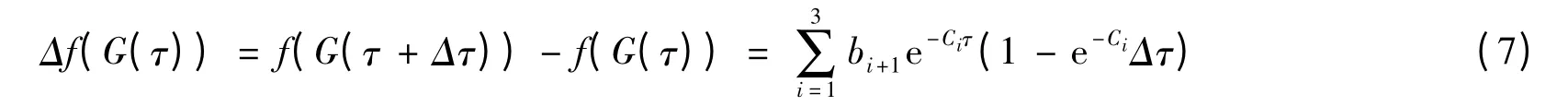
式中:Δτ为增量时间.由于混凝土自生体积变形与龄期有关,所以在计算自生体积变形时,式(3)中的时间t为龄期τ.
2 实例分析
西南某建设中的特高拱坝位于四川省雷波县和云南省永善县接壤的金沙江峡谷段,拦河大坝为混凝土双曲拱坝,坝顶高程610 m,最大坝高285.5 m,大坝共31个坝段.为了对大坝混凝土的应力应变进行监测,在坝体混凝土里埋设了差阻式应变计组和无应力计进行监测.该大坝埋设的应变计组为四面体6向应变计组,根据应变计布置的不同,分四面体a型和四面体b型应变计组.选取该大坝16#河床坝段EL.372高程处的应变计组和无应力计测值反演大坝混凝土徐变度,该应变计组为四面体a型应变计组,配套埋设的无应力计距离应变计组1 m左右,由大坝混凝土的分区可知,该仓混凝土为A区C40混凝土.
2.1 无应力计测值和应变计组测值分析
按1.2节的原理建立无应力计测值统计模型,并采用逐步回归分析法确定各系数,回归复相关系数为0.994.反演的混凝土热膨胀系数为5.88×10-6/℃,小于混凝土设计热膨胀系数6.5×10-6/℃;分离出的自生体积变形为f(G(τ))=10.8361(1-e-0.3τ)-25.9212(1-e-0.05τ)-42.2901(1-e-0.005τ)×10-6.当τ→∞,f(G(τ))→-57.375×10-6,大于该混凝土室内试验的自生体积变形-40×10-6.无应力计实测值、拟合值、与统计模型分离出的自生体积变形如图1所示.
通过引入一个转化矩阵,即可方便地由四面体6向实测应变获得6个实测应变分量.按1.3节的原理建立施工期应变计测值统计模型,为便于分析,对扣除温度应变的应变计测值采用逐步回归分析法确定各系数,回归模型的复相关系数均在0.958以上,为节省篇幅,以下仅给出扣除温度应变的x向应变实测值、拟合值与混凝土浇筑厚度对比图(见图2).

图1 无应力计实测值、拟合值与自生体积变形 Fig.1 Measured value and fitted value of no stress plan and selfgrown volume deformation
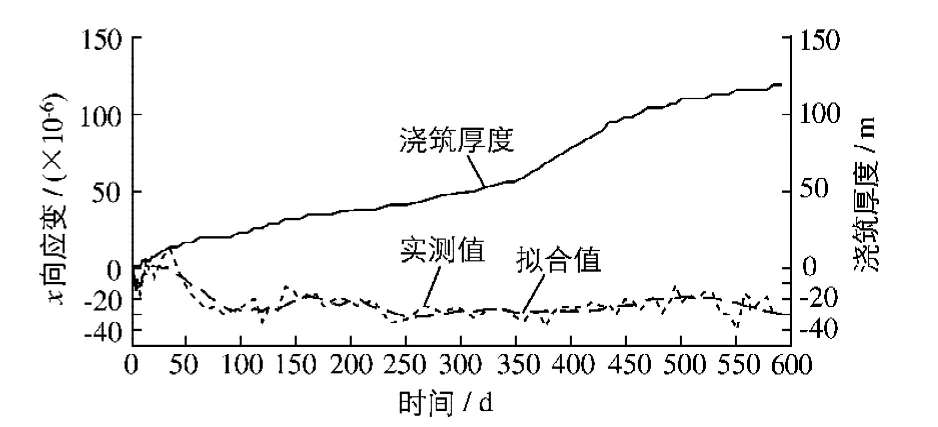
图2 扣除温度应变的x向应变测值、拟合值与浇筑厚度Fig.2 Measured strain value,fitted strain value in concrete placing layer thickness
2.2 温度场和应力场仿真分析
由于本文采用正反分析方法结合实测应变反演徐变度表达式的8个参数,这需要不断调用仿真分析程序获得计算应变,如果进行全坝全过程仿真分析,计算工作量极大.为分析问题方便,本文仅建立包含应变计组所在浇筑仓的8个混凝土浇筑仓的有限元模型,这8个浇筑仓层厚均为3 m,分6个坯层浇筑,在高度方向按0.5 m一层进行剖分,建立的有限元模型单元数为3 840,结点数为4 851.有限元模型见图3.由于应变计组位置与单元高斯点位置不完全一样,计算时,采用应变计组位置临近高斯点采用(内)插值获得应变计组位置的应变.
2.2.1 温度场仿真分析 8个混凝土浇筑仓中,下面6个浇筑仓的水管间距为1.0 m×1.5 m,上面2个浇筑仓水管间距1.5 m×1.5 m,采用朱伯芳提出的水管冷却等效热传导法考虑水管冷却效果,仓间间歇时间为实际间歇时间,混凝土绝热温升和表面放热系数采用基于实测温度的反演值,其余热学参数采用设计值,通水温度、通水流量和通水时间采用实际通水方案,环境气温采用实际日平均气温,仿真分析时间2010-04-13—2010-06-27,计算时间步长为0.25 d,温度场仿真分析表明,计算温度与实测温度吻合良好,为节省篇幅,不再给出对比图.
2.2.2 应力场仿真分析 在温度场仿真分析的基础上,进行应力场仿真分析.应力场仿真分析时,考虑温度荷载、自重、徐变以及自生体积变形等.仿真分析时间和计算时间步长同温度场仿真分析.
2.3 参数反演及初值确定
2.3.1 参数反演 按前文所述,混凝土热膨胀系数取基于无应力计测值统计模型的反演值5.88×10-6/℃.因试验表明,混凝土湿筛弹性模量和全级配试验弹性模量较为接近,因此混凝土弹性模量采用室内试验值E(τ)=42.5(1-e-0.1τ)GPa,τ为混凝土龄期,混凝土徐变度采用8参数徐变度表达式,为待反演参数.2.3.2 反演初值的确定 应变计组埋设的浇筑仓混凝土为C40混凝土,结合该混凝土室内徐变试验值,优化确定徐变度表达式的8个参数(称拟合徐变度),然后在拟合徐变度参数的基础上,确定反演分析初值.室内试验优化确定的拟合徐变度表达式为

2.4 反演结果及分析
由于复合型法等优化反演方法在反演分析时,容易陷入局部最优,为此,在反演过程中,寻优20次后,在当前最优值的基础上按一定幅度扰动,如此反复,获得最优反演值,由此得到徐变度表达式(称反演徐变度)为
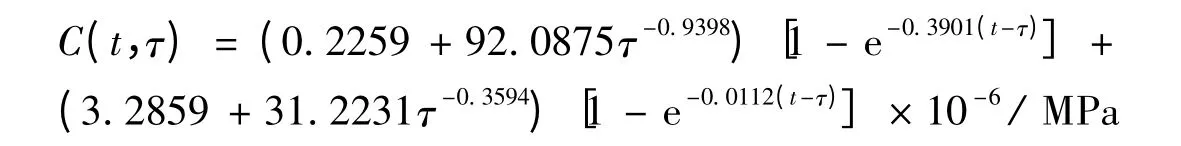
分别采用室内试验的拟合徐变度和基于实测应变的反演徐变度进行应力场仿真分析,以下给出应变计组所在位置的x向和y向计算应变和实测应变对比图(见图4),图中应变扣除了温度应变.由图可见,计算应变和实测应变的变化规律接近,总体来说,相对拟合徐变度的计算应变而言,采用反演徐变度计算的应变更接近于实测应变.
图3 计算模型Fig.3 FEM model

图4 实测应变和计算应变对比Fig.4 Measured strain and calculated strain
2.5 反演徐变度与室内徐变度对比分析
室内混凝土徐变值、基于室内徐变值的拟合徐变度和基于实测应变的反演徐变度对比见图5.其中,缺少加荷龄期为3和63 d的室内混凝土徐变值.

图5 不同加荷龄期时的徐变过程线比较Fig.5 Creep curves of different loading ages
由图可见:(1)拟合徐变度和室内徐变值吻合的效果良好,这说明拟合徐变度表达式的拟合精度高.(2)当加荷龄期较小时,反演徐变度较室内徐变值小,如加荷龄期为7 d时,持荷360 d,反演徐变度和室内徐变值的比值约为0.895;在加荷龄期为28 d时,反演徐变度在初期时小于室内徐变值,在后期反演徐变度和室内徐变值趋于接近;当加荷龄期较大时,反演徐变度在初期小于室内徐变值,在后期则大于室内徐变值,如加荷龄期为180 d时,持荷360 d,反演徐变度和室内徐变值的比值约为1.126.
3 结语
对基于应变计组实测应变反演大坝混凝土实际徐变度进行了初步探讨,得到如下结论:
(1)由于应变测值受到多种环境因素的复杂影响并存在监测误差,建立了施工期应变统计模型,获得降噪后实测应变曲线.然后基于实测应变和计算应变,建立了反演徐变度表达式8参数的非线性规划约束极值问题,给出了反演徐变度表达式8参数的步骤和注意事项.
(2)结合西南某建设中的混凝土坝埋设的6向四面体应变计组和无应力计实测值,基于温度场和应力场仿真分析程序,采用复合型法优化反演确定了徐变度表达式的8个参数.采用反演徐变度计算的应变与实测应变吻合效果较好.
(3)当加荷龄期较小时,反演徐变度较室内徐变值小,如加荷龄期为7 d时,持荷360 d,反演徐变度和室内徐变值的比值约为0.895;在加荷龄期为28 d时,反演徐变度在初期小于室内徐变值,在后期和室内徐变值趋于接近;当加荷龄期较大时,反演徐变度在初期小于室内徐变值,在后期则大于室内徐变值,如加荷龄期为180 d时,持荷360 d,反演徐变度和室内徐变值的比值约为1.126.
(4)由于目前进行优化反分析时,一般采用正反分析方法,需要不断调用仿真分析有限元程序计算,而基于实测应变反演混凝土徐变度8参数,需要进行温度场仿真分析,然后进行应力场仿真分析,涉及的计算环节多,问题复杂,而且计算工作量极大.本文进行优化反演时,仿真分析的计算时间不长,可能在一定程度上影响反演精度,该问题有待进一步研究.
[1]SL352-2006,水工混凝土试验规程[S].(SL352-2006,Test code for hydraulic concrete[S].(in Chinese))
[2]朱伯芳.大体积混凝土温度应力与温度控制[M].北京:中国电力出版社,1999:95-100.(ZHU Bo-fang.Thermal stresses and temperature control of mass concrete[M].Beijing:China Eelectric Power Press,1999:95-100.(in Chinese))
[3]朱伯芳.混凝土的弹性模量、徐变度和应力松弛系数[J].水利学报,1985(9):54-61.(ZHU Bo-fang.Concrete's modulus of elasticity,unit of creep and stress relaxation parameter[J].Journal of Hudraulic Engineering,1985(9):54-61.(in Chinese))
[4]李洋波,李翔,黄达海.混凝土徐变度反演分析方法[J].三峡大学学报:自然科学版,2005,27(2):134-136.(LI Yang-bo,LI Xiang,HUANG Da-hai.Back analysis method for unit creep of concrete[J].Journal of China Three Gorges University(Natural Sciences),2005,27(2):134-136.(in Chinese))
[5]陈志华,陕亮,关富玲.基于演化程序的混凝土徐变参数识别[J].长江科学院院报,2005,22(2):47-49.(CHEN Zhihua,SHAN Liang,GUAN Fu-ling.Identification of concrete creep parameters based on evolution programs[J].Journal of Yangtze River Scientific Research Institute,2005,22(2):47-49.(in Chinese))
[6]吴相豪,吴中如,顾冲时,等.碾压混凝土拱坝徐变度反演分析方法[J].大坝观测与土工测试,2000,24(1):22-24.(WU Xiang-hao,WU Zhong-ru,GU Chong-shi,et al.Back analysis method for creep degree of roller compacted concrete arch dam[J].Dam Observation and Soil Testing,2000,24(1):22-24.(in Chinese))
[7]储海宁.混凝土坝内部观测技术[M].北京:水利电力出版社,1989:55-58.(CHU Hai-ning.Internal observation technology of concrete dam[M].Beijing:Hydraulic and Electric Power Press,1989:55-58.(in Chinese))
[8]朱伯芳,张超然.高拱坝结构安全关键技术研究[M].北京:中国水利水电出版社,2010:123-125.(ZHU Bo-fang,ZHANG Chao-ran.Researches on the structural safety of high concrete arch dams[M].Beijing:China WaterPower Press,2010:123-125.(in Chinese))
[9]朱伯芳.混凝土热学力学性能随龄期变化的组合指数公式[J].水利学报,2011,42(1):1-7.(ZHU Bo-fang.Compound exponential formula for variation of thermal and mechanical properties with age of concrete[J].Journal of Hydraulic Engineering,2011,42(1):1-7.(in Chinese))
[10]郭科,陈聆,魏友华.最优化方法及其应用[M].北京:高等教育出版社,2007:15-20.(GUO Ke,CHEN ling,WEI You-hua.Optimum method and application[M].Beijing:Higher Education Press,2007:15-20.(in Chinese))
[11]黄耀英,黄光明,吴中如,等.基于变形监测资料的混凝土坝时变参数优化反演[J].岩石力学与工程学报,2007,26(S1):2941-2945.(HUANG Yao-ying,HUANG Guang-ming,WU Zhong-ru,et al.Optimization inversion of concrete dam's time-dependent parameters based on deformation monitoring data[J].Chinese Journal of Rock Mechanics and Engineering,2007,26(Suppl1):2941-2945.(in Chinese))
[12]黄耀英,周宜红,周建兵.水管冷却热传导计算模型能量分析[J].水利水运工程学报,2012(1):78-82.(HUANG Yao-ying,ZHOU Yi-hong,ZHOU Jian-bing.Energy analysis of a pipe cooling thermal conduction calculation model[J].Hydro-Science and Engineering,2012(1):78-82.(in Chinese))
