圆柱体混凝土构件中氯离子扩散的解析研究

周 明，杨绿峰，2，陈 正，蒋琼明，洪 斌，胡春燕

(1．广西大学 工程防灾与结构安全教育部重点实验室，广西 南宁 530004;2．广西壮族自治区住房与城乡建设厅，广西 南宁 530028)

水运工程和海工建筑物如跨海大桥、海港码头等，通常采用钢筋混凝土结构，而海水中氯离子的侵蚀会导致结构中的钢筋锈蚀膨胀，从而造成混凝土结构腐蚀破坏．因此，探求氯离子扩散和分布规律是海工建筑物服役寿命预测和耐久性设计的关键．

混凝土中氯离子扩散的解析解法能给出海工建筑物中局部位置的氯离子浓度分布规律，并为研究混凝土结构的服役寿命、水运工程和海工建筑物耐久性设计提供理论依据．Callepardi［1］利用Fick第二定律研究建立了混凝土中氯离子一维扩散的控制方程．Takewake［2］、姚诗伟［3］分别得到了氯离子一维扩散的解析解．Suryavanshi［4］建立了半无限域氯离子二维扩散的误差函数形式解析解．杨绿峰等［5］考虑扩散系数的时变特性推导出了氯离子一维、二维扩散的时变解析解．孙伟等［6－7］研究了无限域和有限域氯离子扩散问题的理论模型，建立了多维多因素氯离子扩散控制方程，并推导了傅里叶解析解．

然而，实际混凝土结构中部分构件的截面为圆形，金祖权等［8］调查研究了具有圆环截面的海底隧道衬砌混凝土在多种因素下的冻融损伤，其中氯离子的腐蚀是其损伤的主要耦合因素之一，其它如跨海大桥的桥墩、海港码头承力柱等，它们同样面临严重的氯离子腐蚀问题．王显利等［9］基于有限差分法研究了圆形截面的氯离子扩散规律，分析了其耐久性，并开展了相应的实验研究工作［10］．解析解法使用简单，通常作为实验研究、数值方法的主要验证工具，而目前混凝土中氯离子的一维、二维扩散解析解都不适合用来描述氯离子沿圆形截面周边向混凝土内部扩散的问题，因此有必要开展圆形截面混凝土构件的氯离子扩散和浓度分布规律的解析研究．

圆形截面的氯离子扩散为平面扩散，其控制方程为二维扩散控制方程，本文根据二维扩散控制方程建立了氯离子沿圆柱构件周边向混凝土内部扩散的极坐标方程，并利用贝塞尔函数简化计算公式建立了圆形截面混凝土构件中氯离子浓度分布的解析解．

1 圆形截面解析解推导

当圆柱体混凝土构件的周边(顶面、底面除外)暴露于氯盐环境时，氯离子将沿柱面侵入混凝土中，并呈现二维扩散现象，可通过Fick第二定律来进行描述［1］:

其边界条件和初始条件为:

式中:Г为暴露于氯盐环境中的圆柱面;Ω为扩散域;P为扩散体中的任一点;t为试件暴露于氯盐环境的时间;Cs为试件表面氯离子浓度;C0为初始氯离子浓度．对于圆形截面试件，使用极坐标变换有:

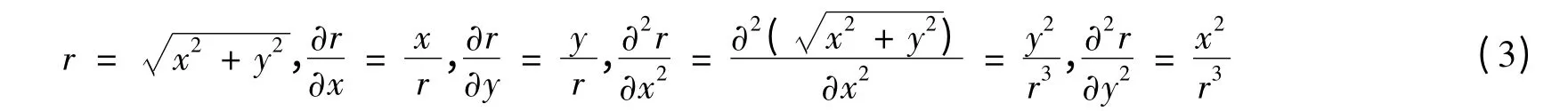
式(1)等号右边第1项可变换为:

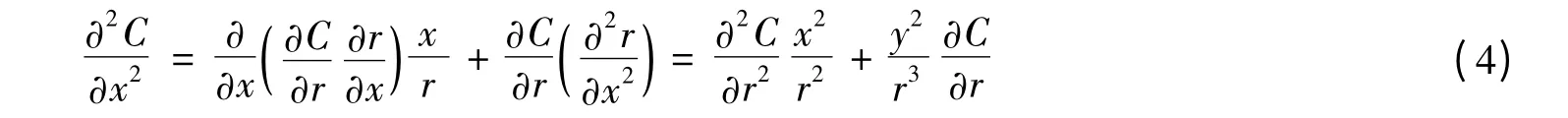
同理，式(1)等号右边第2项可变换为:

结合式(3)，将式(4)和(5)代入式(1)得:

式中:R为截面半径，其边界条件和初始条件为:

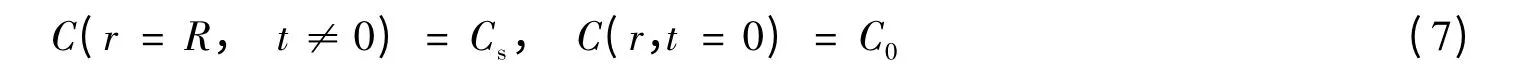
使用变量代换:

式(6)变为:

其边界条件和初始条件为:

根据变量分离法:

式(9)可以转化为2个一元微分方程:

式(13)的解为:

根据U的物理意义可知，当t→+∞时，U=0，相应地有T=0．据此可知，λ＞0．式(12)是二阶变系数微分方程，存在级数解［11］:

容易求得式(15)中的系数ai:

根据式(10)中的边界条件，结合式(15)和(16)，可得:

满足方程的λ有一系列的值，设为λ1，λ2，…，λn将之代回式(14)和(15)，则有:

令λn=β2n，同时采用第一类0阶和1阶贝塞尔函数:

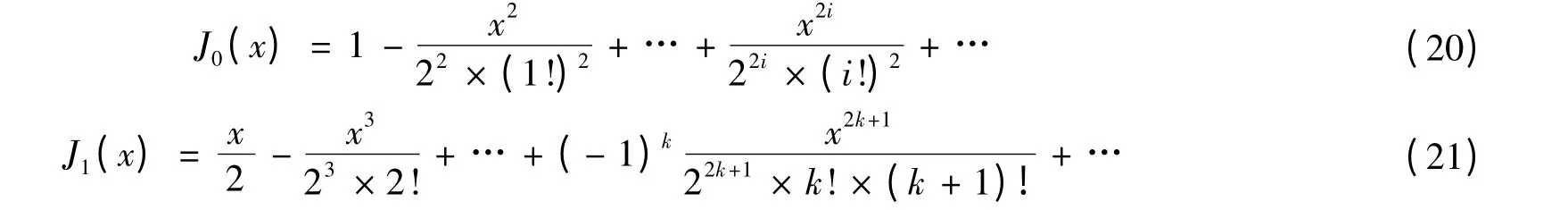
由叠加原理可得原问题的解为:

式中:βn由方程J0(βR)=0的根得到;An为待定系数，可以根据式(10)中的初始条件及贝塞尔函数的性质求得［12］:

根据式(8)，(22)和(23)，得到圆柱体内的氯离子浓度分布及其扩散过程的封闭解:

从上式可以看出，求解圆柱体混凝土构件中氯离子扩散过程和浓度分布的关键在于准确求解0阶、1阶贝塞尔函数J0(x)和J1(x)．但在实际工程中，圆形截面的半径通常较大，利用贝塞尔函数计算时需要的级数项多，相应的计算速度会随之而快速下降．为解决该问题，当x=βnr≥15．9时，可采用(25)中渐进计算公式［13］．计算贝塞尔函数，从而有效简化式(24)的求解过程．

2 算例分析

算例1:根据文献［14］提供的参数取值，利用普通硅酸盐水泥制作一批圆柱体试件，其横截面半径分别为200，500和900 mm，水灰比为0．65．当混凝土龄期为28 d时将圆柱体试件的上下表面用环氧树脂封闭，保留混凝土试件的柱面暴露于氯盐侵蚀环境中．根据文献［14］检测的结果，可知表面氯离子浓度为Cs=0．565%(氯离子质量占混凝土质量的百分比，下同)，混凝土扩散系数D=9．381×10－12m2/s=295．84 mm2/a．

首先直接使用贝塞尔函数公式(20)，(21)和(24)求解圆柱体试件暴露于氯盐环境10 a时氯离子在试件中的分布情况．同时，为了检验该计算结果，还采用商业有限元软件Ansys建立该算例的有限元计算模型，计算圆柱体混凝土中氯离子浓度．2种方法的计算结果如图1所示．从图1可以看出，2种方法的结果偏差较大，并且这种差异将随着圆柱体半径的增加而逐渐增大．

从宏观方面分析，氯离子沿混凝土圆柱形试件周边向混凝土内部扩散时属于二维扩散状态，当圆柱体构件的截面半径R逐渐增大直至R→∞时，试件中氯离子的扩散逐渐接近于一维扩散状态;由于在相同的条件下，处于二维扩散条件下混凝土中的氯离子浓度高于一维扩散，所以圆柱体混凝土试件中氯离子浓度应随着试件截面半径的增大而降低．从图1可以看出，直接使用贝塞尔函数公式求解得到的氯离子浓度随着圆柱体半径的增大而逐渐增大，并且逐渐偏离一维解析解，而有限元软件Ansys的求解结果与此恰好相反，且后者与上述宏观分析结论完全吻合．由此可知，直接利用贝塞尔公式计算氯离子扩散会导致错误结果．其原因在于，因为贝塞尔函数是一个多项式，且高次项与低次项之间有多个数量级的差异，而贝塞尔函数自身的值非常小，且收敛较慢，所以，如果不在程序设计时采取特别措施，就会发生大数吞小数现象，并造成较大的计算误差．因此，使用精确、有效的贝塞尔函数计算方法是准确求解圆形截面氯离子扩散和分布规律的关键．

将式(25)代入式(24)，建立圆柱体混凝土构件中氯离子沿柱面向内部扩散的解析计算公式，据此求解不同半径的圆柱体试件暴露于氯盐环境10 a时氯离子在试件中的分布情况，并与商业有限元软件Ansys的计算结果、氯离子一维扩散的计算结果相比较(见图2)．由图2可见，对于不同半径的圆柱体混凝土构件，本文建立的解析解与有限元商业软件Ansys的计算结果始终吻合良好，证明了本文方法的正确性．计算结果表明随着圆柱体混凝土构件半径增大，氯离子浓度逐渐减小，且逐渐逼近氯离子一维扩散的结果，这与前文中的宏观分析结论相吻合，进一步说明本文建立的解析解是合理的．

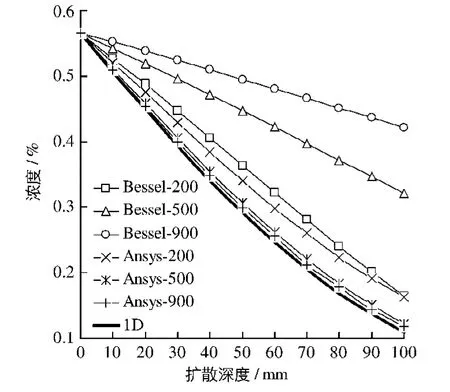
图1 贝塞尔级数计算试件中氯离子浓度 Fig．1 Chloride distribution resulting from Bessel series

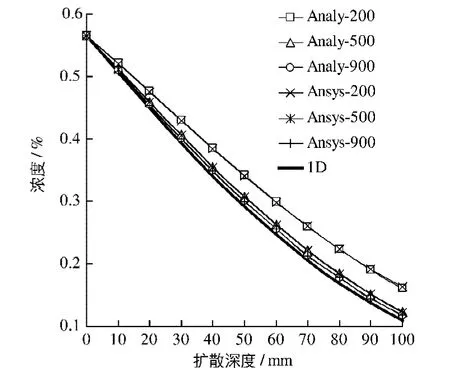
图2 贝塞尔渐进公式计算试件中氯离子浓度Fig．2 Chloride content from simplified Bessel function

算例2:设有1个半径为200 mm的圆柱体混凝土构件(用C表示)和1个截面尺寸为400 mm×400 mm的矩形截面棱柱体混凝土构件(用R表示)，圆柱体和棱柱体混凝土构件的柱面都处于相同的含氯离子环境中．已知测得混凝土构件表面氯离子浓度Cs为1%，混凝土中初始氯离子浓度C0为0，混凝土扩散系数D为1×10－12m2/s=31．536 mm2/a．首先采用本文方法，通过式(24)和式(25)计算圆柱体混凝土构件内氯离子浓度分布．然后根据文献［5］的计算公式，求得棱柱体混凝土构件矩形截面的对角线上氯离子浓度的分布，计算结果如图3所示．

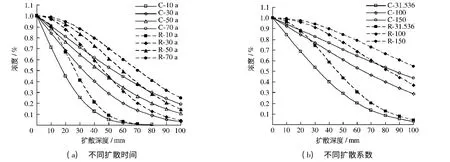
图3 不同扩散时间和扩散系数的氯离子分布Fig．3 The chloride distribution of different diffusion time and different diffusion coefficients

图3 (a)为混凝土构件暴露于氯盐环境10，30，50和70 a时的氯离子浓度分布．图3(b)为混凝土扩散系数分别取31．536，100和150 mm2/a，且暴露于氯盐环境30 a时混凝土构件内部的氯离子浓度分布．由图3(a)可以看出，矩形截面混凝土构件内氯离子浓度明显高于圆柱体试件，并且随时间的增长这种趋势更加明显．图3(b)表明，棱柱体混凝土构件的氯离子浓度高于圆柱体混凝土构件，并且随混凝土扩散系数的增加，该趋势更加明显．由于海洋混凝土结构的耐久性取决于构件内钢筋周围集聚的氯离子浓度及由此诱发的钢筋锈蚀时间［15］，因此在海洋侵蚀环境条件和钢筋保护层厚度等条件相同时，使用圆形截面代替矩形截面构件可以避免矩形截面构件拐角处出现过早破坏的现象，从而有效地提高海洋混凝土结构的服役寿命．

3 结语

本文通过分离变量法，利用贝塞尔函数简化计算公式建立了圆形截面混凝土试件中氯离子二维扩散规律和浓度分析的解析解，并通过与商业有限元软件Ansys计算结果对比，验证了本文建立的解析解的正确性．

在相同情况下，矩形截面混凝土构件中氯离子二维扩散导致氯离子浓度高于圆形截面构件，因此，暴露于氯盐环境的混凝土构件，使用圆形截面代替矩形截面可以避免矩形截面拐角处出现过早破坏的现象，有利于提高混凝土结构的耐久性．

［1］COLLEPARDI M，MARCIALISA，TURRIZZANI R．The kinetics of penetration of chloride ions into the concrete［J］．Cemento(Italy)，1970，4:157-164．

［2］TAKEWAKE K，MASTUMOTO S．Quality and cover thickness of concrete based on the estimation of chloride penetration in marine environments［C］∥MALHOTRA V M．Proc 2ndInt Conf Concr Marine Envir，ACI SP-109，1988:381-400．

［3］姚诗伟，吴萍．氯离子扩散方程的解析解［J］．港工技术与管理，2006(5):1-9．(YAO Shi-wei，WU Ping．Analytical solution for chloride diffusion［J］．Port Engineering Technology and Management，2006(5):1-9．(in Chinese))

［4］SURYAVANSHI A K，SWAMY R N，CARDEW G E．Estimation of diffusion coefficient for chloride ion penetration into structural concrete［J］．ACI Materials Journal，2002，99(5):441-449．

［5］杨绿峰，李冉．混凝土中氯离子二维扩散规律的解析研究［J］．水利水电科技进展，2009，29(3):20-23．(YANG Lufeng，LI Ran．Analytical study of two-dimensional diffusion of chloride ion in concrete［J］．Advances in Science and Technology of Water Resources，2009，29(3):20-23．(in Chinese))

［6］余红发，孙伟，麻海燕．混凝土氯离子扩散理论模型的研究Ⅰ－基于无限大体的非稳态齐次与非齐次扩散问题［J］．南京航空航天大学学报，2009，41(2):276-280．(YUHong-fa，SUNWei，MA Hai-yan．Diffusion model of chloride in concrete I-homogeneous and inhomogeneous diffusion in infinite body［J］．Journal of Nanjing University of Aeronautics＆Astronautics，2009，41(2):276-280．(in Chinese))

［7］余红发，孙伟，麻海燕．混凝土氯离子扩散理论模型的研究Ⅱ－基于有限大体的非稳态齐次与非齐次扩散问题［J］．南京航空航天大学学报，2009，41(3):408-413．(YUHong-fa，SUNWei，MA Hai-yan．Diffusion model of chloride in concreteⅡ－homogeneous and inhomogeneous diffusion in finite body［J］．Journal of Nanjing University of Aeronautics＆Astronautics，2009，41(3):408-413．(in Chinese))

［8］金祖权，赵铁军，侯保荣，等．海底隧道衬砌混凝土在多种因素下的冻融损伤［J］．广西大学学报:自然科学版，2010，35(1):90-95．(JIN Zu-quan，ZHAOTie-jun，HOU Bao-rong，et al．Freeze-thaw damage of lining concrete under multi-factors in subsea tunnel［J］．Journal of Guangxi University(Natural Science Edition)，2010，35(1):90-95．(in Chinese))

［9］王显利，吴智敏，郑建军．氯离子侵蚀圆形截面钢筋混凝土结构耐久性分析［J］．东北林业大学学报，2006，34(2):76-77，108．(WANG Xian-li，WU Zhi-min，ZHENG Jian-jun．Durability analysis of reinforced concrete structure with circular section under chlorine anion corrosion［J］．Journal of Northeast Forestry University，2006，34(2):76-77，108．(in Chinese))

［10］王显利，郑建军，吴智敏，等．圆形截面混凝土中的自由氯离子含量分布规律［J］．沈阳建筑大学学报:自然科学版，2006，22(6):890-894．(WANG Xian-li，ZHENG Jian-jun，WU Zhi-min，at al．The durability rules of free chloride concentration in circular section concrete element［J］．Journal of Shenyang Jianzhu University(Natural science)，2006，22(6):890-894．(in Chinese))

［11］BИ斯米诺夫．高等数学教程［M］．北京:人民教育出版社，1953:105－109．(BИCMИPHOB．The higher mathematics course［M］．Beijing:People's Education Press，1953:105－109．(in Chinese))

［12］王元明．数学物理方程与特殊函数［M］．北京:高等教育出版社，2004:101-127．(WANG Yuan-ming．Equations of mathematical physics and special functions［M］．Beijing:Higher Education Press，2004:101-127．(in Chinese))

［13］奚定平．贝塞尔函数［M］．北京:高等教育出版社，1998:93-121，184-187．(XI Ding-ping．Bessel function［M］．Beijing:Higher Education Press，1998:93-121，184-187．(in Chinese))

［14］张宝兰，卫淑珊．华南海港钢筋混凝土暴露十年试验［J］．水运工程，1999，3:6-13．(ZHANG Bao-lan，WEI Shu-shan．Reinforced concrete structure at sea port of South China after ten years expose［J］．Port＆Waterway Engineering，1999，3:6-13．(in Chinese))

［15］BEHROUZ SHAFEI，AZADEH ALIPOUR，MASANOBU SHINOZUKA．Prediction of corrosion initiation in reinforced concrete members subjected to environmental stressors:A finite-element framework［J］．Cement and Concrete Research，2012，42:365-376．