基于空间谱估计的多干扰源分辨技术研究

张官荣 ， 马建仓 ， 赵 玉 ， 程 胜

（1.西北工业大学 电子信息学院，陕西 西安 710129；2.空军工程大学 工程学院，陕西 西安 710038）

目标信号的分辨能力是反辐射导弹被动导引头设计的关键技术之一，也是检验其抗干扰性能的重要指标[1]。目前被动雷达导引头常用的信号分选方法主要为时频域分选，在多个干扰源情况下，目标信号参数的随机性与不确定性导致没有固定的参数可用于严格时序的波门分选，且信号流中包含多个频域、时域上参数变化或基本一致的脉冲序列时，只利用频域和时域参数很难完成分选任务[2，4]。为此，需要寻求新的多目标分选方法。

由于目标辐射源的空间位置不会发生突变，因此利用到达方向（DOA）这一较为稳定和可靠的目标参数，通过判别每个DOA的归属问题可以有效完成对多目标的分选或分辨。文中基于空间谱估计原理，提出了二维角度域多干扰源分选方法。空间谱估计理论中的MUSIC算法能够实现对多个信号源同时进行超分辨测向，对密集信号具有较高的空域分辨能力，并且定向精度较高[3]。将其应用于反辐射导引头，不但能够分辨多个目标信号，还可以有效提高测向精度。

1 空间谱估计测向原理

以线阵为例，假设有N个窄带信号从远场辐射到一个由个M传感器组成的天线阵上，以第一个阵元为参考点，相邻阵元间距为d。θi为第i个信号所对应的到达角，且-（π/2）≤θi≤π/2。 设阵元间隔小于信号的半波长 λ，即 λ/2≥d。

均匀线阵接收到的信号数学模型为

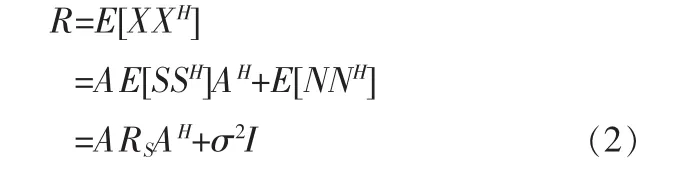
由于信号与噪声相互独立，数据协方差矩阵可以分解为与信号、噪声相关的两部分，利用信号子空间和噪声子空间的正交性，可构造空间谱函数如下[6，8]：

易知，上式确定的 N 个极大值所对应的 θi（i=1，2，…，N）就是目标信号的估计值。故对空间谱进行谱峰搜索即可得到信号的波达方向。

式（3）为经典MUSIC算法，其测向基本流程如图1所示。

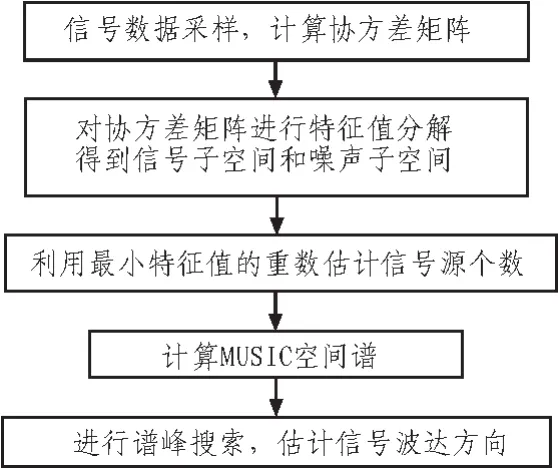
图1 经典MUSIC算法流程图Fig.1 Flow of traditional MUSIC algorithm

2 空域分选模型

2.1 测向天线阵

空间谱估计的测向性能与阵列天线的分布有关。其中，均匀线阵和均匀圆阵的分布形式最为常见。均匀线阵结构简单，但其只能提供一维方位角。均匀圆阵孔径小容易安装架设、各个方向响应全面，能同时实现二维超分辨测角，因此在电子对抗侦察研究和应用中获得青睐。

PRS采用半径为r的均匀圆阵天线，阵元数为M，圆阵在弹体中垂直放置。如图2所示，在天线圆阵所在平面建立直角坐标系，坐标原点同圆心重合。OZ轴为阵列平面的法线，且与导引头视轴重合，指向PRS头部方向，OX轴和OY轴在天线平面内，且与OZ轴构成右手关系。设目标入射到天线阵面的到达角可以用方位角θ和俯仰角φ来表示，方位角θ为目标与圆心的连线在XOY平面上的投影与Y轴的夹角 （逆时针旋转），且 θ∈[0，2π]；俯仰角 φ 为目标到圆心的连线与轴的夹角，且φ∈[0，π/2]。在实际应用中，PRS依靠目标与视轴的偏角进行跟踪，图中给出的角度α和β分别为目标跟踪的视线纵向偏角、横向偏角，且 α=＜TxzOZ，β=＜TyzOZ。

图2 PRS阵列天线结构示意图Fig.2 Structure of array antenna from PRS

PRS天线阵接收到的信号数学模型描述为：

均匀圆阵的导向矢量矩阵为：

接收数据的协方差矩阵为：

式中RS为信号协方差矩阵。

2.2 目标辐射源个数判断

对于时频域难以分辨的情况，如非相干诱偏系统中的多目标分辨，首先需要确定目标是单点源还是两（多）点源，即判断目标的个数。文中采用最小描述长度准则（MDL）进行辐射源个数估计。

MDL判据准则为一致性估计，其估计原理为：将特征值的算术平均和几何平均构成的对数似然函数和罚函数进行组合，通过求解组合函数的最小值获取目标个数的估计值。MDL准则的数学描述为

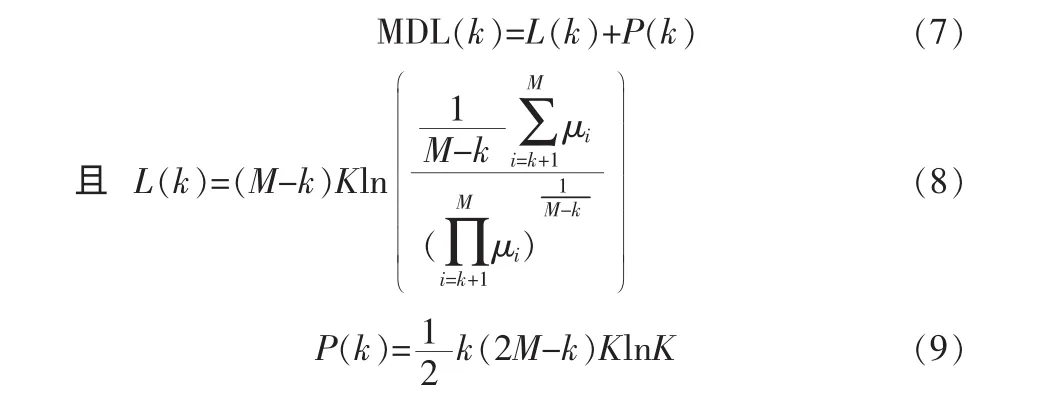
式中：L（k）为对数似然函数；P（k）为罚函数；k 为待估计的目标个数（自由度）；K为快拍数。

故辐射源个数的估计可通过下式获取

2.3 目标辐射源DOA估计

RX特征分解后可以分为两部分

其中，Σ′S、Σ′N分别为信号和噪声的特征值组成的对角阵，且Σ′S由N个大特征值构成，Σ′N由M-N个小特征值构成。

由噪声子空间和导向矢量的正交性，根据公式（3）构造空间谱，进行谱峰搜索，得到各个辐射源目标的波达方向。由于求解目标DOA涉及到二维搜索，较为常用的二维搜索方法有求拐点法和变步长搜索法。文中采用变步长搜索法，其基本思想为：先利用较大的步长实现粗搜索，确定大致搜索区域，然后利用较小的步长实现细搜索，获取谱峰的精确位置，以保证估计算法的实时性和测向精度。

2.4 角度波门设置

导引头对多个干扰源正确分辨之后，通过设置角度波门对选定目标进行攻击。PRS根据目标与电轴的偏角进行跟踪，偏角与DOA估计值的转换关系为

根据公式（12）将DOA估计值转换为电轴偏角对角度波门进行设置。

3 仿真计算与分析

设ARM采用8元均匀圆阵，直径为0.28 m，雷达和诱饵构成两点源，信号载频同为2.65 GHz，雷达、诱饵的信噪比分别取15 dB和20 dB。设雷达和诱饵辐射源信号入射角分别为、，且背景噪声为与信号不相关的窄带高斯白噪声，数据快拍数为500。采用文中分辨算法得到测向分辨仿真谱图和等高线图如图3所示。

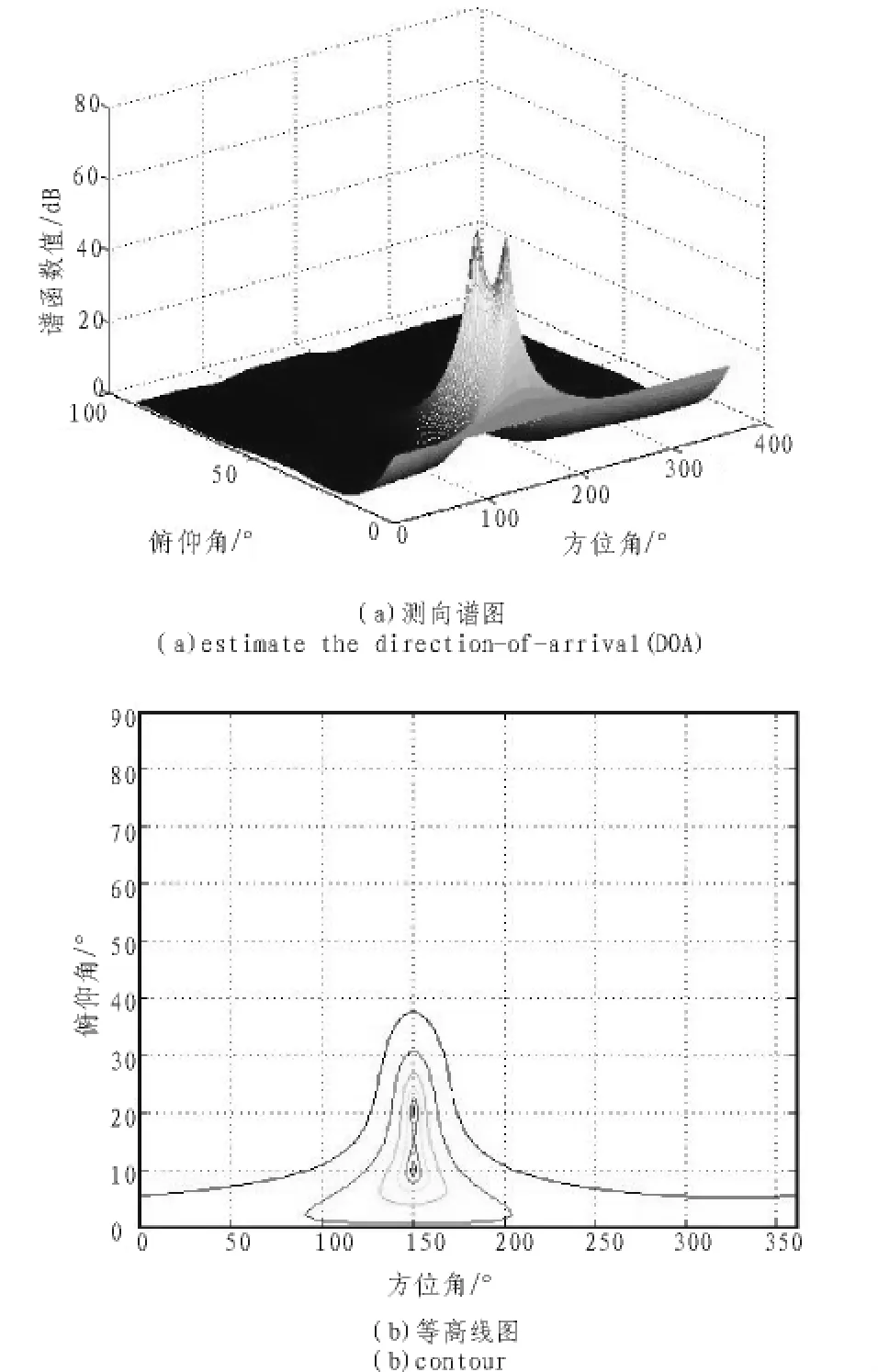
图3 MUSIC测向分辨谱图及等高线图Fig.3 Estimate the direction-of-arrival（DOA） spectrum and contour based on MUSIC

从图中可以看出导引头能够将雷达和干扰源区分开，并且正确估计出两辐射源的方位，测向估计结果为：雷达（150.15°，20.21°），诱饵（149.89°，10.10°）。

设辐射源DOA不变，快拍数为200，各进行100次蒙塔卡罗实验，得到分辨概率与信噪比、快拍数的关系如图4和图5所示。

图4 分辨概率与信噪比的关系图Fig.4 Relation between identification probability and SNR

从图中可以看出，导引头对两干扰源的分辨成功概率与接收信噪比以及快拍数有关。信噪比越大，成功分辨的概率越大；快拍数越大，即采样数越多，分辨成功概率也越大。

4 结 论

在空域分选基础上，文中采用空间谱估计测向算法，能够有效将多个密集信号从空域上分辨开，能够很好弥补传统分选算法需要精确提取目标参数的不足。仿真实验证明，该方法具有较优的多目标分辨能力和角度跟踪精度，并且能够对目标同时测向，在多个干扰源诱偏环境中具有较大的实用价值。如何减少算法的运算，提高实时性是下一步研究方向。

[1]王星.航空电子对抗原理[M].北京:国防工业出版社，2008.

[2]曲长文，陈铁柱.机载反辐射导弹技术[M].北京：国防工业出版社，2010.

[3]SI Xi-cai，CUI Dong-huai，SI Wei-jian.Technologies of ARM contradict LIP radar and bait[J].Systems Engineering and Electronics，2005，27（9）：27-30.

[4]徐松涛，杨邵全.被动单脉冲导引头干扰源角度分辨[J].西安电子科技大学学报，2004，31（1）:103-105.

XU Song-tao，YANG Shao-quan.Angularresolution of jammers of the passive monopulse seeker[J].Journal of Xidian University，2004，31（1）:103-105.

[5]SHI Yu-le.A new DOA estimation algorithm of coherent signal[C]//IEEE 3rd international conference on signal processing systems，2011（8）:240-244.

[6]Siouris G M.Missile and Control System[M].New York:Springer-Verlag，2004.

[7]Salameh A，Tayem N.Conjugate MUSIC for Non-Circular source[C]//IEEE Int.Conf.Acoust， Speech， Signal Process，2006（4）:877-880.

[8]Shan Z，Yum T-SP.A conjugate augmented approach to direction-of-arrival estimation[J].IEEE.on SP，2005，53（11）:4104-4109.