肘板趾端表面裂纹在随机波浪载荷作用下的疲劳扩展预报

武锐锋，黄小平

（上海交通大学 海洋工程国家重点实验室，上海 200240）

1 引 言

船舶与海洋结构物服役在复杂的海洋环境中，遭受风、浪、流等随机外载荷作用。一艘服役期为20年的船，所遭受的交变应力循环次数为108量级。大量的实船实例表明，船舶典型焊接接头部位较容易发生疲劳破坏，船舶结构破损在很大程度上是由于典型焊接接头的疲劳强度不足所致。由于制造工艺的原因，焊接接头难免存在初始缺陷和应力集中，这些缺陷会在交变载荷作用下引起局部结构的疲劳裂纹扩展。对接接头、T型接头和十字接头作为常见的焊接连接型式，其焊趾表面裂纹已得到了系统研究[1-3]，焊趾表面裂纹应力强度因子通常表示成K=MkKplate，Mk是应力强度因子修正系数，Kplate是平板表面裂纹的应力强度因子，以Newman-Raju[4]提出的表面裂纹应力强度因子计算公式最具代表性。肘板、加强筋等结构也是常见的船舶构件，这些构件与船体其他构件连接的趾端，很容易发生疲劳破坏，是疲劳校核的关键点，其疲劳断裂性能也是设计者极为关注的。趾端与T型接头类似，所不同的是趾端裂纹扩展会超过焊趾的影响范围。一些学者对趾端裂纹扩展进行了试验研究[5-7]，但对趾端裂纹应力强度因子及其修正系数的研究还比较少。Paris公式适用于常幅载荷作用下的裂纹扩展，而对于长期遭受变幅载荷作用的船舶与海洋结构物而言，黄小平等[8]提出的变幅载荷作用下的裂纹扩展率单一曲线模型能更好地预报疲劳寿命。本文计算趾端表面裂纹应力强度因子采用Newman-Raju[4]公式，并引入适当的修正系数Mk。基于三维有限元分析，研究了趾端表面裂纹应力强度因子修正系数的变化规律，并与BS7910中T型节点焊趾表面裂纹应力强度因子公式计算结果作了对比，通过用有限元和T型节点公式两种方法计算应力强度因子预报的肘板趾端表面裂纹疲劳寿命的对比，并针对某客滚船趾端表面裂纹在一系列满足Weibull分布的疲劳应力幅作用下的裂纹扩展进行了预报。

2 变幅载荷作用下疲劳裂纹扩展预报

2.1 变幅载荷作用下裂纹扩展率单一曲线模型

迄今为止，在变幅载荷作用下裂纹的扩展率问题已有不少研究，研究人员们已提出了诸多代表性裂纹扩展率模型。黄小平等[8]就变幅载荷作用下结构的疲劳裂纹扩展寿命预测时所用到的裂纹扩展率模型及模型中的材料参数的选取进行了研究，提出了等效应力强度因子幅和单一裂纹扩展率曲线模型。

其中ΔKeq0，ΔKth0是等效于应力比R=0时的等效应力强度因子幅和应力强度因子幅门槛值，；C是Paris系数，m是裂纹扩展指数。

其中MR是载荷比的修正因子，黄小平在对压—压疲劳试验研究的基础上给出了修正，将-5≤R＜0扩展为R＜0；MP是载荷次序的修正因子，不考虑超载的影响时MP=1。

式中β，β1是形状系数。船海结构物在服役过程中受到的外力是不断变化的，因而R也是不断变化的。Paris公式只适用于常幅载荷作用下的裂纹扩展，而对于遭受变幅载荷作用的船舶与海洋结构物而言，变幅载荷作用下的单一曲线模型能更准确地预报疲劳寿命。黄小平[8]、施伟[9]等将变幅载荷作用下疲劳裂纹扩展的试验数据与单一曲线模型的计算结果进行了对比，验证了单一曲线模型能很好地模拟变幅载荷作用下的疲劳裂纹扩展。

3 趾端表面裂纹应力强度因子计算

在船体结构中，如图1所示的趾端较容易萌生裂纹，发生疲劳破坏。此种节点在船体中广泛存在，也是规范中疲劳校核的关键点。趾端处一般首先萌生表面裂纹，以表面裂纹的形式扩展。实际中表面裂纹的形状并不是规则的，分析中通常作简化处理，认为是半椭圆形表面裂纹，如图1所示。若要对疲劳裂纹的扩展进行分析，正确地计算表面裂纹的应力强度因子是非常关键的。

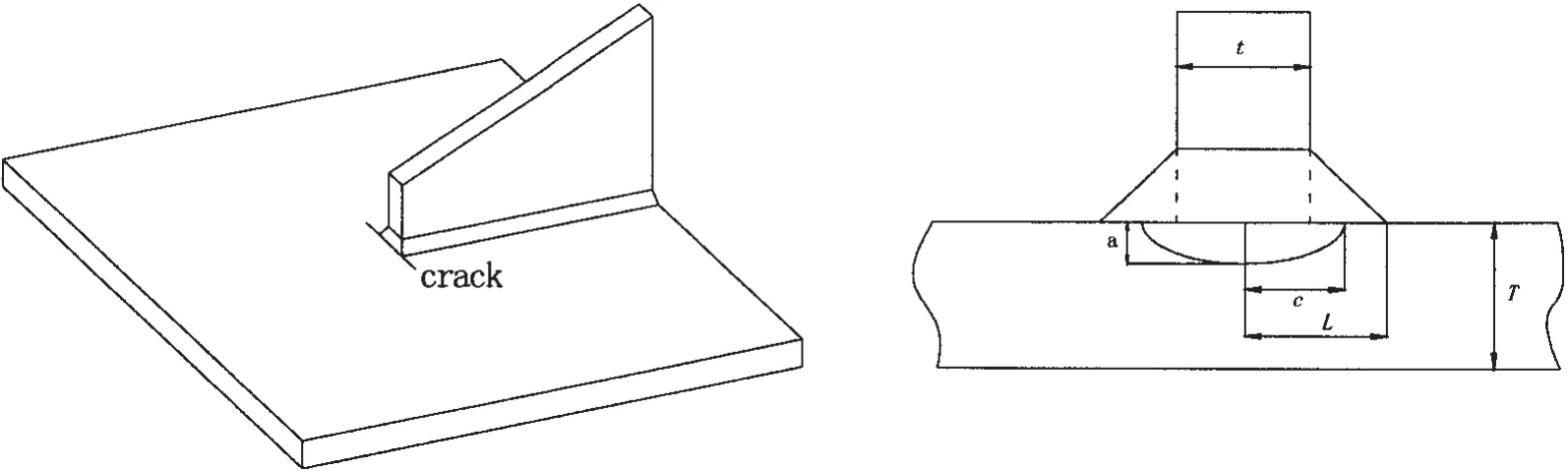
图1 趾端裂纹Fig.1 Crack at the weld toe

3.1 表面裂纹应力强度因子的计算

早在1979年，Newman-Raju就提出了具有代表性表面裂纹应力强度因子的计算方法。该方法具有计算精度高，适用范围大等特点，因而被广泛使用。焊接接头焊趾表面裂纹应力强度因子可以表示成K=MkKplate，Mk是应力强度因子修正系数，表示焊趾处应力集中引起的应力强度因子的增加。以Newman-Raju公式为基础，引入适当的修正系数，就可以计算得到不同的焊接接头焊趾表面裂纹的应力强度因子。拉伸载荷作用下表面裂纹应力强度因子的可表示为:

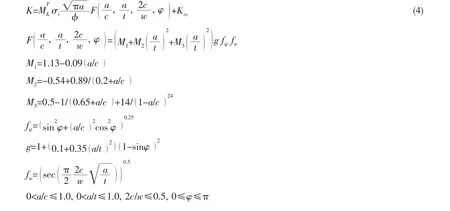
其中K为应力强度因子；σ为拉（压）应力；a为裂纹深度；c为裂纹半长；w为板宽；为拉伸应力作用下焊接结构应力强度因子放大系数；Krs为残余应力引起的应力强度因子。

3.2 应力强度因子修正系数的计算

焊趾处几何形状的变化会导致应力集中，因而计算焊趾处表面裂纹的应力强度因子时应该乘以一个应力强度因子修正系数MK。这个参数与焊接接头的种类、焊缝加强高和焊缝宽度等参数有关。Bowness和Lee[2]对T型焊接接头进行了广泛深入研究，并采用三维有限元进行了分析，在大量计算数据的基础上给出了准确度较高的Mk的计算公式，韩芸等[1]在此基础上提出了简化的计算方法，并与BS7910给出的计算公式进行了对比，验证了简化的合理性。此简化公式适用于对接焊接接头，十字型接头等多种焊接接头。

肘板趾端结构与T型接头类似，不同之处在于，T型焊接节点中裂纹始终在焊趾的影响范围内扩展，而肘板趾端表面裂纹裂纹扩展通常会超过趾端的影响范围。本文采用通用有限元软件ANSYS，对趾端表面裂纹末端和最深点的应力强度因子进行三维有限元分析，计算得到一系列修正系数，并与BS7910的推荐公式计算结果进行对比。在有限元软件ANSYS中，应力强度因子的计算有多种方法，本文采用位移外推法计算，经验证该方法具有足够的精度。修正系数的计算采用下式

式中Kweld是肘板趾端处表面裂纹的应力强度因子，Kplate是平板上相同表面裂纹的应力强度因子。

对教师的干预包括：①分级培训式健康教育；一级培训由研究团队的主要参与者担任。对象为干预学校的骨干教师(班主任、体育教师、心理健康教师、生理卫生教师、校医等)。二级培训：由骨干教师担任，对象为干预学校的全体教职员工。三级培训：由班主任利用班会和家长会，对家长和学生讲解肥胖的危害，及控制体重的意义。 ②运动干预：保证自身每日运动量不少于10 000步，同时监督儿童实现每日10 000步的目标；③对体育教师的干预：体育课要保证学生实际身体活动的时间达到30 min以上。

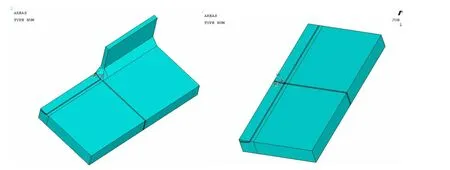
图2 三维结构模型Fig.2 3D models

有限元分析结构模型取自某客滚船180号肋位肘板与内底板连接处。分别对肘板-内底板结构和平板结构进行三维有限元建模，并计算得到裂纹最深点和裂纹末端的应力强度因子。韩芸等[1]通过分析指出，焊趾角、裂纹形状比和裂纹深度比等参数对修正整系数都有影响，但影响最为显著的是裂纹深度与板厚比，本部分主要考虑深度比对修正系数的影响。肘板厚度为t=12 mm，底板厚度为T=20 mm，趾端半长L=12 mm，结构两端施加大小为100 MPa的拉伸载荷，有限元结构模型如图2所示，裂纹细部网格模型如图3所示。取a/c=0.2，a/T=0.05～0.8。

裂纹最深点和裂纹末端的应力强度因子修正系数的计算结果和BS7910中T型节点表面裂纹公式计算结果对比如图4所示，左图为最深点，右图为裂纹末端。

图3 裂纹细部网格Fig.3 Crack meshes

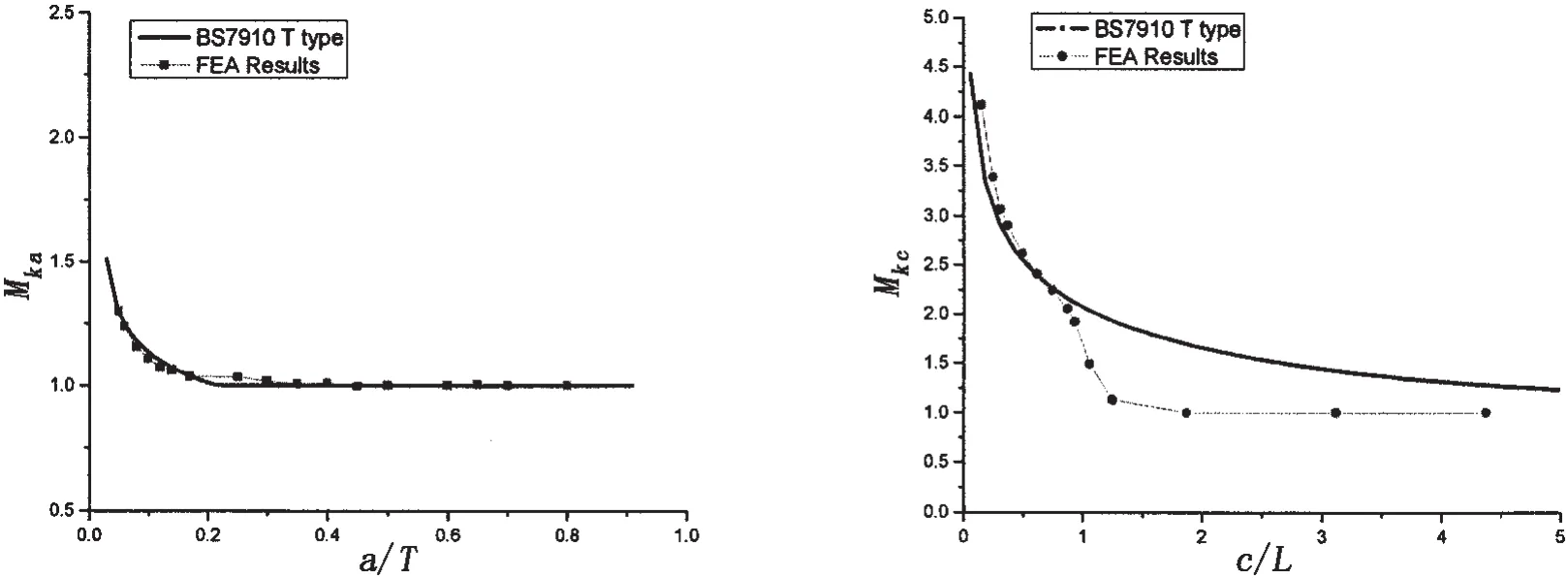
图4 应力强度因子修正系数对比Fig.4 Comparison of SIF magnification factors

在裂纹最深点，修正系数表示为裂纹深度和板厚比值a/T的关系；而在裂纹末端，将修正系数表示为裂纹半长和趾端半长之比c/L的关系，这样处理更容易观察到表面应力强度因子修正系数受趾端影响的变化规律。

在裂纹最深点，两种方法的计算结果很接近，实际上，从BS7910推荐公式的计算结果可以观察到，在裂纹深度较小时，裂纹最深点的应力强度因子修正系数就达到1（将小于1的结果都取为1），焊趾宽度对最深点的影响不大。因而在计算表面裂纹最深点应力强度因子修正系数时可以直接采用BS7910公式或者韩芸简化公式。在裂纹末端，裂纹长度较短时，两种方法的计算结果很接近，有限元计算结果略小。注意到有限元的计算结果，当c/L在接近及超过1的范围内时（L为焊趾端半宽，见图1），Mkc迅速减小，直到为1。这可以解释为当裂纹长度接近及超过焊趾范围时，几何形状导致的应力集中逐渐减小，从而使得修正系数减小。拟合裂纹末端有限元计算数据，得到Mkc的表达式。

4 船舶趾端表面裂纹疲劳扩展实例分析

计算实例为某客滚船180号肋位内底板与舷侧的肘板连接处趾端的疲劳寿命。

4.1 疲劳载荷

目前，宏观层次上的疲劳分析方法主要有基于S-N曲线和线性累计损伤理论的疲劳分析方法和基于裂纹扩展理论的断裂力学方法。相比于S-N曲线法，断裂力学方法可以更好地反映尺度效应和载荷次序效应，并可以更精确地计算已存在裂纹的结构的疲劳寿命。

疲劳载荷是根据对某客滚船整船有限元分析和对180号肋位内底板与舷侧的肘板连接处趾端的局部应力分析得到名义应力幅，并假定疲劳载荷的长期应力幅值的分布服从Weibull分布。概率分布函数为:

形状参数h对疲劳寿命的影响很大，取决于船的棱形系数。形状参数的取值一般在0.7-1.3之间，通过某一海况资料对一类船舶的疲劳载荷长期分析，用Weibull分布公式拟合得到。在各船级社中都给出了相应的形状参数的计算方法，可以通过实船参数计算得到[12]。本算例目标船在180号肋位内底板与舷侧的肘板连接处h=1.112。在形状参数值已知的情况下，尺度参数q可以通过形状参数和参考应力范围Δσ0得到。参考应力范围Δσ0，是n0次应力循环中仅出现一次的最大许用缺口应力范围，或者说超越概率为1/n0的参考应力范围。按DNV[12]的疲劳分析设计波法n0=104。

由（7）式在Matlab中生成0.75×108个应力比R=-1，平均应力σm=0的应力幅值伪随机数，即得到服从应力幅值的长期分布服从Weibull分布函数式（7）的0.75×108个循环组成的载荷谱。该载荷谱片段如图 5（a）所示，概率分布如图 5（b）所示。

表2 形状参数及尺度参数Tab.2 Shape parameter and scale parameter

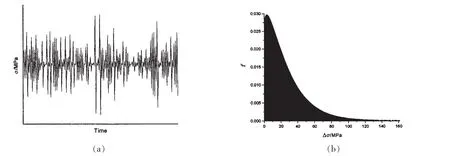
图5 服从weibull分布的载荷随机数据分布图Fig.5 Random loading series obey the Weibull distribution

4.2 裂纹扩展率曲线材料常数

黄小平等[13]将BS7910中推荐的裂纹扩展率表达式和收集到的大量的实验数据表示成da/dN～ΔKE曲线后，裂纹扩展率数据集中分布在R=0的裂纹扩展率曲线周围。因而对大多数结构钢，在无实测数据的情况下，推荐使用的单一裂纹扩展率曲线模型材料常数表示为:

4.3 焊接残余应力

对于平行于焊缝的表面裂纹，需要考虑垂直于裂纹面的焊接残余应力的影响。垂直于焊缝方向的残余应力在焊趾内、外表面的推荐取值为[14]:σR=0.2-0.（）3 σy，其中σy为材料的屈服极限。在计算由残余应力引起的应力强度因子时，从保守的角度考虑，可以认为残余应力沿壁厚均匀分布，并且等于表面处的残余应力。表面处的残余应力取为σR=0.3σy，取目标船180号肋位内底板与舷侧的肘板材料的屈服极限σy=345 MPa。应力比由下式计算。

4.4 疲劳裂纹扩展计算结果

基于单一曲线模型对某客滚船180号肋位内底板与舷侧的肘板连接处进行疲劳分析。肘板厚度为t=12 mm，底板厚度为T=20 mm。应力强度因子采用（4）式计算。深度方向的应力强度因子修正系数采用BS7910中T型接头焊趾表面裂纹应力强度因子计算公式，作为对比，裂纹末端应力强度因子修正系数的计算采用两种方法:（1）BS7910中T型接头表面裂纹应力强度因子修正系数计算公式；（2）采用拟合公式（6）计算。取初始裂纹深度a0=0.3 mm，初始裂纹半长c0=1.5 mm。根据前面所述方法得到的应力强度因子幅系列，裂纹扩展率曲线方程计算趾端表面裂纹沿深度方向扩展和沿长度方向的扩展。用两种应力强度因子计算方法计算得到的趾端表面裂纹沿深度方向的扩展曲线和沿裂纹长度方向的扩展曲线对比如图6和7所示。

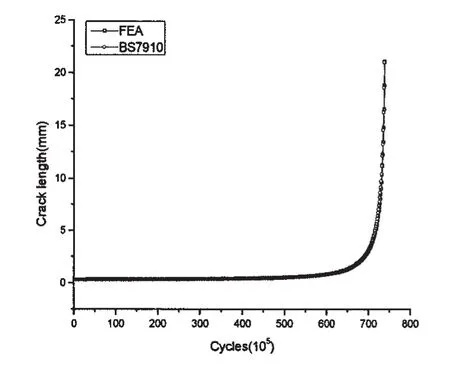
图6 裂纹深度方向扩展对比Fig.6 Comparison of crack growth curves at the deepest point

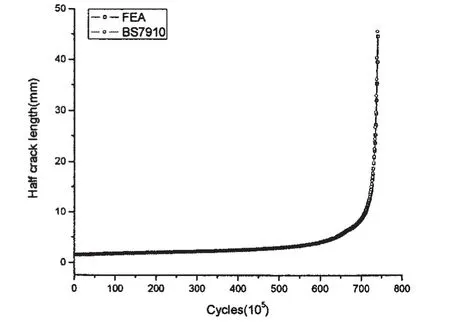
图7 裂纹长度方向扩展对比Fig.7 Comparison of crack growth curves at crack end on surface

只考虑表面裂纹的扩展，因而逐周计算到裂纹穿透板厚为止。两种计算方法得到的疲劳寿命均约为0.73×108，满足设计寿命0.5×108的要求。同时可以观察到，当裂纹长度较小时，裂纹扩展缓慢，裂纹扩展至一定深度和长度时，扩展速度会加快。当裂纹接近穿透板厚时，整个结构也就接近失效。已有裂纹存在的结构若仍用传统的S-N曲线法进行疲劳分析，将无法得到准确的疲劳寿命。对于船舶与海洋工程结构物，基于断裂力学的疲劳分析方法是极其有意义的。

两种方法的计算结果很接近，裂纹长度超过趾端影响范围后，会有微小差异。达到相同裂纹长度时，拟合公式（6）的计算结果比BS7910推荐公式的计算结果稍大，两者差异大约在105周次，这与整个疲劳寿命相比可以忽略。这是由于裂纹长度较小时的扩展寿命占了疲劳寿命最主要的部分，两种方法最主要的差异体现在裂纹长度超过趾端范围后，而这个阶段裂纹长度较长，裂纹进入快速扩展，这个阶段的疲劳寿命相比整个寿命已经很小了，因而对疲劳寿命的影响可以忽略。故建议在基于断裂力学方法计算类似结构的疲劳寿命时，将趾端放大系数的计算方法与对接接头、T型接头和十字接头的计算方法进行统一，即趾端表面裂纹应力强度因子放大系数可采用BS7910中的T型接头焊趾表面裂纹应力强度因子计算公式计算。

5 结 语

采用三维有限元计算，分析了肘板趾端表面裂纹应力强度因子修正系数随裂纹尺寸的变化规律。采用单一曲线模型和船舶疲劳载荷长期分布服从Weibull分布对某客滚船肘板—内底板结构的疲劳寿命进行了分析，得到如下结论:

（1）肘板趾端处半椭圆表面裂纹的应力强度因子可以采用Newman-Raju公式引入适当的修正系数计算得到，和T型接头焊趾表面裂纹应力强度因子相比趾端表面裂纹应力强度因子沿深度方向的放大系数和T型节点相差很小，而表面端点应力强度因子修正系数则当裂纹长度在肘板厚度范围内时和T型节点相差很小，超出后则相差较大。

（2）采用裂纹扩展率单一曲线模型对某客滚船局部结构疲劳寿命进行计算，该结构的疲劳寿命满足设计寿命要求。

（3）趾端表面裂纹采用三维有限元计算结果和BS7910中T型节点表面裂纹应力强度因子计算结果得到的疲劳寿命差异甚微，故建议在基于断裂力学方法计算类似结构的疲劳寿命时，可将T型接头焊趾表面裂纹应力强度因子的计算方法用于趾端表面裂纹应力强度因子的计算。

[1]韩 芸,黄小平,崔维成,胡 勇.T型接头焊趾表面裂纹应力强度因子的简化计算方法[J].中国造船,2006,47:1-11.

[2]Bowness D,Lee M M K.Prediction of weld toe magnification factors for semi-elliptical cracks in T-butt joint[J].International Journal of Fatigue,2000,22:369-387.

[3]BS7910.Guide on Methods for Assessing the Acceptability of Flows in Structures[S].British Standards Institution,1999.

[4]Newman J C,Raju I S.An empirical stress-intensity factor equation for the surface crack[J].Engng Fract Mech,1981,15:185-192.

[5]Okawa T,Sumi Y,Mohri M.Simulation-based fatigue crack management of ship structure details applied to longitudinal and transverse connections[J].Marine Structure,2006,19:217-240.

[6]Dexter R J,Pilarski P J.Crack propagation in welded stiffened panels[J].Journal of Constructional Steel Research,2002,58:1081-1102.

[7]Jang Beom-Seon,Ito Hisashi,Kim Kyung-Su.A study of fatigue crack propagation at a web stiffener on a longitudinal stiffener[J].Journal of Marine Science Technology,2010,15:176-189.

[8]Huang X P,Moan T,Cui W C.An engineering model of fatigue crack growth under variable amplitude loading[J].International Journal of Fatigue,2008,30:2-10.

[9]施 伟,黄小平,崔维成.基于疲劳裂纹扩展率单一曲线模型的疲劳寿命预测[J].船舶力学,2008,12(2):264-271.Shi Wei,Huang Xiaoping,Cui Weicheng.Fatigue crack growth prediction based on unique crack growth rate curve model[J].Journal of Ship Mechanics,2008,12(2):264-271.

[10]刘 强,王 芳,黄小平,崔维成.裂纹尖端塑性区三维有限元分析[J].船舶力学,2006,10(5):90-99.Liu Qiang,Wang Fang,et al.Three dimensional FE analysis of the plastic zone size near the crack tip[J].Journal of Ship Mechnics,2006,10(5):90-99.

[11]徐晓冬,黄小平,崔维成.大型客滚船结构细部疲劳强度分析[J].中国造船,2010,51:35-46.

[12]Det Norske Veritas.Fatigue assessment of ship structures[S].Det Norske Veritas Class Notes No.30.7,2003.

[13]黄小平,贾贵磊,崔维成,祁恩荣.海洋钢结构疲劳裂纹扩展预报单一曲线模型[J].船舶力学,2011,15(1-2):118-125.Huang Xiaoping,Jia Guilei,Cui Weicheng,et al.Unique crack growth rate curve model for fatigue life prediction of marine steel structure[J].Jouranl of Ship Mechanics,2011,15(1-2):118-125.

[14]黄小平.高强度钢潜艇锥柱焊接结构的疲劳性能研究[D].哈尔滨:哈尔滨工程大学,2001.

[15]钱 怡,崔维成.变幅载荷下疲劳裂纹扩展规律试验研究综述[J].船舶力学,2010,14(5):556-565.Qian Yi,Cui Weicheng.An overview on experimental investigation on variable amplitude fatigue crack growth rule[J].Journal of Ship Mechanics,2010,14(5):556-565.

[16]王一飞,衣高洁,黄小平,崔维成.疲劳裂纹扩展中表征裂纹闭合水平参数的确定[J].中国造船,2008,49:45-51.

[17]黄小平,韩 芸,崔维成等.变幅载荷作用下焊接接头疲劳寿命预测方法[J].船舶力学,2005,9(1):89-97.Huang Xiaoping,Han Yun,Cui Weicheng,et al.Fatigue life prediction of weld-joints under variable amplitude fatigue loads[J].Journal of Ship Mechanics,2005,9(1):89-91.

[18]Han Yun,Huang Xiaoping,Zhang Yi,Cui Weicheng.A comparative study of simplified SIF calculation of surface cracks at weld toe[J].Journal of Ship Mechanics,2005,9:87-96.

[19]Huang X P,Zhang J B,Cui W C,Leng J X.Fatigue crack growth with overload under spectrum loading[J].Theoretical and Applied Fracture Mechanics,2005,44:105-115.

[20]Lee E U,Glinka G,Vasudevan A K,Iyyer N,Phan N D.Fatigue of 7075-T651 aluminum alloy under constant and variable amplitude loadings[J].International Journal of Fatigue,2009,31:1858-1864.

[21]Newman Jr J C,Brot A,Matias C.Crack-growth caculations in 7075-T7351 aluminum alloy under various load spectra using an improved crack-closure model[J].Engineering Fracture Mechanics,2004,71:2347-2363.

[22]Taheri F,Trask D,Pegg N.Experimental and analytical investigation of fatigue characteristics of 350WT steel under constant and variable amplitude loading[J].Marine Structures,2003,16:69-91.

[23]周 驰,崔维成.用现有疲劳试验数据确定疲劳裂纹扩展率[J].中国造船,2003,44:74-79.