沪深股市指数收益率波动性的实证分析

冷 军

0 引言

随着全球经济一体化的进程，我国股市也越来越因为对全球经济的敏感反应而呈现出不稳定和风险。尤其是2008年以来，金融危机席卷全球，使全球经济迅速下滑，全球主要股市均出现了异常的波动，各个国家都把金融风险管理放到了极其重要的位置。股指收益率的波动性可以作为一种度量金融风险的手段。因此，对我国沪深股票市场股指收益率的波动性的研究，在理论和现实两方面均具有十分重要的意义。已有的研究主要是基于收益率残差分布服从条件正态分布对我国股票市场收益率进行实证分析。本文基于广义误差分布（GED），利用GARCH族模型，选取了1995年至2011年近16年的数据，对我国股票市场的收益率波动性进行长期的分析。本文通过实证分析发现采用广义误差分布时（GED），GARCH模型对我国股票市场的收益率波动性拟合的更好。

1 研究方法

ARCH模型已被广泛地认为是目前最能集中地反映方差变化特点的模型，因而在经济时间序列的分析中得到了广泛应用。在恩格尔的ARCH模型基础上，又有其他学者提出了GARCH、EGARCH、CGARCH以及GARCH-M等改进模型（一般合成为GARCH族模型），因其各自具有不同的特性，本文运用这些模型从不同的视角揭示我国股票市场指数收益率的波动性状况。

2 数据描述及检验

2.1 数据描述

本文以上证综合指数和深圳综合指数为代表，研究我国股票市场指数收益率波动性特征。尽管上海交易所从1990年12月开始发布上证综合指数，深圳交易所从1991年4月开始发布深证综合指数，但是由于我国1995年5月1日开始实行5天工作日制，因此，我国股市交易也从1995年5月2日开始由一周6个交易日改为一周5个交易日，因此，为了时间序列的周期一致，本文选取1995年5月2日至2011年2月28日间每一交易日的日收盘价作为样本，共3839个交易数据（数据来源于大智慧软件），构成的时间序列分别为{SHP}和{SZP},对我A国股票市场近十六来的运行状况进行研究。在这一样本期内，我国股市经历了2001年至2005年长达4年的熊市，2005年至2007年的大牛市以及之后持续的熊市；同样，也经历了我国股市国有股减持即股权分置改革，以及2008年以来的席卷全球的金融危机。因此，基于这么长的样本期来对我国沪深两地股市指数收益率的波动性进行研究，具有较好的代表性。图1为样本期内上证综指和深圳综指的走势图。

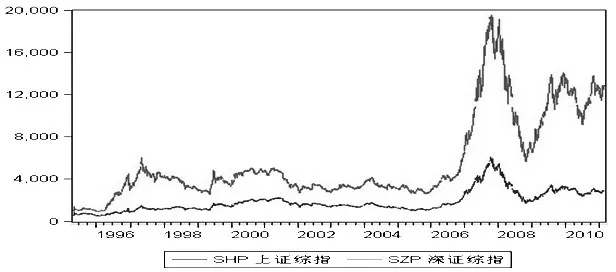
图1 1995.5至2011.2上证综指和深证综指走势

股市日收益率采用股价指数的一个对数差分来衡量，设Pt为当天的收盘指数，Pt-1为前一天市场的收盘指数，则可以将股票指数的收益率为：

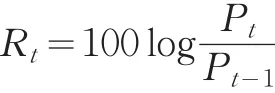
根据上述公式，在沪深综指时间序列分别为{SHP}和{SZP}的基础上，构建了分表代表沪深两地综指日收益率的时间序列{SHR}和{SZR}。图2为上证综指和深圳综指日收益率走势图。从图中可以看出，上证综指和深证综指的收益率的波动都表现出明显的时变性、突发性、与集聚性特征。

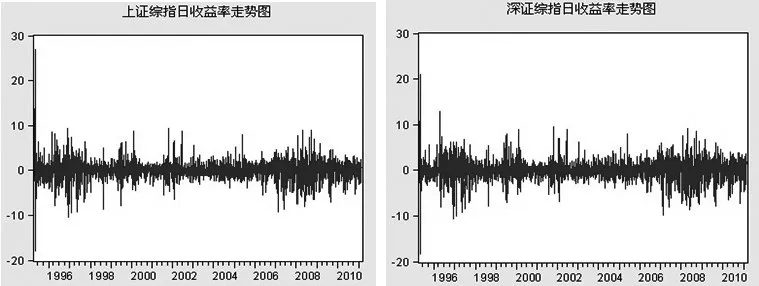
图2 上证综指和深圳综指日收益率走势图

2.2 正态性检验

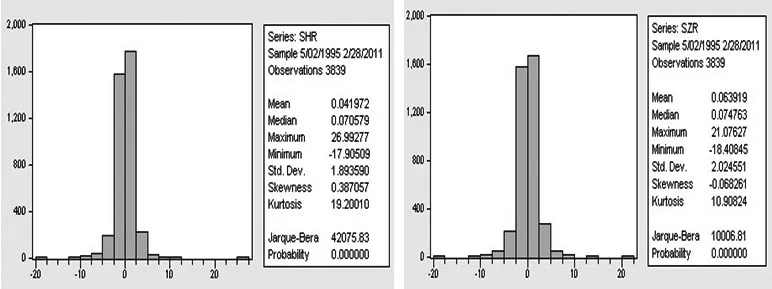
图3 沪深综指收益率的数据特征（左图为沪市，右图为深市）

通过eviews对上证综指日收益率时间序列和深证综指日收益率时间序列分别做描述性统计。获得如图3所示的两指数日收益率的直方图。由图3可知，上证综指收益率从的平均（Mean）小于深证综指收益率，偏度（Skewness）和峰度（Kurtosis）都大于深证综指收益率，另外，两地股市的JB统计量均非常大且其P为0.00000。由于对称分布的偏度等于0，而上证综指收益率的偏度是正值，说明上海股市的收益率是向右偏斜的，而深证综指收益率的偏度是负值，说明是向左偏斜的。正态分布的峰度等于3，而沪深两地股市的综指收益率的峰度均远远大于3，表明沪深两地股市的收益率均显著不服从正态分布，且具有较为明显的“尖峰厚尾”。

2.3 平稳性检验

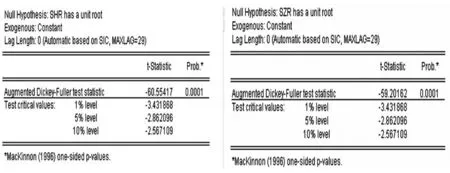
图4 上证综指日收益率序列{SHR}（左）和深证综指日收益率序列{SZR}（右）的ADF检验

对上证综指日收益率序列{SHR}做ADF检验，如上图4所示，所得检验统计量为-60.55417，伴随概率为0.0001，且1%显著性水平下的MacKinnon临界值为-3.431868，因此拒绝序列存在单位根的假设，该序列是平稳序列。同样可验证深证综指日收益率序列{SZR}序列也是平稳序列。

3 实证结果及分析

根据序列的自相关和偏自相关分析图，上证综指日收益率序列{shr}存在滞后11阶偏自相关，而深证综指日收益序列{szr}存在滞后15阶偏自相关，又根据简单实用原则，均值方程分别设为

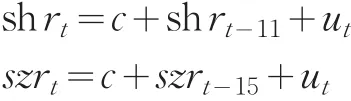
下面根据方差方程的设定不同，采用不同的模型对我国沪深股市综指日收益率的波动性进行研究，模型参数估计方法采用拟极大似然估计法，得到稳健标准差。

3.1 GARCH(1,1)模型

模型各参数估计结果见表1。

表1 沪深股市收益率GARCH(1,1)模型估计结果

从表1可知，沪深股市尾部厚度的度量参赛ν的估计值分别是1.177346和1.257805，均小于2，且随行概率均非常低，说明收益率不具有正态分布（正态分布ν=2）的特性，呈现出后尾性，GED分布拟合数据效果良好。上海股市和深圳股市的方差方程中残差平方项的系数α1和方差项的系数β1均是正数，且在0.001水平上显著，反映了异方差性和波动聚集性的存在；而系数之和α1+β1均接近于1，则说明了两市股价具有很强的波动持续性。对两地股市的方差方程系数和进行Wald检验结果如表2：

表2 两地股市方差方程系数和的wald检验

由沪深两地股市指数收益率方差方程系数和的wald检验结果可知，由于F检验和卡方检验的随行概率均大于显著性水平，因此接受系数和为1的原假设，表明波动性冲击具有持久性的效应，且过去的冲击对未来波动的影响衰减得十分缓慢。另外，通过对残差项进行ARCH-LM检验，发现不存在ARCH效应，因此利用GARCH(1,1)模型描述沪深股市指数收益率波动的效果较好。

3.2 基于GJR-GRACH(1,1)模型的杠杆效应研究

GJR-GRACH(1,1)的方差形式为：

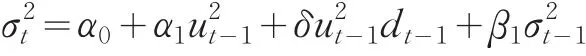
模型各参数估计结果见表3。

表3 沪深股市收益率GJR-GRACH(1,1)模型估计结果

由估计结果可知，上海股市综指收益率的δ在5%的水平上显著，而深圳股市综指收益率的δ并不是不显著的，表明在样本期内上海股市的杠杆效应明显，而深圳股票市场的杠杆效应不十分明显。但两市场的δ都为正，说明利空消息影响大于利好消息影响。

3.3 E-GARCH（Exponential GARCH）模型

为进一步验证杠杆效应，用EGARCH（1，1）模型做实证检验，结果如下表4所示：

表4 沪深股市收益率利用E-GARCH(1,1)模型的估计结果

由表4可知，沪深两地股市综指收益率的非对称系数γ均为负，说明利空消息比利好消息产生更大的波动，其中，上海股市在5%的水平上显著，深圳股市不显著。上海股市，γ=-0.024560，则正的冲击对波动的影响比负的冲击对波动的影响小，当ut-1＞0时，有一个α1+γ=0.201151倍冲击，当ut-1＜0时，有一个α1+γ=0.250271倍的冲击。且参数统计量均显著，说明对利好和利空消息对股价波动性影响较大。 α1和 β1都很显著，但 α1+β1＞1，表明收益率波动不会衰减，波动最为剧烈，不满足平稳性条件。

3.4 GARCH-M模型

表5 沪深股市收益率利用GARCH-M(1,1)模型的估计结果

由表5可知，上海市场的风险溢价系数θ为-0.015935，且在10%的水平上显著，符号为负，说明上海股市的投资者的收益期望与市场波动之间呈弱负相关，但绝对值很小，投资者对市场风险是弱偏好的，有一定的投机成分，这从另一个侧面反映了我国股票市场仍是一个不成熟的新兴资本市场，股票市场中仍有一定的投机现象，而这种投机性的存在又会使得股票价格的波动更加剧烈。另一方面，深圳市场的风险溢价系数θ为0.028534，符号为正，说明收益率与风险成正向变化，投资者对市场风险是厌恶，对于波动需要一定的风险补偿，但绝对值也很小，仅为0.080027，说明风险厌恶程度很小，市场的投机现象没有沪市的严重。

4 结论

本文根据不同模型的特点，分别采用GARCH模型族中 的 GARCH(1,1)、GJR-GRACH(1,1)、EGARCH(1,1)以 及GARCH(1,1)-M等模型，从多个视角我国股票市场指数收益率的波动性状况进行分析。实证研究结果表明：

（1）和发达国家的股票市场一样，我国股票市场指数收益率也存在着波动的聚集性、爆发性、持久性以及均值恢复性。

（2）我国上证指数收益率波动性存在明显的非对称性，杠杆效应明显，利好和利空消息的发布对股票市场指数收益率的波动性会显著的影响。这与朱均均、谢识予（2011）、周少甫（2005）的研究结果基本一致。而深证指数收益率的非对称性、杠杆效应均不显著，利好和利空消息对股指收益率的波动性影响不显著。这与周少甫（2005）发现的沪深两市均具有显著的非对称性的研究结果有所不同。

（3）我国沪深股票市场总体上不存在显著的风险——收益权衡关系，投资者总体上趋于中性，其中上海市场投资者有点风险弱偏好，深圳市场有一定的风险厌恶，对承担风险要求一定的补偿。这与周少甫（2005）、陈雄兵、张宗成（2008）的研究结果有所不同，但在沪市中的投机性要比深市严重的结果与周少甫（2005）的结论一致。这意味着我国股票市场虽然与发达国家股市之间虽然仍存在比较大的差距，但已有很大的改善，投机现象有所减少。

[1]藩越.成交量的GARCH修正模型在股市波动中的应用[J].统计与决策,2004,(8).

[2]周少甫,袁兴兴.我国股票市场波动非对称性的实证研究[J].当代经济管理,2005,（6）.

[3]陈雄兵,张宗成.基于修正GARCH模型的中国股市收益率与波动周内效应实证研究[J].中国管理科学,2008,(8).

[4]高铁梅.计量经济分析方法与建模（第二版）[M].北京:清华大学出版社,2009,(5).

[5]陈守东,马辉,才元.上海证券市场分阶段收益率与波动性的特征分析[J].吉林大学学报(社会科学版),2006,(7).

[6]中国股市波动率的双重不对称性及其解释——基于MS-TGARCH模型的MCMC估计和分析[J].金融研究,2011,(3).

[7]马慧敏.沪市A股弱势有效性实证研究[J].求索，2011，（8）.