论聚类分析中聚类标准化与正交化的必要性

杜子芳，刘亚文，徐一丁

聚类分析是三大多元统计分析方法之一，在许多领域都有广泛的应用，聚类分析不仅表现活跃，而且分支众多。首先有样品聚类与变量聚类之分，其中样品聚类又有面向大样本量情形的快速聚类与面向样本量不大情形的常规聚类两个分支。对于这其中的常规聚类，还可细分为有序样品聚类与非有序样品聚类，而对于非有序样品聚类，有聚类类数由少而多的分解法与由多而少的归并法的区别。归并法最为常用，也称谱系聚类。

聚类家族人丁兴旺，其共同的基因可以归纳为两个：一是“模型”限于处理数值型变量尤其是非离散变量；二是“模型”的基础除变量聚类少数场合外其余概为距离计算。不妨回顾一下聚类分析的过程与细节，容易知道无论是谱系聚类还是快速聚类，任何场合的距离计算不外乎三种：样品之间的距离、样品到类的距离以及类与类之间的距离。而这些计算的唯一依据是样品之间的距离，简称样品间距，只有谱系聚类的ward方法例外。

距离首先是一个几何概念，其中最为人熟悉的是二维和三维几何空间的欧几里德距离。在其后的发展中，距离在维数、幂次数等方面被推广了，距离被抽象为满足下列性质的一个函数族：（1）非负性；（2）对称性；（3）三角可加性。

值得提醒人们特别关注的是，三角可加性虽然是一种特殊的可加性，但毕竟还是可加性，而可加性意味着几何距离中向量的各分量量纲必须一致；至于可加性前面要加上“三角”做修饰，则意味着几何距离中向量的各分量在笛卡尔坐标系里必须正交。这是几何距离定义中所隐含的两个重要特性。

样品间距完全脱胎于几何中的距离概念，这是毋庸置疑的，但样品间距在几何距离隐含的上述两个关键特性上或许是被人们有意或许是不经意地被模糊了。假如询问学过回归分析的学生，需要进行多重共线性的诊断吗？回答肯定的。而假如询问学过聚类分析的学生，聚类分析需要进行量纲不一致和变量不正交的诊断吗？回答“是”的恐属凤毛麟角。还有一个明证是统计软件的聚类分析程序中既无量纲一致和变量正交化的独立模块，在内容相关的模块里，缺省设置也不是能使量纲一致和变量正交化的手段选项。在迄今所见的文献中未见任何有关主题研究的文献。

被人们有意或许是不经意地被模糊的两个关键特性，一是几何距离中向量的各分量量纲是一致的，故各分量的量值是可加的，可样品距离中各个变量许多场合量纲并非一致。多元统计分析中关于消除量纲的方法是比较丰富的，主要有标准化变换、极差标准化变换和极差规格化变换三种。但人们往往将这些方法与中心化变换和对数变换之类变换方法并列，且对三种消除量纲影响的方法孰优孰劣只字不提，其结果是量纲一致化的必要性被严重地淡化了，以致聚类分析里完全缺少判别分析那种将马氏距离作为距离判别唯一选项的明快。

何况，若记两个p维样品x=[x1,…,xp]′和 y=[y1,…,yp]′之间的欧氏距离为：

而相同的两个p维样品之间的统计距离或马氏距离为：

q其中S为样本协方差矩阵，则正如Richard A.Johnson和Dean W.Wichern所说：“但是，没有关于不同类的先验知识。这些样本量就无法计算。由于这个原因，在聚类问题中更倾向于采用欧氏距离”。也就是说，由于“类”在聚类开始的阶段尚不存在，类内的方差S无从谈起，所以欧氏距离就替代了似乎更合理的统计距离或马氏距离。

被人们有意或许是不经意地被模糊两个关键特性之二，是几何距离中向量的各分量在笛卡尔坐标系里都是正交的，而样品距离中各变量间往往存在一定程度的相关，很多场合不能满足正交条件，费歇尔感觉到了这一点，在与聚类分析关联紧密的姊妹方法判别分析中提出了著名的费歇尔变换。费歇尔变换是一种正交变换，可以很好解决不同变量不正交的问题。可惜的是，迄今并未有人尝试将此移植到聚类分析。当然有必要指出的是，即使移植了，量纲一致及可加性的要求并不能因此获得满足。

样品间距迄今存在的量纲不一致和变量不正交这两个固有缺陷，第一个缺陷量纲不一致无法真正消除，例如试图将血压与身高的量纲差异消除的努力在科学的范畴里恐怕永远不会成功。通过标准化进行矫正也许是人们能够想到的理想方法，只有规格化可能与其相比。第二个缺陷变量不正交或变量间存在相关性，假如不考虑量纲不一致的影响，其实完全可以真正消除，而且矫正的手段非常简单：正交化。有些多元统计分析教科书非常重视变量不正交或变量相关性问题，并提供了马氏距离、斜交空间距离两种解决方法，但也未明确宣示正交化不可或缺的必要性。

本文的主旨在于研究两个问题，一是从聚类分析结果(取决于样品间距)看，是否有必要进行正交化矫正；二是假如需要，那么应该如何进行正交化。

对于第一个问题，可以通过证伪的方法轻易得到解决。本文选取两个熟悉度很高的且各变量量纲可以看作相同的案例，按未正交化的一般方法计算样品距离阵，再按正交化的方法重新计算距离阵，正交化的方法是对 p个变量求主成分，模型为：

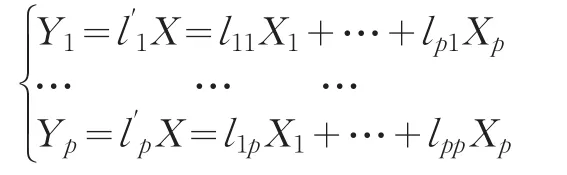
这样得到的各主成分是相互正交的，即

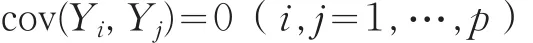
以各主成分的值Y1,…,Yp作为新的变量，重新计算距离。

计算比对两种结果。由于聚类分析的原理是先将样品距离小的样品聚在一起，因此距离的绝对数没有实际意义，本文主要通过比较距离的大小和排序（秩）来比对两种距离。比对的具体做法是：

（1）如果有n个样品，则可得到原始距离和正交后距离各C2n个。将两个距离矩阵分别按列排成C2n维的向量，分别求两个向量的秩xi，yi(i=1,…,C2n)，计算两种方法的距离之间的斯皮尔曼相关系数rd：

其中，di=xi-yi，m为距离向量维数。

假如不正交不影响样品间距的顺序和聚类分析结果，两者应该正相关，且斯皮尔曼相关系数rd为1，因此1-rd可以视为两者差异大小的一个量度。

（2）比较两种距离的秩xi，yi的差异。如果正交不影响样品间距的顺序和聚类分析结果，那么两种应该是完全一致的。

（3）按照矩阵先行后列的顺序计算样品间距，将两种方法计算的样品间距的大小顺序进行比较。若正交不影响样品间距的顺序和聚类分析结果，那么样品间距的大小顺序应该是一致的。例如，不正交计算的样品间距d1,2大于d3,5，若正交不影响样品间距的顺序和聚类分析结果，那么正交化变换后的样品间距d1,2也应该大于d3,5。

这里引入逆序对（different ordered pair）的概念来进行比较。设原始距离秩为向量x，正交后的距离秩为向量y，第i个距离秩为(xi,yi)，第 j个距离秩为(xi,yi)，i,j=1,…C2n,如果 xi＞xj，而 yi＜yj；或者 xi＜xj，而yi＞yj，则称i和 j是逆序对，逆序对只要求x变化方向和y变化方向相反，并不要求i和j中x的变化量|xi-xj|与y的变化量|xi-xj|相等。

类似的，同序对（same ordered pair）的概念为如果xi＞xj，且 yi＞yj；或者 xi＜xj，而 yi＜yj，则称 i和 j是同序对。另外，若i和 j，有 xi=xj或 yi=yj的情况，则i和 j是同分对（tied pair）。

若原始距离和正交后的距离各C2n个，则可计算出逆序对、同序对、同分对的个数共个，计算逆序对的比例可以衡量两种距离差异大小。

例1：鸢尾花数据

鉴于全部150个样品的样品间距阵的元素总数为149*75，过于冗长，既不容易突出问题也不便于表达，为此只随机选出10个样品（表1）的计算结果列在表2中，这样足以清晰地反映问题的实质所在。

表1 随机抽取的10个样品

（1）依斯皮尔曼相关系数得到两者的套算差异率为9.53%；（2）按间距顺序变化情况衡量，45个间距中正交与

表2 随机抽取的10个样品间距

否未产生影响的有8个，未正交排序后移的有23个，前移的有14个。（3）两者存在明显差异以致顺序颠倒的也不鲜见，如表中带阴影的3对6个样品即是如此，此即为逆序对。45个间距计算出的逆序对、同序对、同分对见表3。

表3 逆序对、同序对、同分对个数

例2：头盖骨数据

针对32个头盖骨样品数据计算的（1）斯皮尔曼系数为97.9%，两者的套算差异率为2.1%；（2）按间距顺序变化情况衡量，496个间距中正交与否未产生影响的有12个，正交排序后移的有266个，前移的有218个。（3）496个间距计算出的逆序对、同序对、同分对见表4。

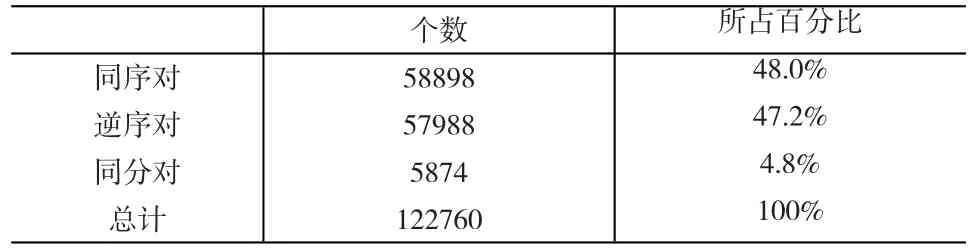
表4 逆序对、同序对、同分对个数

两个例子的比对结果表明，不仅未正交化与正交化的两种样品间距自身的数值不同，而且样品间距的大小顺序也存在明显的差异。

尽管表中所展示的只是不正交与采用主成分法正交化的两者的样品间距顺序发生变化的结果，但由于这种顺序变化必然导致聚类分析结果产生差异，所以进行正交化矫正完全是有必要的。

那么应该如何进行正交化呢？关于正交化的实施途径有许多现成方案可供选择，最直接两个正交化方法——主成分分析与格兰姆—施密特方法。前者与聚类分析同属多元统计分析；后者较少统计色彩但更具一般性。

主成分的正交方法前文已述，格兰姆—施密特方法具体计算方法为：

先取Y1=X1，然后令Y2=X2-h21Y1使(Y2,Y1)=0，即选h21使(X2-h21Y1,Y1)=0，即h21=(X2,Y1)/(Y1,Y1)，再令Y3=X3-h32X2-h31X1使 (Y3,Y2)=(Y3,Y1)=0，定出系数h32,h31；一般地，令

Yi=Xi-hi(i-1)Yi-1-…-hi1Y1使(Yi,Yi-1)=(Yi,Yi-1)=…=(Yi,Y1)=0，这样就可以求出一组两两正交的向量。

有必要指出的是：虽然施密特正交化方法似乎因更具一般性而容易令人产生其统计色彩比较淡些的印象，从而会使人们忽视格兰姆——施密特正交化方法在统计分析中的作用。格兰姆——施密特正交化方法不同于主成分的最重要的地方在于，主成分变换是粉碎性的，变换后原有变量几乎面目全非（除非再进行因子旋转），而格兰姆——施密特正交化方法是将原有变量中一个原封不动予以保留，以此作为变换的主轴。正如格兰姆——施密特正交化方法在统计学中受到忽视一样，这一点也是容易被视为当然如此而最终滑过人们的视野。其实，正是这微不足道的一点，在统计中可能甚为有用。例如可将某个最重要的变量作为主轴予以保留，这样至少可以部分达到因子旋转的目标，一定程度上减少主成分难以解释之弊。

以上几种方式都是普通的或成熟的正交化方法，不必怀疑是否能够达成我们的初衷。疑问也许在于，依据这几种方法计算的样品距离与马氏距离和斜交空间距离是否具有一致性，会不会因不具一致性导致据此进行的聚类结果也不一致。使用上面提到的两个案例，计算结果发现，格兰姆——施密特方法与主成分分析的结果完全一致，并无例外。这在理论上也是有根据的。对一个向量空间而言，标准正交基的变换相当于坐标轴的平移与旋转，平移对距离没有任何影响，而压缩与膨胀都是线性的和成比例的，会改变距离的大小而不会改变距离的顺序。

另外，格兰姆——施密特方法和主成分分析与马氏距离和斜交空间距离的结果（指距离的顺序）也是完全一致的。因而我们需要决定的是，究竟应优先考虑哪种方法为好；或者说各有千秋，只是场合不同。

单从公式或表达方式看，马氏距离最为简单，且与统计渊源最深，既然效果一样，似乎应优先选择。有些文献对马氏距离的指责系因马氏距离不具穿透性，即样品间距的结果无法用于样品与类之间的距离。斜交空间距离比马氏距离比较复杂，但具有所谓穿透性，即可兼顾样品间距与样品与类之间的距离。相比之下，格兰姆——施密特方法和主成分分析明显要复杂很多，看似必定出局。然而，公式或表达方式的复杂不等于计算复杂。事实上，格兰姆——施密特方法和主成分分析只是进行变量的正交化，并不直接涉及样品间距的计算。在其基础上的样品间距完全是独立进行的，允许多种选择。反观马氏距离和斜交空间距离，正交化与距离计算是融合进行的，总的计算量实际要大于施密特方法和主成分分析两种方法。因此，综合考虑聚类结果、总的计算量大小、统计学者的熟悉程度以及对样品与类之间距离的潜在影响，主成分分析是应该优先选择的。也就是说，正交化在程序中宜作为必选项而非普通备选项，而主成分分析应作为正交化的缺省设置。

不选择马氏距离或统计距离作为样品间距标准方法的理由还在于其为样品到类之间距离的广义距离构成中的一项，而这一项的协差阵是各类的而非总体的，换言之，如此要涉及两种意义不同的马氏距离计算，容易混淆，且实际计算量会增大。斜交空间距离与此相类似，无法避免广义距离计算中要重新计算马氏距离的浪费现象。与此相对照的是主成分分析，由于变量已经正交，各类马氏距离的计算过程变得非常简单，且不存在混淆的可能，当然应被视为最佳选择。格兰姆——施密特方法与主成分分析十分相似，唯一不足是与统计学的渊源不够。

尽管上述对于标准化或规格化以及正交化的讨论对于正确理解与应用聚类分析是有益的，然而我们必须指出，在相关领域，至少还有以下问题尚未解决：

（1）标准化或规格化使量纲一致化，只是在数学层面或形式上解决了问题，但无法使问题的实质有任何改变：一个随机变量标准化后的量纲实际上是该随机变量的标准差，不同随机变量标准化后的量纲只是形式上的相同，并非实质上的一样。

（2）主成分分析是在样本基础上进行的，如何解决其统计显著性问题。

笔者认为，这些问题的解决有助于改进聚类分析效果，并使聚类分析具有浓郁的统计学特色。

[1]Anderson,E.The Irises of the GaspéPeninsula[J].Bulletin of the American Iris Socity,1939，（59）.

[2]Efron,B.The Efficiency of Logistic Regression Compared to Normal Discriminant Analysis[J].Journal of the American Statistical Associa⁃tion,1975，(81).

[3]Lachenbruch,P.A.Discriminant Analysis[M].New York:Hafner Press,1975.

[4]Ganesalingam,S.Classification and Mixture Approaches to Clustering Via Maximum Likelihood[J].Applied Statistics,1989,(38).