缺失数据多重插补处理方法的算法实现

庞新生

在国外相当多的抽样调查中，对缺失值进行插补处理是非常普遍的，替换缺失数据技术的意义在于比列表删除浪费更少的信息，且当缺失数据为非随机缺失时，替换缺失数据技术比列表删除更稳健，特别是当数据收集者与数据分析者是不同的个体时，插补法更具优势。插补法主要经历了单一插补和多重插补两阶段，多重插补法的出现，弥补了单一插补法的缺陷，第一，多重插补过程产生多个中间插补值，可以利用插补值之间的变异反映无回答的不确定性，包括无回答原因已知情况下抽样的变异性和无回答原因不确定造成的变异性。第二，多重插补通过模拟缺失数据的分布，较好地保持变量之间的关系。第三，多重插补能给出衡量估计结果不确定性的大量信息，单一插补给出的估计结果则较为简单。与单一插补相比，多重插补唯一的缺点是需要做大量的工作来创建插补集并进行结果分析，无论是何种情况下的多重插补，其处理过程都是比较复杂的，新的统计计算方法的出现大大简化了计算并完成一系列简单的极大化或模拟。在缺失数据处理中，主要涉及的是数据添加算法，其中讨论最多的是EM算法和马尔科夫链蒙特卡洛方法(MCMC)。

1 EM方法在缺失数据多重插补处理中的实现

EM算法是Dempster，Laired和Rubin于1977年提出的求参数极大似然估计或最大后验估计的一种方法，通过假设潜在变量的存在，EM算法极大地简化了似然函数，从而解决了方程求解问题。

假设X是服从某一分布的观测数据集，Y为缺失数据，则有完全数据集Z=(X,Y)，则Z的密度函数为:

从式(1)可以看出，密度函数 p(z|θ)是由边缘密度函数p(x|θ)，缺失数据 y的假设，参数θ初始估计值及缺失数据与观测变量之间的关系决定的。由式(11)给出的密度函数可以定义完全数据似然函数:

由于缺失数据未知，因此似然函数L(θ|Z)是随机的，且由缺失数据Y所决定的。这里，我们假定存在缺失数据的变量 是随机缺失的（MAR），在此假定之下，可以保证似然估计的精度。

由于E步是在给定观测X和当前参数估计值，计算完全数据对数似然函数log p(X,Y|θ)关于缺失数据Y的期望，为此，定义对数似然函数的期望:

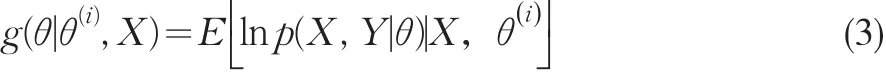
其中θ()i为已知的当前参数的估计值。

在式(3)中，X与θ()i为常数，θ为待优化的参数，Y为一随机变量，并假设它服从某一分布 fY()y:

定义函数:

h()θ,Y=Δln p(X,Y|θ)(5)因此，式(5)可写为:

其中f(y | X，θ(i))是缺失数据Y的边缘密度函数，并且依赖于观测数据和当前参数θ()i，D为 y的取值空间。由于有:

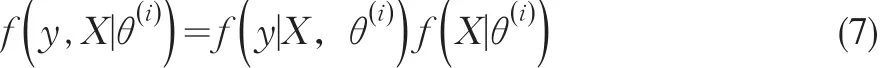
且因子 f(X |θ(i))与θ无关，所以在实际问题处理中，用f(y , X|θ(i))代替f(y | X，θ(i))不影响式(5)中似然函数的最优化。

EM算法的第二步M-step：最大化期望值 g(θ|θ(i),X)，即找到一个θ(i+1)，满足：

其中Θ代表参数空间。

EM算法是利用缺失数据和模型参数之间的迭代关系：如果缺失数据已知，模型参数未知，那么根据缺失数据就可以对模型参数进行估计。同样，如果模型参数已知，根据模型也可以得到缺失数据的估计。先在假定模型参数的基础上得到缺失数据的估计，然后再利用缺失值的估计值修正模型参数，这样不断地进行迭代，直至模型参数值收敛。EM算法的主要目的在于提供一个简单的迭代算法来计算极大似然估计，每一步迭代都能保证似然函数值增加，并且收敛到一个局部极大值，该算法的最大优点是简单和稳定，不足之处在于：第一，不同的模型需要不同的程序，不存在统一的处理程序；第二，当缺失数据比较多时，运算速度往往比较慢；第三，标准差只能在运算收敛后通过其他均值计算，无法直接获得。

2 MCMC方法在缺失数据多重插补处理中的实现

MCMC方法适合于处理多维非单调确定缺失目标变量多重插补，实践中，一般都是通过DA法实现对复杂分布的模拟，从而使得多重插补得以实施。MCMC方法是一组方法的集合，最早用于探测分子布朗运动的分布。MCMC方法是通过运行很长一段时间后形成Markov链样本，以便用样本均值近似地求数学期望。构造这种Markov链的方法较多，其中包括Gibbs抽样在内，大都是Metroplis-Hasting算法的特例，MCMC方法实质上就是利用Markov链进行Monte Carlo积分，在利用通用软件来分析许多复杂的问题时，MCMC方法可提供统一的结构框架，在多重插补中旨在通过马尔科夫链使缺失数据和参数的分布收敛，从而模拟其分布。

2.1 MCMC方法

MCMC是贝叶斯推断中一种探索后验分布的方法，下面通过正态模型说明MCMC基本思想和实施步骤，令Y=(y1,y2,…,yn)T为完全数据集，假定 y1，y2，…，yn|θ～iid Np(μ ，∑ )，其中 θ=(μ ，∑ )未知，运用该方法对该缺失数据集插补可以分为两步：

2.1.1 插补步骤

根据给定的均数向量μ和协方差矩阵∑，从条件分布 p(Xmis|Xobs,φ)中为缺失值抽取插补值。假设是两部分变量的均数向量，μ1是Xobs的均值向量，μ2是Xmis的均值向量，同时设定：

其中∑11是Xobs的协方差矩阵，∑22是Xmis的协方差矩阵，∑12是Xobs与Xmis之间的协方差矩阵。在多元正态分布的假设下，当给定Xobs=x1时，Xmis的均数为：

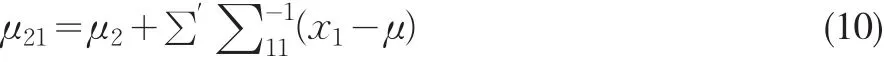
其对应的条件协方差矩阵为：

2.1.2 后验步骤

在每一次循环运算中，用上一次插补步中得到的μ和协方差矩阵对参数φ进行模拟。循环进行这两步过程，产生一个足够长的马尔科夫链：

当该链会聚在一个稳定的分布 p(Xmis,φ|Xobs)时，就可以近似独立地从该分布中为缺失值抽取插补值。

为了建立插补程序，我们必须做某些假定：首先要求对缺失机制必须做出假定，如随机缺失（MAR），如同可忽略的假定，令Yobs为观测值，Ymis为缺失值，R为回答指示变量，R的分布依赖于Yobs而不依赖于Ymis，即有P(R |Yobs，Ymis)=P(R |Yobs)；其次要求对参数的先验分布必须做出假定，多重插补必须反映插补模型参数的不确定性：

其中有：P()θ|Yobs∝L()θ|Yobsπ()θ，对于先验分布π()θ要求，推断对于π的选择不敏感。

2.2 DA算法

MCMC方法构造马氏链去模拟后验分布f(Ymis|Yobs)，可以通过DA算法实现，该方法是MCMC算法之一，特别适合于缺失数据的处理。DA算法的特点在于可以处理任意缺失模式，具体插补过程如图1所示。DA算法经过t次迭代后收敛于一个分布而不是一个值，收敛速度与数据缺失程度相关，如果数据缺失严重，收敛速度很慢，迭代的次数要多些，反之，收敛速度很快。总的来说，DA算法是重复两个步骤，即：I步，从Pr(Ymis|Yobs,θ(t))中抽取中抽取θ(t+1)。重复该过程多次，这样就建立了一条markovchain而该链收敛于P(Ymis，θ|Yobs)，这个分布就是对实际分布的预测。DA法估计的目的是从收敛的分布中随机抽取Ymis值，替代缺失数据。当有关于均值向量和协方差矩阵的先验信息时，直接利用先验信息，就可以进行迭代。当先验信息缺失时，利用大样本理论，可以认为协方差矩阵∑服从∑(t+1)|Y～W-1(n-1,(n-1)S)的分布。均值向量矩阵U服从，其中W表示Wishart分布。

使用DA去实现多重插补，为了产生恰当的多重插补，我们必须从数据增广中迭代Ymis形成或者形成m条长度为t独立链。为了估计的需要，必须有参数的初始值，通过EM进行ML估计的结果是一个很好的选择。同时应该注意的是，必须需要选择一个比较大的t以确保连续插补统计上的独立。

图1 DA算法迭代模拟过程

运用DA算法时，为使各插补值尽量保持独立，一般需迭代m×t次，得到Y(t)mis，Y(2t)mis，…，Y(mt)mis，这就是最终的m个插补值，其中t可以通过参数的时间序列图和自相关函数图(ACF)来确定，下面通过例子对这两种方法分别说明。方法一，画出参数θ与迭代次数的分布图，即θ的时序图，看其在何时趋于收敛，如果参数θ的时序图没有长期趋势，我们称之为快速收敛，如图2所示，如果存在长期趋势和变化，我们称为缓慢收敛，如图3所示；方法二，画出参数θ的自相关图(ACF)，自相关函数图估计了每次迭代参数与k次迭代参数之间的相关系数，这些图可以帮助数据分析人员去判断经过多少次迭代后参数值与初始值之间就相互独立了。每一个自相关函数图显示了一系列上下限值，在图4、图5上用两条横线表示，如果超出横线，说明自相关系数是显著的(α=0.05)。根据自相关系数收敛时的迭代次数，如果ACF很快衰减至0，我们称之为快速收敛，如图4所示，经过7次迭代后，ACF很快衰减至0；如果衰减很慢，我们称之为缓慢收敛，如图5所示，经过100次迭代后，ACF还没有衰减至0。为了得到ACF的平稳估计，特别是当缓慢收敛时，需要相当多次迭代，而且从保守的角度来看，循环次数应该足够大。一般情况下，希望自相关的初始值是正值，经过迭代很快或逐渐降为0，即使后面仍在迭代，其值仍然为0。为了提高收敛速度，在实施DA法之前，最好是先进行EM法的运算，DA算法通常以EM算法得到的结果作为初始值进行迭代。关于DA算法与EM算法之间的关系，有关研究给出了相应准则：如果EM算法经过t次迭代收敛，那么DA算法经过t次迭代几乎也确定收敛。需要注意的是EM算法收敛于一个参数估计值，而DA算法收敛于参数值的分布。

图2 快速收敛(时序图)

图3 缓慢收敛(时序图)

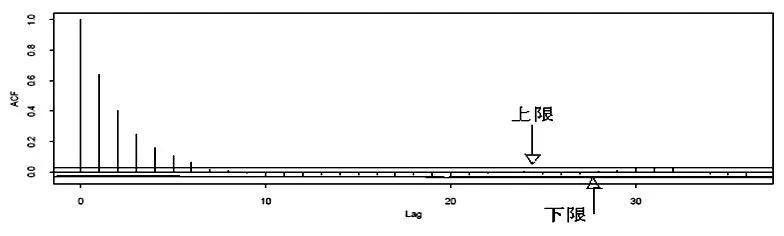
图4 快速收敛(自相关图)

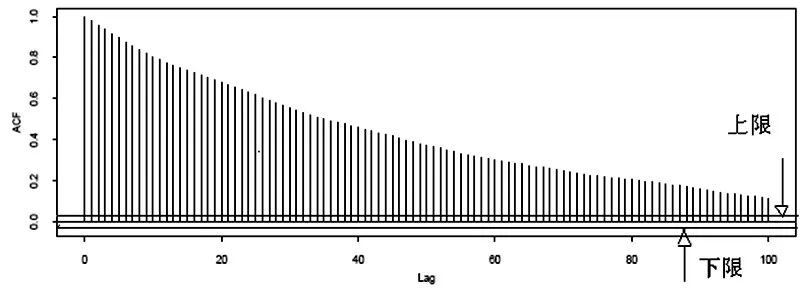
图5 缓慢收敛(自相关图)

从MCMC方法(或DA算法)的思想可以看出，基于模拟思想的多重插补也可以用于处理单位无回答，此时，只需要模拟含缺失数据变量或参数的联合分布，进行随机取值，从而创建插补数据集。各个插补数据集分析结果的合并也遵循多重插补推论和Rubin的合并规则。作为计算方法，MCMC方法(或DA算法)也存在一些不足之处：一是需要多元正态假设；二是过程复杂运算繁琐；三是对于是否收敛不好确定。庆幸的是SAS、S-PLUS、MICE中提供了MCMC运算，使得MCMC越来越成为一种主流方法。

[1][美]Roderick J.A.Little,Donald B.Rubin Statistical Analysis with Missing Data[M].New York:John Wiley&Sons INC,2002.

[2][美]James O．Berger著，贾乃光译.统计决策论及贝叶斯分析[M].北京：中国统计出版社，1997.

[3][美]Donald.B.Rubin Multiple Imputation For Nonresponse in Surveys[M].New Yrok:Jghn Wiley&Sons INC,1987.