二次调整成本模型下投资的动态分析

陈国汉，刘建平

0 引言

投资的调整成本或称为资本调整成本是指企业在投资时资本的安置成本和资本价格变动导致的成本。最直观地表现为企业购买了新的机器后，需要对机器进行安装和训练工人熟悉使用新机器由此而产生的成本。在开放经济的拉姆齐模型中，经济会瞬时收敛到稳态水平，这与现实中经济调整缓慢变动相矛盾，而当考虑投资的调整成本后我们才会得到与经验事实比较吻合的结果。大多数的理论分析都仅对调整成本函数做了比较宽泛的假定，即调整成本函数为凸函数以及投资为零时，调整成本为零。这种宽泛的假定只能得到相位图而无法得到经济从非均衡到均衡的收敛速度和相关控制变量的时间路径。因而只有在对调整成本函数做出具体假定后才可以得到均衡时的解析解。

本文拟在Pereira(2001)的二次调整成本模型的基础上使用新古典分析框架对完全竞争市场中企业的投资动态行为进行分析，使用线性二次型调整成本模型（LQAC）求解不确定性情况下的投资时间路径。

1 确定性时投资的时间路径

1.1 理论模型

假设经济中有无数个效用函数相同的家庭和技术水平相同的企业。我们从企业的价值最大化问题开始研究投资问题。生产是由许多个完全独立和竞争的厂商来执行的。为了简化起见，假设厂商的个数等于家庭的个数。每个厂商面临的利率的时间路径为{rt}t=[0,∞)，0到 t时之间的平均利率为：

令 ρ =rˉ(t) ，所以折现因子为 e-ρt。

为简化起见，不需要明确的劳动市场模型，假设劳动供给是固定的，无弹性的，劳动市场是均衡的，意味着每一个厂商雇佣一个工人，并支付工资{wt}t=[0,∞)。并假定投资行为是不可逆的，即不存在负投资。因此，有代表性的厂商在t=0时的决策问题是选择投资的时间路径以最大化其现金流量的现值，即

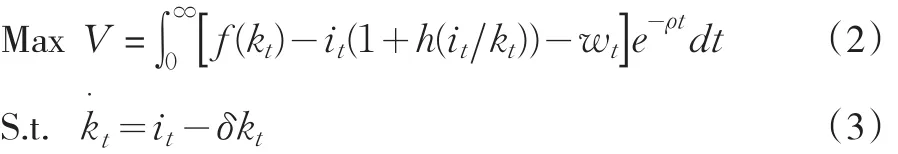
其中，所有的变量都采用人均形式。假定人口是常数，利率与时间偏好率相等。 f(kt)为生产函数，满足稻田条件 f′(⋅)＞0，f″(⋅)＜0，f′(0)= ∞ 。此模型与标准的最优增长模型唯一的不同之处是引入了调整成本或安置成本h(⋅)。为了增加i个单位的资本存量，首先得有i个单位的产出用于投资，其次需要有i h(i k)个单位的产出用于安置这些投资。因此，i单位的总投资的机会成本是i(1+h(i k))个单位的产出。调整成本函数h(⋅)是非负的凸函数，且投资为 0 时，调整成本也为 0，并有 2h′(⋅)+h″(⋅)＞0。

这个问题的汉密尔顿函数为：

解得最优性条件为：

首先考虑式（5），它表示投资从发生一直到投资的边际成本等于以安置资本的影子价格。当2h′(⋅)+h″(⋅)＞0时，影子价格q可以看做是i k的增函数。它类似于投资理论中的Tobin’s q。

对式（6）解一阶微分方程，用（7）式的结果可得：

式（8）说明影子价格q等于未来边际产出的贴现现值。

1.2 给定利率时的均衡

现在分析当利率{rt}t=[0,∞)被外生给定时的稳态和转移动态。这一假设适用于一个把整个经济范围内的利率视为给定的单个企业或者一个把世界利率视为给定的小国开放经济。为了简化起见假设世界利率r是不变的，因此ρ也是不变的。

为了获得投资的动态方程必须对调整成本函数进行设定。Gould(1968)把调整成本函数具体的设定为投资的二次函数，h(I)=a0I+a1I2。到Hayashi(1982)将调整成本函数设定为h(I,K;t)。我们遵从Goolsbee和Gross(1997)，以及Pratap(2003)的标准的二次调整成本函数的设定，调整成本为：

其中a＞0，i=0时，h()⋅=0。

如果 q·=k·=0，则 i∗=δk∗，i∗，k∗分别为稳态时的投资 和 资 本 存 量 。 且 f′(k∗)+δ2h′(δ)=(ρ+δ)[1+h(δ)+δh′(δ)]，可以证明 f′(k∗)＞ (ρ+δ)。这使得有调整成本时，其机会成本大于最优增长模型的机会成本。

系统（3）、（5）、（6）式是一个关于 (k,q,i)的动态系统，其中的q或i可以被消去。尽管q扮演了一个重要的概念角色，但本文着重分析投资的动态行为，因此消去q而得到一个关于(k,i)的动态系统。

将（5）式对时间求导，可得：

将（10）式和（5）式代入（6）式以消去 q·和 q，得：

将B代入有：

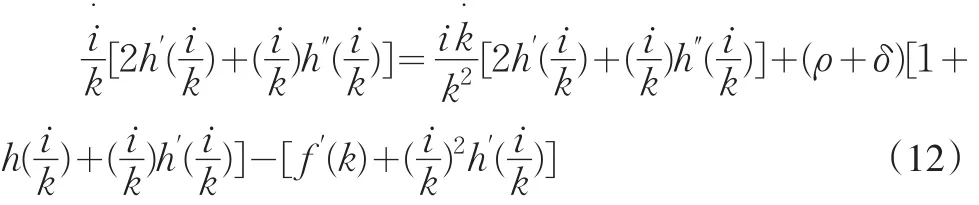
将调整成本函数（9）式和Cobb-Douglas生产函数f(k)=Akα(其中0＜ a＜1)一起代入（12）式，可以得到 i的动态方程为：

联立解得i的动态方程为：

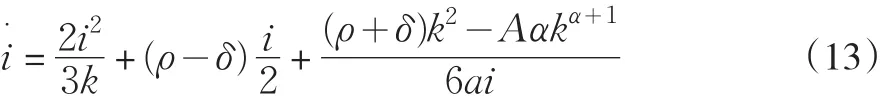
式（3）和（13）所组成的动态模型使用相位图能更容易的得出分析结果。首先确定一个(k,i)空间。在这个空间中画出 k·=0和 i·=0两条轨迹线。这两条轨迹分别由=0来描绘。

图1有调整成本模型的相位图

图1 显示了这两条轨迹线，其中k·=0为一条斜率等于δ的直线，i·=0为一条先增加后减小的曲线，两条线的交点为均衡点E(i∗,k∗)。两条轨迹线交叉产生了一条鞍点路径SS′，系统呈现出鞍点路径稳定性，以带箭头的实线表示稳定臂。这条鞍点路径是k和i的函数，它使k和i逐渐单调收敛到均衡点E(i∗,k∗)。任何不在SS′上的点都无法满足最优条件（5）、（6）、（7）。

这个模型一个有趣的特征是，只要资本折旧率为正数，那么将永远无法达到合意资本存量水平kˉ。这是因为，如果现在的资本存量正好等于合意资本存量，那么就不需要投资，调整成本为0。而如果现在的资本存量不等于合意资本存量，需要进行投资，使得资本存量到达合意的水平，即投资等于0时的水平，i=0，此时资本存量k等于合意资本存量kˉ。但是此时经济并不一定处于均衡水平，因为长期均衡要求的是i·=0，k·=0，它只发生在资本的边际机会成本等于资本的边际收益时。如果k=kˉ时经济不处于均衡水平，那么这个状态无法维持，所以只有当i·=0，k·=0且i=0时，经济的长期均衡点和合意资本存量水平重合。从图中可以看出，只有δ=0时，即k·=0轨迹线与横轴重合时，长期均衡的稳态水平资本存量k∗才等于合意资本存量 kˉ。 δ ≠ 0，则 k∗≠kˉ，合意资本存量永远无法达到。正的资本折旧率和零投资水平必然导致资本存量下降，不可能形成长期均衡。

1.3 对数线性化

传统的关于投资的动态行为的论文一般都是通过相位图来进行研究，本文在此基础上更进一步通过对数线性化的办法来得到精确的投资动态方程。通过相位图我们得到了式（3）和式（13）所组成的动态系统是鞍点均衡的。现在为了进一步的分析，对这个非线性的动态系统进行对数线性化。使用i和k的对数重新表达（3）式和（13）式，可得方程组：

在稳态中d[log(i)]dt=d[log(k)]dt=0，我们有：

围绕由（16）和（17）式所决定的稳态值水平，把（14）和（15）所组成的动态方程组取一阶二元泰勒展开：

设由（14）、（15）式所组成的方程组的Jacobian矩阵的特征值为ε，则ε为特征方程的根。特征方程为：

这个方程有两个异号的实根：

令

log(i)的对数线性化的通解有如下形式：

其中，μ1和μ2是任意积分常数。由于已知动态系统是鞍点均衡，则在 ε1＞0，ε2＜0的条件下，μ1=0；否则均衡将不稳定。常数μ2由初始条件决定：

其中，i0是投资的初始值。

将 μ1=0和（21）式代入（20）式可以得到log(it)的时间路径为：

收敛系数 β 定义为 β=-d(γi)d[log(i)]，γi=i·i。

将（22）式对t求导得到γi再与（22）式联立可以解出收敛系数β=-ε2。

式（22）可以写为：

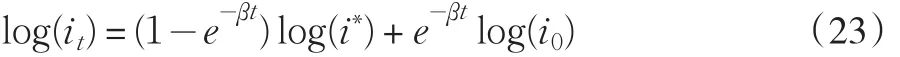
对于任何t≥0，log(it)是初始值log(i0)和稳态值log(i∗)的一个加权平均，初始值上的权重以β速率指数下降。收敛速度β依赖于折现率和折旧率。

2 不确定性时投资的时间路径

2.1 理论模型

现在假定厂商能够根据他们现有的信息集单独的决定到达稳态水平(i∗,k∗)的最可能的路径。假设厂商可以使用现在可以得到的所有信息，包括相关变量的过去值，基于理性预期去预测未来值。此时产出不再是资本的一个确定的函数，产出变成随机的。由于现存资本的重新变卖涉及到巨大的折旧，即已安置的资本重新变卖是很困难的，因此投资具有不可逆性。当市场环境恶化时，如果厂商不能削减现有资本存量，那么延迟投资或等待新信息是厂商最有利的选择，因此不确定性的本身就有阻碍投资的作用。Pindyck(1988)发现投资与不确定性有负相关性，厂商在高度变动的市场相对于较稳定的市场有更低的资本存量。Bertola和Caballero(1994)表明在不确定性和不可逆性限制下，在微观水平上总投资序列是光滑且稳定的。

现在假设总产出是给定的，那么一个风险中性的厂商的价值最大化问题就变成了一个成本最小化问题，即价值最大化等价于资本积累方程约束下的成本最小化。在这里我们使用损失函数方法，代表性厂商被假设为最小化其未来现金流量的损失。而这个损失我们把它分成两个部分：一部分是现有资本存量与资本存量目标水平之间的差异造成的不均衡损失；另一部分为投资的调整成本。Sargent(1978,1987)指出目标函数为二次函数时，能够产生线性策略函数，使得随机最优问题可以求出解析解。因此二次调整成本成为研究的热点。Sargent(1978)，Kennan（1979），Nickell（1985），Dolado et al(1991)，Gregory et al(1993)，Engsted和Haldrup（1994）等发展了线性二次型调整成本模型（LQAC），Fanelli(2000)给出了该模型的估计与检验的方法。

本文首次将损失函数设置成线性二次型调整成本模型。利用线性二次型在求解随机动态规划上的优势，可以得到精确的解析解。

考虑在离散时间下（t=1,2,…）经济法人所面对的不确定性下的序列决策问题。经济法人选择一个序列，使得跨期损失函数的期望最小化：

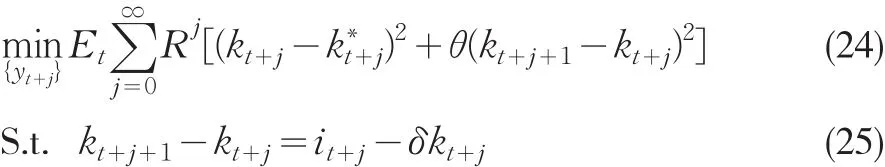
其中0＜R＜1，为折现因子；0＜δ＜1是资本折旧率。在这里k∗t不是资本存量的均衡水平，而是厂商的资本存量长期目标水平，是长期中的合意资本存量。 为不均衡损失和调整成本之间的相对权重。Et为厂商在时间t处的条件期望算子。所有的变量仍然采用人均的形式。该最优化问题的一阶必要条件为：

这个一阶条件同时也是随机欧拉方程，它决定了资本存量的最优路径。为了简化分析，假设资本折旧率为0，即δ=0。并对（26）式两端同时取t时刻的条件期望，可以得到：

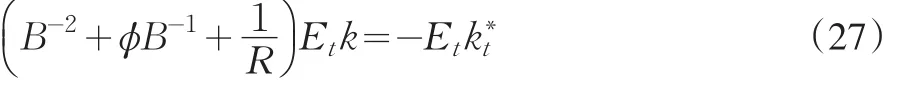
其中，ϕ=-(1+θ-1+R-1)＜0，B为由 B-jEtxt=Etxt+j定义的期望差分算子。该方程中的特征多项式有两个互不相同的实根，因此（27）式可以表示为：

其中，λ1+λ2=-ϕ ，λ1λ2=R-1。这两个等式确保方程的根 λ1和 λ2都为正。此外，由待定系数法可知(λ1-1)(λ2-1)=-1＜0，表明了这两个根中有一个大于1，另一个小于1。令 λ1＜1，λ2＞1，解（28）式可得，λ2为不平稳根，则资本存量的运动方程为：

式（29）表明当期资本存量依赖于前一期的值，同时也依赖于资本存量目标水平的当期和未来值的期望。对于投资来说，通过对（29）式的左右两端同时乘以(B-1-1)可以得到一个类似的表达式：

其中 it=Δ kt+1，i∗t=Δ k∗t+1。因此当期的投资被前一期的投资水平和合意投资水平的当期和未来值的期望共同影响。然而投资的这个合意水平i∗t是不可能被观察到的。在跨期二次型调整成本模型的研究中，资本存量的目标水平变量通常被假设为线性的依赖于一些严格外生的控制变量。因此，这里假设投资的这个合意水平i∗t与一些控制变量线性相关。

2.2 投资的动态需求方程

经典的假设是无论何时当企业的外部市场环境改善时，厂商调整到一个更高水平的资本存量。在这里我们更进一步地假设，需求影响对未来合意资本存量的预期。合意投资水平依赖于外生变量仅仅是我们定义合意水平i∗t的一个结果。如果一个外生变量影响合意的资本存量，那么它也将在同方向上影响合意的投资水平。例如：如果发生一个好的冲击，企业打算将合意资本存量在短期内调整到一个更高的水平或企业在长期中面临一个更高的资本更替需要，这些将使得合意投资增加。所以合意投资水平i∗t与外生变量线性相关的假设将极大的简化我们求出动态方程在实证研究中的应用。我们有：

其中，Xt是由可观测的控制变量组成的一个( )n×1向量，此处的β为一个( )n×1参数向量，εt是一个白噪声分布。将（31）式代入（30）式，且有 Etεt= εt，Etεt+j=0，∀j＞0，可以得到：

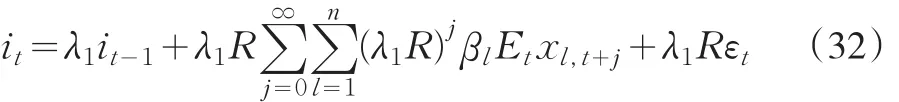
其中，βl(l=1,2,…,n)是向量 β′的行元素，xl,t是向量Xt的列元素。假设向量Xt中的每一个变量都是一个 p阶自回归过程，AR(p)：ψ(l)(L)xl,t=μl,t，其中L为差分算子。使用Wiener-Kolmogorov预测公式可得：

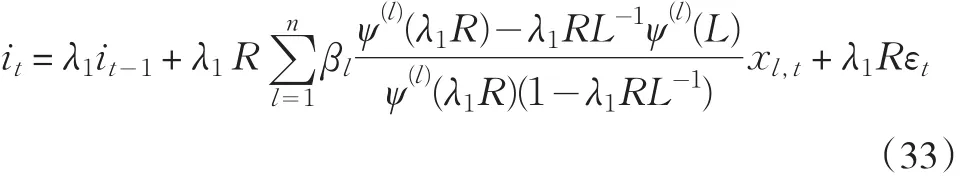
展开，（33）式可以得到：

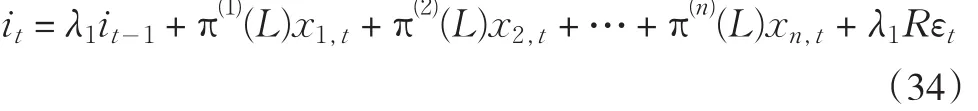
其中π(j)(L)为滞后多项式。事实上，式（34）是一个动态需求方程，它表明当期的投资需求与投资的滞后值以及控制变量的当期和滞后值相关。若调整成本函数变的更凸和θ增加时，过去资本或投资的系数增加，进而贴现率λ1R增加，这意味着厂商对远期赋予更重的权重，同时意味着需求对远期的投资水平的影响变的更大。这一模型也表达了投资与产出或需求之间的加速器关系。

3 结论

利用调整成本模型来分析投资的动态行为由来已久，但是基本上都是基于相位图来进行分析，无法得到精确的结果。本文扩展了调整成本型的投资理论，研究并证明了在新古典分析框架中使用二次调整成本模型，投资和资本存量是鞍点均衡的，并首次使用对数线性化的办法得到了精确的投资的动态方程和时间路径。发现在一般条件下，企业的资本存量均衡水平一般不等于合意资本存量水平。另外本文揭示了不确定性是如何影响资本存量的，并且首次引入了线性二次型调整成本模型分析了投资与不确定性之间的关系，得到了不确定性下投资的动态方程。

[1]Abel，A.B.，Blanchard，O.J.An Intertemporal Model of Saving and In⁃vestment[J].Econometrica，1983，51(3).

[2]Benavie，A.，Grinols，E.,Turnovsky，S.J.Adjustment Costs and Invest⁃ment in a Stochastic Endogenous Growth Model[J].Journal of Mone⁃tary Economics，1996，（38）.

[3]Duczynski，P.Adjustment Costs in a Two-capital Growth Model[J].Journal of Economic Dynamicsand Control,2002,(26).

[4]Engsted，T.，Haldrup，N.The Linear Quadratic Adjustment Cost Mod⁃el and the Demand for Labour[J].Journal of Applied Econometricas,1994，(14).

[5]Fanelli，L.A New Approach for Estimating and Testing the Linear Quadratic Adjustment Cost Model under Rational Expectations and I(1)Variables[J].Journal of Economic Dynamics and Control，2002，(26).

[6]Gould，J.P.Adjustment Costs in the Theory of Investment of the Firm[J].The Review of Economic Studies，1968，(35).

[7]Hayashi，F.Tobin’s q and Average q:a Neoclassical Interpretation[J].Econometrica，1982，(50).

[8]Kim，J.Functional Equivalence between Intertemporal and Multisec⁃toral Investmen Adjustment Costs[J].Journal of Economic Dynamics and Control，2003，(27).

[9]Lucas Jr.，R.E.，Prescott，E.C.Investment under Uncertainty[J].Econo⁃metrica，1971，(39).

[10]Mussa，M.External and Internal Adjustment Costs and the Theory of Aggregateand Firm Investment[J].Economica，1977，(44).

[11]Pereira，R.M.Investment and Uncertainty in a Quadratic Adjustment Costs Model:Evidence from Brazil[J].Revista Brasileira de Econo⁃mia，2001，(55).

[12]Pratap，S.Do Adjustment Costs Explain Investment-cash Flow Insen⁃sitivity[J].Journal of Economic Dynamicsand Control，2003，(27).