中国保费收入的预测研究

李 辉，石 龙

0 引言

计量经济学在保险领域的应用十分广泛，尤以保险行业的宏观研究为甚，国内外许多学者对此乐此不疲，建立各种计量经济学回归模型，期望从中找出影响保险业发展的因素，并以此进行定量分析和预测，从而给大众、政府和企业决策提供参考意见。然而进入21世纪，金融业数据信息交换十分频繁，人们已经不满足于年度预测模型，进而期望建立频率更快的月度模型甚至是日度和分时模型，将其运用于金融产品交易和套利、保险理财产品设计、保费现金流量管理和保费收入预测。

建立模型的前提需要有相应的数据，考虑当下我国统计数据的可得性，还难以建立全面的保费收入月度计量模型，如在2003年国家统计局GDP数据核算方法改革后就不对外公布月度GDP数据，宏观数据方面除了汇率、价格指数外及消费品零售总额之外，其他数据基本不可得，建立保险月度计量回归分析模型暂时还不可行。因此，如何建立有效的月度预测模型就摆在人们面前。本文将尝试运用保费收入的月度数据建立中国保费月度预测模型。建立模型的思路是：首先将采用当今最为热门的X12-ARIMA加法模型对保费月度数据进行季节调整，得到经调整后的时间序列和季节调整因子；其次在假设季节调整因子短期内不发生变化的条件下，采用三种“非典型计量回归分析”模型估计方法建立经调整后的时间序列模型，从而建立中国保费收入月度数据短期预测模型。

1 基本描述

1.1 季节性数据

一般地，我们需要进行季节调整，一是出于数据的可比性；二是从统计学而言，季节调整后的数值可以进行年率化的测算；三是各保险企业为制定销售计划和控制存量，从而更好地预测保险企业现金流；四是为了能够从总量中消除季节变化，从而更清晰地解释其他类型的变动，更好地反映经济周期的运动规律。

一般而言，我们可以将季节性数据分解为趋势因素、循环因素、季节因素和不规则因素。根据时间序列各组成成分之间的不同依存关系，可以建立不同的分解模型，典型的常用分解模型有加法模型(additivemodel)和乘法模型(multiplicative model)。本文将选择X12-ARIMA加法模型。

1.2 数据说明及处理

本文所用数据主要有四个：1990年1月到2011年8月名义总保费收入月度数据（Y）、财产险（PI）、人身险（包含寿险、意外险、健康险，LI）和相应的居民消费价格指数（CPI），前三者来源于保监会网站，CPI来源于BVD-EIU Country Data数据库。值得说明的是，居民消费价格指数是以2005年1月为基准的定基月度数据，处理后可得到以1999年1月为基准的月度CPI。

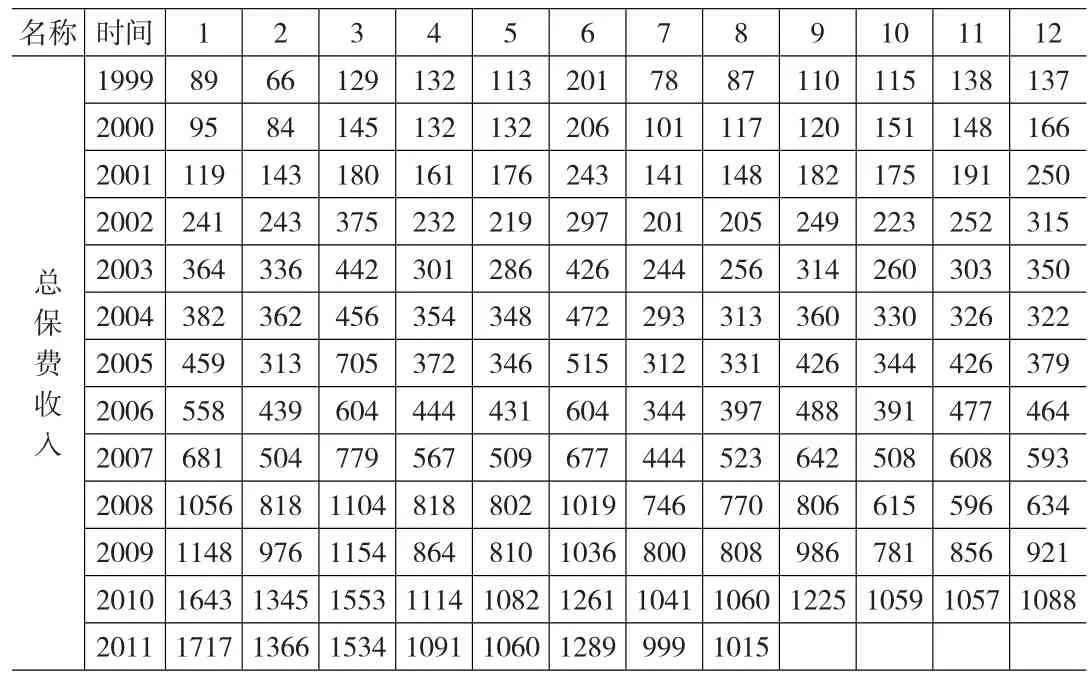
表1 我国保费收入月度数据 （单位：亿元）

数据处理步骤：第一，用得到的名义保费收入除以相应CPI数据，得到当月实际保费（YR，PIR，LIR）；第二，对实际保费数据取自然对数以平滑时间序列，得到LYR，LPIR，LLIR；第三，我们使用Census X-12加法模型进行调整，得到经季节调整后的实际保费数据（序列名_SA），趋势循环数据（序列名_TC），季节因子（序列名_SF），不规则因子（序列名_IR）。图1为平滑后实际总保费收入季节调整序列图。

1.3 统计结果

（1）Census X-12加法模型分解结果。如图1所示，LYR总体呈向上波动趋势；LYR_TC是除去季节波动后的趋势循环项，较LYR序列相比，趋势性更加明显；在加法模型下，经季节调整后的LYR_SA序列等于LYR_TC加上不规则变动序列LYR_IR；季节调整因子LYR_SF呈现出较为规律的季节波动；不规则变动序列LYR_IR头几年较为剧烈，除了2005年年初之外在接下来的若干年表现都较为平稳，平稳的不规则变动因子将对我们接下来的模型构建极为有利。

（2）季节因子（序列名_SF）。如图2所示，以1990年为基期，虽然我国保险收入呈现出较为“凌乱”的走势，规律性并不十分突出，但仔细观察，我们可以清晰地看到，每年的第一、三、六月季节因子最高，其中一月走高的可能是保险公司在完成去年保费任务后，将上年末的保单暂时留下作为来年一月的“开门红”；三月则包含中国春节因素的影响，由于二月春节保费过低而积累的需求在三月得到释放；六月则可能是半年报因素和业务竞赛的结果，各保险企业为完成半年任务，加大了优惠和促销力度以招揽客户，良好业绩源于营销力度，从而也透支了接下来七八月份的保险需求，并且结合财务因素（如半年报因素等），从而显示出超强的“六月风”，财产险和人身险均显示出类似规律，但是人身险季节性较财产险更加明显，且人身险透露出“二月低谷”现象。除了这三个月份较为特殊，其他月份则显示出较为平均的波动规律，显然，作为保险企业而言，容易利用此类信息预测各自的现金流并提高保费资金的利用率。

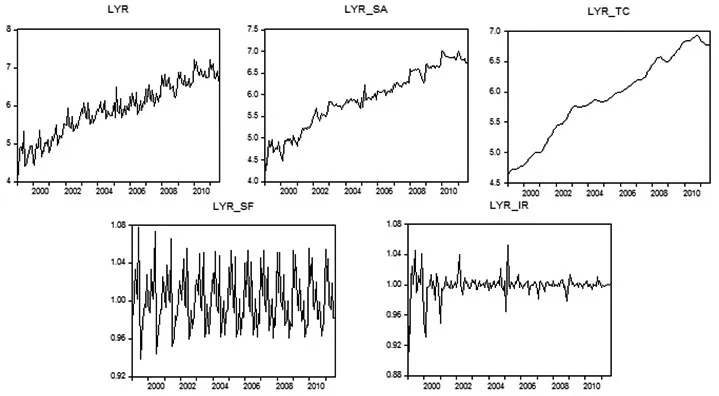
图1 经X12-ARIMA加法模型分解后各序列

（3）如表2所示，通过对总保费、财产险、人身险最终季节因子进行相关系数矩阵分析，保费总收入与人身险收入季节因子相关性更强，达到0.97，而与财产险的相关性则更低，仅为0.77。说明我国保险业总体保费收入的季节性波动受人身险季节性波动较强；此外人身险和财险之间相关性相对较弱，仅为0.63。

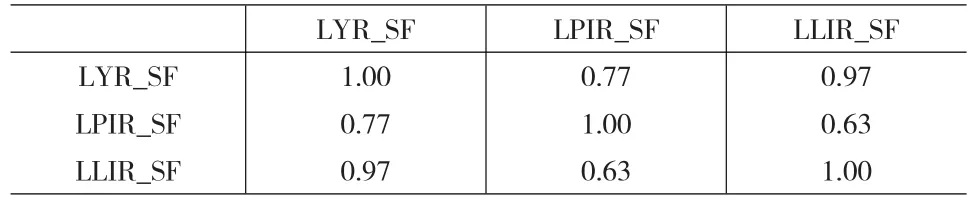
表2 保费总收入，财产险，人身险最终季节因子相关系数矩阵

（4）由于Census X-12不能对趋势循环影响分离，Hodrick-Prescott型滤波不但有消除非线性随即趋势的能力而且相位不变的特点（陈昆亭等，2004）。本文利用Hodrick-Prescott滤波法对总保费趋势循环序列LYR_TC进行分解，得到趋势项HPTREND和循环HPCYCLE，从图中可知，保费增长趋势十分明显且近似线性增长；就周期循环而言，1999～2001年为下降期，可能受1997年亚洲金融危机影响；随后逐渐递减，2003～2005年的下降可能受非典影响较大，2008年则是受国际金融海啸的影响较大；而且就保险业而言，2011年初以来的下降显示保险业目前正经历“两次探底”的过程。

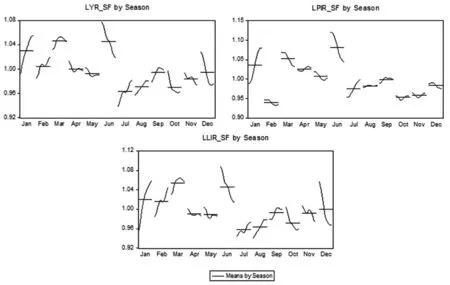
图2 每年相同月份总保费、财险、人身险最终季节因子图

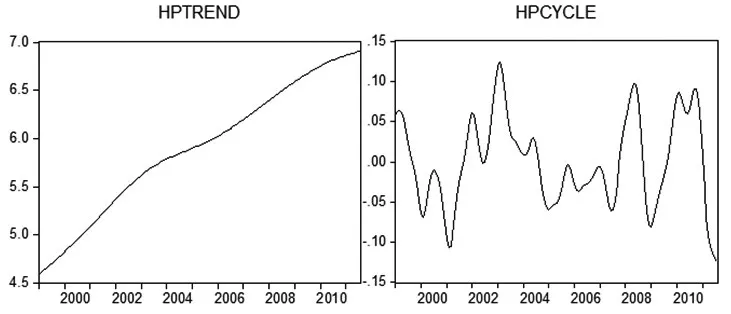
图3 经HP滤波法分解后的趋势序列和循环序列

2 建立模型

由X12-ARIMA加法模型，有LYR==LYR_TC+LYR_IR+LYR_SF（季节因子）=LYR_SA（经季节调整后序列）+LYR_SF（季节因子）。因此我们首先对中国保费收入LYR序列进行分解，得到经季节调整后序列（LYR_SA）和季节因子（LYR_SF）序列；其次，应用灰色预测、Logistic和季节ARIMA（SARIMA）三种非经典计量经济学模型，建立关于经季节调整序列LYR_SA的预测模型；再次，根据季节因子序列规律性波动的特点，尤其在后期表现更为明显，我们利用季节因子数据（LYR_SF）2010年1月到2010年8月的历史数据；最后得到的LYR2011年1月到8月的预测值，并对其进行评价。以下运用序列LYR_SA进行模型构建。

2.1 灰色预测模型

2.1.1 模型介绍

设X为经季节调整后的时机保费收入序列LYR_SA,构造各期保险保费收入的原始数据序列为：

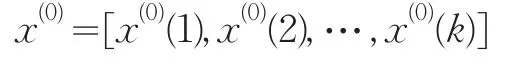
生 成数据 x(1)=[x(1)(1),x(1)(2),…,x(1)(k)]，其 中，

2.1.2 模型建立

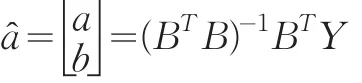
其中：

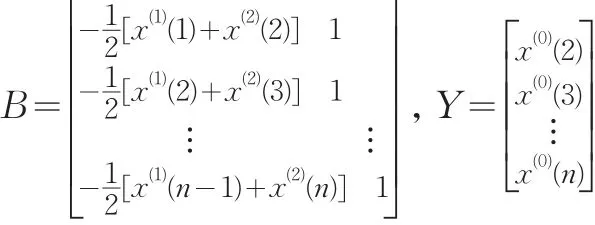
则灰色预测模型的时间响应函数为：

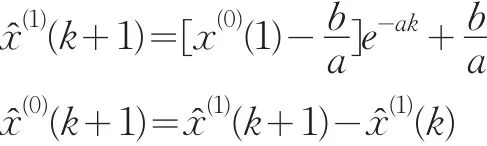
2.1.3 模型的求解

运用1999年1月～2010年12月144个经季节调整后的实际保费数据LYR_SA求解模型，剩下的2011年1月～8月的数据留待稍后验证时使用。代入数据得：

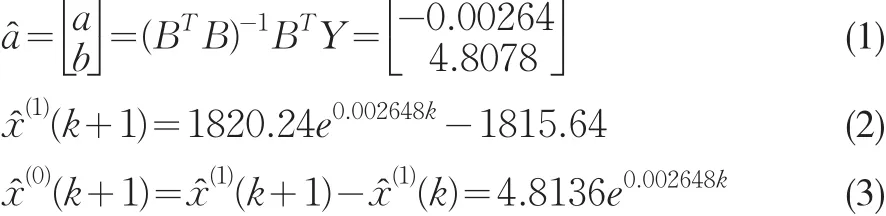
发展系数a=0.0026＜0.3，根据邓聚龙教授的分析，此时的GM(1,1)不仅适合短期预测，还可用于中长期预测。

2.2 Logistic增长模型

2.2.1 Logistic增长曲线介绍

增长曲线模型描述经济变量随时间变化的规律性，从已经发生的经济活动中寻找这种规律性，并用于未来的经济预测。但是，实践并不是经济活动变化的原因，所以增长曲线模型不属于因果关系模型。而逻辑增长曲线模型是其中的一种，俗称“S曲线”，由Verhulst于1845年提出，当时主要目的是模拟人口的增长。其一般形式为：

其中，φ(t)=α0+α1+α2t2+…+aktk。后来经过逐步简化，目前最常见的形式是：

式（5）也称为狭义的逻辑增长曲线模型。

2.2.2 逻辑曲线的估计——“三和法”

所谓“三和法”是增长曲线模型参数的一种代数估计方法。当t=1，2，…，n时，可以将样本分成3段，分别为t=1，2，…r；t=r+1，r+2，…，2r；t=2r+1，2r+2，…，n。分别计算每段中的和：

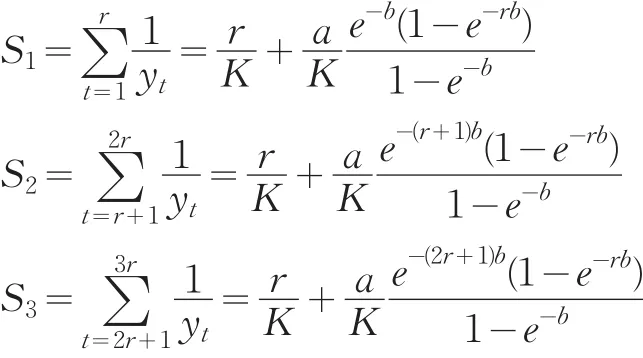
设 D1=S1-S2,   D1=S2-S3，得到：

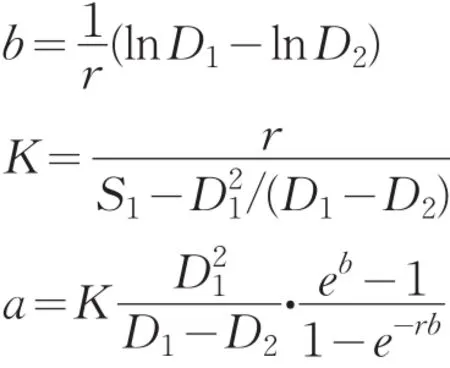
将上述得到的结果作为初值，用非线性最小二乘法进行估计。

2.2.3 模型的求解

下面将用“三和法”进行建模，与前面一样，利用1991年1月～2010年12月季节调整后的实际保费收入数据（LYR_TC），将其分为三段：

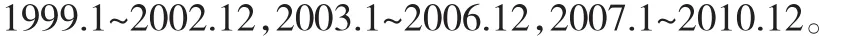
得到：S1=9.4848 ，S2=8.1439，S3=7.3066，D1=1.3408，D2=0.8374；由此算出b=0.0098，a=0.7608，K=8.1167。

将上述值作为非线性最小二乘法的初值，得到最后的非线性方程为：

所以模型估计的饱和值为K=8.2843，a=0.7837，b=0.0093。

2.3 SARIMA模型

2.3.1 SARIMA模型介绍

季节时间序列模型（seasonal ARIMA model），用SARIMA表示，较早的文献也称其为乘积季节模型。设季节性序列变化周期为s，即时间间隔为s的观测值有相似之处，首先用季节差分的方法消除周期性变化，季节差分算子定义为：

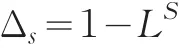
若季节性时间序列用表示，则一次季节差分表示为：

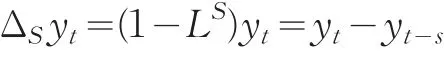
对于非平稳季节性时间序列，有时需要进行D次季节差分后才能转换为平稳的序列。在此基础上可以建立关于周期为s的P阶自回归Q阶移动平均时间序列模型（注意P、Q等于2是，滞后算子应为L2S）。

对于上述模型，相当于假定ut是平稳的、非自相关的。

当ut非平稳且存在ARMA成分时，则可以把ut描述为

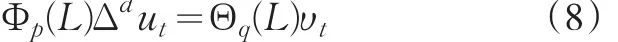
其中，为白噪声过程，p、q分别表示非季节自回归、移动平均算子的最大阶数，d表示ut的一阶（非季节）差分次数。由上式可得

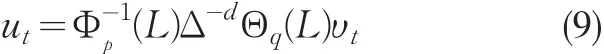
把（9）式代入（7）式，得到季节时间序列模型的一般表达式

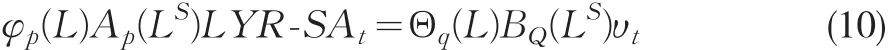
2.3.2 模型的估计

首先，对LYR_SA进行ADF检验，t统计量为-2.222，对应的概率值（P值）为0.1994，故LYR_SA序列非平稳，对其进行一阶差分，得到DLYR_SA，再次对DLYR_SA进行ADF检验。此时，t统计量为-17.40，对应的概率值（P值）为0.0000，因此对平稳序列DLYR_SA建立SARIMA模型。

其次，对差分平稳后的DLYR_SA序列建立模型，同样地，样本区间仍然为1990年1月～2010年12月，通过DLYR_SA的相关图和偏相关图决定采用何种形式的

SARIMA，经过多次尝试，对DLYR_SA进行方程估计：

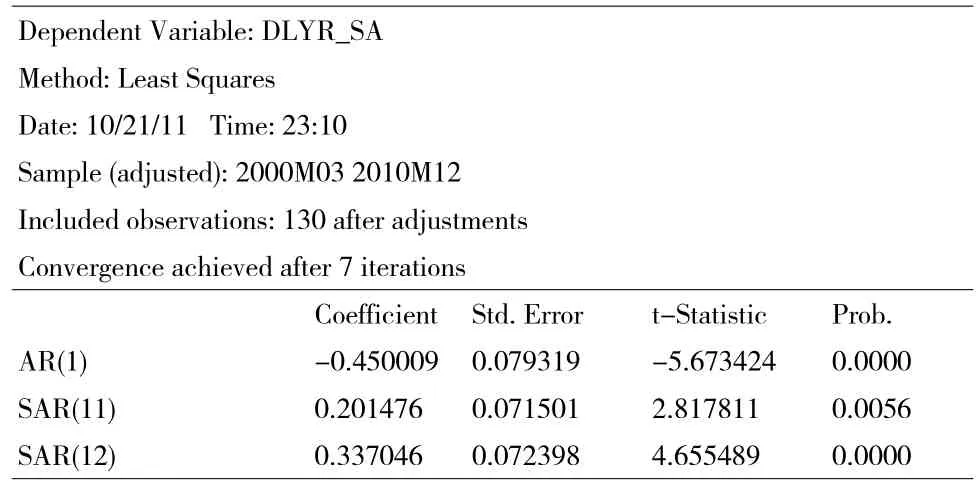
Dependent Variable:DLYR_SA Method:Least Squares Date:10/21/11 Time:23:10 Sample(adjusted):2000M03 2010M12 Included observations:130 after adjustments Convergenceachieved after 7 iterations AR(1)SAR(11)SAR(12)Coefficient-0.450009 0.201476 0.337046 Std.Error 0.079319 0.071501 0.072398 t-Statistic-5.673424 2.817811 4.655489 Prob.0.0000 0.0056 0.0000

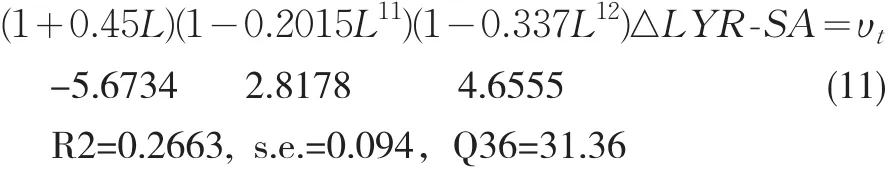
最后，用建立的方程对2011年1月到8月进行预测，得到LYR_SAF，回代预测值得到预测的。

3.4 模型对比分析

运用多建立的三种模型预测2011年至2011年8月的保费值，结果如表3。

表3 中国保费收入月度数据预测结果和误差检验

表3表明，模型的RMSE均较小，MAPE处于可接受范围。可见我们所运用的三种模型对我国保费收入月度数据进行了相对良好的拟合，也间接体现了X12-ARIMA分解时间序列数据的有效性。具体而言：

（1）从RMSE而言，三个模型的RMSE值都非常低，其中SARIMA模型最低，Logistic模型次之，说明模型良好的稳定性。

（2）从MAPE的绝对值而言，SARIMA最低，GM(1,1)次之，Logistic模型略高于10%，从MAPE的发展趋势而言，GM(1,1)先低后高，SARIMA先高后低，Logistic较为平均。因此，GM(1,1)可能更适合中国保费月度数据的短期估计；而SARIMA可能更适合较长时间段的估计；Logistic曲线模型较其它两个模型相对差一些。但考虑到Logistic模型反应更多的是长期趋势，并且又是月度数据，偏离长期趋势曲线的可能性较大，因此我们认为中国保费收入长期趋势仍是符合Logistic增长曲线。

（3）综合来看，SARIMA模型在模型中国保费月度数据时表现最为良好；GM(1,1)适合超短期预测，比如当保险企业想要预测下个月保费收入情况时；若中国保费增长的长期趋势符合Logistic增长轨迹，则可以为我们勾画出中国保险业未来长期的发展轨迹。

3 结论

在对我国保费收入月度原始数据进行X12-ARIMA季节调整之后得到的结论有：

（1）不规则变动因子LYR_SF接近预测期的若干年表现十分稳定，对我们模型的构建极为有利，也说明这几年我国保险业的发展季节性较为平稳。

（2）每年的第1、3、6月季节因子最高，其中1月走高的可能是保险公司在完成去年保费任务后，将上年末的保单暂时留下作为来年1月的“开门红”；3月则包含中国春节因素的影响，由于2月春节保费过低而积累的需求在3月得到释放；6月则可能是半年报因素和业务竞赛的结果，各保险企业为完成半年任务，加大了优惠和促销力度以招揽客户，良好业绩源于营销力度，从而也透支了接下来7、8月份的保险需求，并且结合财务因素（如半年报因素等），从而显示出超强的“6月风”，财产险和人身险均显示出类似规律，但是人身险季节性较财产险更加明显，且人身险透露出“2月低谷”现象。除了这3个月份较为特殊，其他月份则显示出较为平均的波动规律，显然，作为保险企业而言，容易利用此类信息预测各自的现金流并提高保费资金的利用率。

（3）通过对总保费、财产险、人身险最终季节因子进行相关系数矩阵分析，保费总收入与人身险收入季节因子相关性更强，而与财产险的相关性则更低，说明我国保险业总体保费收入的季节性波动受人身险季节性波动较强；此外人身险和财险之间相关性相对较弱。

（4）对趋势循环数据进行HP过滤法分解之后，保费增长趋势十分明显且近似线性增长；周期循环方面，1999～2001年为下降期，可能受1997年亚洲金融危机影响，随后逐渐递减，2003～2005年的下降受非典影响的可能性较大；2008年则是受国际金融海啸的影响，而且就保险业单个行业而言，2011年初以来的下降显示保险业目前似乎正经历“两次探底”的过程。

通过GM(1,1)、Logistic、SARIMA模型对经季节调整后的序列LYR_SA拟合之后，得到：

（1）三个模型的稳定性非常好。

（2）通过平均绝对百分比误差指标可以知道，GM(1,1)可能更适合中国保费月度数据的短期估计，而SARIMA可能更适合较长时间段的估计；再考虑Logistic模型反应更多的是长期趋势并且又是月度数据的条件下，我们认为中国保费收入长期趋势仍是符合Logistic增长曲线。

（3）根据GM(1,1)预测模型，得到的发展系数a为0.0026小于0.3，根据邓聚龙教授的分析，此时的GM(1,1)不仅适合短期预测，还可用于中长期预测。

（4）根据Logistic增长曲线模型，得到的饱和值K为8.2843，加上2011年1月到8月平均季节调整因子0.072621，则对应的保费饱和值为4259.56亿元，是2011年8月保费收入1015.30亿元的4.2倍，因此我国保险业发展潜力仍十分巨大。

（5）综合来看，SARIMA模型在模型中国保费月度数据时表现最为良好；GM(1,1)适合超短期预测，但在发展系数较小时，也可用于中长期预测；Logistic增长轨迹刻画中国保险业未来长期的发展轨迹。

[1]范维,张磊,石刚.季节调整方法综述及比较[J].统计研究，2006,(2).

[2]马永伟,施岳群.当代中国保险[M].北京：中国当代出版社,1996.

[3]栾存存.我国保险业增长分析[J].经济研究,2004,(1).

[4]孙祁祥,郑伟,肖志光.经济周期与保险周期—中国案例与国际比较[J].数量经济技术经济研究,2011,(3).

[5]陈昆亭,周炎,龚六堂.中国经济周期波动特征分析[J].滤波方法的应用，世界经济，2004,(10).

[6]席友.金融危机对我国保险业影响实证分析.保险职业学院学报[J].2010,(4).

[7]黄荣哲,农丽娜.中国保险市场宏观需求对物价波动的非对称响应——基于2000～2010年季度数据的实证研究[J].华北金融,2011,(6).

[8]邓聚龙.灰色预测与灰决策[M].武汉：华中理工大学出版社,2002.

[9]张晓峒.计量经济分析（修订版）[M].北京：经济科学出版社,2003.

[10]中国人民银行调查统计司.X-12-ARIMA季节调整—原理与方法[M].北京：中国金融出版社,2006.

[11]Damian Ward，Ralf Zurbruegg.Does Insurance Promote Economic Growth[J].Thejournal of Risk and Insurance，2000,67(4).

[12]Beck,T.,I.Webb.Economic,Demographic,and Institutional Determinants of Life Insurance Consumption across Countries[J].World Bank Economic Review,2003,17(1).

[13]Beenstock,M.,Dickinson,G.,S.Khajuria.The Relationship between Property-Liability Insurance Premiums and Income：An International Analysis of Life Insurance Demand[J].Journal of Risk and Insurance,1998,l60(4).