区域创新型经济考评综合评判模型

高卫国

如何科学评价创新型经济对区域经济发展的推动作用，又有哪些瓶颈制约着区域创新型经济的发展等，均应深入研究。目前，我国区域创新型经济考评指标体系尚未完全建立，科学评价研究还很不系统、全面。考评缺乏科学性，又缺乏判断操作上的准确性和可行性，其判断结果的置信度和说服力较低。本文拟从区域创新型经济资源类指标、过程类指标、产出类指标等三个层面的有机整合为切入点和推进路径，就区域创新型经济的综合评价体系进行深度探讨。

1 建构区域创新型经济考核评价指标体系

美国加利福尼亚大学的查德教授于1965年创立了“模糊集合论”，用它来定量描述边界模糊的事物。该科学评估及分析方法能为区域创新型经济发展评价考核提供借鉴。在此基础上区域创新型经济资源类指标、过程类指标、产出类指标三个层面的综合情况就可以用数学的方法科学准确地表示出来。

1.1 考核指标设计原则

要设计一套区域创新型经济考核指标体系和创建一个相关的数学模型，首先要明确指标体系设立的原则，考核指标体系要在此原则下设计，而数学模型要在该指标体系下设立。一般而言，区域创新型经济考核指标体系的设计应遵循以下原则：（1）发展性原则：要体现创新型经济运行的全过程，指标体系应体现创新型经济的内涵，突出创新型经济的导向作用，反映创新促进经济社会发展的作用。（2）综合性原则。创新型经济是一个综合性概念，它是以信息革命和经济全球化为背景，以人才和知识作为依托，以创新为主要推动力，以发展拥有自主知识产权新技术和新产品为着力点，以创新产业作为标志等诸多方面的综合反映。尽可能避免和克服把一时一地的具体工作作为量化考核的指标，最大限度地保证考核体系和具体考核指标的严谨性、科学性，使考核工作规范、有效地进行。(3)系统性原则。创新型经济是个系统工程。其中，科技创新是先导，产业创新是标志，开放型经济是支撑，创新型人才是基础，创新型制度是前提。所以，指标体系应能完整、系统、全面地揭示区域创新型经济的全貌，防止以偏概全，要从总目标层出发进行要素分解，逐层建立完整的评价指标体系。（4）可操作性原则。区域创新型经济评价指标要既便于进行纵向比较，也要便于进行横向比较；既要可用以进行时序比较分析，也可用来进行不同区域之间的比较分析。这就要求在选择指标时，必须考虑到指标的延续性、综合性和关联性，同时考虑支撑分析和预测的可能性；准确地分析和研究统计资料及其含义，参考统计年鉴和其他相关年鉴及文献，选用范围和口径相对一致的相对指标和平均指标。

表1 区域创新型经济运行评价指标体系表

1.2 建构区域创新型经济考核指标体系

根据相关文件规定，参考创新型经济相关资料，通过一系列的调查及比较，本文构造了区域创新型经济运行考核体系的一级指标和二级指标（见表1）。

1.3 确立指标体系中各因素的权重

确立区域创新型经济考核指标体系后，还有一项非常重要的工作就是确定权重，权重是表示各指标在评价体系中的重要程度，一般可采用层次分析法或德尔分析法来确定。假设参加区域创新型经济运行评价的人员有h位,每一位考核者把n个因素u1,u2,…,un按重要性程度由大到小排列为:ui1,ui2,…,uin.令j(j=1,2,…,n)为元素 uij的重要性序列值,即ui1的重要性序列值为1,而uin重要性序列值为n，用 f(k)j表示第k个考核者就因素ui所给定因素的重要性序列值。

当 f(k)j/f(k)i＞1时,记 p(k)ij=1;当 f(k)j/f(k)i＜1时,记 p(k)ij=0(i,j=1,2,…,n),得到h个重要性序列值评定矩阵为：

再将矩阵P各行的值累加起来,得到：

令：pmax=max{p1,p2,…,pn}，pmin=min{p1,p2,…,pn}。

令amax=1,amin=0.1，则可得级差于是可得权重ω＝(a1,a2…,an)计算公式:

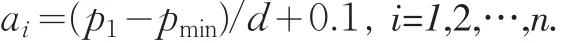
2 建立区域创新型经济运行考核综合评判模型

2.1 确定考核的因数论域

创新型经济运行考核一级指标因数模糊集可设定为：U=（U1，U2，U3）

二级指标模糊集合为：

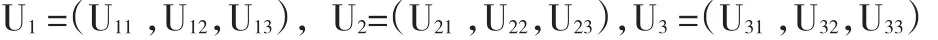
则三级指标模糊集合为：

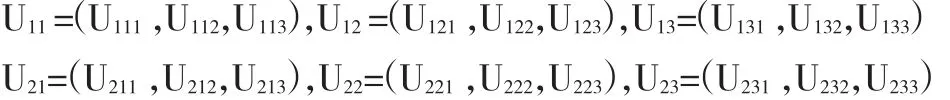
2.2 确定考核的等级论域C

确定考核等级论域使得模糊综合评价得到了一个模糊评价向量，从而体现考核的模糊特性。令创新型经济运行考核的等级论域为C，则：

C=（C1、C2、C3、C4）=（优秀、良好、合格、较差）

2.3 确定隶属矩阵

考核要素和考核等级之间的关系，即从Ux（x=1、2、3）到C的模糊关系。可用模糊评判矩阵加以描述。

R中的元素rxy（x=1，2，3；y=1，2，3）表示对应于因素Ux能被评为Cy的隶属度。

2.4 模糊矩阵运算。

先对三级指标因素层Uxyz的评价矩阵Rx作模糊矩阵运算，得到二级指标因素层Uxy对于等级论域C的隶属向量Bx；再对二级指标因素层Uxy的评价矩阵Rx作模糊矩阵运算，得到一级指标因素层Ux对于等级论域C的隶属向量B；设UX（x=1，2，3）的诸因素权重分配为Ax（x=1，2，3）,Ux的综合评判的变换矩阵为Rx（x=1，2，3），则Ux的评判结果为：Bx=Ax·Rx（x=1，2，3）[2]。

总的评价矩阵为：

又知U的权数分配为A，则得到：

则B*就是对U的所有因素的综合评判结果[3]。

2.5 综合评价结果。

综合评价结果：W=B*·CT，式中CT为C的转置矩阵，根据综合评价结果，即可确定区域创新型经济运行的优劣情况。

需说明的是，采用模糊数学中的综合评判模型对区域创新型经济运行状况进行考核与传统方法相比，它能提供更多、更全面、更细致具体的信息，它将定性与定量相结合，以量见质，给模糊现象以精确地说明。

[1]L.A.Zadeh.The Concept of Linguistic Variable and its Application to Approximate Reasoning[M].American:Elsevier Publishing Company.Inc,1975.

[2]姜启源.数学模型[M].北京:高等教育出版社，1988.

[3]青玉学.模糊数学入门[M].上海:知识出版社，1987.