交通成本、企业竞争与技术创新关系研究

陈晓暾,祝福云

0 引言

竞争与企业创新之间的关系是制定某些产业政策的重要理论依据，关于二者关系的研究文献并不在少数，包括实证研究和理论研究。本文利用消费者交通成本界定了企业竞争强度；参考张军果、任浩（2007），将企业的创新界定为通过增加研发投入来降低产品成本的方式。在此基础上构建了一个两阶段博弈模型，分析了竞争强度与企业创新动机之间的关系。研究结果表明，在纳什均衡状态下，当竞争强度相对弱时高效率企业（成本水平较低的企业）的有效研发投入水平高于低效率企业（成本水平较高的企业）的有效研发投入水平；但是，当竞争强度增强到一定程度时，低效率企业的有效研发投入水平高于高效率企业的有效研发投入水平，从而自身的成本水平将降至后者成本水平之下。本文同时分析并模拟了在不同竞争强度条件下，企业的创新决策对成本水平、产出水平、利润水平和价格水平等方面的影响，以助于增进对竞争与创新关系深层机理的了解。

1 竞争强度与研发模式的界定

1.1 关于竞争强度的定义

关于竞争强度和企业创新方式的界定是本文研究的关键。近年来，在中国的城市或地区之间以及城市内部都进行了大量的交通基础设施建设，无论是高铁、城际铁路，还是城市地铁，都极大程度地方便了人们的工作与生活。消费者的购物成本降低了，企业经营环节的交通成本降低了，物流、信息流等变得更加通畅。从消费者的购买决策看，商品价格和交通成本是影响消费者购买决策的重要变量：当交通成本非常高的时候，消费者更愿意选择近处的企业购买商品，企业对当地的消费者的垄断性较强；当交通成本降低的时候，价格差异在消费者购买决策中的影响力会变大，价格调整在企业争夺市场份额中的作用变得更加重要，企业间的竞争强度增加。可见，消费者交通成本间接地成为了企业间通过价格竞争来争夺消费者的决定因素。因此，本文以消费者单位距离的交通成本t为基础定义了企业间的竞争强度。如式（1），本文将θ定义为竞争强度。当t比较高时，θ值较小，即竞争强度较弱；当t比较低时，θ值较大，即竞争强度较强。

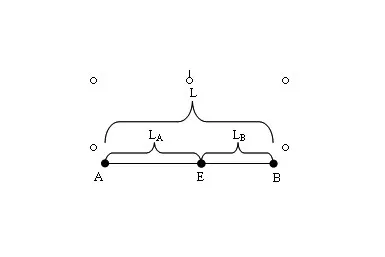
图1 市场竞争态势

1.2 关于研发模式的界定

价格的调整需要企业有效的成本控制，通过研发活动进行创新是从根本上降低成本的手段。本文分析中，创新对于企业的直接作用是降低产品生产成本。假定企业采用的研发形式是自主研发，而不是购买专利或者合作研发等形式。假设1和假设2分别是关于创新使企业成本降低的程度和企业围绕研发活动投入的成本的定义。假设1设企业研发投资后形成的新的成本水平为：其中，Xi是企业i的有效研发投资水平，f( )Xi是企业i的有效研发投入使其成本降低的程度，假定有效研发投入水平越高，企业成本降低程度越大，反之越小，即f'( )Xi＞0。

假设2在不存在技术突变的情况下，基于研发投入的边际效用递减规律，设企业围绕研发活动所形成的全部投入成本为：

系数n衡量了研发投资的效率，n＞0。

2 博弈模型的建立与分析

假设市场上存在两个效率不同的企业，分别为企业A和企业B。二者的单位产品成本水平分别为CA和CB，且CA＜CB，即企业A为高效率企业，企业B为低效率企业。两企业分别位于直线距离为L的区域两端，如图1所示。消费者均匀分布于该直线区域上，分布密度为1，即每隔单位距离有一个消费者。消费者购买商品所花费的总的交通成本与距离目标企业的距离成正比。如图1所示，其中E点为均衡点，在两个企业价格水平没有变动的情况下，出于交通成本的原因，位于E点左侧的消费者会选择企业A，位于E点右侧的消费者会选择企业B。假定每个企业的销售量不为零，根据图1，企业A和企业B的争夺到的地盘分别为 ||AE=LA和 ||BE=LB。根据消费者均衡分布假设可知，企业A和企业B各自争夺到LA和LB个顾客。设两企业产量分别为QA和QB，且假定产销恰好相等，则QA=LA，QB=LB。

根据以上描述，在竞争均衡点E，有如下关系：

其中p表示商品价格。已知QA+QB=L，可以解得两企业的需求函数为：

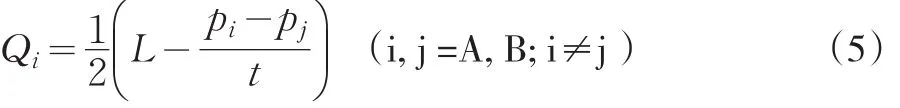
其中i代表企业A或企业B，Pi为企业i的价格水平，C'i为企业i新的成本水平，Yi是与企业i围绕研发活动形成的所有投入。

根据式（2）、（3）、（5），新的利润函数为：

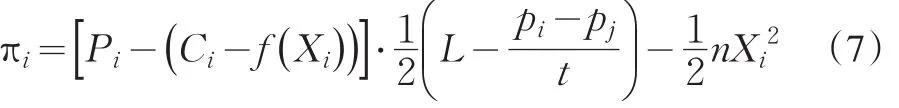
2.1 企业的竞争与研发博弈

假设两个企业的全部博弈过程为一个两阶段完全信息静态博弈，其结果是子博弈完美纳什均衡。第一阶段为研发阶段，在研发竞争背景下，两个企业选择各自的研发投资水平以降低成本水平；第二阶段为企业价格决策阶段。模型中企业竞争的直接目的表现为通过商品价格水平影响消费者决策，进而实现自身利润最大化。本文采用逆推法求解此两阶段的子博弈完美纳什均衡。

2.1.1 企业的价格决策

在博弈第二阶段的价格决策阶段，两企业在各自利润最大化条件下独立决定各自价格水平。企业的利润函数为：

根据利润最大化一阶条件∂πi/∂Pi=0，可得企业i的价格反映函数为：

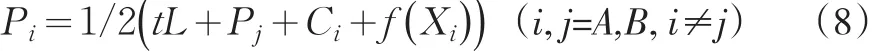
因此可得纳什均衡条件下企业i的价格水平：

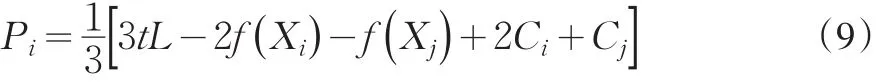
根据式（5）和式（9）可得纳什均衡条件下企业的销售量为：

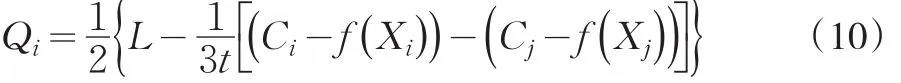
设企业i的市场占有率为Si，市场处于纳什均衡状态时：

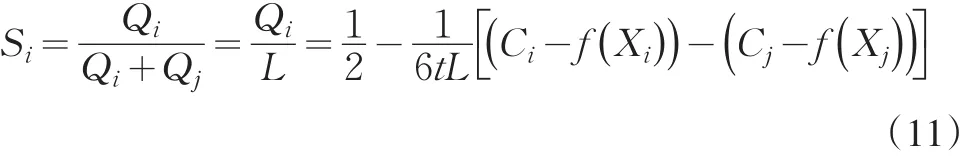
至此，可得纳什均衡状态下的利润函数：

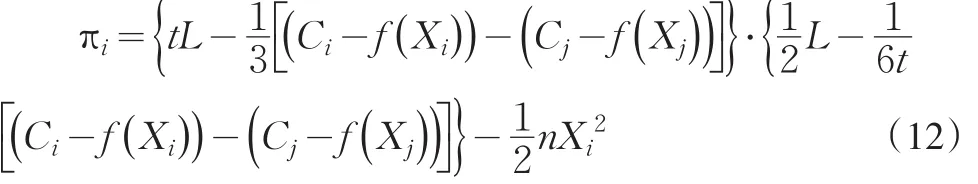
由于两企业间的距离L、各自的初始成本水平外生给定，因此，式（9）、式（10）、式（11）说明企业i的价格水平Pi、产出水平Qi和市场份额Si最终与消费者交通成本t、企业i自身的研发投资Xi、企业j的研发投资Xj有关。

从式（9）可推知∂Pi/∂t＞0，∂Pi/∂Xi＜0，∂Pi/∂Xj＜0。由此可以推出命题1：

命题1企业i的价格水平与消费者交通成本t正相关，与竞争强度θ负相关；与自身的研发投入以及企业j的研发投入负相关。

从式（10）和式（11）可推知 ∂Qi/∂Xi＞0 ，∂Qi/∂Xj＜0 ，∂Si/∂Xi＞0，∂Si/∂Xj＜0。由此可以推出命题2：

命题2企业i的产量水平Qi和市场份额Si与自身的研发投入Xi呈正比，与竞争企业的研发投入Xj呈反比。

从式（10）和式（11）同时可以得到

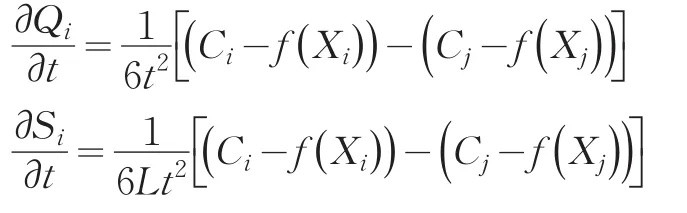
企业i的产量水平Qi、市场份额Si与交通成本水平t的相关性是由创新后两个企业新的成本水平之差决定的。由此可以推出命题3：

命题3当企业i自身的新成本水平高于竞争对象的新成本水平的时候（即当C'i＞C'j时），它的产量Qi和市场份额Si与交通成本t正相关，与竞争强度θ呈负相关；反之则与交通成本t负相关，与竞争强度θ正相关。

式（12）对Xi分别求一阶导数和二阶导数，得：

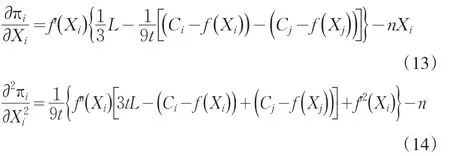
当∂2πi/∂X2i＜0时，企业利润函数存在最大值。

式（12）对Xi和Xj求二阶混合偏导数，得：

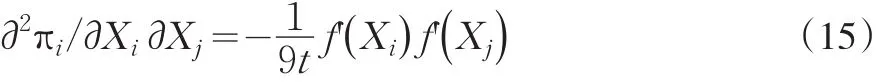
可以推知式（15）小于零，因此可以得到命题4：

命题4 企业i自身的研发投入水平Xi与竞争对手企业j的研发投入水平Xj对企业i的利润水平πi的影响方向是相反的。

式（12）对企业i自身的研发投入Xi和单位距离交通成本t求二阶混合偏导数，得：

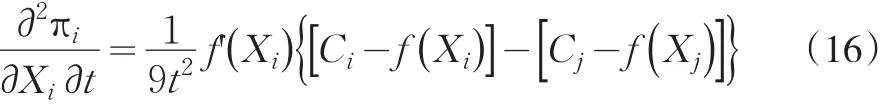
式（16）的符号受企业i和企业j新的成本水平之差影响。因此可得到命题5：

命题5当企业i新的成本水平高于竞争对手企业j的新成本水平时（即当C'i＞C'j时），企业i的研发投入水平Xi与交通成本t对企业i利润πi的影响方向是相同的，此时Xi与竞争强度θ对πi的影响就是相反的；反之，当C'i＜C'j时，Xi与t对 πi的影响方向是相反的，此时 Xi与竞争强度θ对πi的影响是相同的。

2.1.2 研发阶段分析

为简化运算但不失普遍性，假设研发使企业成本降低的程度为：

则企业新的成本水平为：

根据式（12）和式（17），企业的利润函数形式变为：

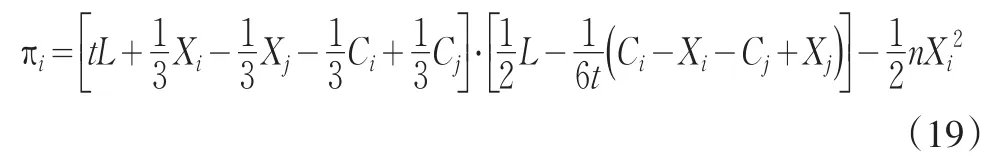
根据最大化一阶条件∂πi/∂Xi=0，可得：

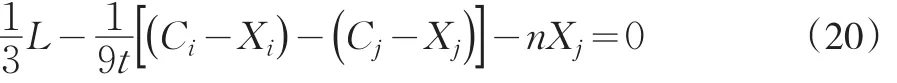
根据符号对称性可得企业各自最优研发投入水平为：

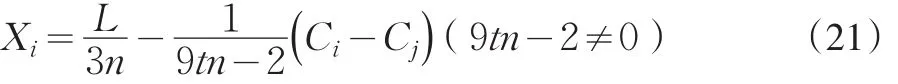
2.2 基本结论

从式（21）可以看出，企业i的研发投入水平Xi与两企业间的距离L、研发活动成本参数n、竞争强度θ（交通成本t）、企业间的初始成本之差有关系。假定除t外的其它变量外生，研发投入与t之间呈现双曲线的关系。根据t与本文定义的竞争强度θ的关系可以看到，竞争强度θ与企业研发投入之间存在如下的关系：

假设初始情况下企业i的效率高于企业j的效率，即假定 Ci＜Cj，则有（1）∂Xi/∂t ＜0，∂Xj/∂t ＞0 ；∂Xi/∂θ ＞0，∂Xj/∂θ ＜0 ；（2）当9tn-2＞0时，Xi＞Xj；当 9tn-2＜0 时，Xi＜Xj。

可以看到，高效率企业的研发投入与竞争强度呈正比，低效率企业的研发投入与竞争强度呈反比。即随着竞争强度的增加（交通成本t的降低），高效率企业的研发投入会逐渐增加，而低效率企业的研发投入会逐渐降低。从研发投入的大小来看，两企业的研发投入的相对大小与9tn-2是否大于零有关。当9tn-2＞0时，企业i的研发投入大于企业j的研发投入；在9tn-2小于零的区域，企业j的研发投入高于企业i的研发投入。图1是对不同竞争强度情况下（t值不同的情况下）企业i和企业j的研发投入的变动情况的模拟。其中，设Ci=3，Cj=3.1，n=0.5，L=3。

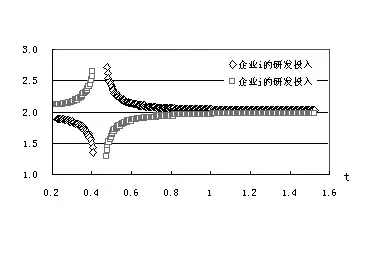
图2 企业研发投入随t变化的情况

从市场整体看，研发投入的大小与企业相对效率的大小不呈单调关系。在右边竞争强度相对弱的区域（交通成本较高），高效率企业的研发投入高于低效率企业的研发投入；在左边竞争强度相对强的区域（交通成本较低），低效率的企业研发投入高于高效率企业的研发投入。

3 竞争强度对企业绩效和顾客购买成本的影响

上文分析了竞争强度对企业研发投入的影响。那么，在竞争强度与企业研发投入关系的背后，每个企业的成本水平、产量、商品价格以及企业利润都在相应地发生怎样的变化？两个企业的相对绩效变化情况如何？竞争强度变动对消费者利益又会产生什么样的影响？

依据上文分析可得纳什均衡条件下两企业的研发投入水平、研发投入水平之差、成本水平、成本水平之差、产量、产量之差、市场份额、市场份额之差、利润之差的表达式，如表1所示。表1同时显示了上述各项目对交通成本t的导数。各导数的符号与9tn-2的值有关，如表2所示。表2同时显示了上述各项目对竞争强度θ的导数，其值的符号与各项目对t的导数相反。

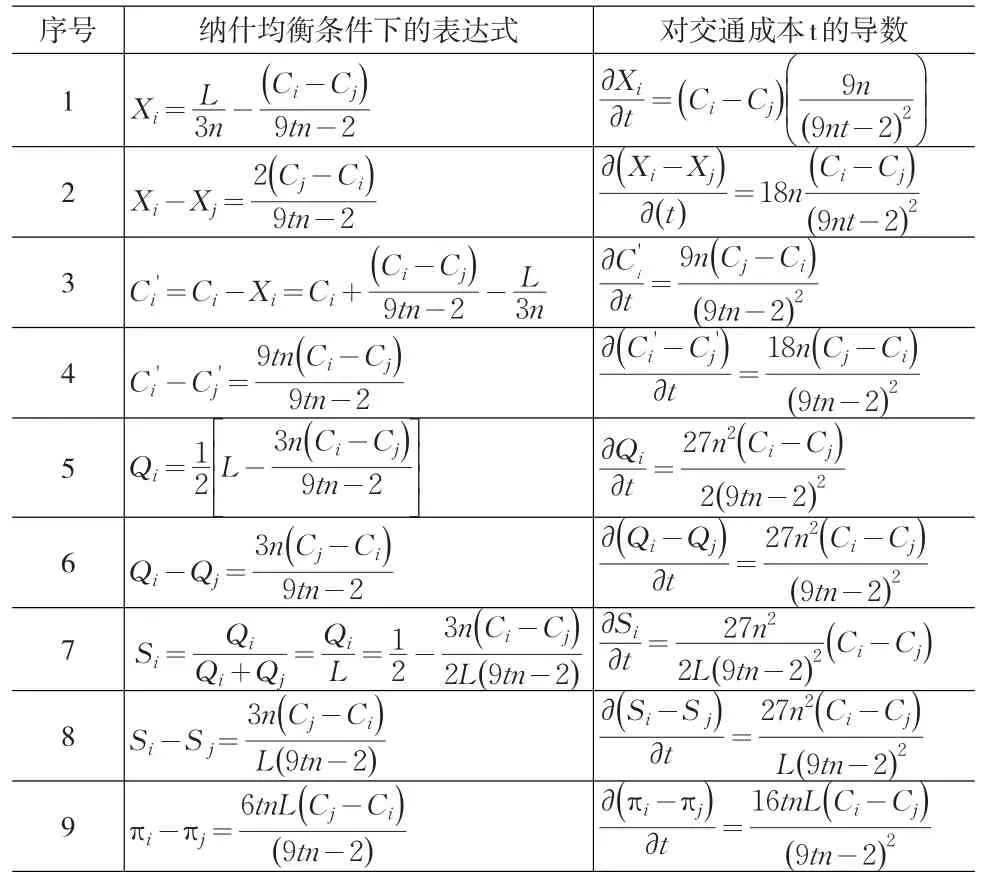
表1 纳什均衡条件下企业的研发投入等指标与交通成本t的关系

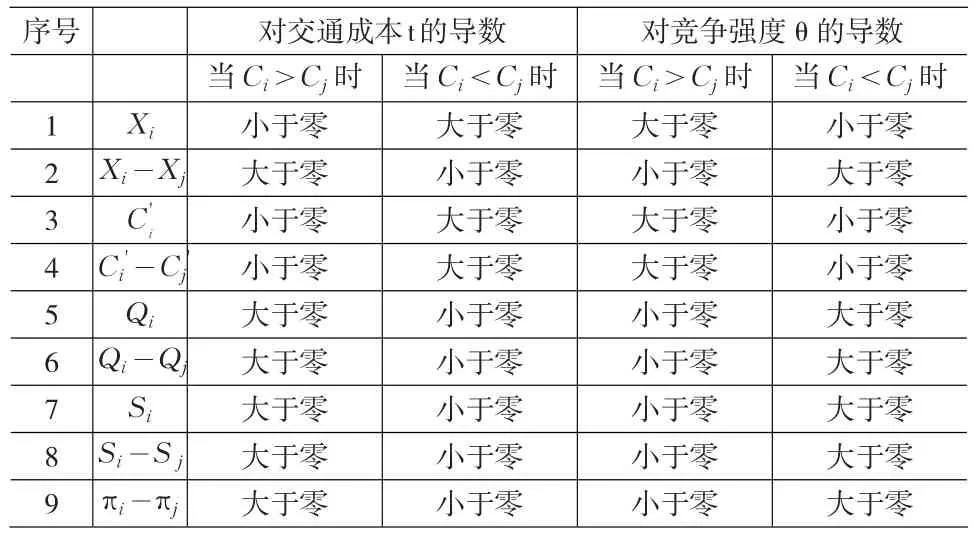
表2 各项目对交通成本t和竞争强度θ的导数取值情况

从表1和表2可以看出，当9tn-2＞0时，Ci'与竞争强度成反比，Cj'与竞争强度成正比；Ci'小于Cj'，两者的差距随竞争强度的增加逐渐加大。企业i和企业j的产量、市场份额、利润的相对大小情况与二者成本相对大小的情况相反。即当9tn-2＞0时，Qi＞Qj，Si＞Sj，πi＞πj，企业i和企业j在这三个变量上的差距随竞争强度的增加而增大。当9tn-2＜0时，Ci'与竞争强度成正比，Cj'与竞争强度成反比；Ci'大于Cj'，两者的差距随竞争强度的增加逐渐减少。此时，Qi＜Qj，Si＜Sj，πi＜πj，企业i和企业j在这三个方面的差距随竞争强度的增加而减少。

从表1、表2可以看出，当竞争强度取极限值时，无论趋于正无穷大还是趋于零，企业i和企业j的研发投入、成本、产量、市场份额、利润、价格水平都趋于相同。不过，两处极限值相同的原理却不相同。当竞争强度极大时，是由于竞争的结果；当竞争强度极小时，是由于企业当地垄断的结果。

企业利润水平和价格水平的总体变动趋势更能明显地反映竞争强度由弱至强对企业的影响。总体上看，随着竞争强度的增加，两个企业的利润水平、价格水平总体呈下降趋势；当竞争强度极大时，两个企业的利润均趋于0，而此时两个企业的价格水平也趋于相同，这时的市场状态接近于完全竞争市场。

对于消费者而言，商品价格和交通成本的降低均有利于提升消费者福利。如果把商品价格看作消费者获得的价值量的话，那么消费者每单位交通成本平均能获得的价值量可以从一个侧面衡量消费者福利的变动。从图13可以看出，随着竞争强度的增强，消费者每单位交通成本平均能获得的价值量虽然未呈单调变换的趋势，但是总体呈上升趋势。

4 结论

本文借助消费者购物交通成本界定了企业间的竞争强度，交通成本的改变会引发消费者在不同企业间的购买决策。企业无法改变消费者购物的交通成本，但是可以通过调整商品价格来影响消费者决策，而通过创新降低成本是企业调整价格的基础。本文的分析路径可以概括为：交通成本变动→消费者决策的改变→企业价格决策的调整→企业研发投入的调整。

关于竞争强度与企业创新的关系，从单个企业的研发投入看，其与竞争强度呈单调关系。但如果以随着竞争强度的变化哪一个企业的创新动机更强烈来衡量竞争强度与创新的关系，那么两者之间呈现的是非单调关系。表现为：交通成本较高的区域，企业间的竞争强度相对较弱，原来高效率企业的创新动机更强；但是，在交通成本较低的区域，企业间的竞争相对激烈，原来低效率的研发投入会更高。

一般认为，市场集中度较高的市场缺乏竞争，而竞争比较激烈的市场的市场集中度相对低。但是，从本文的研究看，竞争强度与市场集中度之间也非单调关系。恰恰存在着随着竞争强度的增加，市场集中度也逐渐增加的现象。因此，当实施了某些刺激市场竞争的措施后，市场的集中度却变得更强的现象是可能存在的。

根据本文的分析，当消费者单位交通成本水平t接近零，即竞争程度极大时，企业市场份额、利润水平等变量都变得非常接近，市场结构趋于完全竞争的市场。在t从极大值向接近零值变动的过程中，消费者的福利总体上呈上升的趋势。

[1]Aghion,P.,Bloom,N.,Blundell,R.,Griffith,R.,Howitt,P.Competi⁃tion and Innovation:an Inverted-U Relationship[J].Quarterly Journal of Economics,2005,(120).

[2]Chang Y.L.Competition Favors the Prepared Firm:Firms’R&D Re⁃sponsesto Competitive Market Pressure[J].Research Policy，2009,(38).

[3]Tang,J.Competition and Innovation Behavior[J].Research Policy,2006,(35).

[4]Boone,J.Intensity of Competition and the Incentive to Innovate[J].In⁃ternational Journal of Industrial Organization,2001,(19).

[5]陈志广.熊彼特的竞争理论及其启示[J].中南财经政法大学学报,2008,(1)

[6]张军果，任浩.吸收能力与竞争企业研发投资及方式选择[J].系统工程,2007,(4).