42CrMo钢传动轴再制造后寿命预测技术研究
2012-09-26柳忠雨张继林马鹏鹏
柳忠雨 张继林 马鹏鹏
(①徐工集团工程机械股份有限公司建设机械分公司,江苏徐州 221000;②塔里木大学机械电气化工程学院,新疆阿拉尔 843300;③徐工集团工程机械股份有限公司科技分公司,江苏徐州 221000)
重型机械传动轴往往受多轴循环应力-应变载荷下作用,其主要破坏形式为多轴疲劳断裂。目前单轴疲劳研究已较为成熟,在多轴预测方面国内外学者已经做了大量工作,Miller和Brown认为最大剪应力是裂纹萌生的主要力量,最大剪平面上的主应变是修正因素的观点推导出疲劳寿命计算公式[1]。尚德广等利用多轴临界面上的剪切应变幅与相邻两个最大剪切应变值之间的法向应变幅作为形成多轴疲劳损伤参量的主要参数,提出拉伸和剪切两种形式的多轴疲劳损伤模型[2]。近些年,零、部件的再制造所产生巨大的社会、资源、经济、环保效益逐渐深入人心。而再制造传动轴能否满足下一个寿命周期的需要是其再制造本身价值体现的根本依据[3]。其中,张国庆根据再制造修复工艺通过试验的方法得到修正系数预测曲轴寿命[4]。当前我国对再制造产品寿命预测研究刚刚起步,尚有广阔的研究空间。
针对传动轴再制造后全寿命的定量预测,由于其再制造后材料的初始条件发生很大变化,这对评定寿命提出新的要求。本文基于多轴疲劳临界平面法的寿命预测方法,并结合再制造后疲劳寿命修正系数,对再制造零件——传动轴(材料42CrMo钢及其带3Cr13电弧喷涂涂层)的全寿命进行定量研究。
1 疲劳损伤模型
在实际工作状态中,传动轴主要承受一定的弯曲和高的扭转荷载,因此该传动轴其失效模式主要是恒幅多轴疲劳失效。多轴疲劳寿命分析包括等效应力应变法,能量法和临界平面法3种方法。临界平面法是目前公认的解决多轴疲劳问题最有效、最有前途的方法。国内外学者基于不同的临界面损伤参量,提出了不同的多轴疲劳寿命预测模型。在比例加载条件下,Brown-Miller模型预测多轴疲劳寿命与实际模拟结果比较接近,预测结果比较理想。该模型认为最大剪应力是裂纹萌生的主要力量,最大剪平面上的主应变是修正因素。这种观点最先被Miller和Brown提出来,经过进一步的完善,该疲劳寿命预测模型表示为:式中:Δγmax为最大剪应变幅值;εn为最大剪应变平面上的正应变幅值;k为多轴参数;σ′f为疲劳强度系数;b为疲劳强度指数;c为疲劳塑性指数;E为弹性模量。
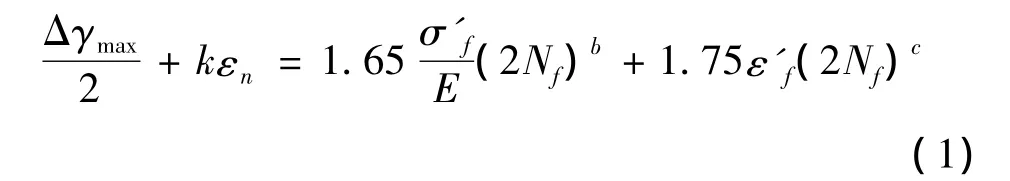
经修正系数改造获得再制造后疲劳寿命预测模型为
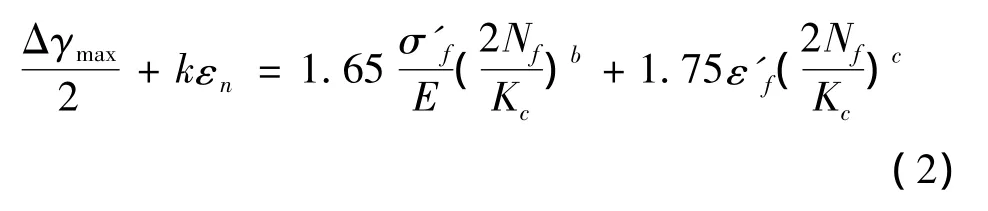
式中:Nf为再制造后全寿命;Kc为修正系数。
2 临界平面——修正系数
2.1 损伤临界平面确定
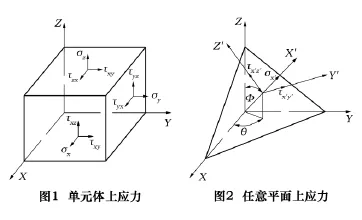
如图1所示,一般应力状态下的一个微元体都包含六个独立的应力分量 σx、σy、σz、τxy、τyz、τxz在一定的外力条件下,受力物体内任意点的应力状态是确定的,如果取不同的坐标系,那么表示该点应力状态的6个独立应力分量将会有不同的数值。如图2所示,新的空间直角坐标系中X′与新平面垂直,Y′、Z′两个坐标轴所形成的平面与新平面平行。θ为X′在X-Y平面上的投影与X夹角,φ为X′与Z的夹角。这样只需要两个欧拉角θ、φ就可以确定新坐标系与原坐标系之间的转换关系。新坐标系中各应力表示为
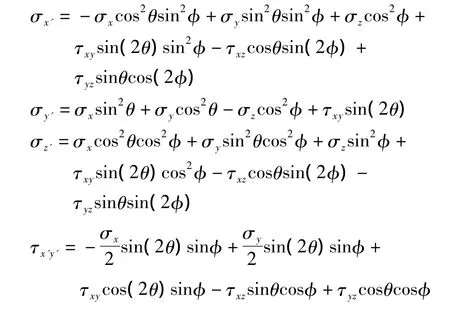
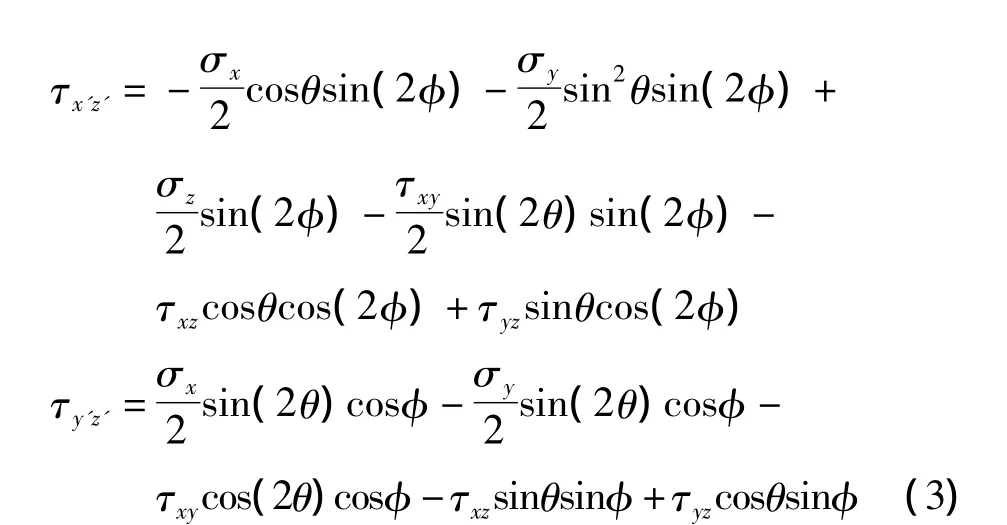
也可求得任意平面上的6个独立应变分量,只需把上面各式对应的应力换成应变分量,即σx、σy、σz、τxy、τyz、τxz用 εx、εy、εz、γxy、γyz、γxz替换即可。依此方法所得最危险平面即为临界平面。
2.2 再制造后寿命修正系数确定
制备指定涂层厚度的试件在疲劳试验机上进行试验。根据疲劳实验结果,运用升降法较准确地计算出指定涂层厚度的再制造传动轴疲劳极限。舍弃第一对相反结果前的数据,将所有邻近出现相反结果的数据配成对,由这些成对应力求得的平均值可做为疲劳极限精确值[5]。

式中:vi表示在第i级应力σi下进行的试验次数;n表示试验总次数;m表示应力水平的级数。
那么
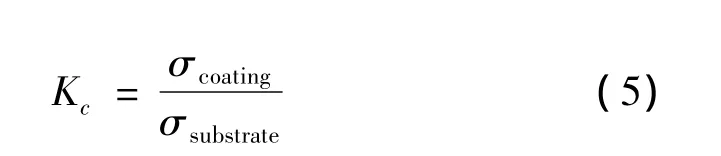
式中:σcoating带涂层试件疲劳极限;σsubstrate基体材料试件疲劳极限。
3 算例验证
3.1 建立有限元模型
传动轴材料为合金钢42CrMo,该材料的性能参数为:弹性模量E=210 GPa,泊松比μ=0.3。利用ANSYS对传动轴的弹塑性有限元分析,选择经典双线性随动强化模型(BKIN)且使用VonMises屈服准则来定义材料的非线性属性。单元类型为Solid95,并采用自由网格划分,结果如图3所示。
根据输入轴受载实际情况,输入轴径向支承为面支承,故对在轴与轴承油膜接触面上施加约束。由于轴承和轴采用过盈配合,故对轴承内圈和轴使用绑定约束,而轴承外圈由轴承支座支承,故对轴承外圈固定。分析结果如图4所示,最大应变点的应变分量见表1。

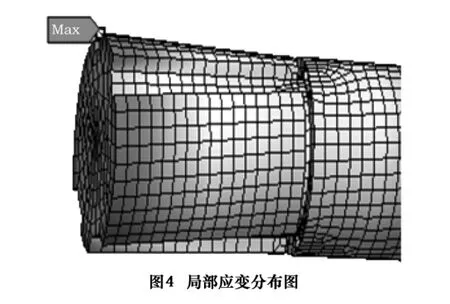

表1 最大应变点的应变分量
3.2 临界面的确定
欧拉角 θ在(0°,180°),φ 在(0°,90°)内按步长为5°来寻找临界平面。将表1结果代入式(3)得:最大应变点的最大剪应变幅出现在10253节点θ=180°、φ=25°的平面上,其最大剪应变Δmax/2=0.006 7,最大剪应变上的正应变εn=0.001 8。
3.3 各涂层厚度的修正系数
分别测试4组试样,每组3个试样,其中一组试样材料是42CrMo,另3组是基体为42CrMo,并分别带有0.1 mm、0.2 mm和0.3 mm的3Crl3涂层试样。试验结果如图5。
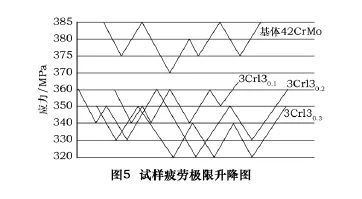
结合式(4)得:σ-1=378.2 MPa,σ-1(0.1)=349.3 MPa,σ-1(0.2)=340.7 MPa,σ-1(0.3)=332.1 MPa。再由式(5)得:Kc0.1=92.36% 、Kc0.2=90.08% 、Kc0.3=87.81%。
3.4 寿命预测结果
将修正系数 Kc0.1、Kc0.2、Kc0.3和 42CrMo 钢多轴疲劳参数[6-7]见表 2,代入式(2),得表3 寿命结果。

表2 多轴疲劳参数
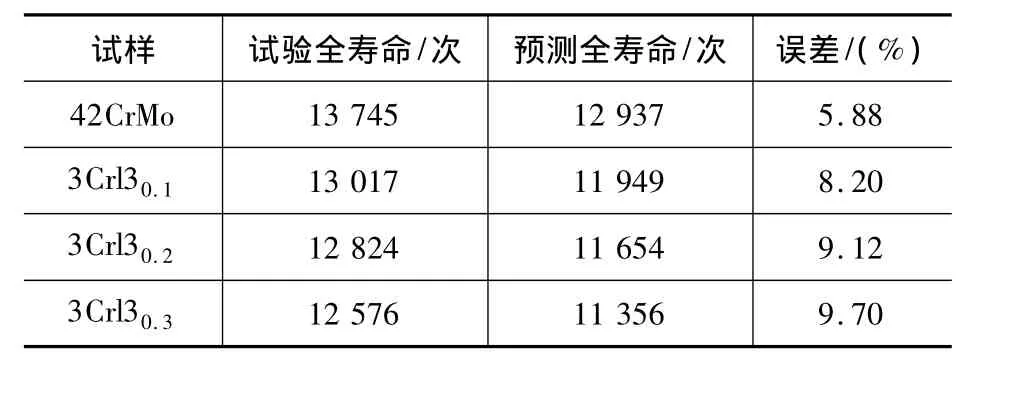
表3 寿命预测结果及分析
表3数据显示表明,预测结果也基本能反映试验情况。同时再制造传动轴涂层厚度越厚其实际和预测寿命减少量越多。这是由于涂层厚度影响着疲劳性能,主要原因是涂层的结合强度较低,以及喷砂时残留的铝氧化物引起的。
4 结语
(1)为了定量分析再制造传动轴的疲劳寿命,本文提出并建立了一种基于涂层材料修正系数的多轴疲劳损伤模型,采用该方法进行的预测与试验结果较吻合。
(2)对传动轴材料42CrMo及其具有3Crl3电弧喷涂涂层的疲劳寿命研究表明,涂层越厚,疲劳极限越差,对寿命的影响越深,预测误差越大。同时可通过涂层结合强度对疲劳模型进一步修正。
(3)传动轴再制造后疲劳寿命计算以及疲劳试验结果说明预测相对保守,这不但对传动轴的设计和优化有一定的意义,也说明采用“加材料”即电弧喷涂3Crl3的方式的再制造传动轴,其寿命是可靠的,可直接利用。
[1]Kandil F A,Brown M W,Miller K J.Biaxial low -cycle fatigue of 316 stainless steel of elevated temperature[J].The Metals Society,1982,280(2):203-210.
[2]尚德广,姚卫星,王德俊,等.基于剪切形式的多轴疲劳寿命预测模型[J].机械强度,1999,21(2):141 -144.
[3]徐斌士.再制造工程基础及其应用[M].哈尔滨:哈尔滨工业大学出版社,2005.
[4]张国庆.零件剩余疲劳寿命预测方法与产品可再制造性评估研究[D].上海:上海交通大学,2007.
[5]高镇同.疲劳性能测试[M].北京:国防工业出版社,1980.
[6]徐世文,董满生,胡宗军,等.42CrMo钢疲劳试验研究[J].合肥工业大学学报:自然科学版,2008,31(9):1506 -1508.
[7]王潍.42CrMo钢疲劳短裂纹演化行为及疲劳寿命预测研究[D].山东:山东大学,2008.
