基于神经网络的主轴热误差补偿技术研究

2012-09-26岳红新李国芹

制造技术与机床 2012年3期

岳红新石岩李国芹

(①河北工程技术高等专科学校电力工程系，河北沧州 061000;②天津大学机械学院，天津 300072)

在加工中心的各项误差中，热误差是最大的一项，占总误差的40% ～70%［1］。机床热误差已成为世界制造业关注的焦点。由于机床热边界的不确定性和传热的复杂性，热误差的研究长期以来一直处于定性研究阶段。主轴系统是加工中心机床的最重要部件之一。随着机床转速的提高，切削进给速度的加大，机床发热急剧上升，使得主轴系统产生较大的变形，容易引起振动，不仅降低加工精度和表面质量，还会使齿轮等传动部件和轴承因不能均匀受力而恶化工作条件。因此，主轴系统的变形对机床的加工精度、表面质量都有很大的影响［2］。

本文以MAKINO立式加工中心为研究对象，实测出了主轴系统的温度场和各项热变形，建立了神经网络模型。此模型为加工中心的改进设计、温度控制和误差补偿提供了理论依据。

1 实验与测量

MAKINO加工中心如图1所示。机床的热变形主要表现为:主轴的热膨胀;主轴箱的热变形;立柱的倾斜;床身受热变形;X、Y、Z轴滚珠丝杠的热伸长等［3］。考虑到机床在机加工时，主要运动部件是主轴，所以热变形误差主要以主轴部件产生的热误差为主。

1.1 测温点的布置与选择

通过布置大量测温点来研究MAKINO三轴加工中心的热特性，以及热特性和具体结构间的关系。根据MAKINO立式加工中心的结构和热源分布特点，考虑了以下几点:①由于主轴热误差综合受到床身、立柱、主轴箱和主轴变形的影响，所以有必要同时监测它们的温度变化情况。②因为热传导需要时间，所以一个部件上要有靠近热源和远离热源，或者位置适中的温度传感器，以便及时、真实地反映该部件的变形情况，不至于超前和滞后。③对于主轴和主轴箱，主轴前、后轴承摩擦和主轴电动机是主要热源;对于立柱，主要热源是Z轴进给伺服电动机，因为该伺服电动机具有制动功能，其制动部分的线圈始终有电流通过，因此不断有热量产生并传导到丝杠轴承上;对于床身，热量来自于立柱、X、Y轴进给电动机、导轨、丝杠和大气环境等。因此，我们在机床上安装了14个温度传感器，其位置如表1所示。

表1 温度传感器布置

1.2 主轴热误差的测定

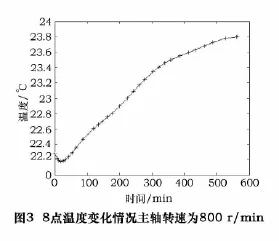
针对主轴热误差，采用传统的5点法测量主轴热伸长、热倾斜和热漂移，坐标系见图2［4］。整个测量过程为:主轴在冷态下启动，以设定转速进行运转，此后每隔一定时间测量一次主轴相对于工作台的热变形，并在测量热变形的同时记录各测温点对应的温度。测温点8的温度变化如图3，主轴Z向误差曲线如图4。

2 神经网络建模

主轴热变形是一个随温度变化的非线性时变过程，因神经网络具有大规模并行性、冗余性及本质的非线性等特点［5］，故采用神经网络的方法建立其模型。

径向基函数神经网络是一种局部逼近的神经网络，它通常选取高斯(Gaussian)基函数作RBF基函数。RBF神经网络具体结构如图5。这种神经网络的特点是网络只对输入空间一个局部领域中的点，才有少数相关连接权发生变化，每次训练中只是修正少量连接权，且可修正的连接权是线性的，故其学习速度极快，并且可保证权空间上误差超平面的全局收敛特性［6］。

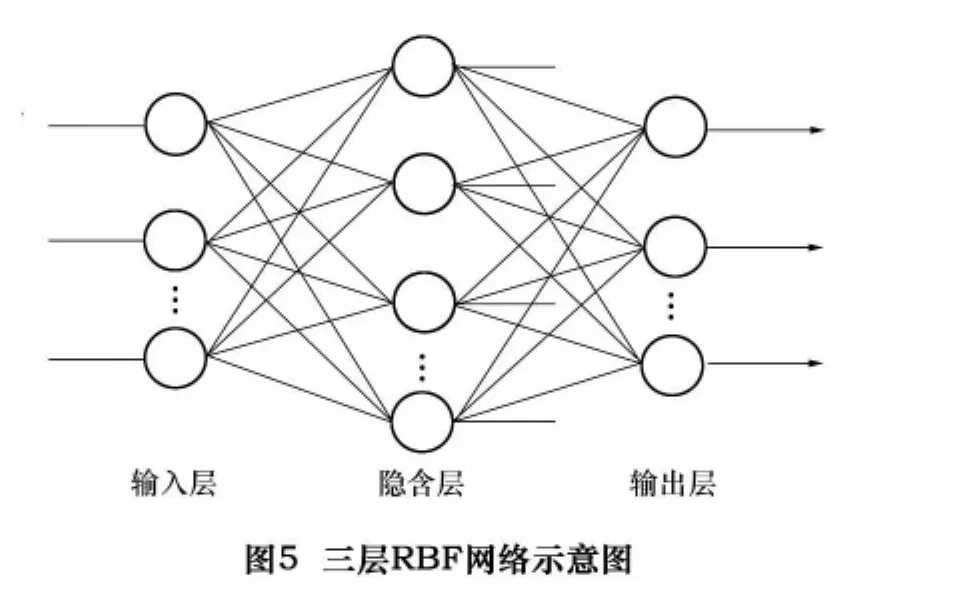
本文采用了1个三层的RBF神经网络来建立主轴热误差的模型。模型的输入为14个温度传感器测量的温度变化值，输出为5点法测量的主轴的热误差。在误差补偿技术研究中，机床温度是缓慢变化的，热误差的数量级是μm级［7］，因此在学习样本前，误差指标设为纳米(0.01 μm)级。训练中网络通过反复不断地增加隐层神经元个数来逼近系统函数，最终达到误差指标时，所用神经元的个数为28个。实验证明RBF学习速度快，逼近精度高。经样本学习和训练后，其结果如图6所示。