带金属接头的复合材料壳体内压变形分析①
2012-09-26崔向斌丁文辉
崔向斌,陈 怡,秦 谊,丁文辉
(1.中国航天科技集团公司四院41所固体火箭发动机燃烧、热结构与内流场国防科技重点实验室,西安 710025;2.西安航天信息研究所,西安 710025)
0 引言
纤维缠绕壳体具有比强度高、比模量大、结构可设计性等诸多优点,被广泛用于固体火箭发动机。目前,关于纤维缠绕壳体承载性能方面的网格理论和复合理论已较完善,非线性的数值方法也可模拟纤维缠绕壳体的结构和缠绕角度。陈汝训[1-2]给出了复合材料壳体圆筒轴压的计算公式,用正交异性薄壳理论分析了复合材料壳体的变形,得到了内压作用下圆筒和封头的应变和位移表达式;分析了纤维缠绕壳体封头低压破坏的原因及3种破坏模式,给出相应破坏模式的强度校核公式[3]。Joon-Hong[4]采用 ANSYS 软件的 APDL语言,实现了参数化的纤维缠绕压力容器非线性分析。崔昭霞[5]建立了纵向和环向共40多层交替缠绕发动机壳体2-D模型,获得壳体在内压过程中的变形。Jae-Sung[6]采用有限元法,研究了 φ250 mm 纤维缠绕壳体缠绕角的变化规律,并对内压载荷作用下的壳体进行了数值分析。许贤泽[7]采用非线性有限元迭代算法,对复合材料壳体的层间应力进行分析,提出了复合材料壳体层间应力分布对复合材料实际结构破坏的影响。
网格理论[2]虽然给出了椭球封头的应变理论公式,但由于封头是变厚度的,无法准确给出封头的弹性模量和泊松比的函数关系。因此,不易准确给出封头的变形计算结果。很多学者也采用数值方法分析了纤维缠绕壳体的位移特性,但都以直径小于1 m的纤维缠绕壳体或2-D模型为主。本文采用复合理论,建立了某φ2 m纤维缠绕壳体的变厚度封头3-D模型,对带金属接头的纤维缠绕壳体封头的变形特性进行了数值分析。
1 计算模型
1.1 实体模型
本文采用有限元法[8],应用 ANSYS软件进行分析,纤维缠绕壳体采用shell46层合单元,金属接头和堵盖采用solid185实体单元,建立某带金属接头的φ2 m纤维缠绕壳体模型。分别建立前后封头从赤道面位置起始的计算模型,前后封头为1.7∶1的椭球封头,前后接头处为堵盖,为了模拟实际缠绕状态,采用壳体解剖数据确定封头任意位置的纤维厚度,建立封头的变截面缠绕模型,见图1。
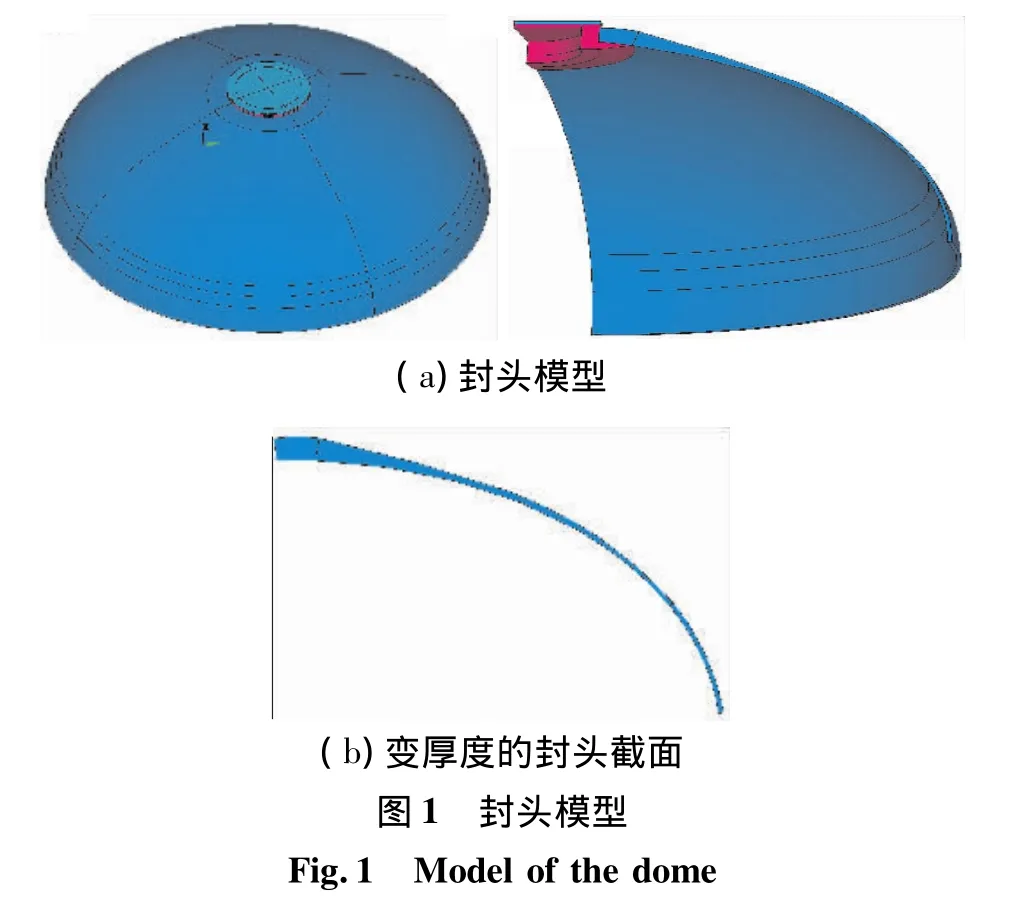
计算中采用复合理论,对纤维缠绕壳体封头进行模拟,根据由纤维材料和基体材料复合得到的单层板材料性能参数,通过定义不同位置每层纤维的厚度和缠绕角度的方法,最后模拟出由实际缠绕方式确定的环向层和纵向层复合而成的壳体封头部分材料,采用的单层板试验性能参数和金属材料性能参数见表1。
1.2 边界条件
有限单元模型见图2,建立以接头为中心的柱坐标系,R、θ分别为径向和切向,Z为壳体的轴向。模拟封头的内压状态,约束前后封头赤道面位置3个方向的位移和转角,在封头内表面施加分布压力。
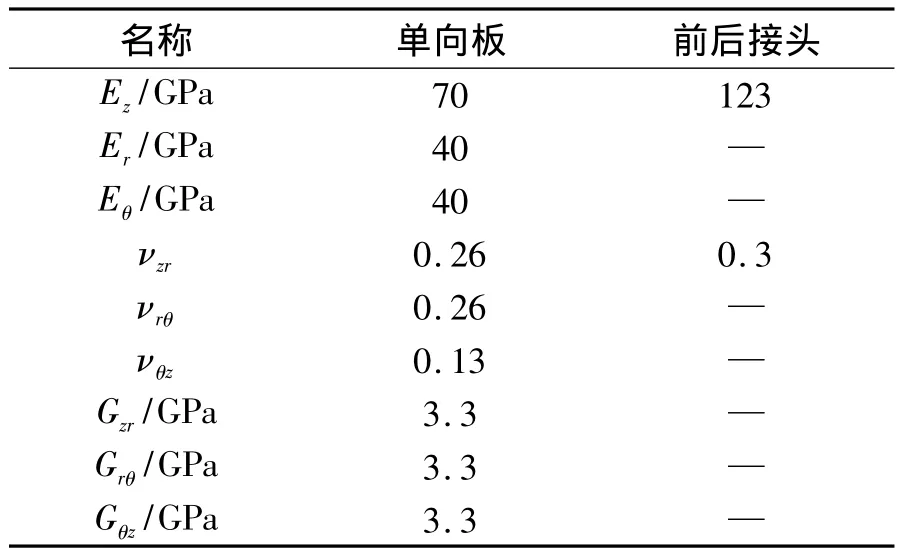
表1 有限元模型材料参数Table 1 Material parameters for FE model

2 计算结果及分析
对前后接头和堵盖采用双线性弹塑性本构关系[9],分别得到前后封头在内压作用下的变形结果。前后封头θ向位移绝对值小于0.3 mm,以R向和Z向为主。因此,重点分析前后封头R向和Z向位移结果,见图3和图4。
由于水压试验中在封头的外表面布置位移计,只能测得封头外表面上位移计距离极孔或者裙端面的弧长数值。因此,为了达到对比的目的,将数值计算结果的位置转化为与水压试验一致的表达方式。
根据前封头的位移图,可得出以下规律:
(1)前封头的最大正向位移值为R向和Z向的合位移,其值约为21.8 mm,位置为距离极孔约400 mm的区域。水压试验中在距离极孔约560 mm位置的变形量约为18 mm,计算得到该位置的位移量约为17.5 mm,两个结果是一致的。
(2)前封头在距离赤道面180 mm位置处,表现为内凹变形,内凹变形值最大值达到7.8 mm,并呈4组屈曲波的外压形态。
(3)前封头位移值呈环带分布,与距离极孔的关系是在距离极孔400 mm范围内,位移值随距极孔位置的增大而增大,并在该位置达到最大位移值。之后,位移值便随距离极孔位置的增大而减小。前堵盖位移值约为11.2 mm,远小于前堵盖附近复合材料的位移值。因此,前堵盖相对于复合材料的位移为内凹变形。

根据后封头的位移图,可得出以下规律:
(1)后封头的最大正向位移值约为R向和Z向的合位移,约为30.4 mm,位置为后堵盖区域。实际水压试验中在距离极孔100 mm位置的位移值约为23.06~25.21 mm,计算得到该位置的位移值约为26.5 mm,两个结果是一致的。
(2)后封头在距离赤道面130 mm位置处为内凹变形,内凹变形值最大值达到12.8 mm,远大于前封头的内凹变形值。
(3)后封头的位移值呈环带分布,随距离极孔位置的增大而减小,在极孔附近区域和堵盖处达到最大位移值,在赤道线位置出现最大负位移值。
结合水压试验得到的位移数据,得到后封头距离极孔长度-水压试验位移和距离极孔长度-数值分析位移的关系曲线,见图5。
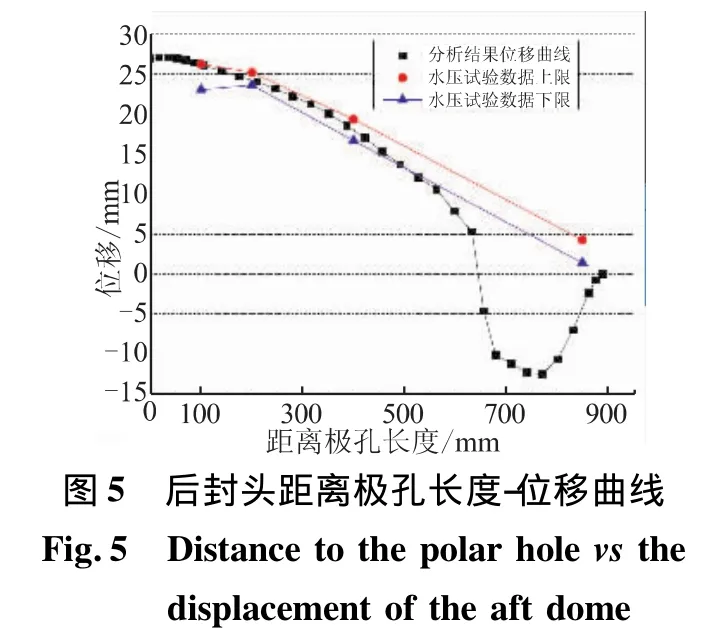
图5表明,后封头的数值分析位移值与水压试验位移值的变化趋势基本一致,且数值基本处于水压试验位移值的上下限内。在距离极孔650~850 mm范围内,分析结果与水压数据不一致,是由于水压试验中,在该位置未采集变形值。实际水压试验中,某φ830 mm相似壳体水压后,在裙端面附近出现白斑,这是由于该位置出现封头内凹造成的。
根据数值分析结果,得到前后封头距离极孔长度-位移曲线,见图6。
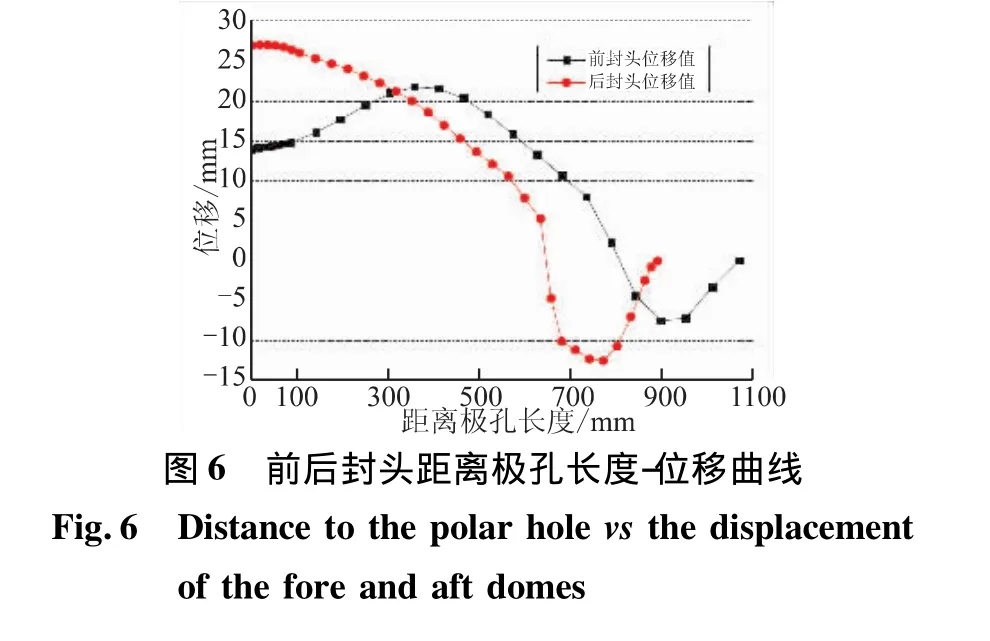
图6曲线表明,前后封头位移值的变化规律是不同的,后封头最大位移值出现在后堵盖处,而前封头最大位移值出现在距离极孔400 mm位置,而非前堵盖处。前后封头虽然采用了相同的缠绕结构,但在位移的变化趋势上却显示出不同的规律。在水压试验中,前封头在距离极孔约300~500 mm范围内发生最大位移值,前堵盖的位移值相对于该范围内的位移值是向内收缩的。
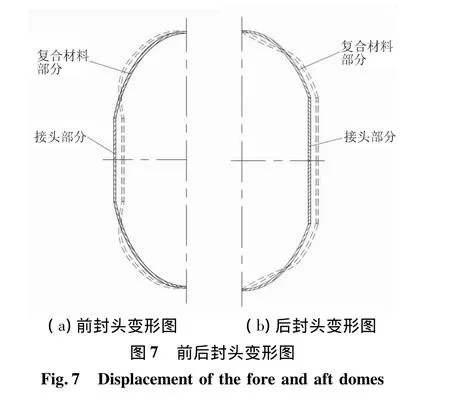
前后封头不同的位移模式是由于不同的开口尺寸造成的,如果将堵盖和接头作为整体考虑,将封头的复合材料作为另一部分考虑。对于前封头,接头部分的尺寸较小,所受载荷及相应的变形值也较小。因此,前封头的变形应以复合材料受内压变形为主,复合材料部分将向外拉开。由于变形协调,整体封头的变形将趋于最小的体积增量,且封头的总伸长量也将趋于最小,因此在接头部分将向回收缩,见图7(a)(虚线为封头变形后的位移形式)。对于后封头,接头部分尺寸较大,所受载荷及相应的变形值较大。因此,后封头变形应以接头部分的内压变形为主,后接头部分向外张开。由于变形协调,整体封头的变形将趋于最小的体积增量,且纤维缠绕部分的总体伸长量也将趋于最小。因此,在赤道面附近的复合材料部分将向回收缩,见图7(b)。分析结果表明,在后封头距离赤道面约130 mm处,后封头发生很大的内凹变形,其位移值约为12.8 mm。
3 结论
(1)前后封头不同的位移模式是由于不同的开口尺寸造成的。开口尺寸较小的接头部分将向内收缩;开口尺寸较大的接头部分将向外伸长。
(2)前封头以复合材料部分的内压变形为主,在距离极孔约400 mm位置处发生最大位移,而前堵盖和前接头由于变形协调表现为收缩。
(3)后封头以后接头金属部分的内压变形为主,在后堵盖和后接头处发生最大位移,而在距离赤道面附近的区域,由于变形协调表现为收缩趋势,显示为类似4个屈曲波形态的内凹变形,其内凹变形远大于前封头的内凹变形值。
(4)对抗压性能较低的带金属接头复合材料壳体,其封头的内凹变形处就是壳体薄弱区之一。因此,在设计及成型过程中应特别关注。
[1]陈汝训.复合材料壳体的轴压稳定性[J].固体火箭技术,2001,24(1):13-15.
[2]陈汝训.固体发动机复合材料壳体变形分析[J].固体火箭技术,2006,29(4):266-268.
[3]陈汝训.炭纤维壳体封头设计的几个问题[J].固体火箭技术,2009,32(5):543-547.
[4]Joon-Hong Park,Chul Kim.An integrated CAD/CAM system for CNG pressure vessel manufactured by deep drawing and ironing operation[J].KSME International Journal,2004,18(6):904-914.
[5]崔昭霞.纤维缠绕壳体应力变形及损伤研究[D].哈尔滨:哈尔滨工程大学,2003.
[6]Jae-Sung Park,Chang-Sum Hong.Analysis of filament wound composite structures considering the change of winding angles through the thickness direction[J].Composite Structures,2002(55):63-71.
[7]许贤泽.纤维缠绕复合材料壳体设计方法及其理论研究[D].武汉:武汉理工大学,2002.
[8]张波,盛和太.Ansys有限元数值分析原理与工程应用[M].北京:清华大学出版社,2005:337-361.
[9]王震鸣.复合材料力学和复合材料结构力学[M].北京:机械工业出版社,1991:71-80.
