金属材料表面涂层损伤的非线性超声评价①
2012-09-26税国双汪越胜
税国双,汪越胜
(北京交通大学力学系,北京 100044)
0 引言
表面涂层技术越来越广泛地用于国防、航空、航天等领域,如固体火箭发动机中的密封层、防热涂层。但由于涂层与基体材料不同,难免存在涂层与基体材料的局部分离、剥落,从而影响涂层的使用性能。又如在固体火箭发动机的生产过程中,为保证推进剂与绝热层或壳体牢固地粘接在一起,在两者之间设计了过渡涂层。为了保证固体火箭的使用性能,要求这一过渡涂层与基体材料间的界面粘接牢固可靠,并要求在长期的贮存后涂层性能仍满足使用要求[1-2]。因此,需要一定的技术手段对上述涂层的性能状况进行检测。目前,超声无损检测技术获得了广泛的应用。虽然在固体火箭发动机的超声无损检测中,已经可实现对于各界面完全空气脱粘类缺陷的检测,但对界面中存在的弱粘接缺陷及涂层内部出现的损伤,目前仍无特别有效的检测方法。
近年来的研究表明,表面涂层的损伤及涂层与基体材料间的界面粘接状况与超声信号的非线性效应密切相关[3-5]。随着表面涂层内部及涂层与基体材料间的粘接界面损伤的产生和演化,单一频率的超声波在传播时,由于材料的非线性将产生高频谐波,即2倍、3倍等整数倍频率的高阶谐波[3]。本文利用Rayleigh波对AZ31镁铝合金试件表面的镍合金涂层在拉伸载荷作用下的损伤演化进行非线性超声无损评价研究,以期对该技术在固体火箭结构中涂层损伤检测的工程应用积累一些基础知识和技术。
1 Rayleigh波的非线性系数
设Rayleigh波沿半空间自由表面的x方向传播,其中z坐标指向半空间物质的内部。纵波和横波的位移势函数为


在具有弱二次非线性的材料中,Rayleigh波传播一定距离后,其二次谐波可近似表示为

对各向同性的材料来说,由于其三阶弹性常数的对称性,只有纵波与高阶Rayleigh波有关。因此,在自由表面附近,Rayleigh波中基频位移ux(ω;x,z)和倍频位移ux(2ω;x,z)之间的关系与纵波的对应关系一致。Rayleigh波的基频和倍频幅值满足:

其中,β为Rayleigh波中纵波成分的非线性系数;x为Rayleigh波的传播距离。于是,由式(4)、式(6)和式(7)可得在z=0的自由表面Rayleigh波基频与倍频的位移关系。进一步可得Rayleigh波的非线性系数为

2 非线性超声试验装置与实验方法
2.1 试验装置
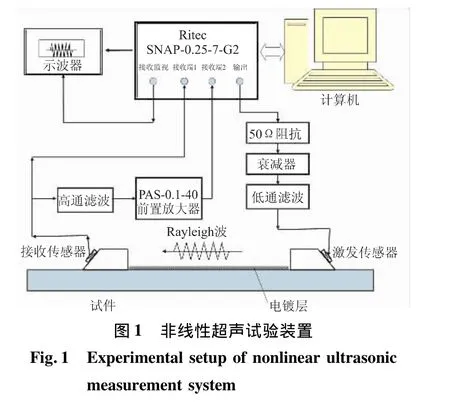
利用Rayleigh波进行金属材料表面涂层损伤测试的试验装置如图 1 所示。利用 Ritec SNAP-0.25-7-G2非线性超声测试系统主机产生16个周期、频率为2 MHz的正弦脉冲串超声信号,该信号经过50 Ω的阻抗匹配、衰减器和低通滤波器后,激励粘接在有机玻璃斜楔上的铌酸锂(LiNbO3)晶片换能器,从而在试件表面激发Rayleigh波。在另一端,同样利用铌酸锂晶片换能器和倾角相同的有机玻璃斜楔接收Rayleigh波,接收超声信号的铌酸锂晶片换能器中心频率为4 MHz。测试中,采用常规医用超声耦合剂对有机玻璃斜楔和金属试件进行耦合。
由于接收到的Rayleigh波信号中,二次及以上的高次谐波一般都很微弱,所以将接收到的超声信号的一路直接接入非线性超声测试系统的主机Input 1端,另一路信号经高通滤波、前置放大后接入非线性超声测试系统的主机Input 2端。将主机接收到的两路信号选取不同的增益,对接收信号中的低频、高频信号成分进行不同程度的放大,从而便于探测接收信号中微弱的高次谐波成分。
2.2 Rayleigh 波的激发
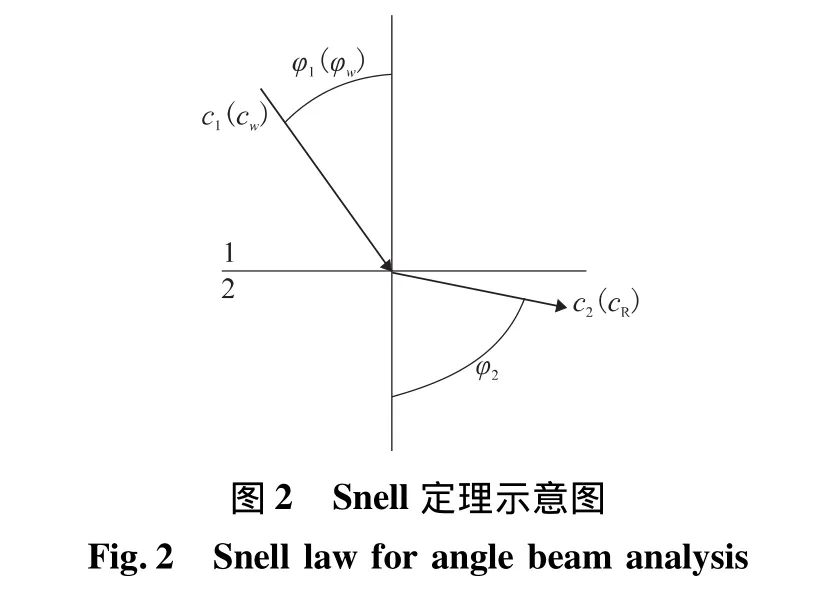
在实际应用中,可利用多种不同的方法激发Rayleigh波,常见的方法有斜楔法和叉指换能器法。利用斜楔法激发Rayleigh波的原理为超声换能器激发的纵波,通过斜楔入射至半无限大的固体介质表面,根据Snell定理:
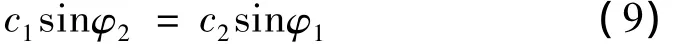
其中,c1为斜楔材料的纵波波速;c2为试件材料的Rayleigh波波速;φ1和φ2分别为入射角和折射角,如图2所示。在试件中激发Rayleigh波的条件是φ2=90°。因此,斜楔中的纵波入射角为

由于固体介质的Rayleigh波波速比纵波波速小,所以产生Rayleigh波的必要条件是试件材料的纵波速度要比斜楔材料的纵波速度大,才能保证sinφR≤1,从而有效地在试件中激发出Rayleigh波。一般采用有机玻璃作为斜楔的材料,其纵波波速为cw=2 670 m/s。于是,根据斜楔和试件材料中的Rayleigh波波速,就可确定斜楔的倾角φ。根据本文实验中选取的材料,可确定斜楔中纵波相应的入射角为65°。
在设计激发Rayleigh波的斜楔时,虽然斜楔的倾角φ是非常重要且需要主要考虑的参数,但最后确定斜楔的其他尺寸时,还需考虑下列因素。由于铌酸锂压电晶片在斜楔中所激发的不是理想的平面纵波,其中只有主瓣的入射角满足激发Rayleigh波的条件。因此,由于旁瓣的入射角不满足Rayleigh波的激发条件,将导致在试件中激发体波,这就会减少试件中所激发Rayleigh波的能量。因此,在确定斜楔的形状尺寸时,应尽量将斜楔中纵波的传播距离缩短。
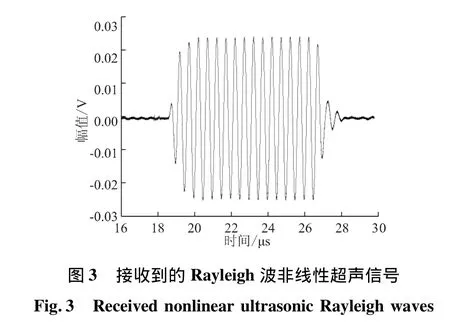
图3所示为利用该方法激发Rayleigh波后接收到的Rayleigh波超声信号。
2.3 实验方法
本文采用的试件为在AZ31镁铝合金表面电镀镍合金涂层,如图1所示。涂层的几何尺寸为长100 mm,宽30 mm,厚度约为0.5 mm;涂层材料的密度为8.9 g/cm3。在实验过程中,首先利用电子万能实验机,将存在涂层的AZ31镁铝合金试件加载到特定的应力后,然后将试件从电子万能实验机上卸下,利用图1中的实验装置激发,并接收Rayleigh波。对接收到的信号加Hanning窗,进行快速傅里叶变换,得到基频幅值A1和倍频幅值A2,如图4所示。为减小实验测试中随机因素的影响(如耦合方式等),保证实验结果准确可靠,对上述测试过程重复3次,每次都将有机玻璃斜楔从金属试件完全移开,然后重新耦合进行测试。

完成上述测试后,再将试件拉伸到大于前一次加载的应力,并再次对从电子万能实验机上卸下的试件进行同样的非线性超声测试,得到试件在本次应力作用后的超声波基频和倍频幅值。重复上述步骤,直到拉应力达到150 MPa左右,涂层局部出现明显的变化为止。图5为试件表面涂层没有明显变化时的情形,图6为试件在拉伸载荷作用下,其表面的涂层局部出现明显变化时的情形。

3 非线性超声测试结果与分析
在图4中,A1和A2分别为压电换能器接收到的Rayleigh波信号基频和倍频幅值,它们分别与式(8)中Rayleigh波的基频位移uz(ω;x,0)和倍频位移uz(2ω;x,0)成正比。因此,在传播距离一定的情况下,Rayleigh波的非线性系数只与A1和A2有关。这里定义并采用如下相对非线性系数[7-8]:

于是,可根据式(11)计算得到Rayleigh波的相对非线性系数β′。记试件未经应力加载时的相对非线性系数为β′0,对试件加载不同应力后的相对非线性系数β′除以β′0进行正则化,最终可得AZ31存在表面涂层的镁铝合金试件的正则化相对非线性系数 β′/β′0(ANP)与应力间的关系。
图7为具有表面涂层的AZ31镁铝合金试件的正则化相对非线性系数β′/β′0与应力间的关系,上述实验数据是在对5个镁铝合金试件进行相同条件的测试基础上得到的。

由图7可看出,正则化相对非线性系数随应力增加而增大。虽然在应力小于150 MPa左右的区间段内,从外观看,试件表面的涂层没有明显变化,但通过实验测试得到的非线性系数随着加载应力的增加而不断增加。由于在不同的载荷作用后,涂层界面会产生一定变化,而本文的实验结果表明了非线性系数随加载应力的变化而变化。因此,通过非线性系数可反映涂层损伤的演化情况,从而达到对表面涂层损伤进行非线性超声无损评价的目的。
4 结束语
本文尝试在不同的拉伸载荷作用下,利用Rayleigh波对金属材料表面涂层的损伤进行非线性超声无损评价研究。结果表明,涂层外观没有明显变化,其非线性系数随加载应力的增加而不断增加。本文下一步工作是进一步研究表面涂层在其他不同载荷(如疲劳载荷)作用下,其性能变化的非线性超声检测。
[1]张以河,孙隆丞,孙维钧.固体发动机复合材料壳体密封隔热涂层研究和应用[J].固体火箭技术,1998,21(1):49-53.
[2]吴宏伟,张广成,张永侠,等.我国固体火箭发动机衬层成型技术进展[J].化学推进剂与高分子材料,2006,4(5):22-24.
[3]税国双,汪越胜,曲建民.材料力学性能退化的超声无损检测与评价[J].力学进展,2005,35(1):52-68.
[4]敦怡,师小红,徐章遂.基于二次谐波技术的固体火箭发动机界面粘接质量的超声无损评价[J].固体火箭技术,2008,31(2):198-200.
[5]邓明晰.层状固体结构表面性质的非线性兰姆波定征方法[J].航空学报,2006,27(4):713-719.
[6]Viktorov I A.Rayleigh and Lamb waves:physical theory and applications[M].Plenum Press New York,1967.
[7]Herrmann J,Kim J Y,Jacobs L J,et al.Assessment of material damage in a nickel-base superalloy using nonlinear Rayleigh surface waves[J].Journal of Applied Physics,2006,99:124913.
[8]Shui G,Kim J Y,Qu J,et al.A new technique for measuring the acoustic nonlinearity of materials using Rayleigh waves[J].NDT & E International,2008,41:326-329.
