钢筋混凝土箱梁沥青摊铺温度场数值分析

邓祖华，刘其伟

(1.江苏建研建设工程质量安全鉴定有限公司，江苏南京 210008;2.东南大学交通学院，江苏南京 210096)

其中包含n个线性代数方程式，从而解出n个节点温度值。

将上述方程组写成矩阵形式，即得到有限元法计算瞬态温度场的基本方程为:

0 引言

热传导问题的数值求解方法主要有差分法和有限元法。其中有限单元法是将一个表示结构或连续体的求解域离散为若干个子域(单元)并通过它们边界上的结点相互联结成为组合体，对每一单元假定一个合适的、较简单的近似解，然后推导求解域的满足条件，从而得到问题的解，这个解不是准确解，而是近似解。下面具体阐述利用有限单元法分析沥青摊铺作用下混凝土箱梁的温度场。

1 混凝土温度场计算基本原理

1.1 导热微分方程

箱梁内部和表面的某一点，在某一瞬间的温度Ti，可以表示为:

该点的温度Ti不仅与坐标 x，y，z有关，而且与时间t有关，对于钢筋混凝土结构可以近似当作各向均为均质、同性的固体，根据Fourier热传导理论，可导得下述三维非稳定导热方程:

式中:λ为混凝土的导热系数，W/m·℃;c为混凝土的比热，J/kg·℃;ρ为混凝土的容重，kg/m3;q为单位体积内放出的热量，J/m3。

当不研究材料的水化热，即q=0时，有:

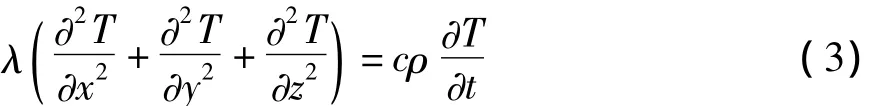
仅考虑平面温度场则:

1.2 初始条件和边界条件的确定

热传导方程建立了物体温度与时间、空间的关系，但满足热传导方程的解有无限多，还应该给出解决这一具体问题解的附加条件，称为定解条件。对于非稳态的导热问题，定解条件有两个方面，即给出初始时刻温度分布的初始条件，以及给出箱梁边界上温度或换热情况的边界条件。

1.2.1 导热方程的初始条件

为准确对沥青摊铺桥梁结构进行分析，取摊铺到试验桥梁前桥梁结构各位置的温度值。

对于平面则:

上式表示的是在初始时刻结构内部温度场分布为其截面坐标的函数或为常数值，与时间参数无关。

1.2.2 导热方程的边界条件

鉴别的时候需要确认鱼腥味的程度、纯净度。鱼粉应该有较为强烈的鱼腥味，但也因原料种类、加工方式及脂肪含量等差别而存在一定的差异，鉴定人员需要鉴别鱼腥味中的细微差异。鱼腥味的纯净度则是指是否含有鱼腥味之外的其他味，非鱼腥味应该越少越好。

导热问题常见的边界条件可以归纳为以下三类:

1)规定了边界上的温度值，称为第一类边界条件，它的表达式如下:

式中:TΓ为物体的边界;Tw为已知的边界温度值，℃;f1(x，y，t)为边界上的温度函数，随位置和时间变化。

2)规定了边界上的热流密度值，称为第二类边界条件。此类边界条件最简单的典型例子就是规定边界上的热流密度保持特定值。对于非稳态导热，这类边界条件可以给出以下关系式:

式中:f2(x，y，t)为边界上的热流密度，随位置和时间变化。

3)规定了边界上物体与周围流体间的表面传热系数β及周围流体的温度Tf，称为第三类边界条件。第三类边界条件可表示为:

瞬态导热时，式中β及Tf均为时间的函数。

1.3 箱梁温度场的非线性有限元解法

采用基于微分方程等效积分原理的Galerkin加权余量法，对热传导平面方程建立微分方程。

1.3.1 有限单元法热传导方程的建立及边界条件的处理

利用加权余量法及格林公式，可得:

式(11)即为平面温度场有限单元法计算的基本方程，对于其中的线积分项，可把边界条件代入，从而满足边界条件。

对于第一类边界条件，上式中的附加线积分项等于0;

对于第三类边界条件，附加线积分项等于

1.3.2 有限单元法的总刚度矩阵的形成

有限元法的计算最终结果是要求出D中的温度分布，把域D剖分成E个四边形单元和n个节点，现在把单元对总体的贡献综合起来，最终把各个节点的温度值求出。

单元总体合成如下:

其中包含n个线性代数方程式，从而解出n个节点温度值。

将上述方程组写成矩阵形式，即得到有限元法计算瞬态温度场的基本方程为:

1.4 温度场的求解

输入各种相关数据，划分单元网格后，依次计算每个单元的热传导矩阵、热容矩阵和荷载列阵，并逐步叠加可形成总的热传导阵[K]，热容矩阵[C]和热传导荷载阵{P}。在时间域上进行有限差分就可以初步迭代计算出每一时刻的温度场。采用向后差分法代入式(13)，化简可得:

输入初始温度场{T}0后，逐步求解式(14)线性方程组，即可求出t时刻各节点的温度值。

2 箱梁温度场的理论计算

ANSYS有限元计算软件热分析模块基于以上理论，本文分别采用第一边界条件及第三边界条件对箱梁截面进行温度场分析。

2.1 第一边界条件求解二维温度场

采用第一边界条件，对测试断面温度场进行分析。沥青表层温度和桥梁结构表面温度用温度枪实测获得。

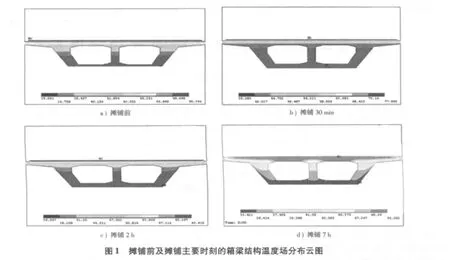
图1为根据荷载步列出的主要时刻的桥梁结构温度分布云图。

根据理论计算结果做出特定时刻的温度梯度曲线，并与实测曲线进行比较，见图2。

从图2可知，理论计算结果与实测数值吻合情况良好，特别是各个测点所达到的最大温度值非常相近，最大不超过0.8℃，可以认为理论分析结果能满足使用精度的要求。

2.2 第三边界条件求解二维温度场

采用第三类边界条件对测试断面温度场进行分析。结合测试断面实测得到的数据和有限元分析结果，对实测值与理论值进行分析比较，以证明理论计算的合理性和正确性，见图3。

从图3可以看出，使用第三类边界条件处理桥梁结构沥青摊铺过程的边界条件与实测结果是吻合的，用第三类边界条件是可以很好地对模型进行分析，并得到正确的结果。

续图3 距梁顶不同距离处的温度实测值与理论值

3 结论

在理论求解定义的初始、边界条件和材料特性热工参数准确的前提下，是可以通过理论计算得到符合实际的箱梁温度场的。

采用第一类边界条件和第三类边界条件对试验桥进行数值分析，两种方法的计算结果均与试验结果吻合程度良好。

［1］王勖成.有限单元法［M］.北京:清华大学出版社，2003.

［2］彦启森，赵庆珠.建筑热工程［M］.北京:建筑工业出版社，1986.

［3］张朝晖.ANSYS8.0热分析教程与实例解析［M］.北京:中国铁道出版社，2005.