基于振动的既有桥梁评估方法的探究

邓国军

(永州市高等级公路管理所，湖南永州 425006)

0 引言

根据试验结果对既有桥梁现貌进行评估，是其检测、评估的重中之重。其评估结果作为既有桥梁养护、修缮和改建工作的主要技术依撑。因而作为既有桥梁桥检测评估及修缮加固中的重要一环，评估技术的研究必定是最重要的。而只有采用卓有成效的手段处理测试结果资料，准确的得到既有桥梁的物理参数以及对既有桥梁的缺损部位、损伤水平的有效评估，进而获取既有桥梁结构的承载能力后才能制定修缮加固的方案。

上世纪最后十年的航空航天领域，普遍采用有限元模型修正技术进行损伤的鉴别，近年来该方法也逐渐应用于土木工程界。

本文在动载试验数据的基础上，采用优化理论对既有桥梁结构进行损伤鉴别，进而依据鉴别结果对仿真模型修正，将修正后的模型用于计算既有桥梁进行承载力，最终达到评估既有桥梁的目的。

1 基本原理

1.1 频率用于损伤评估原理的引入

对桥梁结构采用有限单元法进行离散之后，就将其动力分析化为一个有限自由度的动力系统问题。结构在外荷载作用下，其运动微分方程如下:

其中:［M］、［λ］、［K］分别为结构的质量、阻尼、刚度矩阵;{U}、{U″}、{U'}分别为结构的动位移、速度、加速度列阵。

为简化求解过程，假设［λ］=0，式(1)的解可表达为:

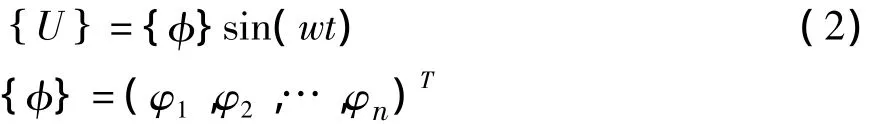
代入式(1)，可将结构动力平衡方程化简为广义特征值问题:

对结构的［M］、［K］引入微小变化［ΔM］、［ΔK］，受其影响，结构的频率和振型w、{φ}也会发生改变 Δw、{Δφ}，代入式(3)运算得:

既有桥梁的加固施工时，所增加的质量与原桥的质量相比一般微不足道，因此可以忽略［ΔM］的影响，则式(4)可化简为:

模态函数关于结构的质量和刚度是正交的，故对相应的广义特征值问题，有:

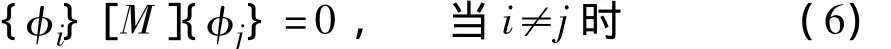
由此推导式(5)并略去二次项的影响得:

对于某一阶模态而言:

如果以［ΔKn］来表示第n个单元发生损伤，则:

式(9)显示了刚度与动力特征值的关系，说明在损伤位置一定时，频率的改变与结构的损伤水平相关。

1.2 结构损伤鉴别的理论分析

要对既有桥梁进行精准的仿真模拟和评估，就必须使理论分析模型与既有桥梁的实际工作状态相吻合，亦即需要修正既有桥梁的有限元模型。首先对既有桥梁裂缝所在截面的截面面积作出假设，进而建立既有桥梁的有限元模型，然后以既有桥梁的实测周期与理论周期差值的绝对值为目标函数，经过相关的优化处理，从而达到有限元模型的修正。这一思想的理论表述为:

假设整体结构通过R这个变量来描绘结构的的损伤，而且损伤也可为物理参数，则:

如果与第i个单元有关的损伤变量为αi，则其单元刚度矩阵可表述为:

式中，K0ei为结构无损时整体坐标系下的单元刚度矩阵;Kdei为结构发生损伤后的相应矩阵。

则发生损伤后的整体刚度矩阵为:

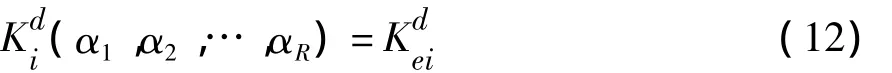
设在荷载试验中实测并采集了前n阶频率。记第i阶实测频率为wmi，与之对应的理论值为wai。模型修正的目标是经过反复调节损伤变量αi(i=1～R)，使得 wai尽量接近wmi。该想法可以表述如下:

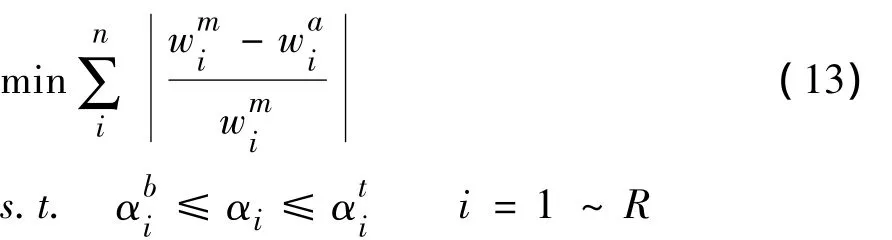
1.3 有约束最优化问题的求解

采用内部惩罚函数法求解有约束的最优化问题(13)过程如下。设不等式约束最优化问题为:

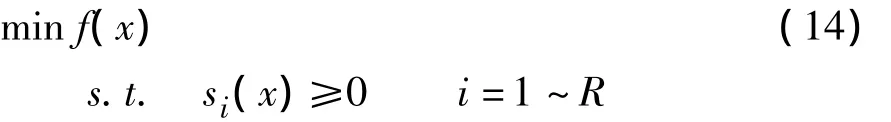
其中，f(x)是目标优化函数;si(x)为约束函数。

建立如下广义目标函数:

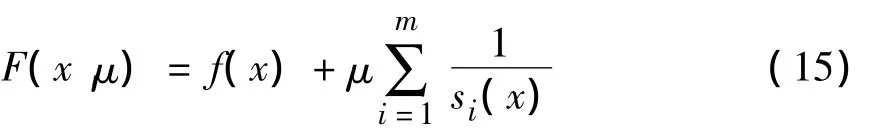
其中μ为惩罚因子，则对问题(14)的求解转化为求解无约束最优化问题(15)。无约束最优化问题(15)的求解已有很多完善的方法，如迭代算法、Newton法等优化算法，大型通用软件如Ansys、Midas等都有优化算法的专门模块。

2 有限元模型的修正

在既有桥梁的实测结果与理论结果间，总是存在一定的差别，造就这种差别有多方面的因素，其中主要因素是物理参数的差异以及结构损伤导致有限元模型的误差。模型修正具体来说就是不断修改模型参数，从而使计算结果与实测结果最大程度的契合。

混凝土的杨氏模量和截面尺寸是桥梁结构的主要物理参数。由于混凝土的老化及钢筋的锈蚀致使构件测量截面尺寸大于实质上的受力截面尺寸，混凝土杨氏模量也随之发生变化。故模型的修正就是校正杨氏模量E及截面的相关惯性矩I，使有限元模型的刚度接近结构的真实状态。

此外，既有桥梁结构的损伤也会致使有限元模型参数选取存在缺陷。结构的损伤基本上是其构件的开裂，因此在计算中可以采用两种办法修正带损伤双曲拱桥模型的参数:

1)拱脚处开裂:其开裂程度应依据结构损伤鉴别的结果，以铰接或半铰接半固接来代替原拱桥计算中拱脚处的固接。

2)拱桥跨中开裂:基于结构损伤鉴别的结果，修正计算模型的两个物理参数。即减小开裂处原模型的杨氏模量或改变开裂处的截面尺寸进而修正截面惯性矩。

本文拟从以下两个方面对模型进行修正:

1)拱轴线的线形直接影响主拱圈截面内力的分布和大小，既有双曲拱桥可能存在着拱轴线形的变化，科学合理地拟合出实际的拱轴线对正确分析双曲拱桥受力起着至关重要的作用。本文拟采用全站仪置于桥位上、下游对拱桥主拱圈进行了线形观测，然后采用样条曲线对测得的离散数据进行了拟合，得到主拱圈线形。

2)由于各种简化和假定，依据竣工图纸建立的桥梁结构有限元模型即无损情况下的模型，其计算结果与试验测量结果之间往往存在不同程度的差别。因此，有必要利用静、动力试验结果优化无损模型中表示边界条件、材料特性等模型性质的参数，使修正后有限元模型的静、动力计算结果与试验测试值的误差在合理的范围内，利用修正后的有限元模型来评估如承载力等桥梁结构的状况。

由于实际结构的模型参数较多，如果将这些参数都作为修正对象，计算量巨大，因此需对这些参数进行灵敏度分析，筛选出灵敏度较大的参数。最终决定需要修正的参数为:主拱圈材质、拱肋杨氏模量、拱上建筑杨氏模量和拱肋间的横向联系。

3 算例分析

以邵阳沿江桥为例，对简单模型，进行单一状态变量的基于周期变化的结构损伤鉴别及模型修正问题的研究，探讨其可行性。

邵阳沿江桥为跨越邵水河的一座桥梁，位于邵阳市区。该桥为2×42 m双曲混凝土拱桥+1×8.0 m实腹式圆弧拱，桥梁全长115.96 m。

桥梁宽度为净-10 m+2×2.5 m(人行道);沿桥横向布置10片拱肋，主桥跨沿桥跨方向设置11道横系梁。拱上建筑采用半空腹式拱式结构，各腹拱圈拱顶设置铰缝以适应拱上结构变形;下部结构采用重力式墩台。主拱拱肋采用27号混凝土(相当于04规范C25)，钢筋采用一级钢筋和二级钢筋。桥梁设计荷载等级:汽-15，挂-80。

采用大型有限元软件Midas进行分析，以空间梁格法来模拟实桥结构，计算模型如图1所示，试验桥跨离散为1 184个节点，2 022个单元。

图1 沿江桥有限元模型

本例中基于结构损伤前后的频率变化，采用最优化方法，成功的获得了结构的损伤值，对下一步的有限元模型修正提供了理论支撑。但研究结果显示该方法也不完美，具体表现在以下方面:无法定位及判定拱肋中发生的不同程度多处损伤，所以必须详尽的对既有桥梁进行外观检查。首先定位结构的损伤位置，且在开始的模型中就模拟多处损伤的同时作用。此外大部分双曲拱桥拱上填料较多，恒载将影响有限元模型的准确度，从而造成计算结果存在较大的误差。

采用有限元分析软件Midas/Civil 2006版对结构进行弹性阶段空间分析，各作用效应分项系数及组合系数均取1.00，主要修改的参数如表1所示。

表1 主要参数及计算信息

修正后的空间有限元模型分析计算结果与初始有限元模型及试验结果对比见表2。

表2 修正后的模型计算对比

通过修正，理论周期与实测周期得到较好的吻合，说明修正后模型的动力特性与结构实际动力特性很接近，模型参数也更接近结构的实际参数。故该方法可以应用于对桥梁结构的有限元模拟中。

4 结论

基于振动损伤鉴别方法是建立于结构动力学基础上的，即把结构离散为由质量、弹性恢复特性、能量耗散特性以及系统的外部扰力组成的动力系统，若结构发生损伤，其物理参数也随之改变，从而致使系统的频响函数和模态(周期和振型等)发生变化，故可将结构模态参量的改变看作损伤出现的标志。通过运动微分方程，推导结构的动力敏感参数与其损伤之间的数学关系，进而实现识别与定位损伤。这充分说明依据桥梁结构自振频率的改变来判定其损伤是有理论依据的。

动载试验基于桥梁结构在外界激励作用下的稳态反应，考虑桥梁的周期、阻尼和振型等模态参数，进而依据稳态反应和模态对桥梁承载能力作出评定，且试验中所测得的桥梁基本参数对其加固设计也是具有实用价值的。

［1］韩大建，王文东.基于振动的结构损伤鉴别方法的近期研究进展［J］.华南理工大学学报(自然科学版)，2003，31(1):91-96.

［2］Pandey A K.Experimental verification of flexibility difference method for10cating damage in structures［J］.Journal of Sound and Vibration，1995(2).

［3］张德文，魏阜旋.模型修正与破损检测［M］.北京:科学出版社，2000.

［4］向天宇，赵人达，刘海波.基于静力测试数据的预应力混凝土连续梁结构损伤识别［J］.土木工程学报，2003(11).

［5］禹丹江.桥梁损伤鉴别的动态方法研究［D］.郑州:郑州大学，2002.