某双菱形塔桥的下塔柱施工过程分析

曾永安，阳东海

(1.浙江永达交通建设工程有限公司，浙江衢州 324000;2.湖南省农林工业勘察设计研究总院，湖南长沙 410007)

0 引言

由于桥梁结构的设计一般是针对成桥状态进行的，对桥梁施工过程结构的受力与变形在设计阶段考虑较少。而大跨径桥梁结构，一般都有一个分阶段施工过程，结构的某些荷载如自重力、施工荷载、预应力等是在施工过程中逐级施加的，每一个施工阶段都可能伴随着徐变发生、边界约束增减、预应力张拉和体系转换等。后期结构的力学性能与前期结构的施工情况有着密切的联系。换言之，施工方案的改变，将直接影响成桥结构的受力状态。在确定了施工方案的情况下，如何分析各施工阶段桥梁结构的受力与变形以确保成桥结构的受力特性及变形与设计的成桥状态一致是非常重要的任务。

在当前计算机高速发展、有限元理论及软件逐步完善的情况下，全桥结构仿真分析技术在桥梁设计理论中掀起了一场革命。有限元分析软件成熟、功能强大及其稳定的计算内核使得其具有广阔的二次开发空间，与此同时，ANSYS在桥梁工程模拟分析中的应用可以代替一些费用昂贵的试验，同时也节省了大量的人力和时间。

本文以混凝土双菱形塔为工程背景，对混凝土塔柱的施工一般均采用分节就地浇注方法施工，每节2～5 m，其方法类似于高墩的施工。由于本文研究的对象是菱形塔，所以施工时尤其需要注意:浇注倾斜塔柱时应计算塔柱自重造成的弯矩，设置足够的横撑，保证倾斜塔的背侧混凝土不受拉，必要时塔柱内需配置施工临时预应力。因此，运用有效的力学分析方法对该桥梁的施工过程进行模拟分析显得尤为重要。

本文主要对该桥双菱形塔下塔柱施工过程进行理论分析与模拟计算，为其施工监控提供有价值的结论。

1 下塔柱理论受力分析

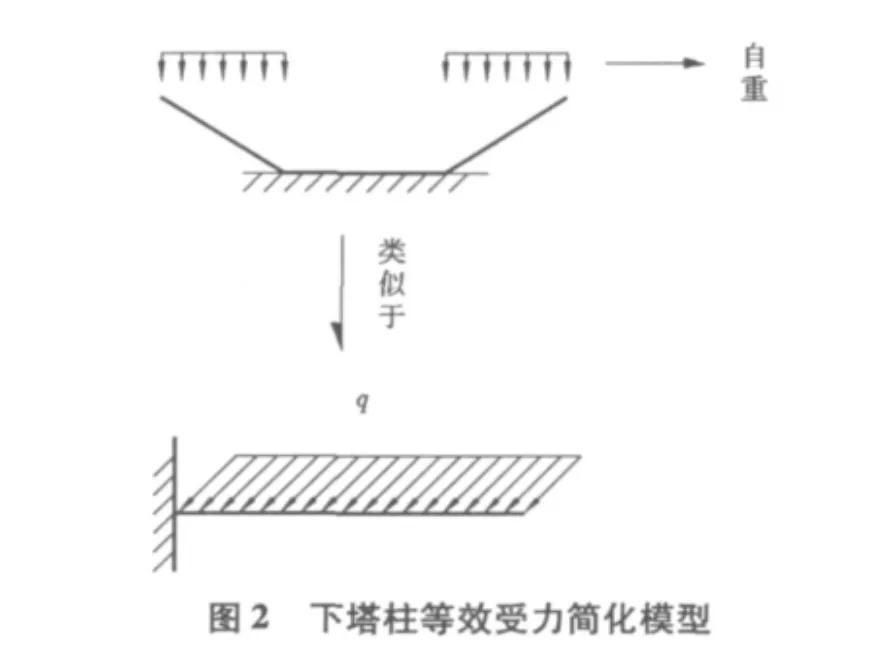
由主塔简化图1，假设塔底位移不变，即塔底与地基固结。加以塔结构为菱形结构，上下塔柱轴线与纵线夹角较大。所以，下塔柱的施工过程类似于悬臂梁的施工过程，下塔柱的简化模型如图2所示。

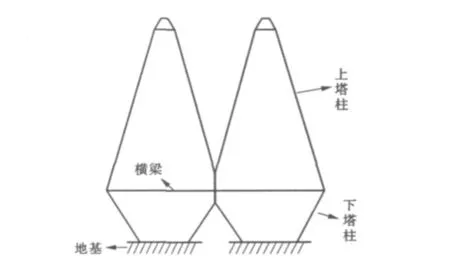
图1 主塔简化图

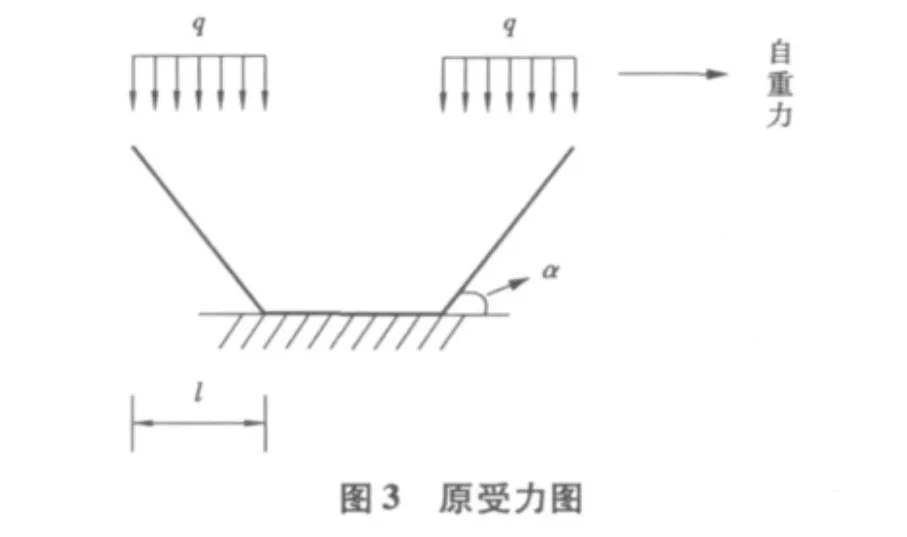
由图2可知下塔柱的受力形式(图3)与悬臂梁的受力形式极为相似。

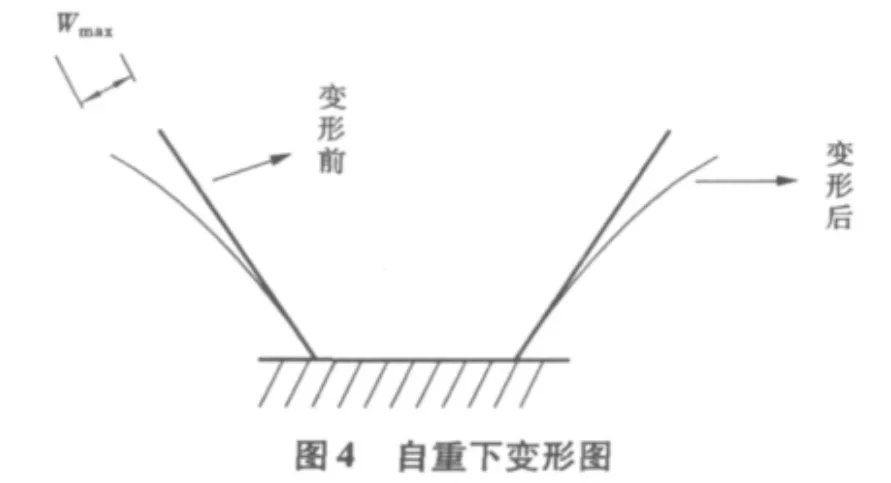
所以，由材料力学和结构力学知识可直接绘出下塔柱在任意施工阶段的变形图(图4)和内力图(图5)。

由于混凝土抗压能力强，自重力沿塔柱轴线方向的分力作用下变形很小，在此简化结构中忽略不计。故由材料力学理论可直接得出下塔柱任意施工段的最大挠度为:

Wmax=ql4/8EIcos3α

由上述下塔柱的内力图及变形图可知:在任意施工阶段，剪力、弯矩和轴力的最大值均处于下塔柱底部的转角处，而最大变形处位于施工中的最顶部。所以，下塔柱在浇注完全时为整个下塔柱施工过程中的最不利工况。此时结构的最大内力和最大变形均达到最大值，而核心截面分别位于下塔柱底部转角处和施工中的最顶部。故在下节的计算机模拟计算中只需验算浇注完全时最大内力和最大变形是否符合施工规范。

计算:

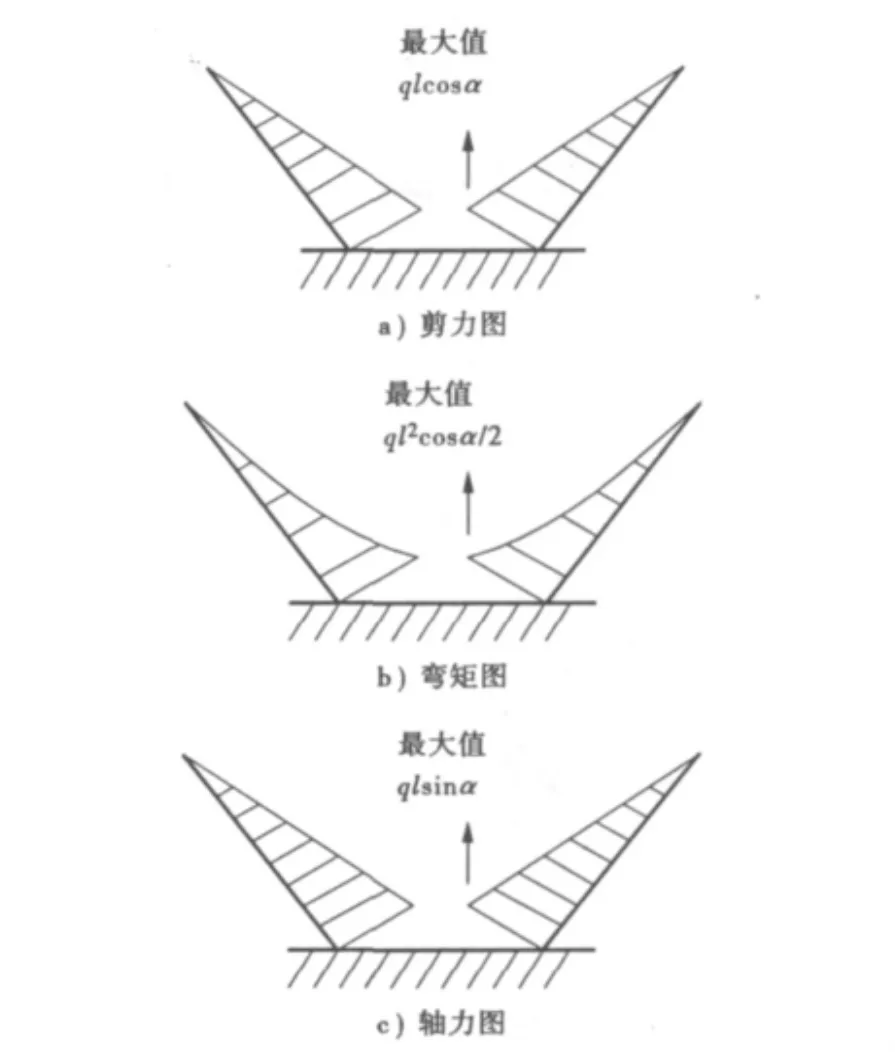
图5 自重下内力图

由该桥设计知以下数据:α≈64°，弹性模量E=3.45 ×1010Pa，混凝土密度 ρ=2 600 kg/m3，I=(bh3)/12=(2.5 m ×5.53m3)/12=35.04 m4，g=9.8 N/s2。则:

cosα =0.434，sinα =0.898。

当浇筑完成后:l≈10.3 m，悬臂段高度 H≈16.549 m。

总重量ql=(bh)×H×ρ×g=5 797 942 N。

由上述内力图和变形图可解得:

最大剪力 Qmax=qlcosα =0.251 6×107Pa;

最大挠度 Wmax=ql4/8EIcos3α ≈1.09 cm。

由于下章ANSYS的三维模型不能模拟求解弯矩，且为了与下章的模拟计算值进行对比分析，故在此求出最大剪力和最大挠度的理论解。

2 下塔柱施工过程有限元模拟分析

上节理论分析中得出下塔柱在施工过程中的最不利工况，本节将对该工况下主塔的内力和变形进行模拟计算，并将各项模拟计算数据与施工规范进行对比分析。

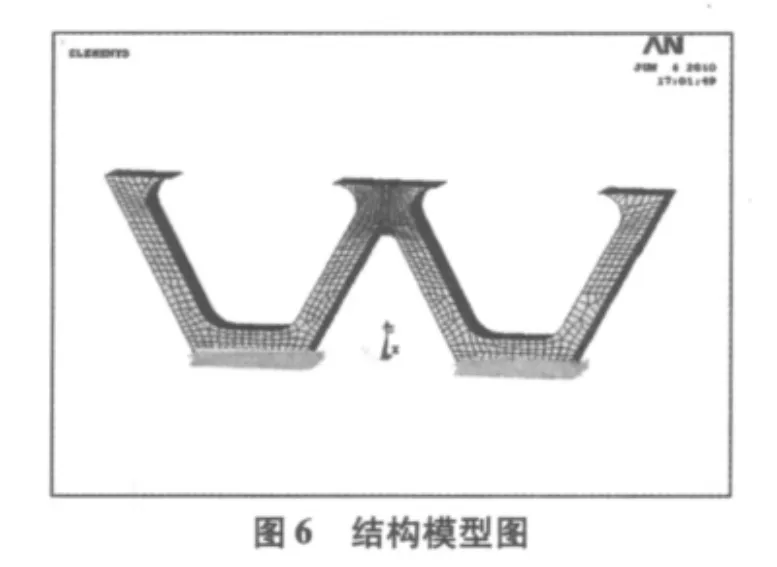
2.1 下塔柱浇注完成

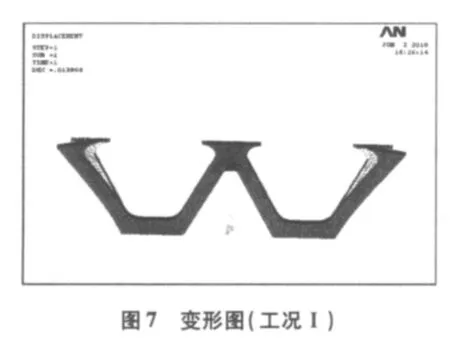
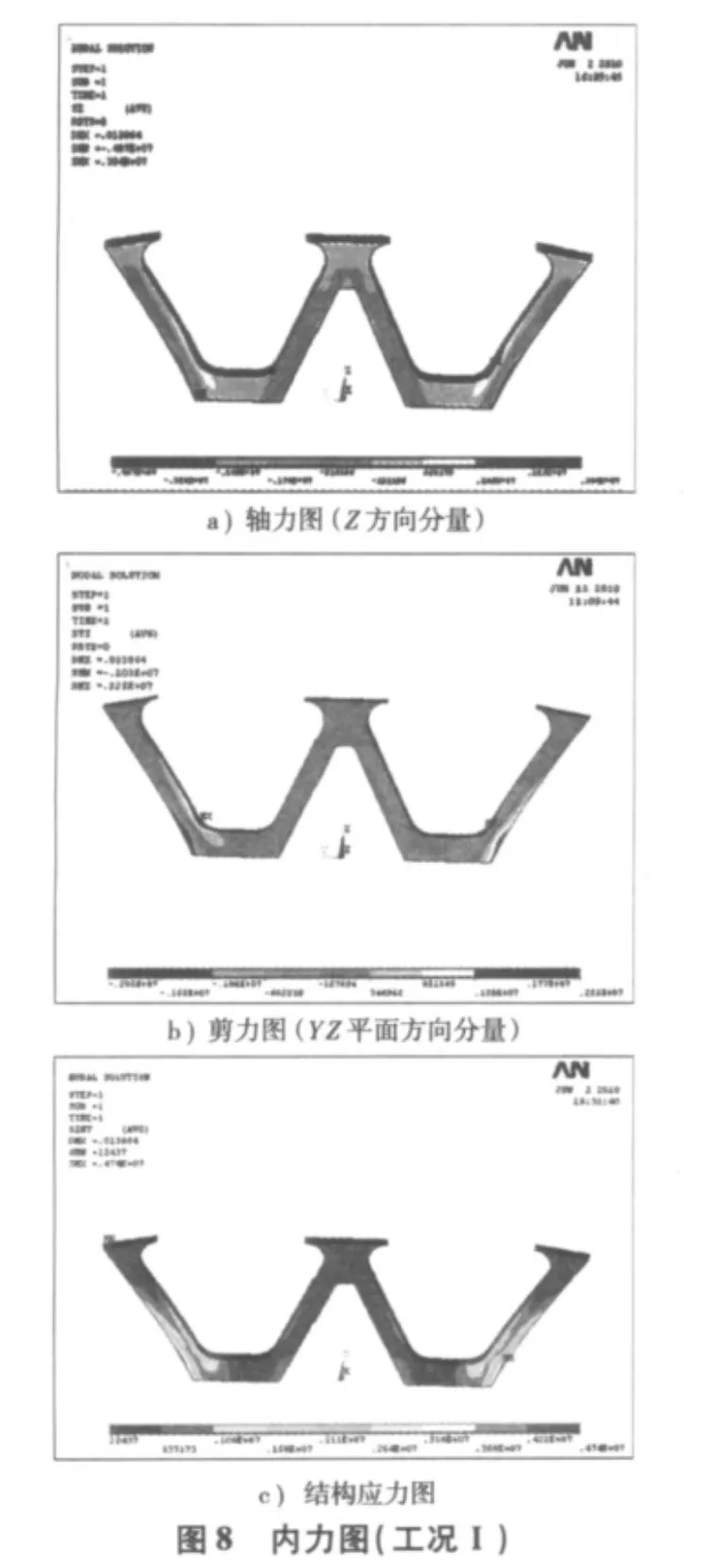
该工况下的ANSYS结构模型如图6，求解得变形图和内力图如图7、图8。

可看到以上变形图和内力图的核心位置与上节理论分析中所描述的位置一致。

实际该特大桥双菱形塔采用C50混凝土，查表可知:

C50混凝土抗拉强度为:2.65×106Pa;

C50混凝土抗压强度为:3.24×107Pa。

此下塔柱高19.549 m，查桥梁悬臂梁施工规范可得悬臂梁的最大施工挠度为悬臂梁长度的2/1 000，可知:

下塔柱的最大位移约为:20 m/500=4 cm。

从以上计算所得的变形图和内力图中可看到此工况下:

下塔柱的最大位移为:1.38 cm＜4 cm;

下塔柱的最大拉应力为:3.04×106Pa＞2.65×106Pa;

下塔柱的最大压应力为:0.474×107Pa＜3.24×107Pa。

计算结构显示此工况下，下塔柱的最大拉应力已经超出了C50混凝土的抗拉强度，故此工况的下塔柱内力不符合施工要求。

2.2 下塔柱浇注完成(施工中施加临时水平推力)

此工况为在上述工况的基础下在左右下塔柱的顶端各施加2个水平向内的水平推力F，以下的计算以F=0.5×106N为例。此工况的实体模型与A一样。

得该工况的结构受力图、变形图、内力图如图9～图11。

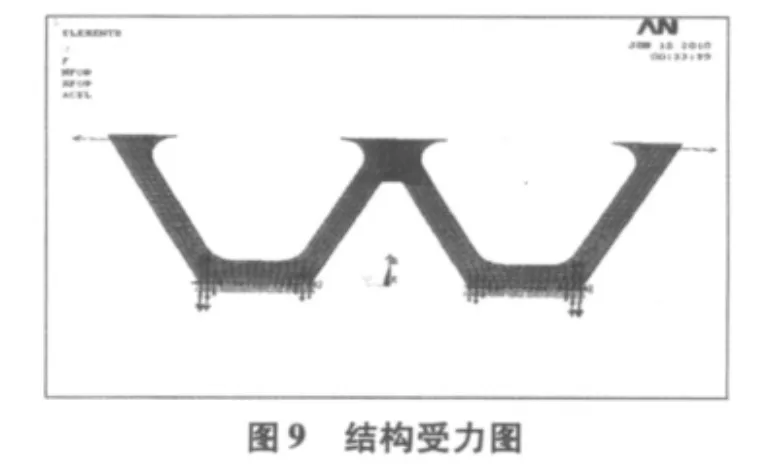
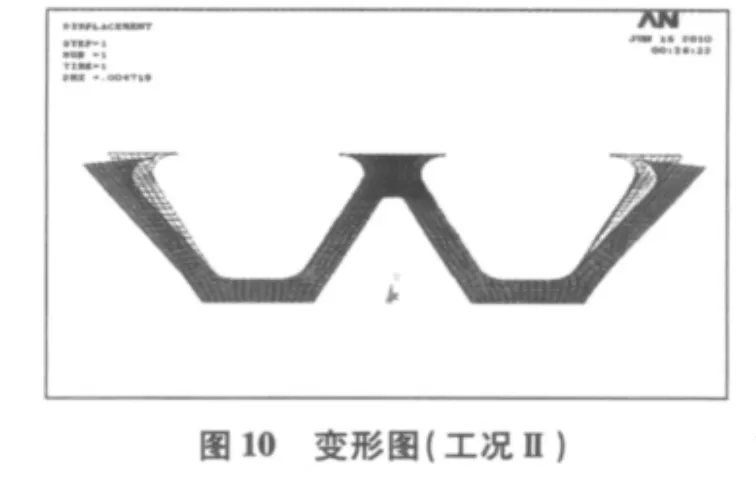
从以上计算所得的变形图和内力图中可看到此工况下(施加顶推力后):

下塔柱的最大位移为:0.67 cm＜4 cm;

下塔柱的最大拉应力为:1.41×106Pa＜2.65×106Pa;

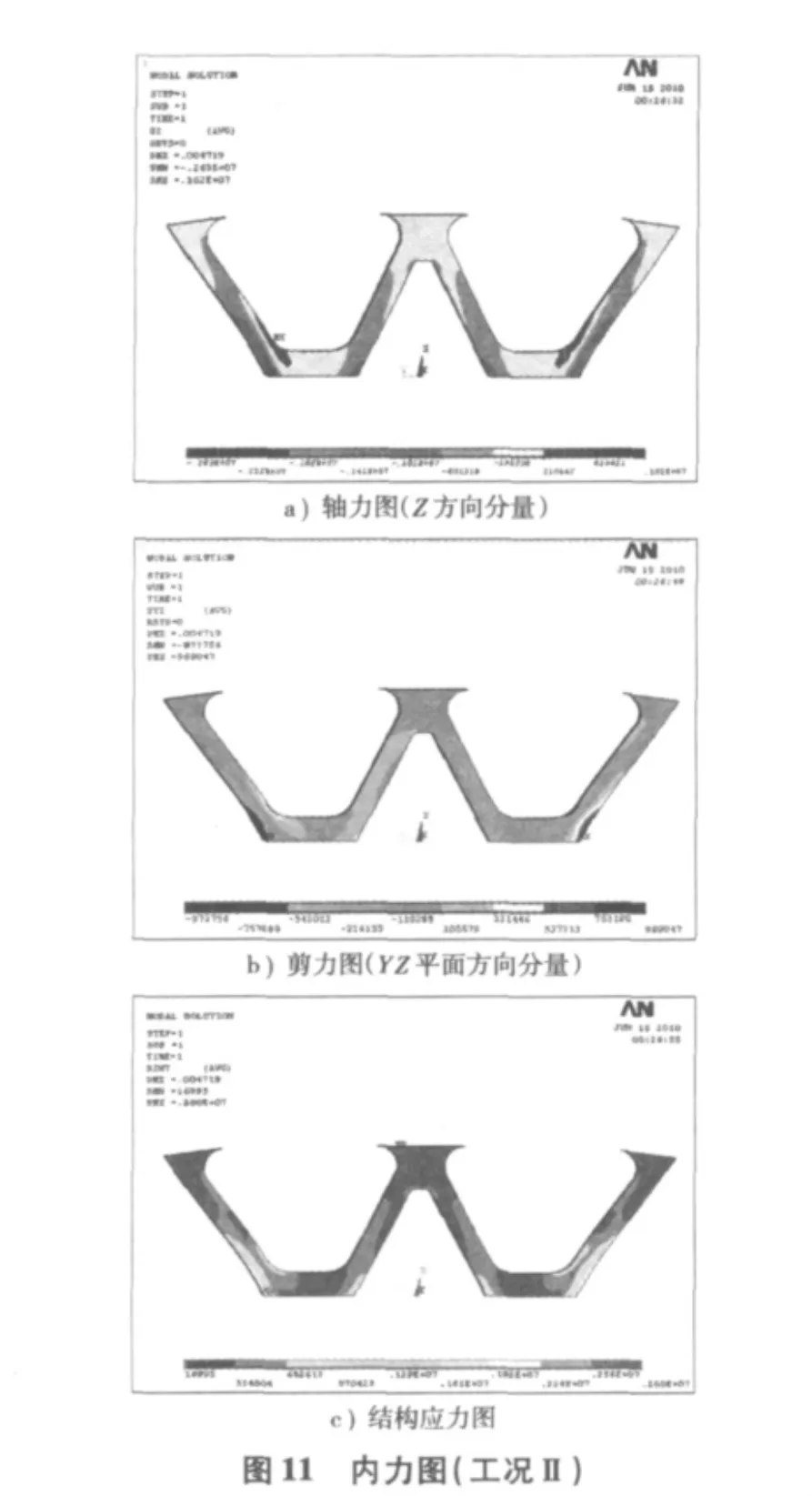
下塔柱的最大压应力为:0.878×107Pa＜3.24×107Pa。

故下塔柱在施加了顶推力后结构内力得到了明显的控制，各项数据均达到了材料的强度限制和要求，此时下塔柱的最大位移更是精确到1 cm内，为下塔柱的闭合成型(横梁施工)打下了更精确的基础。

3 结论

由理论计算和ANSYS模拟计算结果，现取部分数据在此进行对比见表1。

表1 理论计算与ANSYS模拟计算对比

表1中工况Ⅰ的剪力值误差为:

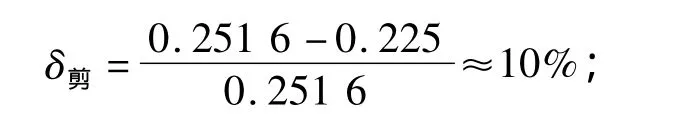
工况Ⅰ的挠度值误差为:

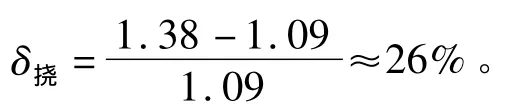
上述误差反映剪力(内力)值的模拟计算误差可控制在10%以内，误差不大。且由图8和图11比较不难发现，两图的剪力值分布规律基本吻合，故由此说明此文建模思路和模拟计算结果具有较高的准确性，参考价值较大。

而挠度值的模拟计算误差则达到30%左右，误差较大。就其原因可能来自于两个方面:①理论计算中结构经过简化后与实际结构模型存在一定的误差;②模拟计算中考虑了0.2的泊松比，理论计算中没有考虑这项数据，也正因此可从表1中看出挠度理论值小于模拟计算值。

通过本次桥塔施工过程的理论分析和模拟计算，得到如下结论:

1)主塔宜采用对称施工。

2)下塔柱为实心结构，施工中由于悬臂产生的拉应力过大，在施加水平推力的情况下各项数据远远小于施工规范的各项要求，为提高施工安全性，需在施工中设置一定的临时水平推力。

［1］官万轶，韩大建.大跨度斜拉桥施工控制方法研究进展［J］.华南理工大学学报(自然科学版)，1999(11):14－19.

［2］廖小雄，黄 艳，郭 奔，等.基于ANSYS的斜拉桥施工过程模拟分析［J］.武汉理工大学学报，2006，30(3):496 －499.

［3］王国强.实用工程数值模拟技术及其在ANSYS上的实践［M］.西安:西北工业大学出版社，1999.

［4］Reddy P，Chaboussi J，Hawkins N M.Simulation of construction of cable-stayed bridges［J］.Journal of Bridge Engineering，1994，4(4):258 －262.

［5］陈爱军，邵旭东.无背索竖琴式斜拉桥混凝土斜塔柱合理结构型式分析［J］.公路工程，2007，32(4):130 －135.

［6］郭木华.基于二分法的斜拉桥施工控制过程参数识别［J］.公路工程，2010，35(3):132 －135.

［7］曹建邦.三塔双索面预应力混凝土斜拉桥施工控制［J］.湖南交通科技，2005，31(1):55 －58.