循环荷载作用下路基土体塑性变形研究

黄 斌，邓秋洪，杨小兰

(1.湖南省高速公路管理局，湖南长沙 410029;2.郴州市公路管理局，湖南郴州 423000)

0 前言

路基沉降是由于路堤和地基固结以及车辆荷载反复作用下引起的累积残余变形造成的［1，2］。随着经济发展，因重载交通运输工具反复作用而产生的路基不均匀沉降问题越来越突出，因此对于重载公路、铁路进行重复荷载作用的累积变形计算要求非常迫切。这个问题也一直是交通运输领域的难题，因为在传统弹塑性力学基础上提出的许多重复荷载作用下土体永久变形进行理论计算方法都很难对重复荷载下岩土发生永久变形的机理进行准确描述，其计算结果也很难全面反映土体变形的基本规律［3，4］，而采用经验公式进行计算既很难适应各地土体的变化以及路基内应力分布的变化，也不符合岩土力学发展的趋势。此外，岩土体的强度变异性是其区别于其他工程材料的显著特点之一，也是现有理论计算方法没有考虑的。

为此，本文在考虑路基岩土材料强度变异特性的基础上，分析循环荷载作用下土体塑性累积变形特征，采用单元强度随机生成的有限元方法模拟了循环荷载下土体塑性累积变形发展规律，开展重复荷载作用下土体永久变形计算数值模拟，并应用该方法对车辆荷载作用下的红层填料路基进行了塑性累积变形计算，得到了红层路基在不同车辆荷载作用下动力变形渐进式发展的规律。

1 土体塑性累积变形计算方法研究

由循环荷载作用而产生的残余应力和永久变形一般可采用以下两种方法来计算:

1)基于循环荷载下土体应力－应变本构模型。把循环荷载处理成一系列静的加载、卸载过程，利用有限元法对加载历史的每一个应力循环分成若干步进行计算，所有的应力循环产生的残余变形之和即为总的永久变形。采用该方法计算路基土变形仅需要将以上某个循环荷载下的土体本构模型应用到数值计算程序中即可，其计算结果的准确程度在很大程度上取决于本构模型的合理性。

2)基于土体塑性累积变形与荷载作用次数关系的计算方法。该方法对路基的变形计算分为三步:①在试验资料的基础上建立土体塑性累积变形与荷载作用次数关系;②通过有限元或弹性理论方法分析得到一个或多个循环作用结束时土工结构物内各区域(层次)的应力状态;③根据这些土体塑性累积变形与荷载作用次数关系分别计算出土工结构物各区域(层次)在确定荷载作用次数下的塑性累积变形，再将各区域(层次)垂直方向的塑性累积变形累加，可得到土工结构顶面各处的塑性累积变形。采用该方法计算的核心是建立重复荷载作用下土体塑性累积变形与荷载作用次数的关系。最早建立这一经验公式的是Barksdale［5］对其三轴试验结果进行了整理得到式(1)的关系:

莫尼斯密斯(Monismith)［6］采用如式(2)形式所示的模型:

马吉德扎德(Majidzadeh)等［7］研究了循环荷载作用下地基土的塑性累积变形特性，提出以下关系:

式中:a、b为回归参数。

该式(3)与式(2)在本质上并无太大区别，这两个模型的有效性为众多试验所证明，也成为对土体变形的基本规律认识的重要成果，之后众多学者所建立的经验公式大多以此为基础。但是对于式(2)模型中最大的不足是没有考虑土样应力状态对其塑性累积变形特性的影响，鲍德(Paute)［8］得到了一个包含荷载作用次数与应力水平在内的永久变形发展模型。同时，塞里格(Selig)［9］则在式(2)的基础上，对参数A的确定进行了研究，认为参数A应与土样所受的动偏应力和静破坏偏应力有关，并得到了确定参数A的经验公式。邱延峻［10］在式(2)的基础上提出了能考虑应力/强度比的计算公式。Chai Jin-chun，三浦(Miura)［11］等在此基础上，提出包括初始静偏应力的更复杂经验公式，并用于汽车荷载作用下路基的塑性累积变形量预测，而且取得了较好的效果。

毫无疑问，采用基于循环荷载下土体本构模型的方法计算交通荷载下路基、地基最终塑性沉降量更为科学，但是在实施过程中是一件很困难的事情。其原因在于:土体在重复荷载作用下的规律是非常的复杂，目前所建立的重复荷载下土的本构模型不但有很多需要试验确定的参数，而且有些参数和关系本身物理意义并不明确，更不能通过试验确定。因此这些本构模型在预测土体在重复荷载作用下的变形的时候显得非常困难。目前尽管现代土力学在土体在重复荷载作用下的本构模型研究取得了长足的进展，但是模型的实用性依然没有得到明显的改善，形成了国内外公路路基土变形计算方法与现代土力学脱节的现象［12］。

数值计算方法是常用的变形计算方法，塑性理论把应变增量表示成弹性应变增量和塑性应变增量两部分之和:

其中，弹性变形按式(5)计算:

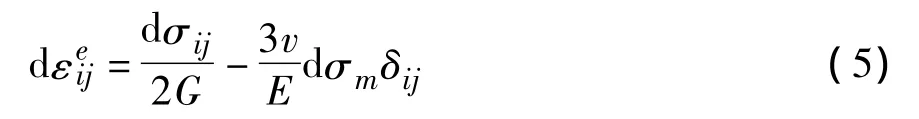
塑性变形部分按式(6)计算:

〈 〉表示一种运算，若dλ ＞0，〈dλ〉=d;若dλ≤0，〈dλ〉=0。

式中K为塑性模量。

一般采用相关流动法则，即Q=F，则有:

不同种变形计算方法的差别主要在于屈服面、破坏准则、硬化规律、流动法则四方面。常用的循环荷载作用下土的累积应变计算方法有两种思路:①基于荷载循环的增量分析方法，通过建立土的非线性的应力—应变关系，将循环荷载被处理成一系列静的加载、卸载过程，利用有限元法对加载历史的应力循环分成若干步进行计算，所有的应力循环产生的残余变形之和即为总的塑性累积应变。②只分析有限元法或其他方法分析一个循环作用的应力，建立土的塑性累积变形与土的初始应力状态，动应力和应力循环次数之间的关系，然后对不同区域采用不同的塑性累积变形与应力循环次数的关系求解其总的塑性累积变形。

2 循环荷载作用下土体塑性累积变形特征

荷载作用是路基产生沉降变形的主要原因之一。路基在自身荷载作用下将产生固结沉降;而运动的汽车对路基产生的重复荷载效应可使路基塑性变形逐渐累计而产生较显著的变形。土体在长期车辆荷载作用下的变形特性研究需要进行长期试验，因此研究的难度比较大，但是出于在公路铁路对路基、路面变形计算的需要，国内外这方面研究虽有所开展，但是成果不多。

在动荷载作用下，荷载较小且作用次数较少时，土体显示出近似弹性体特征，当荷载较大且作用次数较大时，由于颗粒间的相互滑移，形成新的排列，产生压密，出现不可恢复的永久变形。塞德(Seed)［13］通过三轴试验发现土体永久变形随循环荷载增大而增大的特征。巴克斯代尔(Barksdale)［14］对几种粒料的试验发现，在较低的偏应力条件下，土体的塑性变形随着荷载作用次数的增大而减小，而超出一定偏应力后，土体的塑性变形随着荷载作用次数的增大而增大，偏应力越大则永久累积塑性变形越大。希斯(Heath)［15］整理了伦敦粘土试样三轴试验累积应变和荷载重复作用次数关系，发现存在两组试验曲线，一组的变形逐渐发展直到破坏;另一组的变形速率逐渐缓慢最后达到稳定状态(弹性条件)。布朗(Brown)和海德(Hyde)［16］发现循环荷载下土体轴向塑性应变大小和偏应力与固结应力之比直接相关。铁道部科学研究院［17］也对路基土的动力特性做了研究，对路基土永久变形的研究得出:①在低应力水平下，路基土主要表现为可恢复的弹性变形，塑性应变累积很小，与重复荷载次数成半对数关系。②随动应力水平的增大，塑性应变随荷载作用次数增加有较大的增长，但当塑性应变累积达到一定程度后，变形趋于稳定。③当动应力水平继续增大时，试样因塑性变形的急剧增长而破坏，此时塑性应变与重复荷载次数成指数关系。闫澍旺［18］通过对重塑软粘土进行动、静三轴试验，证明在往复荷载作用下，土的变形－强度—有效应力唯一对应关系仍然成立。基于此将累积空隙水应力作为标识，可以将复杂的动力问题模拟成静力问题进行计算。蔡英［19］针对路基填土在列车荷载重复作用下产生永久变形的问题，利用动三轴试验，研究了重复加载条件下，土体的临界动应力和永久应变随加载次数、加载频率和周围压力变化的规律:①重复加载次数与永久变形的试验曲线可分为三类，即衰减型曲线、临界状态曲线、破坏型曲线。临界动应力在某一范围内变动。②重复加载条件下土体的破坏应变不受动应力水平的影响，无侧限时破坏应变为9%。③土体的临界动应力随加载频率提高而逐渐降低，相同动应力水平时，低加载频率的试样更易破坏，相同加载次数时，其永久应变也较高频加载试样的大。④在低围压下，临界动应力与围压近似为线性关系。相同动应力水平和加载次数时，高围压下试样产生较大的永久应变。

循环荷载试验表明，在少量的小荷载作用下，土体一般显示出近似弹性体特征，但是随着荷载作用次数的增加，土体可出现明显的塑性累积变形，以至于会对土工结构的使用性能造成影响，如公路产生的桥头跳车等问题。如果荷载较大，则试样变形随着荷载作用次数增加从而产生破坏。Monismith公式基本适用于土体在循环荷载作用下塑性累积变形的发展规律。

Monismith公式中参数A表示N=1时，即土体塑性在初次荷载作用下变形的大小。土体塑性变形的发展规律主要取决于参数b:当b＜1时，土在每一次荷载作用下的塑性变形随着荷载作用次数的增加而减小，荷载作用次数趋于无穷，塑性累积变形将不再增大，土体最终稳定在弹性状态，即土体由弹塑性体向弹性体过渡。当b＞1时，土在每一次荷载作用下的塑性变形随着荷载作用次数的增加而增大，土体将达到破坏状态。b=1是一种临界状态，土在每一次荷载作用下的塑性变形不随着荷载作用次数变化，土体将在某一次荷载作用时达到由最大容许应变所定义的破坏状态。b值的大小与土的性质、状态、围压大小、循环动应力的大小、频率有关。一般由试验确定。对于同一土体在相同围压下，b值是否大于1取决于循环动应力的大小，研究人员提出在某一围压下b=1时土体对应的循环应力为临界应力σcr，也称该围压下的动强度，当动应力超过σcr时，则塑性变形不断发展，直到破坏;而当动应力小于σcr时，土体塑性变形随振次的增加而趋于稳定。不同土体临界动应力σcr不同，σcr的影响因素包括土的种类、含水量、密实度、动弹性模量、围压大小、荷载波形和作用频率等。σcr随围压的增加而增加，随频率的增加而减小，通常粗粒土σcr比细粒土的大，细粒土的饱和度越低或密度越高，其 σcr越大。

3 基于岩土变异性的塑性累积变形计算方法

现有对岩土在循环荷载下的塑性累积变形研究都是基于岩土材料强度均匀的基础上的，未考虑岩土材料强度的变异性。一般不考虑材料强度随机性的弹塑性有限元法在计算岩土变形时，如果循环荷载较小，则岩土内部任意位置都不会屈服，因此无塑性变形出现，这不符合岩土在循环荷载作用下的变形规律。本文基于岩土变异特性，提出一种新的循环荷载作用下土体塑性累积变形计算的思路:假定岩土体的强度统计符合正态分布，岩土内强度处处不同，这样，既使在较小的循环荷载作用下，岩土体也可能产生一定量的塑性变形;在较大的循环荷载作用下，既使这一荷载产生的应力没有达到岩土的平均强度，也可能导致岩土体产生持续增大的塑性累积变形而破坏，其基本步骤为:

1)建立具有一定数量的单元有限元几何模型;

2)确定材料弹塑性本构模型，本文中采用基于摩尔－库伦破坏准则的理想弹塑性本构模型;按照正态分布特征生成各单元的强度指标，给单元赋值;

3)施加荷载，执行有限元计算，输出塑性累积变形。

在模拟计算中，单元强度随机生成和赋值必须在二次开发子程序中实现，但是MARC有限元程序中虽然包含有摩尔－库伦破坏准则的本构模型，但是利用MARC前处理程序建立的模型，所选用的自带本构模型的各项参数必须在几何建模时赋值，不能在子程序中赋值。因此要实现基于材料强度参数随机生成的数值模拟，须在二次开发中重新编制基于摩尔－库伦破坏准则的理想弹塑性本构模型。

摩尔—库伦屈服准则的表达式为:

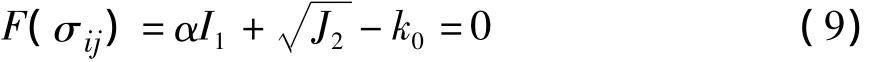
式中:I1为应力张量的第一不变量;J2为应力偏量的第二不变量;α，k0为与材料粘结力c及摩擦角φ相关系数。

因为平面应变条件下式(9)与摩尔—库伦破坏准则完全一致，可导得α，k0的表达式:

由式(8)得:

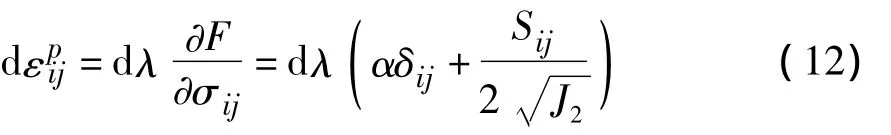
由塑性功增量表达式:

4 计算实例分析

4.1 计算模型验证

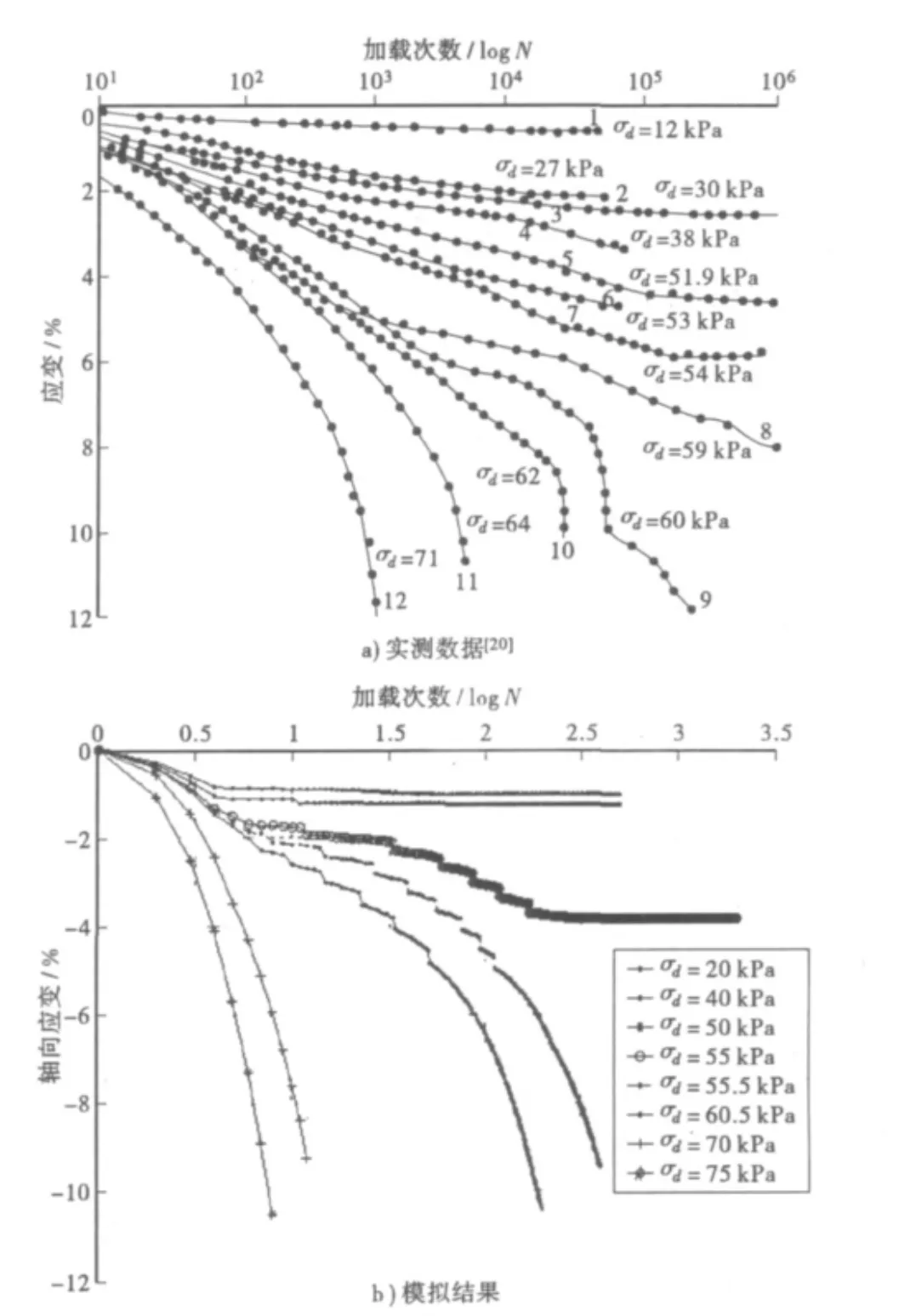
图1 重复荷载下永久变形曲线

为验证本文模型的准确性，采用文献［19］的试验结果进行验算，为采用国产SD—780型和日本产DTC—306型两种动三轴仪对成都粘上进行的循环荷载试验数据。试样含水量为天然含水量(25.6%)。干容重为 1.52 g/cm3，容重为 19 kN/m3，土体静强度指标:c=33 kPa，φ =14°。在无侧限、加载频率10 Hz情况下，采用不同竖向动应力进行循环荷载试验，得到土体累积变形规律如图1所示。根据曲线形式分为3类:衰减型、破坏型、临界型。图1 －a中曲线1、2、3、4、5 为衰减型曲线，其特点是:加载初期，应变增加较快。随加载次数增加。由于相对较小的动应力水平作用，试样逐渐压密，应变增量逐渐减小;当加载到一定次数后试样只产生弹性应变，塑性累积应变趋于稳定。破坏曲线如图1—a中曲线9、10、11、12。特点是:试样的塑性累积应变随加载次数非线性增加，一定的加载次数后，由于重复加载导致试样的结构破坏，试样强度降低，变形增量迅速增加，直到破坏。破坏型曲线近似符合Monismith公式。介于衰减型与破坏型之间的曲线为临界型(图1—a中曲线6、7、8)，其特点是:应变有时变化较大，有时变化较小，处于波动状态，表明土体处于稳定与破坏的临界状态，是区分变形稳定与彼坏的界限。这类曲线所对应的动应力定义为“临界动应力”，它是衰减型和破坏型的动应力分界点，也可以作为土体动强度指标。数值模拟参数取值如下:弹性模量10 MPa，泊松比0.27，容重为19 kN/m3，土体平均强度指标:c=33 kPa，φ =14°。土样尺寸高度10 cm，直径5 cm，划分六面体单元1 920个，单元约为2 mm的立方体，以模拟土体最大粒径。由于主要是强调荷载的循环效应，可不考虑土体的振动效应，因此采用静力有限元计算。各单元强度参数在第1步荷载之前随机生成。为取得较好的计算结果，其强度参数的变异系数由经多次试算确定为 δφ=0.18，δc=0.47。

采用轴向应力σ1=20～75 kPa、σ3=0的计算结果见图1—b所示。为了便于对比，文献［19］实测曲线如图1—a所示。

如图1—b所示，采用单元强度随机生成的有限元模拟得到的变形与加载次数关系得到模拟曲线整体上能够较好的符合试验所得到的规律:在较小的竖向动应力作用下，土体在较少的加载次数下完成塑性变形，之后塑性变形不再增加，临界动应力约55 kPa，与实测数据较为吻合。

4.2 路基变形模拟分析

采用二维平面应变模型计算，考虑的路面材料为混凝土等水硬性材料塑性变形小，而路基可产生塑性累积变形相对较大，故对路面结构与路基之间采用接触处理。路面面层、基层为弹性材料，参数取值为:混凝土路面厚度25 cm，弹性模量28 000 MPa，基层水泥稳定碎石1 500 MPa，厚度34 cm。路基采用弹塑性本构模型，回弹模量50 MPa，粘聚力均值 90 kPa，变异系数 δc=0.61，摩擦角 27°，变异系数δφ=0.22。采用正弦半波荷载模拟汽车荷载施加在路面，车轴重取 80、100、150、180、200 和220 kN。对应半波荷载峰值车轮荷载为轴重的1/2。图2为路堤几何模型及竖向变形云图，几何模型中，路基各单元的强度粘聚力和摩擦角均值和变异系数随机生成。图3为不同车辆轴载作用下车轮所在位置下路基顶面的竖向塑性累积永久变形图。

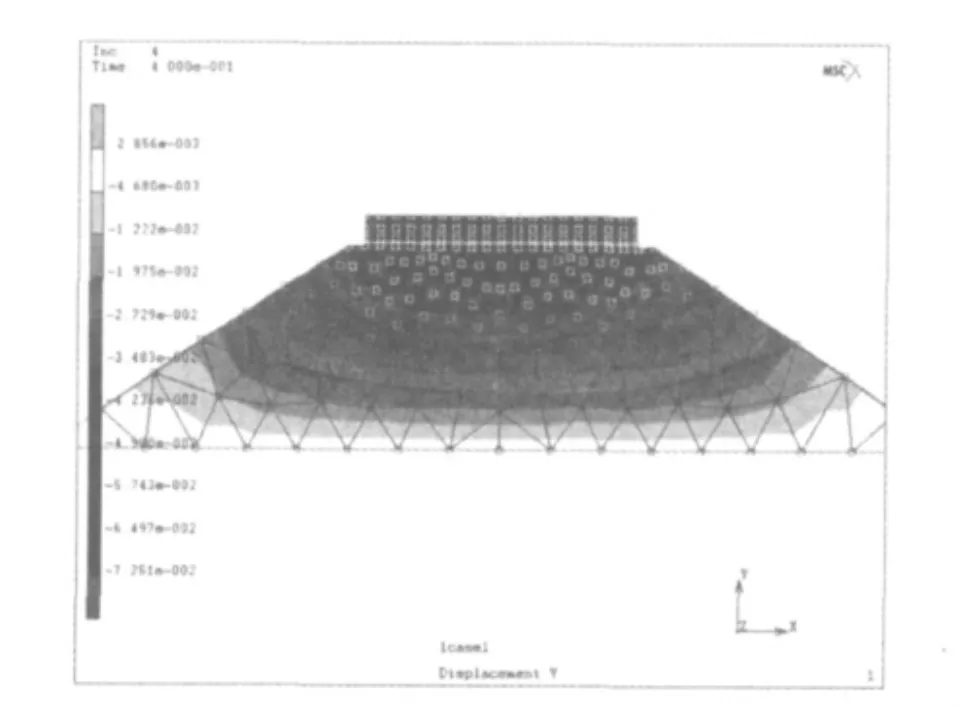
图2 路堤几何模型和竖向变形云图

从图3可以看出，路堤在不同大小的车辆荷载作用下塑性累积永久变形逐渐发展，如果汽车荷载较小，路基在车辆荷载作用下的变形可以稳定;如果荷载较大，在本例中当轴载大于150 kN，则路基在荷载作用下变形不能稳定，表现为土体移动，路基脱空，计算得到的结果符合工程实际情况。

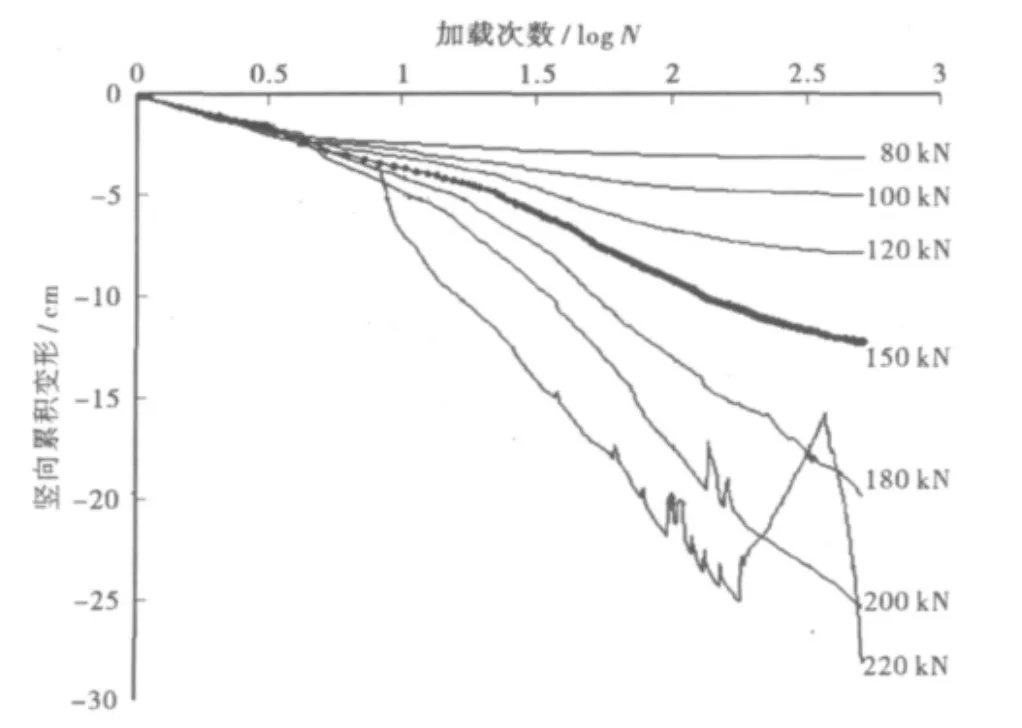
图3 路堤竖向变形与荷载次数关系

5 结论

本文在分析岩土体在重复荷载作用下永久变形产生和发展的规律以及对常用重复荷载作用下土体永久变形计算方法的基础上，采用单元强度随机生成的有限元方法对重复荷载下岩土体永久变形规律进行了数值仿真，得出以下主要结论:

1)采用单元强度随机生成的有限元方法模拟方法能够较好的表现土体永久变形的基本规律，其岩土强度变异性是导致其特殊变形性质的重要因素，算例计算结果与试验结果整体上符合较好。

2)红层软岩路堤在不同大小的车辆荷载作用下塑性累积变形逐渐发展，在较小的竖向动应力作用下，土体在较少的加载次数下完成塑性变形，之后塑性变形不再增加。

3)如果汽车荷载较小，路基在车辆荷载作用下的变形可以稳定。如果荷载较大，则沉降渐进发展而且不能稳定。在本例中当轴载大于150 kN，则路基在荷载作用下变形不能稳定，表现为土体移动，路基脱空。

［1］孙吉主，周 健.往复荷载作用下土体的广义塑性分析［J］.岩土力学，2001，22(2):126 －129.

［2］Dafalias Y F，Popov E P.A model of nonlinearly hardening materials for complex loading［J］.Acta Mechanica，1975，21(3):173－192.

［3］李进军，黄茂松，王育德.交通荷载作用下软土地基累积塑性变形分析［J］.中国公路学报，2006，19(1):1 －5.

［4］Dafalias Y F.Bounding surface plasticity I:Mathematical foundation and hypoplasticity［J］.Journal of Enginering Mechanics，ASCE，1986，112(9):966 －987.

［5］Barksdale.Repeated loading text evaluation of base coursematerials［R］.GHD Research Project No.7002，Georgia Institute of Technology，1972.

［6］Monismith，C.L.et al.Permanent deformation characteristics of subgrade soils due to repeated loading［R］.Transportation Research Record537，1975.

［7］Majidzadeh K.，Bayomy F.，and Khedr S..Rutting Evaluation of Subgrade Soils in Ohio［R］.Transportation Research Record 671，Transportation Research Board，Washington D.C.，1978.

［8］Paute J.L.，Dawson A.R.，and Galjaard P.J..Recommendation for Repeated Load Triaxial Test Equipment and Procedure for unbound Granular Materials［Z］.Proceedings of the European Symposium Euroflex1993，Lisbon，Portugal.1996.

［9］Li，D.，Selig，E.T.，Cumulative plastic deformation for fine grained subgrade soils［J］.J.Geotech.Eng.1996，122(12):1006－1013.

［10］邱延峻，孙振堂.柔性路面路基土的永久变形［J］.西南交通大学学报，2000，35(2):116 －120.

［11］Jin-Chun Chai，N.Miura.Traffic-Load-Induced Permanent Deformation of Road on Soft Subsoil［J］.J.of Geotech Eng 2002，128:907 －916.

［12］Brown，S.F.，Soil mechanics in pavement engineering［J］.Geotechnique1996，46(3):383 －426.

［13］Seed H.B.，Chan C.K.and Monismith C.L..Effect of Repeated Load on the Strength and Deformation of Compacted Clay［R］.Highway Research Record Vol.34，Highway Research Board，Washington D.C.，1955.

［14］Barksdale.Repeated loading text evaluation of base course materials［R］.GHD Research Project No.7002，Georgia Institute of Technology，1972.

［15］D.L.Heath et al.Design of conventional rail track foundation［J］.Proc.of the Institution fo Civil Engineers，1972，51:251－267.

［16］Brown S.F.，Hyde A.F.L.，Repeated load triaxial testing of silty clay［J］.Geotechnique，1975:95 －114.

［17］李献民.高速铁路加筋过渡段静动力特性数值分析及试验研究［D］.长沙:中南大学，2004.

［18］闫澍旺.往复荷载作用下重塑软土的变形特性［J］.岩土工程学报，1991，13(1):48 －53.

［19］蔡 英，曹新文.重复加载下路基填土的临界动应力和永久变形初探［J］.西南交通大学学报，1996，31(1):36 －39.

［20］程 强，寇小兵，黄绍槟，等.中国红层的分布及地质环境特征［J］.工程地质学报，2004，12(1):34－40.