用Excel 2000求解双组分精馏过程的设计型与操作型问题

金士威 唐正姣 孙炜 欧阳贻德

(武汉工程大学化工与制药学院 湖北武汉 430073)

精馏过程的计算通常涉及2种类型：一类是设计型，其任务是根据规定的分离要求，选择精馏的操作条件，计算所需的理论塔板数；另一类是操作型，其任务是在设备(精馏段塔板数及全塔理论板数)已定的条件下，由指定的操作条件预计精馏操作的结果。这2类计算均为精馏单元操作原理及其规律的具体应用，是学生必须掌握的重要知识点，也是化工原理课程液体精馏一章的教学重点。以上2类计算均需进行逐板计算或图解绘梯级，尤其是操作型计算，需多次逐板计算或绘梯级方能得解，计算强度较大。笔者在多年的教学过程中发现，多数学生对设计型计算尚存耐心，却畏惧操作型计算，不希望老师布置操作型问题的作业。

孙健哲[1]结合正、反分段函数插值法和离散点下的数值积分，进行间歇蒸馏的设计型和操作型计算，并开发了相应的计算机软件；荆涛等[2]以同样的方法对间歇蒸馏的操作型问题进行逐板计算，编写了计算机程序；潘文群等[3]运用Visual Basic编制出精馏操作型计算软件。焦勇等[4]介绍了应用PRO-Ⅱ精馏多级计算程序进行间歇精馏的拟稳态和严格模拟计算；张治山等[5]介绍了流程模拟软件Aspen Plus的一般使用方法及其在理想二元溶液板式精馏塔操作型问题中的应用。Matlab语言是一种广泛应用于工程计算和数值分析领域的新型高级语言，拥有强大的运算和图形处理功能，笔者曾应用Matlab语言估算二元系的UNIQUAC模型参数[6]及求解精馏过程中的操作型计算[7]；苏学军等[8]用Matlab语言开发了双组分精馏设计型计算程序。上述计算要么需用算法语言编程，程序冗长，学生掌握有一定困难；要么需要购买模拟软件，而国内多数高校没有购买。

Excel是Microsoft Office系列办公软件之一，拥有功能强大、使用方便的表格式数据综合管理和分析系统，能提供丰富的函数，可方便地绘出各种专业图表，可以说是最易学习与使用的中文电子表格应用软件[9-10]。笔者在教学中，对用Excel软件解决精馏过程的计算问题进行了探索，曾介绍过用Excel 2000处理精馏塔全塔效率测定实验数据的方法[11]。下面介绍用Excel 2000求解双组分精馏过程的设计型与操作型计算的方法。

1 相关知识简介

用Excel求解精馏单元操作的设计型与操作型问题，主要有3个难点：① 线性代数方程组的求解；② 根据条件选值；③ 单变量非线性方程的求解。前2点可利用Excel 2000提供的函数来实现，第3点可利用Excel 2000附带的单变量求解工具完成。

1.1 解线性代数方程组

已知线性代数方程组：AX=b。根据线性代数知识，其解为：X=A-1·b。因此，要获得线性代数方程组的解须对矩阵求逆和进行矩阵相乘操作。Excel提供了专门的矩阵求逆函数minverse和矩阵相乘函数mmult。二者的使用方法为:

① minverse函数

语法：minverse(array)

功能：返回数组array所代表的矩阵的逆。

② mmult函数

语法：mmult(array1,array2)

功能：返回数组array1与array2的乘积，结果矩阵的行数与array1相等，列数与array2相等。

1.2 条件选择

Excel提供了专门用于对数值和公式进行条件检测的IF函数，其使用方法为：

语法：IF(logical_test,value_if_true,value_if_false)

功能：logical_test表示计算结果为TRUE或FALSE的任意值或表达式。value_if_true是logical_test为TRUE时的返回值，value_if_false是logical_test为FALSE时的返回值。该函数最多支持7层嵌套。

1.3 解非线性方程

Excel提供了单变量求解工具，只要使用者输入目标函数所在单元格地址、未知变量所在单元格地址及目标函数值就可以得解，不需要编程，而且使用方便，简单易学，详见计算示例。

2 双组分精馏过程的设计型计算

算例1[12]：加料热状态对所需理论板数的影响。

欲在常压下用连续精馏塔分离苯-甲苯混合液。原料流量qn,F=100kmol/h，组成xF=0.40(苯的物质的量分数，下同)。要求馏出液流量qn,D=40kmol/h，馏出液产品组成xD=0.9，釜液产品组成xW=0.0667。操作时所用回流比R=1.875，泡点回流，塔顶为全凝器。求采用冷液进料(q=1.396)与气液混合物加料(q=3/4)时所需的最少理论板数。已知：常压下苯-甲苯混合物可视为理想物系，相对挥发度α=2.47。

解：相平衡方程为：

(1)

精馏段操作线方程为：

(2)

提馏段操作线方程为：

(3)

q=1.396时，式(3)化为：

yn+1=1.396xn-0.0264

(3a)

q=3/4时，式(3)化为：

yn+1=1.667xn-0.0444

(3b)

式(1)～式(3)中，x、y分别指液相与气相中轻组分苯的物质的量分数，下标n(或(n+1))为塔板序号，塔板自塔顶开始计数。

令精馏段与提馏段操作线方程的交点坐标为(xq，yq)，自塔顶开始逐板计算求取理论板数的计算思路见图1。显然，当完成分离任务所需的塔板数目较多时，手算过程很繁琐。

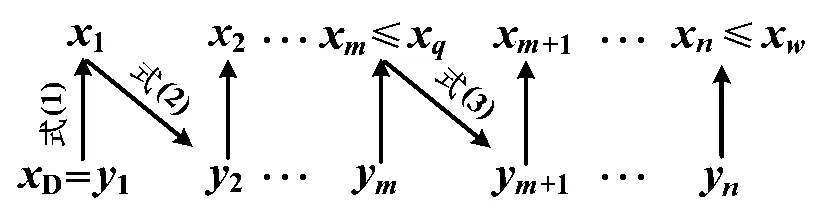
图1 逐板计算法求理论塔板数的计算思路

若用Excel软件来完成计算，则过程相对轻松。以冷液进料(q=1.396)为例，具体做法为：

① 新建Excel文档，创建“设计型”工作表。

② 先在单元格区域G3:J6，L5:L6中输入如图2所示内容；再选中单元格区域K5:K6，输入“=mmult(minverse(H5:I6),J5:J6)”；然后同时按下Ctrl+Shift+Enter组合键，将公式以数组的形式输入，则在单元格区域K5:K6立即显示得到的结果(图3)，即交点坐标为xq=0.4562，yq=0.6104。

图2 操作线方程

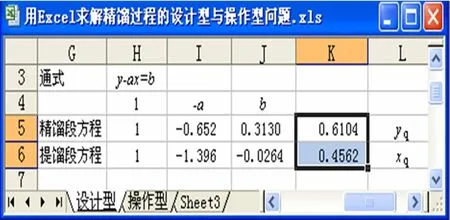
图3 两条操作线方程的解

③ 在单元格区域A1:E5中输入图4所示内容。

④ 在单元格C6中输入“=B4”即y1=xD。

⑤ 在单元格B6中输入“=C6/(2.47-1.47*C6)”，并将单元格B6的公式复制至单元格区域B7:B14，即按式(1)由气相组成yn求液相组成xn。

⑥ 在单元格D7中输入“=0.652*B6+0.313”，并将单元格D7的公式复制至单元格区域D8:D14，即根据式(2)由xn求yn+1；在单元格E7中输入“=1.396*B6-0.0264”，并将单元格E7的公式复制至单元格区域E8:E14，即根据式(3a)由xn求yn+1；在单元格C7中输入“=IF(B6>$D$4,D7,E7)”，并将单元格C7的公式复制至单元格区域C8:C14，即根据塔板处于精馏段还是提馏段选择yn+1值。

完成步骤③～⑥后得到计算结果(图4)。可见冷液进料(q=1.396)时至少需9块理论塔板，加料于第4板(x4<0.4562)。

欲求气液混合物加料(q=3/4)时所需的最少理论塔板数，只需将单元格D4的值改为0.3521，将E7的公式改为“=1.667*B6-0.0444”，就可求得结果(图5)。可见，气液混合物加料(q=3/4)时至少需12块理论塔板，加料于第6板(x6<0.3521)。上述计算结果与文献[12]一致。

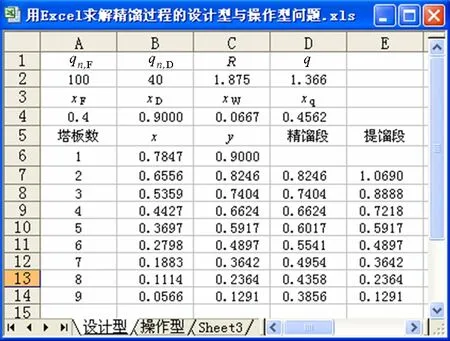
图4 算例1计算结果(q=1.396)

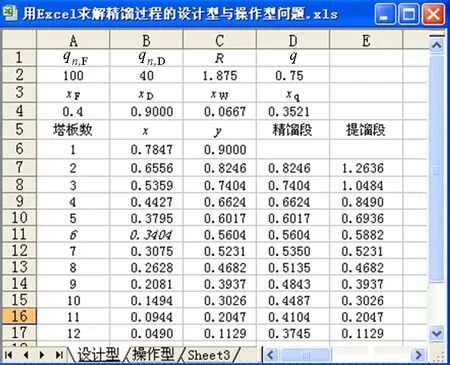
图5 算例1计算结果(q=3/4)

3 双组分精馏过程的操作型计算

算例2[13]：计算回流比变化时的产品组成及塔板组成分布。

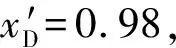
解：原工况(R=5)时，据全塔物料衡算，有：

新工况(R=8)时，据全塔物料衡算，有：

(4)

相平衡方程为：

(5)

精馏段操作线方程为：

(6)

提馏段操作线方程为：

(7)

在式(4)～式(7)中，x、y分别指液相与气相中苯的物质的量分数，下标n(或(n+1))为塔板序号，塔板自塔顶开始计数。

计算方法是以xW为试差变量，利用式(4)～式(7)求出xD及塔板上两相组成分布(图6)。若│xW-x10│≤ε(ε为收敛精度)，则表明假设的xW值正确，计算终止。

图6 塔板组成的计算思路

由上述分析可知，尽管运算过程复杂，但仅有一个未知变量xW，可用Excel提供的单变量求解工具解决。具体做法为：

① 在单元格区域A1:E1, A2:C2中输入图7所示内容。

② 在单元格D2中输入“0.085”，即按R=5时的产品组成对xW赋初值。

③ 在单元格E2中输入“=(C2-D2*(1-A2))/A2”，即按照式(4)求xD。

④ 在单元格C4中输入“=E2”，即y1=xD。

⑤ 在单元格B4中输入“=C4/(2.47-1.47*C4)”，并将单元格B4的公式复制至单元格区域B5:B13，即按照式(5)由气相组成yn求液相组成xn。

⑥ 在单元格C5中输入“=$B$2/($B$2+1)*B4+$E$2/($B$2+1)”，并将单元格C5的公式复制至单元格区域C6:C11，即对精馏段根据式(6)由xn求yn+1。

⑦ 在单元格C12中输入“=($B$2+1/$A$2)*B11/($B$2+1)-(1/$A$2-1)*$D$2/($B$2+1)”，并将单元格C12的公式复制至单元格C13，即对提馏段根据式(7)由xn求yn+1。

⑧ 在单元格D4中输入“=1e5*(B13-D2)”，即f(xW)=105(xW,计-xW,初)(采用105(xW,计-xW,初)作为目标函数是为了提高计算结果的精度)，完成以上步骤后得图7。

⑨ 选择“工具”菜单中的“单变量求解…”命令，打开“单变量求解对话框”，在目标单元格中填入“D4”，在目标值中填入“0”，在可变单元格中填入“$D$2”，单击“确定”，得“单变量求解状态对话框”；再单击“确定”，得图8。

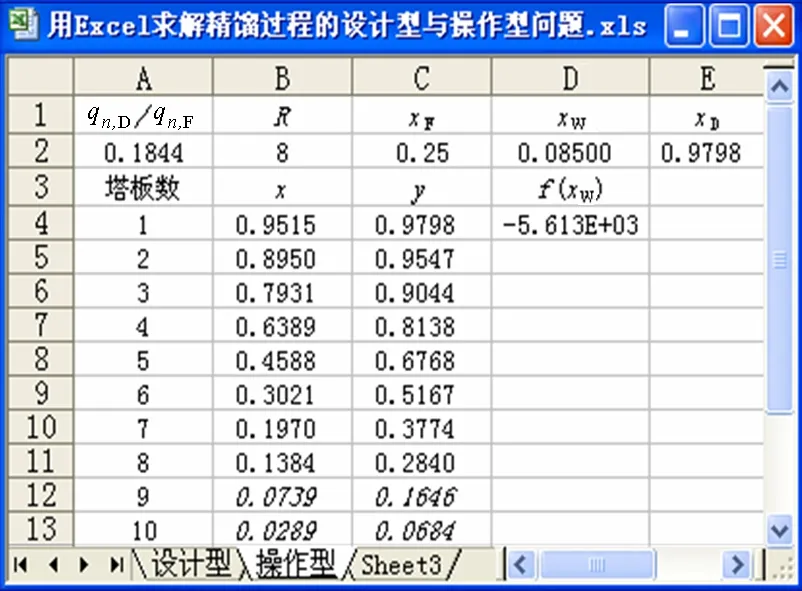
图7 算例2中间计算结果

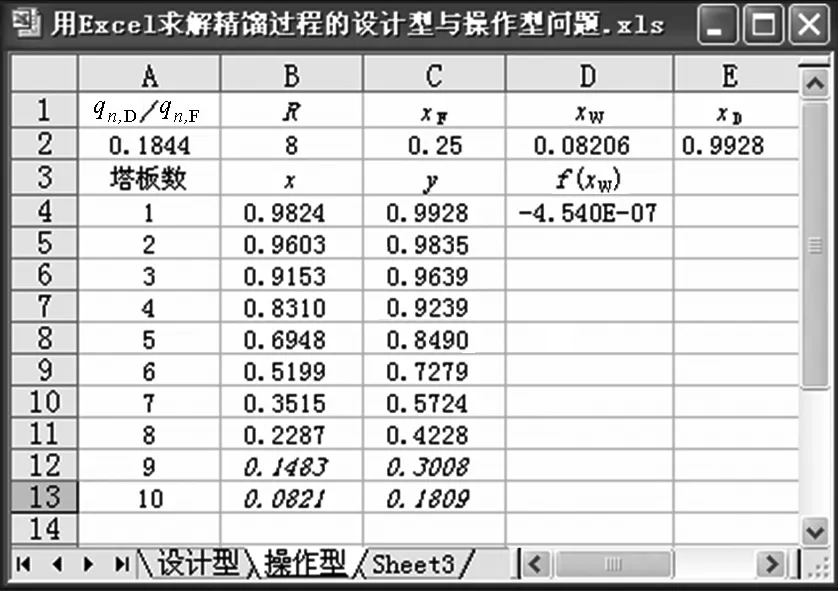
图8 算例2计算结果

新工况下xW=0.0821，xD=0.9928，各板的气液相组成详见图8。算例2表明，Excel的单变量求解工具对非线性方程f(x)=0中的函数f(x)的定义十分灵活，只要f(x)中仅包含一个未知变量即可。

若要预测其他回流比下塔顶、塔底的产品组成xD、xW及塔内各板的气液相组成，只需要修改图7中的B2单元格的值，然后操作步骤⑨，就可获得结果。表1列出了其他条件同算例2，仅改变回流比时的塔顶、塔底产品组成。结果表明，随着回流比R增加，xD升高，xW降低。

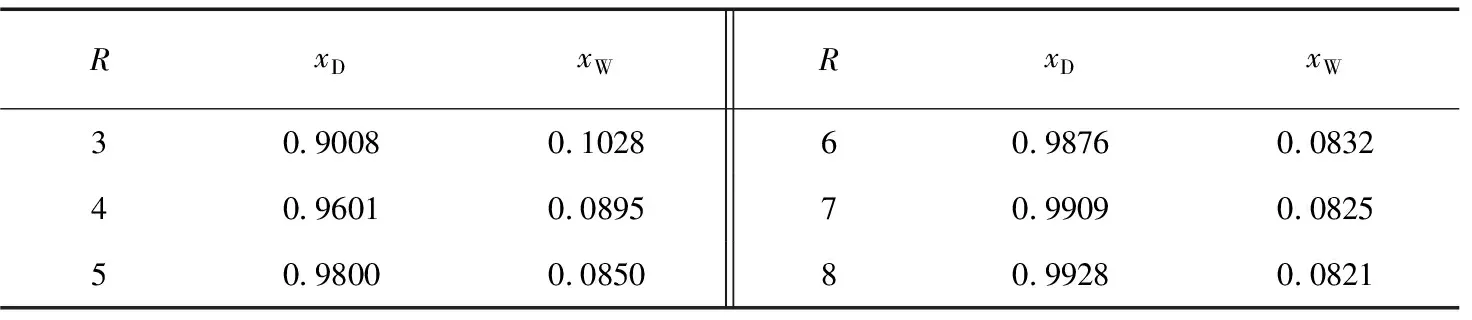
表1 不同回流比下的塔釜产品组成(其他条件同算例2)

4 教学效果评价

由以上示例可知，应用Excel求解双组分精馏过程的设计型与操作型计算，关键在于理清解决问题的思路和掌握Excel相关函数(如IF函数、mmult函数、minverse函数)和工具(如单变量求解工具)的使用方法。依笔者的多年教学实践，在教师提供详细的计算示例后，学生对用Excel解决精馏过程的设计型与操作型问题表现出浓厚的兴趣，面对繁琐的计算过程，心态也会由先前的不耐烦、畏惧变成跃跃欲试。平时只要公式中一个数据发生改变就要重新计算一遍，而Excel会自动根据新的数据更新计算结果。Excel不仅可以免除繁琐的试差计算过程，节省大量的计算时间，还可以将数据直接代入到函数中，自动返回计算后的结果，使学生能迅速知道操作条件变化后的情况，用计算所得佐证自己对问题所作的定性分析，加深对精馏操作原理和一些概念的理解,将理论与实际更好地联系起来，从而大大提高学习的积极性。

[1] 孙健哲.化工设计通讯,1995,21(3):60

[2] 荆涛,李哲.化工时刊,2003,17(5):42

[3] 潘文群,孙德松.化工时刊,2000，14(5):33

[4] 焦勇,黄洁,孙宝红,等.化工设计,2005,15(5):3

[5] 张治山,高军,李敏.中国教育技术装备,2010(15):95

[6] 唐正姣,王存文,柯文语,等.化肥设计,2007,45(3):8

[7] 唐正姣,王存文,孙炜,等.大学化学,2008,23(6):37

[8] 苏学军,王建军.天津化工,2009,23(3):59

[9] 潇湘工作室.Office 2000中文版学习捷径.北京：科学出版社,1999

[10] 赵华刚,秦振,傅远.新概念Excel 2000教程.北京：北京科海集团公司,2001

[11] 唐正姣,张光旭,欧阳贻德,等.实验技术与管理,2005,22(12):69

[12] 丛德兹,丛梅,方图南.化工原理详解与应用.北京:化学工业出版社,2002

[13] 陈敏恒,丛德兹,方图南,等.化工原理(下册).第3版.北京：化学工业出版社,2006