用哲学理念来思考物理化学的基本概念和联系*

阳历 莫婉玲 梅付名

(华中科技大学化学与化工学院 湖北武汉 430074)

物理化学是一个概念和公式比较集中的学科。如果说它复杂，那只能从侧面说明还有很多逻辑和思维可以参与的空间，还有很多联系等待我们去建立。这种联系加进一点哲学思考，会有意想不到的清晰效果。

1 范畴问题——绝对与相对

1.1 基于自然规律本身的特性产生的绝对和相对

热力学是物理化学的重要内容之一。热力学有许多概念与公式，其中热力学能U和熵S是系统本身固有的特性，具有明确的物理意义，是基于自然规律的特性而提炼出来的绝对的概念，而焓H、Holmholtz自由能A及Gibbs自由能G则是在实际应用过程中由U、S、p、V、T等物理量推断产生的相对概念，这些绝对及相对的量又通过如下热力学方程关联：

H=U+pV

A=U-TS

G=H-TS

dU=TdS-pdV

dH=TdS+Vdp

dA=-SdT-pdV

dG=-SdT+Vdp

从更普遍的意义上说，标准摩尔生成焓、燃烧焓、规定熵等都基于一个规定的起点，一切过程和变化都以这个起点为参照对象，具有一定的绝对性。只有这个绝对的概念成立了，利用Hess定律，计算任意两个相对状态转化的焓变、熵变及Gibbs自由能变化才能成立。例如：

(1)

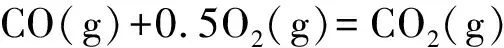
(2)

式(1)减去式(2)，得式(3)：

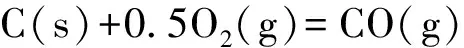
(3)

1.2 基于人为规定或总结的绝对和相对

上面讲到的都是自然过程中客观存在的绝对和相对。物理化学中还有很多人为产生的绝对和相对。通常对于一些概念的基本定义，都具有绝对性质，而基于这些概念的经验式有很多都只是相对的。

例如，电化学电解质溶液中离子的电荷、质量摩尔浓度及电导、电导率和摩尔电导率属于绝对概念，任何电解质溶液都具有这些性质。而离子强度、平均活度因子等则属于相对概念，这些绝对与相对概念之间的关系已由人们进行规定和总结。在表1中给出了其中的一些例子。

表1 物理化学中人为规定或总结的绝对和相对的典型例子

基于对绝对和相对概念的理解，可以进一步引出下面一对名词及其蕴含的原理。

2 性质问题——广度和强度

2.1 广度和强度的依赖统一

物理化学中表示系统性质时分别使用了广度性质与强度性质。前者如U、H、G等，表示与系统中物质的量相关；后者如T、p等，表示与物质的量无关；但二者又是紧密相关的。对于气体，一般是以状态方程的形式使二者依赖统一，如理想气体的状态方程，pV=nRT。对于封闭系统，可用热力学方程将广度性质与强度性质关联起来，如dU=TdS-pdV，当组成一定的系统，可用数学上更普遍的表达式如U=f(T,p)或U=f(T,V)表示二者的关联。

2.2 广度和强度的对立转化

广度性质和强度性质在某些条件下可以转化。如广度性质的物质的量就变为强度性质，广度性质的偏物质的量也是强度性质。可以看出，所谓强度性质，即是排除了物质数量干扰的量度标准，而广度性质是多起点的强度性质的总和。

2.3 广度和强度的严格区分

对于一个化学反应过程，广度性质往往起统筹的作用，强度性质往往起限制的作用。但如果是对于能量传递过程，广度性质就要和强度性质分离开来考虑。

(4)

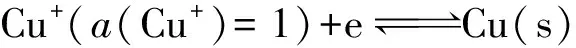
(5)

(6)

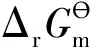
3 等效问题——真实与近似

3.1 等效的实现

这里将以电化学里一个重要的定义来解释等效的实现过程。

电解质的活度、平均离子活度及离子活度之间有如下的定义关系：

这里的离子平均活度a±定义的合理性可以这样理解，平均就是将溶液中所有离子视为无差别的质点，并将其性质平均化。这可以作为等效原理成立的基础。

等效原理的另一个作用对象不是溶液中的质点，而是化学反应，也就是以化学反应为单位进行等效。基于Arrhenius经验式，对于非基元反应，k=Aexp(-Ea/RT)中的表观活化能、表观指前因子、表观速率系数等都是等效的概念，这可以从以下关系中看出。对于某一基元反应，有k1=A1exp(-Ea1/RT)；对于另一基元反应，有k2=A2exp(-Ea2/RT)。如果表观速率系数为k=Aexp(-Ea/RT)，那么就可以根据表观速率系数k与基元反应速率系数k1、k2的关系，求出A与A1、A2以及E与E1、E2的关系。

3.2 近似是一种以多胜少的掩盖

以盐桥为例，它的作用是消除液接电势。液接电势是由于不同离子在界面的浓度和迁移速率不同，造成界面处溶液浓度改变而产生的不可逆电势。为什么这种不可逆电势会消除呢？因为盐桥里的离子承担了主要的运输任务，其他离子的作用被省略了，于是就得到了一种近似。

类似的还有Donnan平衡的消除过程。当加入的电解质浓度远大于大分子溶液的浓度时，渗透压可以用非电离大分子溶液的van′t Hoff渗透压公式进行计算。

3.3 为什么等效是正确的？

这种等效为什么是可行的呢？所有本质上的差别到哪里去了呢？从哲学观点可以这样理解：具体事物或者事物的某个具体过程相当于一个选择透过性膜，将物质属性中与研究对象没有关系的方面都过滤掉了，剩下的是等效结果。如真实气体与理想气体，当p→0时，分子间距离很远，分子间作用力很小，可以忽略；分子自由活动空间远远大于分子本身体积，以至于分子本身的体积可以忽略；此时的真实气体行为与理想气体等效。对于如何认识客观世界，哲学家康德说：“没有染指人的观念的所谓的客观世界与我们的认识没有关系，我们只能认识我们的世界。”

基于以上观点，我们可以重新看待“近似”。近似不再仅仅是对真实的一种逼近或者割舍，而在某种程度上就是真实本身。

所以可以说，等效过程在执行中是可行的，在性能上是无损的。

4 结语

基于以上3方面讨论，可以得出一个有趣的结论：世界在本质上是等效的。进一步抽象一下，所有的自发现象(无论是自然科学的还是社会科学的)都可以等效为“从不稳态到稳态的自发过程”；反过来，所有的非自发现象，也都可以等效为“从稳态到不稳态的非自发过程”。

最后我们要运用上面讨论的3个原理，继续解释新的未知。比如：Clausius-Clapeyron方程为什么和van′t Hoff等温方程非常相似？可以解释是化学势的概念把它们在本质上统一起来。但是化学势的本质又是什么呢？可以解释为“从不稳态到稳态的自发趋势的大小”。具体分析一下，这个定义里包含了绝对与相对、强度与广度以及近似与真实等要素。首先，“稳态”是绝对的静止的概念，“不稳态”是相对于稳态的概念；“趋势”代表着强度性质，而“大小”代表着强度的广度性质；而这个定义本身是对客观真实世界与主观理想的近似等效。

从这个意义上甚至可以说，哲学是一种最高形式的关于现实的抽象等效。