基于混沌神经网络公钥算法的RFID协议*
2012-09-25林传超魏腾雄李国刚
林传超, 魏腾雄, 李国刚②
(①国立华侨大学 信息科学与工程学院,福建 厦门 361021;②厦门大学 信息科学与技术学院,福建 厦门361005)
0 引言
射频识别技术是物联网感知层重要的组成部分和关键技术,是物联网“十二五”发展规划支持的重点。射频识别在得到广泛应用的同时[1],隐私和安全问题将成为首要问题。近年来关于RFID的协议很多,基于对称密钥体制的认证协议在计算复杂度方面具有优势,但在密钥管理和安全性方面却有不足[2-3]。而公钥加密算法RSA,要进行大素数的分解,涉及指数运算[4],影响运算速度,这对于硬件资源有限的RFID是个很大的问题。而基于神经网络混沌吸引子的公钥算法结合了神经网络和混沌系统各自的优点,一方面利用混沌复杂的非线性来提高算法的安全性,另一方面利用神经网络的并行处理来提高算法的加密速度,并且适合用FPGA来直接实现它的并行运算,不仅具有较高的加解密速度,而且安全性较强。由此基于神经网络混沌吸引子公钥算法提出一种RFID安全协议。
1 神经网络公钥算法
1.1 神经网络模型
一个有K个互联神经元的离散Hopfield神经网络,这K个神经元的状态用0或1表示,它的下一个状态 Si(t + 1 )与当前各神经元的状态 Si(t)的关系如下:
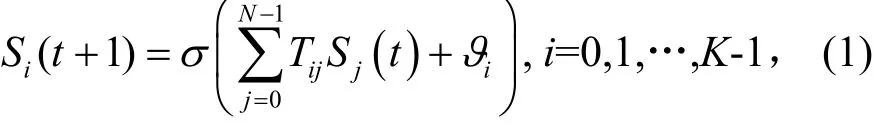
式中, Tij为神经元i与j之间的联接权值, ϑi为神经元i的阈值, σ ( x )为任一非线性函数, 不妨设为一符号函数,即:

在HNN模型中,神经元的阈值ϑi可定义为0,Tij为一对称矩阵。Hopfield已证明能量函数随系统状态的演进而单调下降[5],最终会达到一种稳定状态,即混沌吸引子[6],每个吸引子的吸引域有多个状态,且彼此之间关系没法预测;吸引子及其相应的吸引域会随着联结突触矩阵T的改变而改变。从公式Sˆ=HS和Sˆμ= H Sμ可知,原始状态S和吸引子Sμ左乘一个非奇异变换H后,变为新原始状态Sˆ和吸引子Sˆμ。
1.2 基于混沌吸引子的Diffe-Hellman公钥体制
根据Diffie-Hellman公钥密码体制的思想[7], 假定在一群用户中有两个用户 A和 B要进行保密通信,他们共同选择一个n阶奇异方阵为联结突触矩阵T0,然后再从n阶方阵可交换族中任意选取一个非奇异变换方阵 Ha和 Hb作为自己的私钥,使得 Ha和 Hb满足 Ha* Hb= Hb*Ha,A和B用户分别计算Ta=Ha* T0*Ha', T b =Hb* T0* Hb', Ha'和 H b'分别为 Ha与 Hb的转置矩阵,之后将 Ta和 Tb作为公钥公开,而将作为两者的公共密钥,这样只有用户A和用户B可以从自己的私钥和对方的公钥计算出公共密钥 T,而其他人无法从公钥 Ta和 Tb计算出私钥和公共密钥,特别当n较大时[6]。
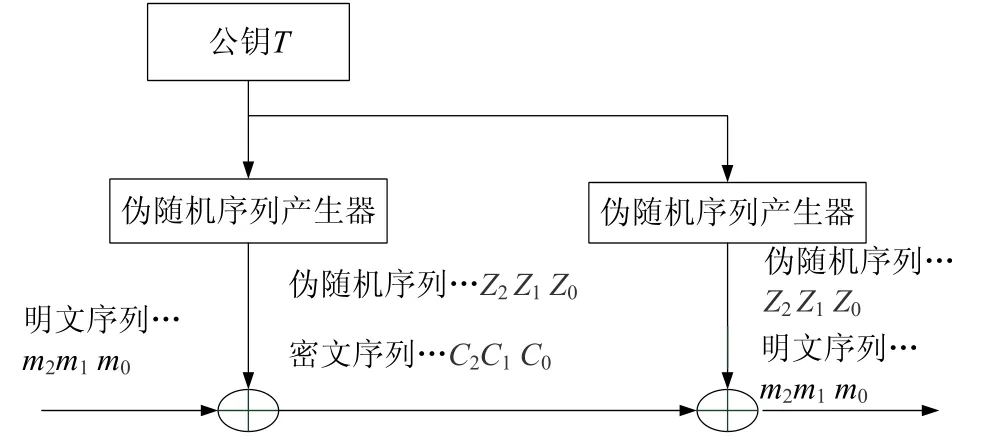
图1 基于神经网络混沌吸引子的公钥密码算法
1.3 算法的设计与实现
通过Diffie-Hellman公钥密码体制进行公共密钥T的计算,完成公钥的交换,然后通过公钥产生的流密码对信息进行对称加解密。为防止第三者的假冒攻击, 通信两方可使用数字签名和公钥证书对彼此进行身份验证,即采用带认证的Diffie-Hellman密钥交换协议[8]。此混合加密方案兼顾流密码加密效率高、速度快与公钥算法密钥管理方便、安全性高的优点,产生伪随机序列方案简单,易于硬件实现。
如图2所示,伪随机序列产生器选用若干m序列作为序列密码的驱动源,将离散Hopfield神经网络作为非线性函数部分进行选择控制输出,这样既保留了m序列的随机性,又能提高其复杂度和周期。各LFSR的的初始值可以由公共密钥T的矩阵中随机选取适当个数的元素运算后确定(例如大于等于0的数设为1,小于0的设为0),且通信双方必须一致,然后把2n个LFSR的输出值当作神经网络的输入值,在加密器中计算出新的吸引子,再依照产生的新吸引子,对2n个LFSR的输出值进行多选一操作,由此产生伪随机序列。
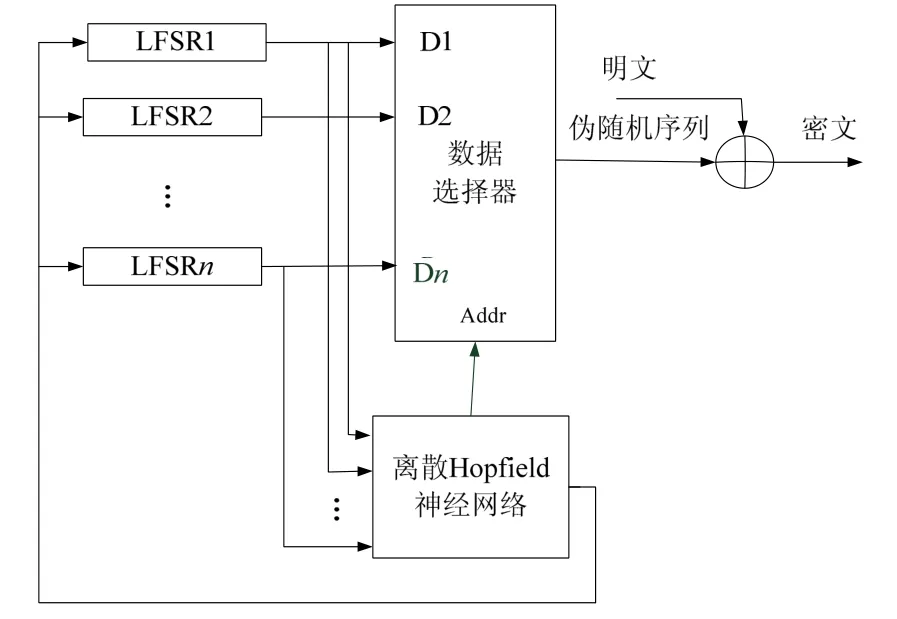
图2 伪随机序列产生器
2 RFID安全协议
2.1 工作原理
在前端对标签内的信息通过公钥进行加密,加密后的信息经过读写器传给后端服务器。后端服务器通过私钥解密传来的加密信息,通过与数据库的数据进行比较检验其合法性,进而得到标签内的信息。为了避免跟踪和重传攻击,标签每次都要生成一个随机数并进行哈希运算,运算后的数据与标签ID等信息合并后才进行公钥加密。
2.2 协议算法
基于神经网络混沌吸引子公钥算法的RFID安全认证协议过程如下:
1)读写器R产生一个随机数r,对r进行Hash运算得 I = H (r),然后发出I以查询访问标签L。
2)标签L收到I后,利用标签内的公钥 Ta、私钥 Hb,生成公共密钥 T =Hb* Ta*,再加密N = ET(I D ||M | |I ),其中ID为标签的唯一标识号,M为标签内的信息数据。同时计算P = N ⊕ I ,并将N和P返回给读写器R。
3)读写器R将从标签发来的的N,P,以及I,r发向后端数据库,数据库通过I和 H (r)是否相同来验证R的身份,若阅读器R合法,再用私钥 Ha、Tb生成公共密钥 T =Ha* Tb*,再解密N,得到ID'||M'||I =(N ),将得到的 ( I D', M') 与后端数据库中的每个(I D ,M ) 比较,并检验P是否等于N⊕I,若其中任意一个不符合,则认证失败,读写器将丢掉收到的数据。
4)在3)成功认证的基础上,读写器R接收后端数据库发来的数据M,就得到标签内的信息。
3 性能分析
3.1 安全性
该协议可以有效地抵抗重传攻击,假设攻击者获得标签和读写器之间传输的数据N,并企图下次向读写器重传该数据伪装成合法标签,但是读写器在每次查询访问标签时,都会构造新的随机数r,如果读写器在收到重传的数据N后,并将其传送到后台与数据库进行比较,结果肯定不相等,故丢弃该数据,从而有效地防止重传攻击。
此外标签每次向读写器传送的密文N = ET(I D||M | |I),I = H (r),由于每次的随机数r都不相同,故每次的N也都不同,而且跟前次的N没有关联,所以第三方没法判断两次的数据是否同源,进而避免被跟踪。
如果攻击者通过篡改数据N中的信息发动主动攻击,则篡改后的数据N在后台服务器被解密后,通过与数据库的比对,马上会被发现错误,因此通过主动攻击篡改数据N也不能成功。
3.2 加密效率与速度
由于基于神经网络混沌吸引子的公钥加密算法关键在于高阶奇异矩阵的分解[8],而RSA算法关键在于数学难题中大素数的分解,因而前者加密速度更快、更适合现代的组加密通信和现代商务加密通信的需求。
RSA算法其安全强度依赖于密钥的长度,正常必须大于1024位,并且随着安全性能的增强需要对应的密钥长度增长的也快,占用的资源(存储空间)增加,导致实现起来对硬件的要求较高,因此还不能适应现在的RFID等计算能力较低的终端产品上。
1.3 给出的公钥算法改进了文献[9]的算法,取消了过度搜索,同时取消了编码过程,不存在密文膨胀,计算1次混沌吸引子就可以加密1 bit信息,加密速度比文献[9]平均快2n/n倍。本协议算法已经在VC6.0平台上编程实现,并且在FPGA硬件上通过VHDL语言实现,最高运行频率达到50 MHz[10]。
4 结语
随着物联网的兴起,作为感知层重要应用的RFID射频技术安全问题日益受到关注。分析了不同中RFID协议的优缺点[11-12],提出一种基于神经网络混沌吸引子公钥算法的RFID安全协议,并对其可行性和性能进行分析,结果表明该协议具有较高的安全性和较快的加解密速度,在保证效率的同时能较好的保护标签数据的隐私,适用于RFID系统。
[1] 叶里莎. RFID技术的应用[J].通信技术, 2007,40(12):267-271.
[2] 刘庆华,霍腾飞,邓依群,等. 基于Hash函数的随机RFID认证协议[J].通信技术, 2009,42(08):59-61.
[3] KIM H W, LIM S Y, LEE H J. Symmetric Encryption in RFID Authentication Protocol for Strong Location Privacy and Forward-Security[C]//Proc.of Conference on Hybrid Information Technology. Korea:[s.n.],2006:718-723.
[4] 靳丽君. 非对称加密体制中RSA算法的研究[J]. 电子设计工程, 2011(11):29-30.
[5] JOHN J H. Neurons, Dynamics and Computation[J].Physics Today, 1994,47(02):40-46.
[6] GUO D, CHENG L M, CHENG L L. A New Symmetric Probabilistic Encryption Scheme Based on Chaotic Attractors of Neural Networks[J]. Applied Intelligence,1999, 10(01): 71-84.
[7] DIFFIE W, HELLMAN M. New Directions in Cryptography[J]. IEEE Transactions on Information Theory, 1976,22(06): 644-654.
[8] EMMANUEL B, OLIVIER C, DAVID P,et al. Provably Authenticated Group Diffie-Hellman Key Eexchange[C]// Proceedings of the ACM Conference on Computer and Communications Security.Philadelphia: ACM Press,2001:255-264.
[9] 刘年生,郭东辉. 一种新的基于神经网络混沌吸引子的公钥密码算法[J]. 集美大学学报:自然科学版,2005,10(02):125-133.
[10] 张阳. 神经网络混沌加密算法的研究与FPGA设计[D].福建:华侨大学, 2011.
[11] 孔令荣,樊矾.一种RFID标签信息安全传输协议[J].信息安全与通信保密,2011(07):90-91,94.
[12] 高正中,盛惠兴,宋依青.射频识别系统中安全认证协议的研究[J].信息安全与通信保密,2010(08):41-43.
