利用随钻正交偶极子声波测井评价地层各向异性的数值研究

王瑞甲，乔文孝＊，鞠晓东

1 中国石油大学油气资源与探测国家重点实验室，北京 102249

2 北京市地球探测与信息技术重点实验室，北京 102249

1 引 言

随钻声波测井在节省井架占用时间、利用测得的声波速度模型与地震勘探数据相结合实时确定地层界面的位置、估算地层孔隙压力等方面有着电缆测井无法比拟的优势[1］.关于随钻声波测井的研究，国内外已做了大量的工作.Minear和Legget成功实现了地层随钻纵波测量[2-3］；Tang等认为采用四极子声源进行随钻横波测量有着偶极子声波测井无法比拟的优势[4］；Sinha等也研究了随钻测井模型下各向同性地层井孔内导波的基本响应特征[5］.目前，随钻声波测井仪已基本实现了地层纵、横波测量的功能，下一步所面临的挑战是对地层的声学各向异性进行测量.

各向异性测量主要包括快横波面方位的确定和横波各向异性值的测量两个方面.尽管四极子声源在随钻地层横波测量方面取得了成功，但是限于其方位特性，很难利用四极子声源实现随钻地层各向异性测量.虽然部分学者已经在此方面开展了一些工作[6］，但是至今未见成功利用四极子声源实现地层各向异性测量的报道.采用正交偶极子声波测井方式评价地层各向异性的方法已经在电缆测井中得到了广泛的应用[7］.因为随钻四极子声波测井仪换能器的安装位置同正交偶极子声波测井仪器相同，且其接收站兼具备正交偶极子接收功能，通过合理的电路设计，可以较为方便地实现随钻正交偶极子声波测井，所以采用正交偶极子声源进行地层各向异性评价的方法为随钻地层各向异性测量的首选方式.研究各向异性地层随钻正交偶极子声波测井的响应特征，对偶极子声源在含钻铤各向异性地层井孔内激发的声场进行分析，可以帮助理解在随钻条件下各向异性地层井孔内沿井轴方向传播的弯曲波的特征，为新一代随钻声波各向异性测量仪器的设计及测量方案的设计提供理论指导.

有关各向异性地层井孔声场的研究，国内外已经做了大量的工作.Cheng采用三维直角坐标系有限差分方法模拟了正交各向异性地层包围的井孔内多极子声源激发的声场[8］.Schmitt研究了介质对称轴同井轴平行情况下，多极子声源激发的模式波的频散曲线及衰减曲线，并分析了各地层参数对于井孔内导波的影响[9］.Sinha采用三维柱坐标系有限差分方法模拟研究了典型的硬地层和软地层条件下，TI地层斜井情况下多极子声源激发的声场以及仪器的存在对于井内模式波频散特征的影响，他认为，各向异性地层中，弯曲波在低频下的传播速度为对应地层横波的相速度[10］.王秀明采用三维直角坐标系有限差分方法计算了TI地层斜井中的单极子声源和偶极子声源激发的声场，他的模拟结果表明声波测井所测得的弯曲波的速度同各向异性地层体波的群速度一致[11］.张碧星分别采用实轴积分和摄动积分的方法研究了TI地层中模式波的频散特性和激发强度[11］.陈雪莲和王瑞甲采用实轴积分法模拟了径向分层TI孔隙介质井孔内多极子声源激发的声场，并着重研究了渗透率对模式波衰减和幅度的影响以及井孔模式波的探测深度问题[12-13］.He和Hu等从理论上推导了井孔弯曲波的低频极限速度公式，并采用三维柱坐标系有限差分算法模拟了TI介质斜井中的弯曲波，他们的研究结果表明，大多数情况下，快、慢弯曲波的慢度近似等于沿井轴方向传播的地层快、慢横波的慢度[14-15］.闫守国和宋若龙等也模拟了横向各向同性斜井中偶极子声源激发的声场，并提出了采用守恒积分的方法解决柱坐标系波动方程在井轴上出现的奇异点的问题[16］.上述的研究均为电缆测井情况下各向异性地层声波测井模拟，鲜见有关在随钻条件下各向异性地层偶极子声源激发声场研究的报道.

即使在地层为各向同性的情况下，由于钻铤占据了井内的大部分空间，随钻条件下的弯曲波的频散特性、激发特征均与电缆测井不同[1，17］.在地层为各向异性的情况下，偶极子声源激发的声场将更为复杂，无法采用解析的方法进行模拟.地层介质最为广泛存在的一种各向异性介质模型为横向各向同性（TI）介质.本文采用三维有限差分方法模拟研究了横向各向同性（TI）地层随钻正交偶极子声波测井，对地层的声学各向异性在随钻正交偶极子声波测井中的响应特征进行了分析，对采用随钻正交偶极子声波测井方式进行各向异性测量的可行性进行了评价.

2 TI地层随钻声波测井声学模型

与电缆测井不同，在随钻声波测井中，钻挺占据了井孔内的大部分空间.由于钻铤的存在，井孔内沿井轴方向传播的各种模式波的性质同电缆测井不同.图1a为TI地层随钻测井声学模型示意图，S方向为TI介质的对称轴方向，它与井轴的夹角为α.如图1b所示，TI地层随钻测井声学模型可以简化为柱状径向分层声学模型，沿井径方向从内向外的介质依次为水、钢（钻铤）、水、地层，各介质的外径分别为r0、r1、r2和无穷大.井孔内充满流体.井孔外地层为无限大TI介质.钻铤位于井孔中央，钻铤中间的水眼中充满水.在实际测井中，尤其是在钻进过程中，钻铤并非完全居中，此时井中的声场将更为复杂.为了突出本文所关心的问题，本文的模型假设钻铤在井孔中完全居中.

3 数值模拟方法

3.1 波动方程的离散化

由于地层为各向异性介质，该问题不存在解析解，必须采用数值方法来模拟地层中的声传播.三维有限差分方法是模拟复杂介质中声传播问题的常用方法[6，8，10-11，15-16，18］.本文采用三维有限差分方法来模拟随钻情况下的各向异性地层井孔中的声传播.任意各向异性介质中的运动方程和本构方程分别为式（1—3）和式（4）：

图1 随钻测井声学模型示意图，包括（a）TI地层井孔随钻测井声学模型和（b）井孔横截面示意图Fig.1 Schematic of LWD acoustic model，including（a）acoustic model of borehole surrounded by TI formation in LWD conditions and（b）the cross section of the borehole

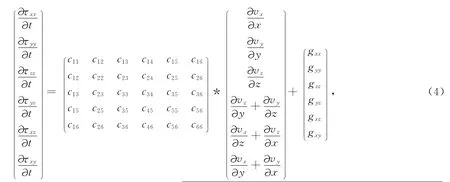
其中vx、vy、vz分别为x、y、z方向上质点振动速度分量；τxx、τyy、τzz分别为x、y、z方向上的正应力；τxy、τyz、τxz为剪切应力；ρ为介质的密度；cab（a=1～6，b=1～6）是各向异性介质的刚性系数.特别地，对于TI介质，当介质对称轴同z轴平行时，式（4）中仅c11、c12、c13、c22、c23、c33、c44、c55和c66不为零，且满足c12=c11-2c66、c23=c13、c22=c11和c44=c55，其它元素为零，这样采用c11、c13、c33、c44、c66五个参数即可描述TI介质中的波传播现象.通过Bond变换可以获得当介质对称轴同z轴呈一定夹角时介质的刚性系数矩阵[19］.对于TI介质，当介质对称轴在x-z平面内且同z轴呈一定夹角时，除上述几个参数之外，c15、c25、c35和 c46也不为零.右侧的gab（a、b=x～z）表示力变化速度的体积源，和体力源fi（i=x～z）组合使用可以模拟各种声源.

图2 交错网格1／8元胞示意图Fig.2 Schematic for 1／8cell of staggered grid

我们采用了交错网格的方式来实现差分的显式迭代过程.图2为采用的交错网格1／8元胞示意图.式（5）为速度和应力各分量在空间和时间上的位置，其中l表示网格的空间位置.正应力各分量τxx，τyy，τzz均位于整数网格节点上，切应力各分量和速度分量分别位于各自对应的半整数网格节点上.对于本文研究的TI地层与井轴斜交的情况，由于刚性系数矩阵元素c15、c25、c35和c46不为0，根据网格上各个物理量之间的位置关系，仅采用交错网格无法进行差分近似处理.如图2所示，在采用式（4）计算时，由于c15、c25、c35和c46不为零，需要网格 （lx，ly，lz+1／2）处的速度值以及网格 （lx+1／2，ly+1／2，lz+1／2）的速度值，网 格（lx+1／2，ly+1／2，lz+1／2）的速度值针对此问题，一种解决方法是采用对速度场进行插值的方法获取上述点的速度值，另外一种方法是采用辅助交错网格的方法.本文采用了对速度场进行插值的方法.

如式（6—9）所示，在计算时，首先计算该网格点上的应力值，应力值τxx的计算方法如式（6）所示，其他应力值的计算与式（6）类似，此处不做赘述.普通交错网格处的速度值仍旧按照式（1—3）进行计算，网格上 （lx，ly，lz+1／2）处的速度值网格 （lx+1／2，ly+1／2，lz+1／2）的速度值以及网格 （lx+1／2，ly，lz）的速度值可以通过对速度场进行插值的方法获得，如式（7—9）所示.据此，可以完成差分算法的显示迭代.

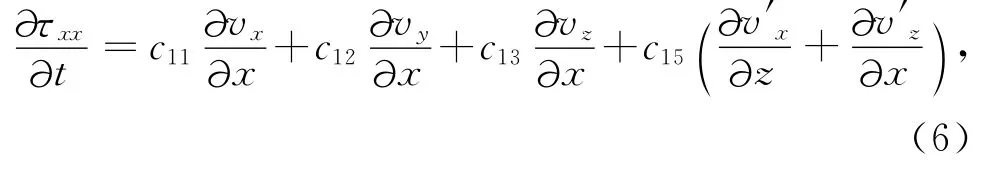
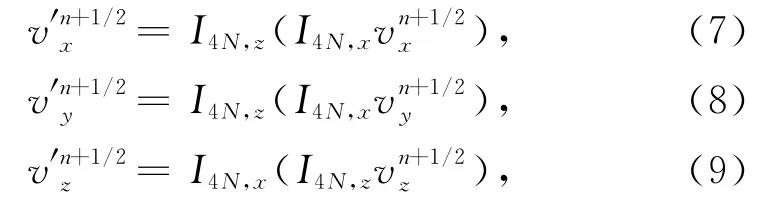
其中，式（7—9）中，I表示平移算子，其两个下标分别表述平移算子的空间阶数和平移算子的方向.N为差分算子所采用的空间阶数的一半.

采用本文的网格划分方法对式（1—4，6—9）进行离散化处理，得到显式的差分迭代格式.式（10）和式（11）分别为速度分量vx和应力分量τxx离散差分格式，其他分量及辅助交错网格各分量的迭代格式形式类似.

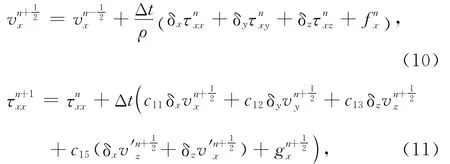
式（10～11）中，δx、δy、δz分别代表物理量在x、y、z方向的差分，Δt为计算采用的时间步长.

3.2 稳定性条件

在直角坐标系下，对于一般的各向异性介质，有限差分计算方法的稳定性条件为[11］

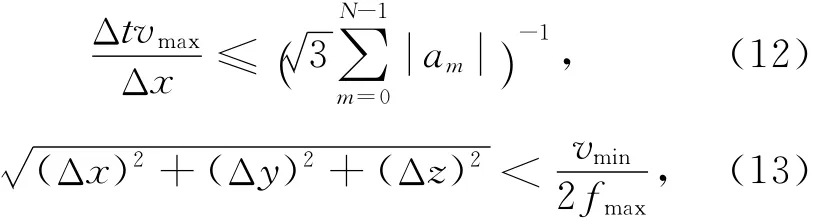
式（12～13）中，vmax和vmin代表计算模型速度的最大值和最小值，am为采用的差分系数，Δx、Δy、Δz分别代表x、y、z方向的空间步长，fmax为声源覆盖的最高频率.

3.3 声源的实现

本文采用两个紧贴钻铤外侧振动相位相反的点声源来模拟偶极子声源.点声源的加载方法为式（14）所述形式[20］：

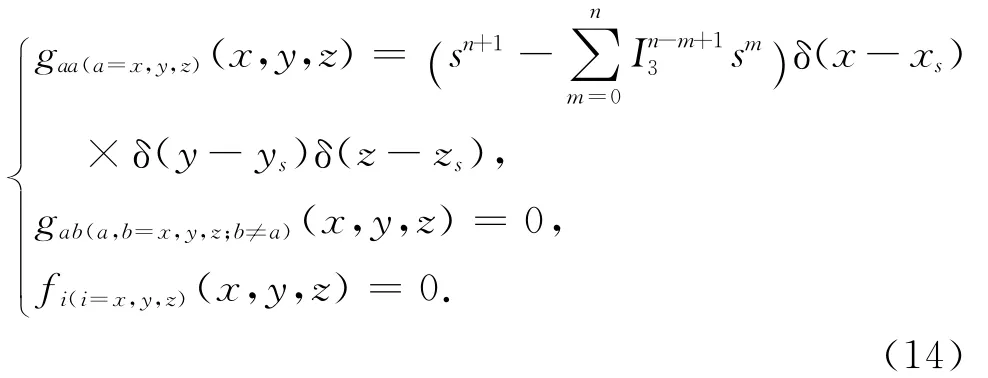
式（14）中，I3为三维直角坐标系中网格的脉冲响应，sn为第n次迭代时加载的声源值，δ为单位脉冲函数，xs、ys和zs分别为声源在x、y、z方向的坐标.声源函数采用了雷克子波函数，如式（15）所示.

3.4 边界的处理

在计算中，介质的刚性系数和密度均赋在整数节点上，对于非整数网格点的物理量，通过临近网格的物理量的平均得到.非整数网格点处的密度，通过式（16～18）所示的平均的方法获得.非整数网格点处的刚性系数通过如式（19～21）所示的计算方法获得.这样对于固液界面（钻铤-流体边界和流体-地层边界），通过式（16～21）所给出的平均的方法，边界条件自动满足.

为了模拟无限大的地层，采用了完全匹配层（PML）技术来吸收向地层内传播的波[18］.PML层厚度选为地层纵波波长的一半.

3.5 并行实现

由于模型计算量较大，采用传统的串行计算方法无法满足计算需求.我们采用了OpenMP和MPI混合编程技术，将有限差分算法在集群上实现.MPI是目前在集群上应用最为广泛的并行计算技术.OpenMP虽然仅适用于单机多核计算，但是其计算效率高，易于编程实现，且目前大部分编译器都已经支持OpenMP技术.本文通过采用OpenMP和MPI混合编程技术，简化了并行算法的复杂性，提高了程序的执行效率.如图3所示，x和z分别代表直角坐标系的x方向和z方向，m和n分别代表采用的进程数和线程数，双向箭头表示相邻进程之间的通信.通过合理的计算区域划分，将计算任务分配到每个参与计算的节点上.通过MPI技术，在每个计算节点上开辟一个进程，通过进程间的通信和协作，实现计算的并行.在一个节点上，运用OpenMP技术，开辟多个线程，利用多核协同工作，加快计算的速度.

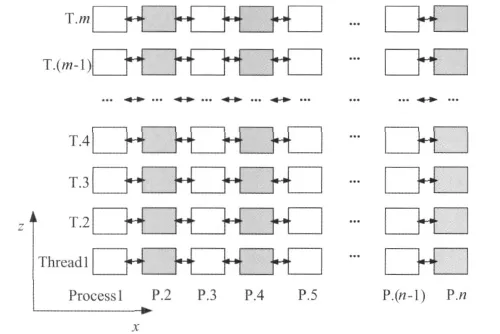
图3 并行计算方案Fig.3 Parallel implementation of the algorithm

对于240×240×300个网格，20000个时间步长的数值模型，采用5个CPU核心数为12的节点进行计算，每个节点开辟的线程数目为11，采用双精度进行计算时完成计算所需的时间大约为20h.

4 数值模拟结果及分析

4.1 数值模型参数

图4为数值计算模型示意图，包括（a）模型主计算区域和（b）井孔横截面示意图.模型主计算区域的尺寸为1m×1m×4.8m，x、y、z方向的空间采样间隔分别为0.0075m、0.0075m和0.0125m.井孔位于模型中央，井轴与z轴平行.介质对称轴S位于x-z平面内，介质对称轴与井轴夹角为α.特别地，当α=0°时，井轴与介质对称轴平行，相当于竖直井井孔沿对称轴穿过VTI地层，当α=90°时，井轴与介质对称轴垂直，相当于竖直井井孔沿垂直于介质对称轴的方向穿过HTI地层.数值模拟时采用的地层参数为实验室内测量的各向异性介质的参数，该介质在TI对称轴与z轴平行情况下的刚性参数如表1所示.井孔内流体及钻铤参数见表2，钻铤内径、外径及井眼直径分别为0.054m、0.180m和0.240m.声源加载在距离底界面0.8m处，采用在钻铤外径处加载两个震动相位相反的点声源的方法来模拟偶极子声源.偶极子接收器同样放置于钻铤外径处，接收器源距为2.0～3.5m，间距为0.15m.由于本文重点研究的对象为地层弯曲波，不涉及隔声及钻铤波问题的研究，为压制钻铤波，在发射器到源距最小的接收器之间将钻铤截断.

表1 地层参数Table1 Formation parameters

表2 钻铤及钻铤内外流体的参数Table 2 Parameters of the collar and the fluid in and out of the collar

图4b为x-y平面内井孔横截面示意图.为描述方便，定义地层横向同性面和井轴垂直面之交线与偶极子声源偏振方向的夹角为β，发射探头和接收探头所对应的夹角分别为βT和βR.特别地，对于本文α=90°的井孔模型，β为偶极子声源偏振方向同快横波面的夹角.当βT=βR时，接收器与发射器偏振方向相同，测得波形为同向分量波形；当βR=βT+90°时，接收器与发射器偏振方向相差90°，测得波形为正交分量波形.特别地，当βT=0°时，声源的偏振方向与地层中传播的SH波偏振方向一致；当βT=90°时，声源的偏振方向与地层中传播的准SV波偏振方向一致.

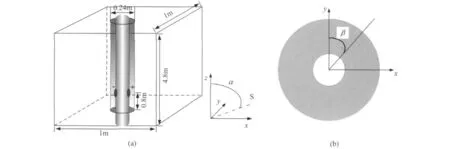
图4 数值模拟采用的模型示意图（a）及x-y截面示意图（b）Fig.4 Schematic diagram of numerical simulation model（a）and diagram of x-ycross section（b）

本文首先模拟了α=90°，βT=0°、21.25°、45°、68.75°和90°情况下正交偶极子声波测井，借以研究在井轴与TI介质对称轴垂直的情况下，随钻正交偶极子声波测井对地层各向异性的评价能力，然后计算了α=0°、15°、30°、45°、60°、75°、90°，βT=0°、90°情况下偶极子声源激发的声场，研究不同井斜情况下的随钻正交偶极子声波测井的响应特征.

4.2 正交偶极子波形

图5 α=90°时，βT=0°、90°偶极子在井孔中激励的偶极子波形，源距为2.0～3.5mFig.5 Dipole waveforms excited in the borehole by dipole source of source-receiver space 2.0～3.5m withα=90°，βT=0°、90°

数值模拟了α=90°，βT=0°、90°情况下偶极子声源在井孔中激发的模式波.图5为数值模拟结果，其中实线为声源和接收器的方向βT，βR=0°时测得的偶极子波形，虚线为声源和接收器的方向βT，βR=90°时测得的偶极子波形.可以看到，βT=0°时偶极子声源激励的弯曲波的传播速度大于βT=90°时偶极子激励的弯曲波的传播速度，同对应的地层体波SH波和SV波（在α=90°时，纵波和SV波不耦合）的速度相一致.这表明，在钻铤存在的情况下，不同方向的偶极子声源激发的弯曲波速度的差异同地层横波速度的各向异性有关.

数值模拟了α=90°，βT=0°、21.25°、45°和68.75°和90°情况下，偶极子声源在含钻铤井孔内激发的声场.图6为不同角度下偶极子声源在井孔中激发的同向分量波形（a）和正交分量波形（b）.从图6中可见，当βT=0°或者90°时，几乎接收不到正交分量波形信号，当βT=21.25°、45°、68.75°时，正交分量能量较强，且当βT=45°时正交分量能量最强；而同向分量波形能量在βT=0°或者90°时幅度较强，在βT=45°时幅度相对较弱.同向分量和正交分量的能量变化表明，在βT=0°或者90°时，弯曲波未发生分裂现象；βT=21.25°、45°、68.75°时，弯曲波发生了分裂现象.图6的模拟结果证实了，对于井轴同介质对称轴垂直的TI地层井孔，同电缆测井一致，在随钻条件下，弯曲波分裂现象仍然存在.

图6 α=90°，βT=0°、21.25°、45°、68.75°和90°时，模拟得到的（a）同向分量波形和（b）正交分量信号，源距为2mFig.6 Simulated inline component waveforms（a）and cross-line component waveforms（b）of source-receiver space 2mwithα=90°，βT=0°、21.25°、45°、68.75°and 90°

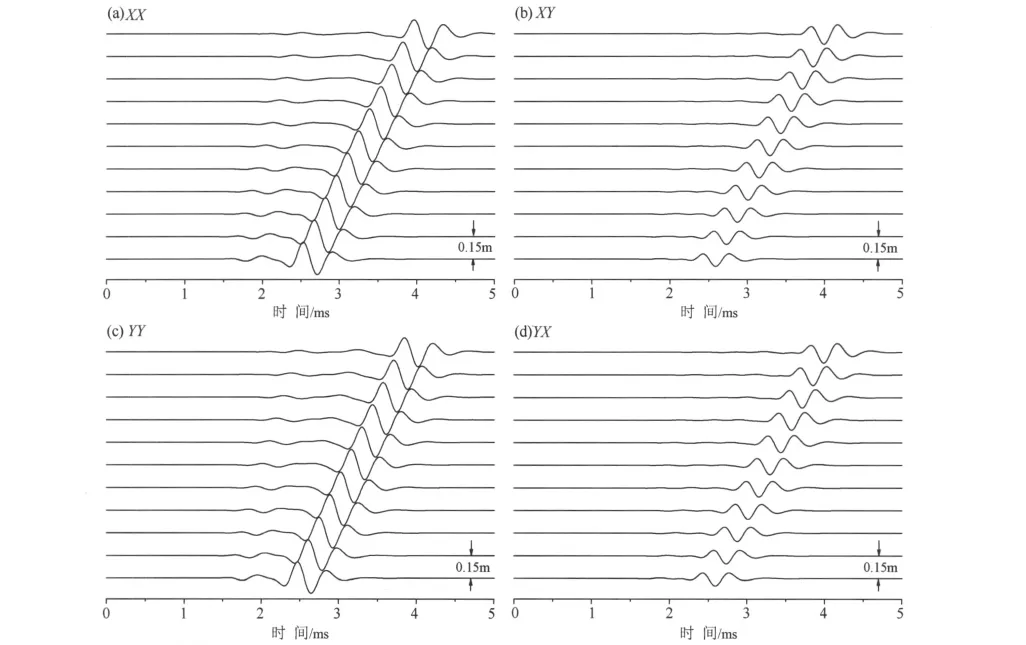
图7 α=90°，βT=68.75°时，数值模拟得到的四分量偶极子波形，包括同向分量波形（a）XX 和（c）YY，以及正交分量波形（b）XY和（d）YX，源距为2～3.5mFig.7 Simulated four-component dipole waveforms including incline component waveforms（a）XXand（c）YY，and cross-line component waveforms（b）XYand（d）YXof source-receiver space 2～3.5mwithα=90°，βT=68.75°

假设正交偶极子声源的两个正交的方向分别标记为X和Y.模拟了X方向同快横波面的夹角分别为βT=0°、21.25°、45°、68.75°、90°几种情况下正交偶极子声源在含钻铤井孔内激发的四分量偶极子波形.图7为βT=68.75°情况下模拟的四分量偶极子波形，包括同向分量波形（a）（c）和正交分量波形（b）（d）.对于各向同性地层，由于各方向地层声学参数均相同，不会接收到正交分量信号；对于各向异性地层，当声源偏振方向同介质对称轴呈一定夹角时，由于各向异性地层的耦合作用，会接收到正交分量.从图7中可以看到，正交分量信号XY和YX 均有较强的幅度，说明发生了弯曲波分裂现象.综上所述，在含钻铤TI地层井孔中，βT=0°、90°时偶极子声源激励的弯曲波未发生分裂现象，分别以较快、较慢的速度沿井轴传播；当声源偏振方向同介质对称轴呈一定夹角的情况下，弯曲波分裂成以快、慢速度传播的两种模式波，能够接收到较强幅度的正交分量信号.

以上分析表明，同电缆测井条件下各向异性地层井孔中偶极子声源激发的声场类似，随钻条件下偶极子声源激发的弯曲波也存在分裂现象，且βT=0°时偶极子声源激励的弯曲波的速度大于βT=90°时偶极子声源激励的弯曲波的速度.

4.3 快横波面的确定

快横波面定义为快横波偏振方向与井轴确定的平面.采用各向异性分析方法，通过四分量偶极子波形的旋转，从模拟得到的阵列波形中提取了快横波面的方位，通过对比反演得到的方位角同正演模型采用的方位角，分析采用随钻正交偶极子测井进行快横波面方位测量的可行性.

图8为α=90°井内，在快横波面同声源偏振方向的夹角βT=68.75°的情况下，通过Alford四分量波形旋转方法[12］得到的正交分量相对能量随仪器旋转角度的变化图，其极小值对应着目的快横波面方位.正交分量的相对能量定义为正交分量波形能量占四分量波形总能量的比例.从图8中反演得到的快横波面同声源的偏振方向的夹角β′T为69.71°.

2.2.1 设置数据驱动页面 数据驱动页面(Data Driven Pages)是通过设置索引图层生成多个输出页面的方法。索引图层用于通过单个布局生成多个输出页面，每个页面显示不同范围的数据，范围由索引图层中的要素定义[2]。

图9为采用图8所示方法从模拟得到的阵列波形中反演得到的快横波面的方位同模型实际采用的方位的对比图，其中实线为模拟时实际的快横波面同声源的偏振方向的夹角βT，空心圆圈为从数值模拟的波形中反演得到的声源的偏振方向同快横波面的夹角β′T.从图9中可见，反演得到的快横波面方位同模型实际的方位一致性非常好.数值模拟结果证明，在随钻条件下采用正交偶极子声波测量方式能够对地层的快横波方位进行评价.在这一点上，随钻条件下的正交偶极子声波测井同电缆测井情况一致.

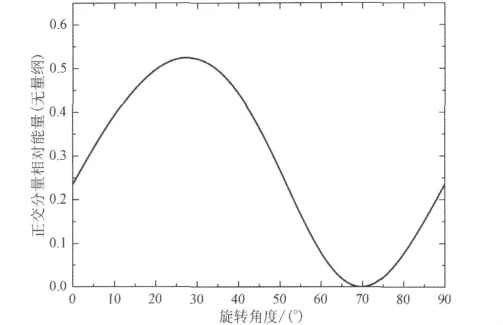
图8 α=90°井内，βT=68.75°情况下，正交分量相对能量随仪器旋转角度变化图Fig.8 The relative energy of cross-line component waveforms with the changes of rotation angle of tools，whenα=90°，βT=68.75°

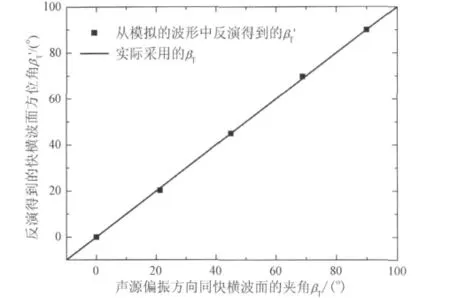
图9 从数值模拟得到的波形中提取的快横波面方位同模型实际的方位的对比Fig.9 Comparison of the fast shear wave direction obtained from simulated waveforms with the actual direction

4.4 频散分析

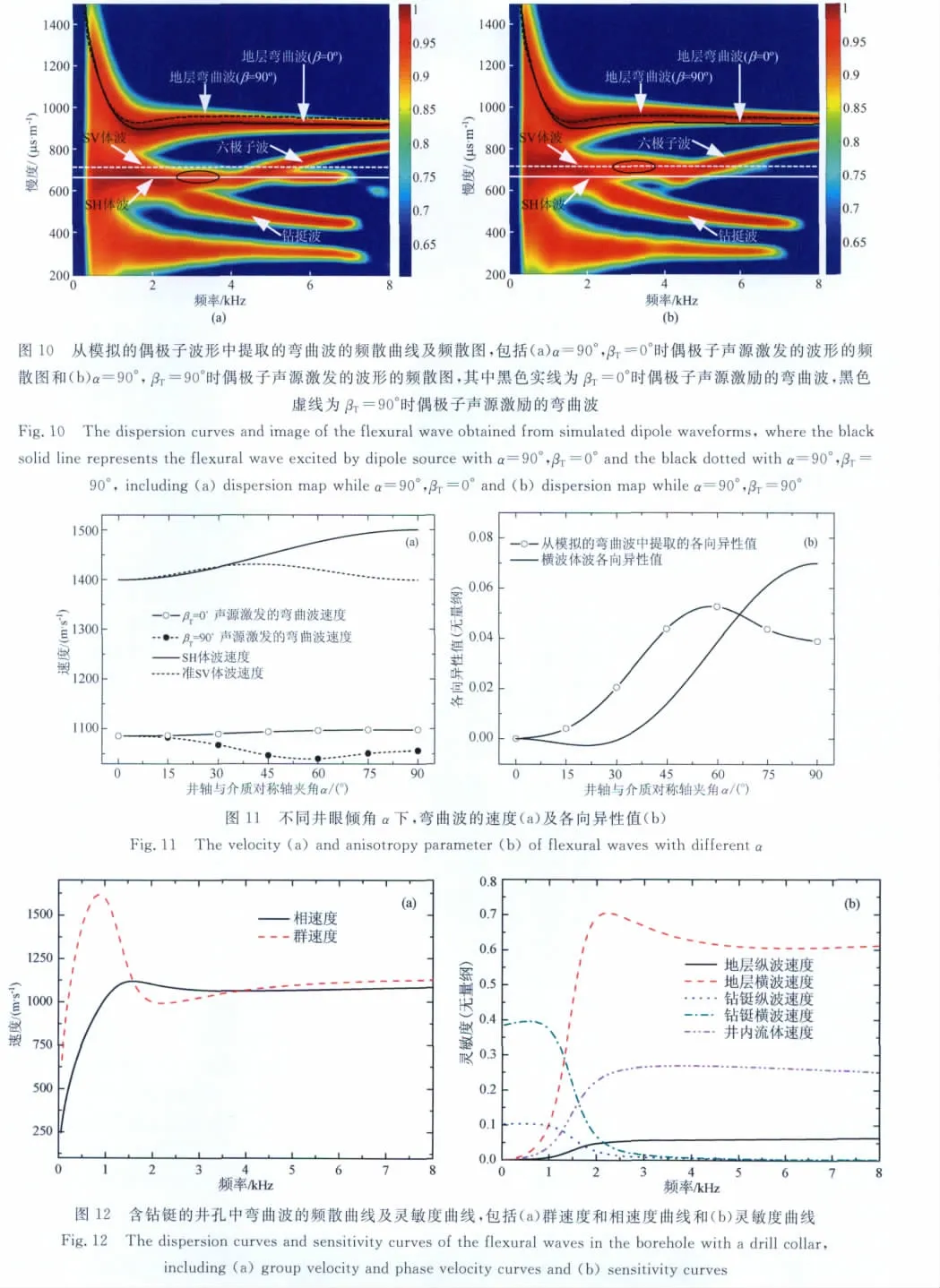
采用矩阵束方法[21］从α=90°，βT=0°、90°时偶极子声源激发的波形中提取了各模式波的频散曲线，提取的结果如图10所示，其中黑色实线和虚线分别为βT=0°、90°时偶极子声源激励的弯曲波的频散曲线，白色实线和虚线分别为该角度下地层体波SH波和SV波的慢度.图10a和图10b分别为βT=0°时偶极子声源激励的声场的频散图和βT=90°时偶极子声源激励的声场的频散图.人们在HTI地层井孔中的数值模拟结果表明，对于电缆测井，在大多数情况下，弯曲波的低频传播速度接近于对应的快、慢横波的传播速度[10，15］.从图10可见，与电缆测井相比，随钻条件下的弯曲波的频散规律有两点不同：在随钻条件下，弯曲波的低频速度并非趋近于地层的横波速度；弯曲波随着频率的变化并非单调变化.对于低频段（0～1kHz）的弯曲波，其速度随着频率增加而增加，且βT=0°时偶极子声源和βT=90°时偶极子声源激发的弯曲波的速度差异不大；在频率1.5～8kHz下，βT=0°时偶极子声源激发的弯曲波的速度大于βT=90°时偶极子声源激励的弯曲波的传播速度，二者差异较大，同电缆测井情况一致.数值模拟的结果表明，对于我们所研究的地层，由于在随钻条件下弯曲波的低频速度不再趋近于地层的横波速度，无法通过弯曲波的测量直接获得地层横波速度；不过，在某些频段内βT=0°时偶极子声源激发的弯曲波的速度大于βT=90°时偶极子声源激发的弯曲波的速度，地层弯曲波的各向异性仍然能够反应地层横波速度的各向异性.

在图10中，可以观察到随频率增加慢度变小的钻铤波和随频率降低慢度逐渐趋近于地层横波慢度的六极子波.之所以能够接收到六极子波，是因为在本文的模拟中，偶极子声源装在钻铤的外侧，极距较大，对于近场而言并非理想的偶极子源，激发的模式波中含有六极子和更高极性的成分[17］.另外一点，在图10所示的频散图中，我们观察到了以地层横波的速度传播的模式（图中圆圈标注区域）.该模式在整个计算的频率段内都能够观察到，在低频段和钻铤波混合在一起，难以区分.该模式的速度同地层横波速度一致，当βT=0°时，该模式的速度同地层的SH波一致；当βT=90°时，该模式的速度同地层的SV波速度一致.SV波的速度为1399.3m／s，小于本文模型中的井内流体速度1500m／s，这说明，该模式能够在软地层中激励.通过对于该模式波速度的提取，可以直接获得地层横波时差及横波速度的各向异性值.在偶极子声源激发的六极子模式波中，未观察到明显的与地层各向异性相关的信息.

4.5 速度提取

数值模拟了α=0°、15°、30°、45°、60°、75°、90°，βT=0°、90°情况下偶极子声源激发的声场，采用慢度时间相关法（STC）提取了同向分量弯曲波的速度.图11a为提取的弯曲波的速度与介质的体波速度的对比图，其中实线为对应偏振方向的体波的速度，实心圆圈和空心圆圈标注的曲线为弯曲波的速度.对于α=90°的井，βT=0°和βT=90°时模拟得到同向分量弯曲波的速度为1098.1m／s和1056.3m／s，均小于对应的体波的速度1500.6m／s和1399.3m／s.从图11a可见，随α变化，弯曲波的速度同体波速度变化趋势不完全一致.βT=0°时偶极子声源激励的弯曲波的速度随α的增加而增加，同地层SH体波的速度变换趋势基本一致，βT=90°时偶极子声源激励的弯曲波的速度随α的增加先减小后增加，而地层准SV体波的速度随α先增加后减小，二者变化趋势不一致.

He等的研究结果表明，在电缆测井情况下，对于大多数横向各向同性地层，弯曲波的低频传播速度接近于对应的地层横波的速度，且随井斜倾角的变化同地层体波的变化基本一致[15］.而在随钻条件下，对于本文所研究的地层模型，弯曲波的速度远小于地层横波速度，且二者的变化趋势也不一致.

通过式（22）计算了不同角度下通过弯曲波测得的各向异性值，其中时偶极子声源激励的弯曲波速度时偶极子声源激励的弯曲波的速度.图11b中的空心圆圈和实线分别为通过弯曲波计算的各向异性值和地层真实的横波速度的各向异性值.从图11b中可见，在斜井随钻条件下采用弯曲波获得的各向异性值同地层的真实各向异性值差别很大：当井轴方向同介质对称轴方向的夹角α小于45°时，采用弯曲波获得的各向异性值远大于地层的真实的各向异性值；当α大于45°时，随着α的增加，二者逐渐接近，在α为65°左右时，二者的值相当，然后随α的增加，二者差异变大.当α大于60°时，虽然二者随α的变化趋势不一致，但是弯曲波的各向异性值基本能够反映地层横波速度的各向异性.此种情况下，可以考虑采用合适的反演方法来获取地层的各向异性信息.

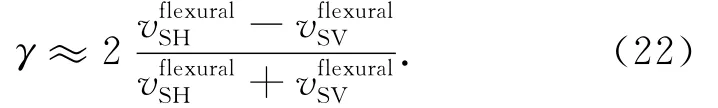
4.6 灵敏度分析

模式波关于某参数p的灵敏度定义为归一化后的波的相速度对该参数的偏微分，见式（23）[1］.通过灵敏度分析可以帮助理解各参数对模式波速度的影响程度.由于各向异性地层井孔声场不存在解析解，本文选取各向同性地层参数来分析随钻测井声学模型各参数对弯曲波速度的影响程度.选取的地层纵横波速度分别为3227.2m／s和1399.3m／s，其它模型参数同上文中的各向异性地层模型的一致.图12a和图12b分别为理论计算的相速度曲线、群速度曲线和各参数（地层纵波速度、地层横波速度、钻铤纵波速度、钻铤横波速度、井内流体速度）的灵敏度曲线.从图12a可见，理论相速度曲线的变化规律与从数值模拟得到的频散曲线的变化规律一致.从图12b灵敏度曲线可见，在随钻条件下，地层横波对弯曲波的控制作用相对电缆测井减小，弯曲波除了受地层横波控制之外，还受到钻铤和其它地层参数的影响.对于本文的模型，在低于1kHz的频率内，钻铤横波速度为弯曲波的最主要的控制因素；在高于1.5kHz内，地层横波速度是影响弯曲波的最主要因素.这解释了图10中在低频段（0～1kHz）βT=0°时偶极子声源和βT=90°时偶极子声源激发的弯曲波速度基本无差异，而在高频段（1.5kHz）二者差异较大的现象.这说明，尽管弯曲波的低频速度并非接近地层横波速度，但是仍旧可以考虑结合理论的频散曲线从弯曲波频散信息中提取地层的横波速度.对于各向异性地层，可以考虑首先选择合适的频率区间，然后分别从快、慢弯曲波波形的频散信息中提取出地层的快、慢横波速度，进一步地可以计算地层横波速度的各向异性值.

5 讨 论

在随钻条件下，由于钻铤的存在，充液井孔中传播的模式波的特征与电缆测井非常不同[1，4，17］，地层声学各向异性在正交偶极子声波测井中的响应特征也与电缆测井不同.本文的模拟结果验证了井孔与TI介质对称轴垂直情况下，采用随钻正交偶极子声波测井方式进行地层快横波方位角评价和地层横波速度的各向异性评价的可行性.另外，在以下几个方面，还需要进行进一步的研究工作.

同电缆测井相比，随钻条件下的弯曲波的传播速度在低频范围内并非趋近于地层的横波速度，无法实现直接横波测井.尽管上文中证实了地层横波速度在一定的频率区间内仍是影响弯曲波的最主要因素，可以考虑采用结合正演模型的反演方法来提取地层的快、慢横波速度及各向异性值，但是正演模型的误差，正演模型输入参数的误差以及测量的弯曲波速度的误差等都可能导致反演得到的横波速度及各向异性值存在较大的误差.可以考虑结合四极子声源的测量结果或者偶极子波形中的六极子模式的处理结果，对地层的快、慢横波速度及各向异性值进行联合反演，这会在一定程度上提高反演结果的可靠性.另外，建立适用于反演的随钻条件下的TI地层井孔多极子声源激发模式波的频散模型是实现上述反演算法的关键.

当井孔与TI介质对称轴存在一定夹角时，情况变得非常复杂，很难应用于现场资料的解释.虽然，当α大于60°时，弯曲波的各向异性值能够基本反映该角度下地层横波速度的各向异性，但是目前的随钻测井技术很难准确测得α，仍旧不能够得到地层真实的快、慢横波速度及横波速度的各向异性值.另外，当α大于60°时，弯曲波的各向异性值同地层真实横波速度的各向异性值随α的变化趋势也不一致，这也给反演结果带来了一定的不确定性.

在图10的频散分析结果中，我们观察到了以地层横波速度传播的模式波，而且对于βT=0°的偶极子声源，该模式波速度与地层SH波一致，对于βT=90°的偶极子声源，该模式波速度同地层SV波一致.这意味着，可以通过偶极子声源实现直接横波测量和各向异性测量.不过该模式幅度相对较低，受钻铤波以及钻进过程中的噪声影响较大，如果想实现工程化应用，需要在隔声、采集以及信号处理方面做进一步的工作.

本文的研究中未涉及钻进过程中的噪声、仪器的偏心以及钻铤波对测量结果的影响，实际测井情况下，这些因素对测量结果有着较大的影响[1］.针对这些问题，需要在仪器设计及信号处理等方面进行进一步的研究工作.

6 总 结

我们采用三维有限差分方法对TI地层井孔中随钻正交偶极子声波测井进行了数值模拟，通过慢度时间相关法、频散分析方法及各向异性分析方法对模拟得到的波形进行了分析，验证了在随钻条件下的HTI地层井孔中进行横波速度的各向异性评价以及快横波方位测量的可靠性，并对介质对称轴同井轴斜交情况下偶极子声源激发的声场进行了计算，主要得到以下认识：

（1）在随钻测井条件下，对于井轴与TI地层对称轴垂直的情况，当偶极子声源偏振方向同介质对称轴呈一定夹角时，井孔中的弯曲波能够分裂成以快慢两种速度传播的模式波，证实了钻铤存在情况下各向异性地层井孔内的弯曲波分裂现象.通过对模拟得到的四分量偶极子波形的处理证实了正交偶极子测量方式评价地层快横波方位的可行性.

（2）在介质对称轴同井轴斜交情况下的TI地层井孔内，偶极子声源激发的声场非常复杂.不过，当α大于60°时弯曲波的各向异性值基本能够反映地层横波速度的各向异性.

（3）随钻条件下井孔内弯曲波频散特征同电缆测井情况下的频散特征非常不同，但是在某些频率区间内，地层横波速度仍然是控制弯曲波的最主要的因素.实际测量时，由于钻铤模型固定，可以考虑选择与正演理论相结合的反演算法来提取地层的快、慢横波速度及各向异性值.

（4）频散分析结果显示，偶极子波形中存在以地层横波速度传播的模式，而且该模式的速度与声源的偏振方向有关.对于βT=0°的偶极子声源，该模式波速度与地层SH波一致，对于βT=90°的偶极子声源，该模式波速度同地层SV波一致.这意味着，可以通过偶极子声源实现直接横波测量和各向异性测量.

致 谢 感谢匿名审稿专家提出的宝贵意见和建设性建议.

（References）

[1]Tang X M，Cheng C H A.Quantitative Borehole Acoustic Methods.San Diego：Elsevier Science Publishing Co.Inc.，2004.

[2]Minear J，Birchak R，Robbins C，et al.Compressional slowness measurements while drilling.／／ 36thAnnual Logging Symposium Transactions，Society of Professional Well Log Analysis，1995.

[3]Leggett J VIII，Dubinsky V，Patterson D，et al.Field test result demonstrating improved resl-time data quality in an advanced LWD acoustic system.SPE Annual conference and Exhibition，New Orleans，Louisiana，USA，2001.

[4]Tang X M，Wang T，Patterson D.Multipole acoustic logging-while-drilling.／／72ndAnn.Internat.Mtg.，Soc.Explor.Geophys.，Expanded Abstracts，2002：364-368.

[5]Sinha B K，Simsek E，Asvadurov S.Influence of a pipe tool on borehole modes.Geophysics，2009，74（3）：E111-E123.

[6]Wang T，Tang X M.LWD quadrupole shear measurement in anisotropic formations.／／73ndAnn.Internat.Mtg.，Soc.Explor.Geophys.，Expanded Abstracts.

[7]乔文孝，王瑞甲，车小花等.利用国产多极子声波测井仪评价地层各向异性的实例分析.声学技术，2008，27（5）：270-271.Qiao W X，Wang R J.Che X H，et al.Case study of anisotropy evaluation by homemade multipole acoustic logging tool.Technical Acoustics （in Chinese），2008，27（5）：270-271.

[8]Chen N Y，Toksöz M N，Cheng C H.Borehole wave propagation in isotropic and anisotropic media：threedimensional finite difference approach.Department of Earth，Atmospheric，and Planetary Sciences，MIT，1994.

[9]Schmitt D P.Acoustic multipole logging in transversely isotropic poroelastic formations.JASA.1989，86（6）：2397-2421.

[10]Sinha B K，Simsek E，Liu Q.Elastic-wave propagation in deviated wells in anisotropic formations.Geophysics，2006，71（6）：D191-D202

[11]张海澜，王秀明，张碧星.井孔中的声场与波.北京：科学出版社，2004.Zhang H L，Wang X M，Zhang B X.Acoustic Field and Waves in Borehole （in Chinese）.Beijing：Science Press，2004.

[12]陈雪莲，王瑞甲.径向分层TI孔隙介质井孔中激发的模式波的数值研究，地球物理学报，2008，51（4）：1270-1277.Chen X L，Wang R J.A numerical study on the mode waves excited by multipole sources in the fluid-filled borehole in radially layered transversely isotropic porous medium.Chinese J.Geophys.（in Chinese），2008，51（4）：1270-1277.

[13]陈雪莲，王瑞甲.横向各向同性弹性地层井孔中模式波的探测深度.吉林大学学报 （地球科学版），2008，38（3）：502-507.Chen X L，Wang R J.Investigating depth of mode waves in the borehole surrounded by transversely isotropic elastic formation.Journal of Jilin University（Earth Science Edition）（in Chinese），2008，38（3）：502-507.

[14]He X，Hu H S，Guan W.Fast and slow flexural waves in a deviated borehole in a homogeneous or layered anisotropic formation.Geophys.J.Int.，2010，181：417-426.

[15]He X，Hu H S.Borehole flexural modes in anisotropic formations：The low-frequency asymptotic velocity.Geophysics，2009，74（4）：E149-E158.

[16]闫守国，宋若龙，吕伟国等.横向各向同性地层斜井中正交偶极子激发的声场的数值模拟.地球物理学报，2011，54（9）：2412-2418.Yan S G，Song R L，LüW G，et al.Numerical simulation of acoustic fields excited by cross-dipole source in deviated wells in transversely isotropic formation.Chinese J.Geophys（in Chinese），2011，54（9）：2412-2418.

[17]崔志文.多孔介质声学模型与多极源声电效应测井和多极随钻声测井的理论与数值研究[博士论文］.长春：吉林大学，2004.Cui Z W.Theoretical and numerical study of modified Biot′s models，acoustoelectric well logging and acoustic logging while drilling excited by multipole acoustic sources[Ph.D.thesis］（in Chinese）.Changchun：Jilin University，2004.

[18]Chew W C， Liu Q H.Perfectly matched layers for elastodynamics：A new absorbing boundary conditions.J.Computat.Acoustics，1996，4：341-359.

[19]梁锴.TI介质地震波传播特征与正演方法研究[博士论文］.东营：中国石油大学 （华东），2009.Liang K.The study on propagation feature and forward modeling of seismic wave in TI media[Ph.D.thesis］（in Chinese）.Dongying：China University of Petroleum （East China），2009.

[20]Schneider J B，Wagner C L，Broschat S L.Implementation of transparent sources embedded in acoustic finite-difference time-domain grids.J.Acoust.Soc.Am.，1998，103（1）：136-142.

[21]Ekstrom M P.Dispersion estimation from borehole acoustic arrays using a modified matrix pencil algorithm.／／Proceedings of the 29th Asilomar Conference on Signals，Systems and Computers.IEEE Computer Society，1995：449-453.