深基坑位移变形监测预测模型分析及应用

叶亚林，付丽丽

(深圳市勘察研究院有限公司，广东深圳 518026)

1 引言

随着我国城市建设的飞快发展，出现了越来越多的深基坑工程。特别是近年来各大城市掀起的高程建筑及地铁建设高潮，形成的深基坑工程规模和难度日益增大。而在密集建筑群之间的深基坑开挖，必然引起各种变形，不仅基坑自身存在位移变形，而且，基坑周围地层及建筑物的地基也会产生沉降和倾斜效应。为了监视基坑的安全，必须对基坑进行位移观测，尤其在地质条件较差的情况下，在深基坑施工时，应加强对基坑特定方向的坡体或支护顶的水平位移监测。而深基坑工程变形的监测和预报作为信息化施工的关键，也是深基坑工程中的重要研究课题之一。

在监测数据正确的情况下，对地表位移变形趋势的拟合与预报，其关键是对监测模型的选取。目前，变形监测预报模型有很多，如回归分析模型、时间序列分析模型、人工神经网络模型、Kalman滤波模型、灰色理论分析模型等。对于同一深基坑工程，采用不同的模型进行拟合预测，其预测精度将会产生很大的不同。因此，只有找到与工程实际规律最为吻合的模型，才能正确预测其发展趋势，因此，本文主要结合深圳市某一深基坑工程的部分监测资料，采用BP网络模型和GM(1，1)模型进行建模，以MATLAB为平台，对部分监测点位移进行分析预测，以便找到最吻合的预测模型。

2 工程实例及相关模型分析

深圳市某公寓工程拟修住宅楼A、B、C栋及幼儿园，其中住宅楼，26层～27层，楼高约 80 m，幼儿园1座，3层，楼高约11.5 m。基础拟采用冲孔灌注桩。设2层地下室，实际基坑开挖深度主要为 7.90 m～10.90 m。按设计要求，沿基坑顶根据周边情况每隔20 m左右设置一个水平位移观测点，共布设31个坡顶水平位移监测点。

根据设计方案对周边地表布点进行观测，以变形观测点S1的1期～30期的水平位移观测数据为依据，进行建模的拟合或仿真分析，并在此基础上选出适合的模型，预测该点31期～33期的水平位移变形量。

2.1 GM(1，1)模型

GM(1，1)是灰色预测模型的一种，它是一组用微分方程给出的数学模型。设变形监测网中某一监测点的各期数据组成时间序列x(0)=［x(0)(1)，x(0)(2)，…，x(0)(n)］，对原始数据序列x(0)作一次累加生成新的序列 x(1)=［x(1)(1)，x(1)(2)，…，x(1)(n)］，其中 x(1)(i)=(k)，则GM(1，1)的白化形式方程为:

这是一阶一元的微分方程模型，其中a，u是待识别的参数。式(1)解的离散形式为:

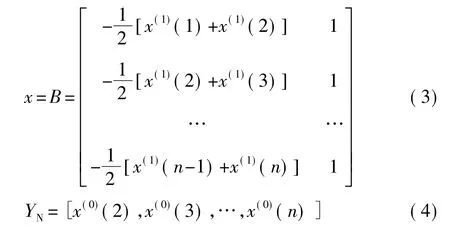
得变量x(0)(k)的GM(1，1)模型计算值，即:

式中 k=(1，2，3，…，n)。

GM(1，1)模型对该基坑变形观测点S1的1期～30期的观测数据的拟合值及误差如表1所示，图1、图2分别为该模型的拟合曲线图及误差曲线图。从曲线图可知，该模型的拟合值比实际监测值偏大，误差比较大，拟合精度不高。

GM(1，1)模型、曲线拟合模型与BP模型拟合仿真值及误差 表1

图1 GM(1，1)模型拟合曲线图

图2 GM(1，1)模型拟合误差曲线图

2.2 曲线拟合模型

曲线拟合是趋势分析法中的一种，又称线性回归或趋势曲线分析，也是比较常用的定量预测方法之一，本文应用的是曲线拟合的最小二乘法。

由已知的离散数据点选择与实验点误差最小的曲线

称为曲线拟合的最小二乘法。

若记:

其中:

它的平方误差为:

图3、图4分别为曲线拟合模型的拟合曲线图及误差曲线图。该模型对该基坑变形观测点S1的1期～30期的观测数据的拟合值及误差如表1所示，从曲线图可知，该模型的仿真值与实际监测值的误差比GM(1，1)模型的要小，精度较之 GM(1，1)模型也有所提高。

图3 曲线拟合模型拟合曲线图

图4 曲线拟合模型误差曲线图

2.3 BP网络模型

BP模型是人工神经网络模型，它一般由输入层、隐含层和输出层三部分组成，隐含层可以是1层也可以是多层。图5所示即为一个3层BP网络结构。采用BP网络的学习过程是由正向传播和反向传播组成的，正向传播是输入信号从输入层经过隐层，传向输出层，若输出层得到了期望的输出，则学习算法结束;否则，转至反向传播。反向传播是将误差信号沿原连接路径反向计算，并通过修改各层神经元的连接权值，使误差信号减小。经实践表明，这种基于误差反传递算法的BP网络具有很强的映射能力，可以解决很多实际问题。

图5 3层BP网络

参照图5所示的BP网络结构，设网络的输入为X=(x1，x2，x3，…，xn)，目标输出 D=(d1，d2，d3，…，dm)，而实际输出为 Y=(y1，y2，y3，…，ym)，其网络的学习步骤一般为:

(1)用均匀分布随机数将各权值设定为一个小的随机数，作为节点间接权的初值和阈值;

(2)计算网络的实际输出Y;

(3)由输出节点 j(j=1，2，3…m)的误差:ej=djyj，计算所有输出节点误差平方总和，得能量函数:

如果E小于规定值，转步骤(5)，否则继续步骤(4)。

(4)调整权值;

(5)进行下一个训练样本，直至训练样本集合中的每个训练样本都满足目标输出，则BP网络学习完成。

BP模型对该基坑变形观测点S1的1期～30期的观测数据的仿真值及误差如表1所示，图6、图7分别为该模型的仿真曲线图及误差曲线图。从曲线图可知，该模型的仿真值与实际监测值非常接近，误差较小，在3个模型中，BP模型的精度是最高的。

图6 BP模型仿真曲线图

图7 BP模型训练后误差曲线图

3 监测数据拟合及分析

从表1和图8可知，BP网络模型拟合及预测最为准确，其次是曲线拟合模型，最后才是GM(1，1)模型。拟合曲线是基于观测值服从正态分布的，因此变形监测点的观测次数不宜太少，GM(1，1)模型拟合值比实际监测值偏大，可用于对工程变形进行提前报警，以便及时加强基坑支护，防止连续墙及支撑钢管过度变形而导致基坑塌陷，BP网络模型的仿真值精度最高。

图8 各模型拟合仿真值

4 采用BP模型进行预测

通过上述分析，本文采用BP模型对该深基坑进行位移变形量的预测。结合MATLAB编写预测代码如下:

根据前面用BP模型做的仿真训练，来预测该点的位移变形量。用前3期(28、29、30期)的位移变形量，预测31期的位移变形量。本文共预测了该点未来3期(31期～33期)的位移变形量，32、33期的预测步骤与预测31期相同，预测结果见表2，预测值与实测值对比结果如表3所示。

BP模型对该基坑水平位移变形量的预测结果 表2

BP模型预测值与实测值对比结果 表3

由表3可以看出，预测值与实测值的误差比较小，预测结果比较可靠。

5 结语

通过对GM(1，1)模型、曲线拟合模型以及BP网络模型3种模型的介绍及应用可以看出，在处理同类型的数据时，BP网络模型仿真值及精度最高，曲线拟合模型及GM(1，1)模型拟合值和拟合值及精度远不及BP网络模型，因此，本文采用BP网络模型作为处理深基坑位移变形监测数据的主要模型，对某一深基坑进行位移变形量的仿真及预测。

［1］董长虹.MATLAB神经网络与应用［M］.北京:国防工业出版社，2007

［2］侯媛彬，杜京义，汪梅.神经网络［M］.西安:西安电子科技大学出版社，2007

［3］黄声享，尹晖，蒋征.变形监测数据处理［M］.武汉:武汉大学出版社，2010

［4］赵言，花向红，翟高鹏.GM(1，1)与自回归模型在位移监测中的应用［J］.城市勘测，2011(3):115～118

［5］贺跃光.工程开挖引起地表移动与变形模型及监测技术研究［D］.长沙:中南大学，2003

［6］朱海国，尹晖，陈雪丰.地铁变形监测中曲线拟合与自回归模型的综合应用［J］.测绘与空间地理信息，2006，29(6):89～91