AutoCAD中判断折线自相交的一种快速算法
2012-09-22周建康冷泠王瑞青
周建康,冷泠,王瑞青
(郑州市规划勘测设计研究院,河南郑州 450052)
1 引言
折线自相交是地理信息系统空间线性数据处理中的一个比较重要、常见和复杂的问题,
在地图综合、空间分析、CAD数据向GIS数据转换等诸多领域有着广泛的应用。例如,空间分析中常见的多边形缓冲区分析,既要求参与分析的多边形不能存在自相交现象,又要求生成的缓冲区多边形不能存在自相交情况。但是,由于空间数据的复杂性与多样性,在实际数据生产与应用中,不可避免地会产生折线自相交。因此,设计一种快速判断并定位折线自相交的算法是地理信息系统设计中需要解决的问题。国内外一些学者对此问题进行了相关探讨和研究,也取得了一些成果[1~3],这些算法作为通用算法可以初步解决折线自相交的判断问题。但在应用到数据生产中时,由于没有结合具体的系统平台特点,不仅在算法上无法做到最优,同时在面对复杂和海量的空间数据时效率低下,无法满足生产需求。
AutoCAD作为CAD默认行业标准,在我国很多行业有着广泛应用。一方面在城市规划、测绘等领域,各单位存在大量的DWG数据及许多基于AutoCAD的应用系统;另一方面,在基础地理信息数据的采集中,AutoCAD或基于AutoCAD的数据采集平台被广泛使用,AutoCAD支持下的地形图数据和其他行业数据成为城市基础地理信息系统和专业地理信息系统建设的主要数据源。因此,在AutoCAD中解决折线自相交的快速判断,可以有效保证数据的质量,为数据的GIS应用奠定基础。但从目前现状看,包括很多商业软件在内都没有很好地解决或者避开该问题。
2 折线自相交判断的一般算法
自相交判断的一般算法是基于折线自相交问题的定义提出的。
2.1 折线自相交问题定义
设有折线 l={p1,p2,…,pn},(i=1,2,…,n),pi是折线上顺次连接线段的端点。若除了相邻线段间的连接端点p1,p2,…,pn外,折线上的线段还存在其他交点,则定义此折线为自相交折线。
2.2 判断折线自相交的一般算法
判断折线自相交一般都是采用以下算法或者基于此算法演变而来。
对于折线l上的线段,按照其连接顺序分解为多条两点组成的线段,两两判断这些线段是否相交,根据交点情况和自相交的定义来判断折线l是否自相交,如果自相交则求出自相交交点,这就将问题转化为两线段的相交问题。两线段的相交判断采用以下方法:
设有两条线段 K1(p1,p2)、K2(p3,p4),欲求其交点,需要先判断它们是否相交,为此设:

若 x1max<x2min或 y1max<y2min或 x1min>x2max或 y1min>y2max则K1、K2不相交;否则,需要进一步判断,为此设:

p1p2的直线方程为 f(x,y)=dx(y-p1.y)-dy(xp1.x)=0。凡在 p1p2上的点必满足 dx(y-p1.y)-dy(x- p1.x)=0,而其他点使 dx(y-p1.y)-dy(x-p1.x)≠0,且在直线两侧的半平面内的点使上式异号。因此,判断p3、p4在K1不同侧的充分必要条件是:f(p3.x,p3.y)*f(p4.x,p4.y)≤0。若两个线段的端点都在对方的不同侧,则此两线段相交。
该算法的优点是简单、直观;缺点是计算烦琐、运算量大,在时间上不是最优。
3 基于AutoCAD的折线自相交快速判断算法
AutoCAD中的折线是指其对象类型中的多段线。多段线的组成包括直线段或圆弧段,采用上文的一般算法不仅需要计算线段的交点,还可能需要圆弧的交点,运算量相当大,尤其是当数据量大时,运算时间上是无法忍受的。因此,本文在分析AutoCAD数据结构和Offset(偏移)方法的基础上,利用其自身处理原则,快速地实现了多段线自相交的判断和相交点定位。
3.1 AutoCAD的Offset方法分析和折线自相交判断算法依据
Offset方法是AutoCAD提供的一种平行线创建方法。平行线创建算法也是计算几何中研究比较多的一个算法,尤其是在处理平行线创建过程中产生的自相交情况。AutoCAD只提供了Offset操作和该操作的二次开发接口,没有提供该方法的核心算法说明,经数据多种情况操作试验分析,得出了其处理的过程和基本原则。
第1步,判断多段线的方向。AutoCAD中的多段线有顺时针方向和逆时针方向之分,对于顺时针方向,Offset方法的距离值为正值时为向内偏移,距离值为负值时为向外偏移;对于逆时针时刚好相反。这里可以简单理解为创建平行线时根据偏移距离的正负,Offset方法会根据预定义规则往多线段前进方向的同侧(左侧或右侧)偏移创建平行线(图1,多段线L的方向如图所示,偏移距离为+10 mm)。
第2步,将多段线分解成相邻两点构成的线段,根据多段线的方向,对每段线段分别创建平行线(图1中虚线,这里所有平行线一定都在L前进方向的右侧)。
第3步,根据原始多段线的线段顺序,对生成的每段平行线按顺序进行连接或裁剪处理,生成最终平行线。具体连接或裁剪的原则为:连接或裁剪时按照原始多段线的前进顺序,对平行线段的首尾进行处理。相邻的平行线段如果相交,则裁剪删除掉相交点外多余的部分(图2中A点虚线部分),如果不相交,则延长至相交连接(图2中B、C、D虚线部分),如果延长不相交(自相交或偏移距离过大),则该段无法创建平行线(图4中BC段与CD段重叠自相交,创建的平行线段不相交,则在此段无法创建平行线,此段之前的平行线段也会被舍弃,最终只能生成平行线ab);如果平行线与原始多段线相交,则从临近原始多段线一侧偏移距离处裁剪删除(图2中E、F点距离L线10 mm)。
第4步,最终生成平行线。根据处理原则可以分析出,“叶形”自相交(除自相交点外自相交部分都不在线上)Offset后会产生多条平行线(如图3,产生2条);“回头线”自相交(自相交部分完全与线本身重合)只产生一条平行线,但平行线节点数一定少于原始多段线(如图4平行线ab)。
需要注意:偏移距离不能过大,过大可能会导致平行线无法创建。

图1 分段创建平行线段 图2 处理平行线段为平行线 图3 Offset方法最终结果图
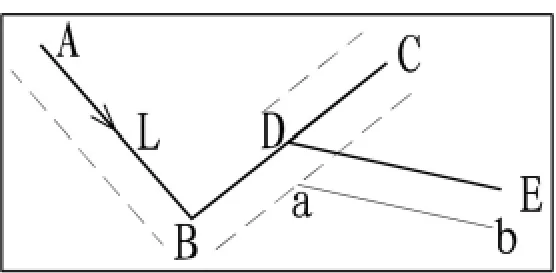
图4 “回头线”自相交Offset图
经过以上分析,我们可以得出结论:在尽可能小的偏移距离(最好产生平行线直接与多段线近似重叠效果,可以直接避免偏移距离过大造成的平行线创建失败,同时可以方便自相交点的定位)下,Offset方法只有在自相交的情况下,创建平行线数量才会大于一条或者只有一条平行线但平行线的节点数小于原多段线,且多段线自相交点一定位于平行线的首尾处(偏移距离小,平行线的首尾点基本上与自相交点重合)。
3.2 基于AutoCAD的Offset方法的算法
Offset方法创建平行线可以用:

来表示,其中A表示创建的平行线集合,L(t)为初始多段线,d表示平行线偏移距离,n(t)是多段线在参数t处的单位方向向量。
基于上文中的结论,结合式(3),AutoCAD中多段线自相交快速判断算法可以描述为:
第1步:获取需要判断处理的多段线,赋值为对象变量L;
第2步:对L进行Offset操作,偏移距离绝对值d尽量等于0但一定大于0(如0.00001),获得平行线集合A;
第3步:获取集合A的数量A.count;若A.count=1,则比较平行线A(0)的节点数与L的节点数,如果A(0).pointCount=L.pointCount,可判断 L 线无自相交情况,如果 A(0).pointCount<L.pointCount,即可判断 L线存在自相交,且自相交点位置位于A(0)的首尾处;若A.count>1,则可判断L线存在自相交,且自相交点位置位于A集合中所有线对象的首尾点处。
需要注意:当自相交线的平行线集合A中线对象的首尾点位于多段线L的首尾点时,该点可能不是自相交点,但为加快运算速度,不再进行判断,直接标记该点后人工可以快速判断和处理。
第4步:返回自相交和自相交点位置信息,结束运算。
算法流程图如图5所示。
4 结论
AutoCAD中基于Offset方法的折线自相交快速判断算法,无论从算法的空间复杂度上还是时间复杂度上都较一般常规算法有了特别明显地改善,提高了AutoCAD中基础地理信息数据的折线自相交问题的处理效率,解决了一直以来AutoCAD中多段线自相交的快速自动判断和定位问题。采用该算法基于VBA对郑州市规划控制六线50多万条多段线数据的自相交质量检测应用表明,该算法具有实现简单、运算速度快、稳定性好、完善实用等特点。
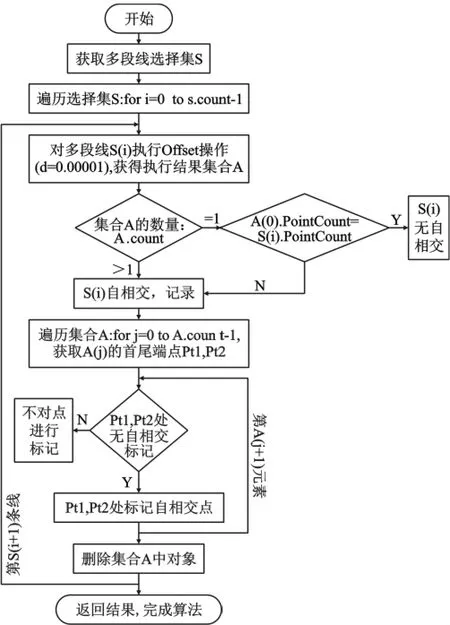
图5 算法流程图
[1]Mark de Berg,Marc van Kreveld,Mark Overmars,et al.Computational Geometry:Algorithm and Applications[M].New York:Springer,1993
[2]杨维芳.判断折线自相交的快速算法[J].兰州铁道学院学报(自然科学版),2002,21(3):76 ~78
[3]周培德.计算几何[M].北京:清华大学出版社,2000
[4]曾洪飞,张帆,卢择临.AutoCAD VBA&VB.NET开发[M].北京:中国电力出版社,2008
[5]郭仁忠.空间分析[M].武汉:武汉测绘科技大学出版社,1997
[6]吴千里,马小龙.面向城市规划信息化的GIS与CAD集成技术探讨[J].测绘通报,2010(2):52~55
