以工学结合为指导 构建高职数学教学新模式

王荣琴

(云南交通职业技术学院 文理学院，昆明 650500)

以工学结合为指导 构建高职数学教学新模式

王荣琴

(云南交通职业技术学院 文理学院，昆明 650500)

为适应高职教育“工学结合”人才培养模式的要求，以建构主义学习理论为指导，研究探索高职“高等数学”课程教学改革。通过引入“数学建模”的思想与方法，构建与“工学结合”的人才培养模式相匹配的高职数学课程教学模式:基于问题的教学模式，改变传统数学课程教与学的活动方式，实施高职数学课程教学改革。

高职教育;高等数学;数学建模;基于问题的教学模式

“高等数学”课程是高职教育中一门重要的文化基础课。随着高职教育的不断发展，课程改革的不断深入，创新以项目、岗位、任务为导向的“工学结合”人才培养模式，高职院校的专业课，实训、实践课的课程体系、教学模式、教学方法已发生了根本性变革，这对高职教育的基础课特别是“高等数学”课提出了新的要求，使高职数学课程的教与学面临着极大的挑战。为适应高职人才培养模式的需求，必须对高职数学课程的教学实施全面改革，深入研究与高职教育人才培养模式相匹配的“高等数学”教学模式。

1 以“工学结合”为指导，研究高职“高等数学”教学模式

1.1 教学模式的概念

“教学模式就是学习模式。在帮助学生获得信息、思想、技能、价值观、思维方式及表达方式时，教师也在教他们如何学习。事实上，教育的最终目的是将来能够提高学生更容易、更有效地进行学习的能力，因为他们不仅获得了知识技能，也掌握了学习过程”。［1］教学模式是一种相对稳定和具有范式意义的教学结构，它是教学理论具体化与教学经验概括化的中介，掌握教学模式有利于人们把握和应用教学过程的本质和规律。

《数学教育学导论》中指出，我国传统数学教学使用最为广泛的教学模式是“五环节教学法:复习—导入—讲解—巩固—小结。”［2］五环节教学模式反映了教师向学生传授知识的过程，是以教师为中心的教学模式。该模式的缺点是忽视了学生在课堂上的主体作用，使学生成为知识学习的被动接受者。

“工学结合”及其相关概念均是基于教育与生产劳动相结合的理论，是以学校与企业合作为具体表现形式的理论知识学习与实践工作的结合。当前“工学结合”成为我国高职教育人才培养模式的主流。由于高职教育的目标是:“培养符合社会经济生产服务第一线需要的高素质高技能型技术应用型人才”，因此，高职教育更加注重学生应用及动手能力的培养。高职数学课程的教学应改革传统教学模式，以“工学结合”的高职教学理念和教学方法为指导，深入研究高职各专业的人才培养目标，合理制定高职数学课程的结构、内容，突出高职教育特色，构建与高职教育人才培养模式相匹配的“高等数学”教学模式，满足高职人才培养的需要。

1.2 建构主义学习理论指导下的教学模式

建构主义代表着当代教育心理学发展的方向和主流，建构主义学习观认为“学习是学习者以自身已有的知识和经验为基础的主动建构活动”［3］。学习并非是一个被动接受的过程，而是学习者以自身已有的知识和经验为基础的主动建构过程，是在一定的情境下，借助其他人的帮助即通过人际间的协作活动，在学生已有的知识和经验基础上，通过个体与周围环境相互作用(同化和顺应)，来实现知识意义构建的过程。因此，建构主义学习理论认为“情境”、“协作”、“会话”和“意义建构”是学习环境中的四大要素。

2 构建基于问题的教学新模式

2.1 以问题为核心

问题是数学的核心。数学课对学生思维能力的培养，应以问题解决为契机，让学生在解决问题的过程中获得知识、发展思维。数学课对学生思维能力的培养，不但要通过解决问题来实现，而且最终以解决问题为目的，这是数学与其他学科相比，在思维能力培养方面最明显的特征。因此，配合高职“工学结合”人才培养模式，根据建构主义学习理论，高职数学课程应按照“提出问题(设计问题情境)—解决问题(建立模型)—意义建构(知识与应用)”的模式实施教学。改变数学课程实施过程中过于强调接受学习、机械训练的现状，充分发挥学生在学习过程中的主体作用，在教学过程中以问题解决为核心，挖掘与实际问题、专业知识结合紧密的知识内容，实现对学生思维的培养，知识应用、交流与合作能力的提高。

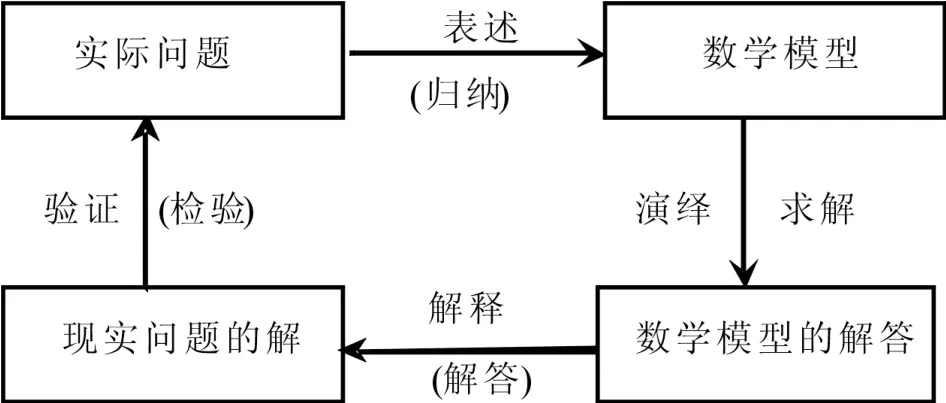
图1 数学建模的过程

2.2 引进“数学建模”的思想和方法

“数学模型”是对于现实世界的一个特定对象，为了一个特定的目的，根据其特有的内在规律，作出一些必要的简化假设，运用适当的数学工具，得到的一个数学结构。数学建模就是建立数学模型的全过程，包括表述、求解、解释、检验等几个阶段，并且通过这些阶段完成从现实对象到数学模型，再从数学模型到现实对象的循环，如图1所示。

将数学建模的思想和方法引入高职数学课程的教学，使数学教学实现由“实践-理论-再实践”的过程，使数学课程的教学与实际问题的解决联系起来，与学生的专业结合起来。有利于提高学生应用数学知识解决实际问题的能力，达到学以致用的目的，使数学课程的教学模式与高职“工学结合”的人才培养模式相匹配。

2.3 基于问题的教学模式

以“问题”为核心，在教学中引入“数学建模”的思想和方法，构建“基于问题的教学模式”，如图2所示。

1)创设问题情境:以问题解决为核心，根据教学内容，挖掘数学课程中与实际问题、专业知识结合紧密的知识内容，创设问题情境。2)确定问题:按照数学建模的思想和方法，根据实际问题建立数学模型，这是将实际问题转化为数学问题的过程。3)解决问题。围绕问题解决，引入数学课程教学内容，通过课堂教学、分析，学生讨论、协作等方式完成数学知识的教学。4)总结反思:通过回顾问题解决的全过程，对数学知识进行概括和总结，达到理解并应用数学知识解决实际问题的目的。

图2 “基于问题的教学模式”的4个教学环节

在这种教学模式中，学生是知识意义的主动建构者;教师是教学过程的组织者、指导者，意义建构的帮助者和促进者;教材提供的知识不再是教师传授的内容，而是学生主动建构意义的对象;教育技术不仅是帮助教师传授知识的手段、方法，而且是学生主动学习的，协作式探索的认识工具。

“基于问题的教学模式”的特点体现在:1)以“问题”引领知识学习，在解决问题中，实现理论知识与实际问题相结合，使数学课程的学习与专业应用相联系。2)在“问题解决”中训练思维、学习知识;在“问题解决”中实现交流与合作，在“问题解决”中感悟数学应用，培养学习兴趣。3)充分体现学生在学习中主体性，有利于提高学生自主学习能力。

2.4 “基于问题的教学模式”的教学案例

在物流专业“导数的应用——函数的最大值与最小值”的教学中，结合物流专业的特点，按照“基于问题的教学模式”实施教学实践的教学案例。

课题:导数的应用——函数的最大值与最小值(教学时间:90分钟)

教学目标:1)知识目标。理解函数的最大值与最小值的概念，掌握函数的最大值与最小值的求法。2)能力目标。学习应用“函数的最大值与最小值”解决实际问题的思想和方法。3)素质目标。培养学生运用所学知识解决实际问题的能力。

教学重点:函数的最大值与最小值概念的理解;应用函数的最大值与最小值思想解决实际问题的思想和方法。

教学过程:首先，创设问题情境。在物流管理过程中，常常会遇到货物、原材料的定货与存储问题。合理化的存储就成为物流管理过程中的重要环节，如何根据实际情况安排批量订货，在满足需要的同时使订货总费用最小?这是经济订货批量问题。

例题1:某商场每月需要某种货物200件，每批订货费为20元，若每批货物到达后先进仓库，每月每件商品的存储费为0.8元，试问，该商场应如何安排订货，可以使每月总平均订货费用最小?

其次，确定问题。经济订货批量问题事实上就是数学中函数的最大、最小值问题。应用数学建模方法提出假设:1)当存货降到零时，立即补货。2)需求是连续均匀的，单位时间的需求量是常数(即需求率)是常数R，则在时间t内的需求量为:Q=Rt。3)每次订货的费用c和单位时间内每单位数量的货物存储费d不变。4)每次定货量相同。

按照数学建模方法建立存储模型:每经时间t补充一次库存(即订货周期为t)，订货量为Q(即批量)，订货量Q必须满足订货周期t内的需求，所以，Q=Rt。设货物的单价为k，每次订货的费用为c，单位时间内每单位数量的货物存储费为d，因此订货总费用为C，则C=c+kQ=c+kRt。于是，单位时间内的订货费为

设y是货物在x时刻的存储量(0≤x≤t)，当0＜x＜t时，不需要补充货物。存储量变化如图3所示。

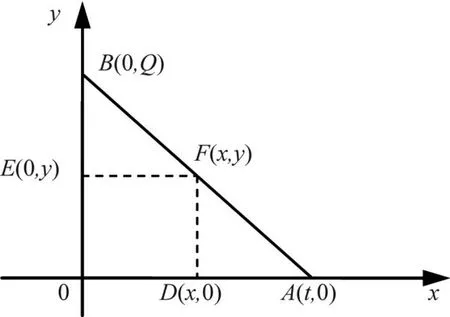
图3 货物在x时刻的存储量函数图

再次，解决问题。通过将实际问题转化为存储模型的问题，切入到“函数的最大值与最小值及其求法”的教学。(教学过程略)

最后，总结反思，总结“求函数的最大值与最小值”思想、方法和步骤并求解例题1。(略)

通过以上教学实例，可以看出:数学教学结合学生所学专业，挖掘数学知识在专业中的运用，采用“基于问题的教学模式”，有利于培养学生应用知识解决问题的能力，更能适应高职人才培养模式的需要。

3 对“基于问题的教学模式”的再思考

1)在“基于问题的教学模式”中，通过4个教学环节，使整个教学经历了由“从实际(问题情境)—理论—再回到实际中运用”的过程。学生在学习新知识时，在教师提供的问题情境引领下，尝试应用已有的知识和经验，从不同角度吸收新知识，最后纳入自己的认知结构中，从而产生有意义建构，教学取得了良好的效果。使学生的学习方式由“听、练”转变为“思考、探索、交流、感悟”，体现了学生学习的主体性。

2)在教学中，应该充分发挥现代教育技术的优势，适当、合理地使用现代教育技术，并非彻底抛弃传统教学方法，而是吸取传统教学方法的长处，对传统教学模式加以改造，将二者在教学中有机地结合起来，优势互补，达到提高教学效率与教学质量的目的。

3)“基于问题的教学模式”，使高职“高等数学”课程的教学与高职“工学结合”人才培养模式相匹配。在“问题解决”中体现学生学习的主体性，实现交流与合作;在“问题解决”中感悟数学应用，体现“做中学、学中做”，突出职业教育特色。

［1］JOYCE B，WELL M，CALHOUN E.教学模式［M］.7 版.荆建华，译.北京:中国轻工业出版社，2009:1，5.

［2］张奠宙，李士锜，李俊.数学教育学导论［M］.北京:高等教育出版社，2003.

［3］郑毓信，梁贯成.认知科学、建构主义与数学教育:数学学习心理学的现代研究［M］.上海:上海教育出版社，2002.

［4］王荣琴.高等数学［M］.北京:高等教育出版社，2009.

［5］姜启源，谢金星，叶俊.数学模型［M］.3版.北京:高等教育出版社，2003.

［6］傅维潼.物流数学［M］.北京:高等教育出版社，2006.

Exploration of New Teaching Mode of Mathematics in Vocationals

WANG Rongqin
(Faculty of Arts＆Sinence，Yunnan Vocational and Technical of Communications，Kunming 650500，China)

The new teaching mode of mathematics in vocational colleges is studied in this paper.The principles of vocational education are described briefly.The focus of this paper is then concentrated on the problem-oriented teaching mode of mathmatics，including the introduction of problems，the ideas and methods of mathematics modeling，the teaching method，and case study.Author’s pracitec has shown the effectiveness of this new teching mode.

Higher vocational education;higher mathematics;mathematical modeling;problemoriented teaching mode

G712.307

A

1008-5440(2012)01-0061-04

2011-12-21

云南省高职教育研究会第2批高职教育科研课题:基于“工学结合”人才培养模式的高职“高等数学”教学改革研究(2011YGZ11)

王荣琴(1966-)，女(汉族)，贵州遵义人，副教授，硕士，研究方向:数学教育教学研究。