基于改进灰色模型的东北地区铁路货运量预测*

张 玥，帅 斌

(西南交通大学交通运输与物流学院，四川成都 610031)

随着“十二五”规划的进一步推进，东北地区再一次成为区域发展的重点。实施东北地区等老工业基地振兴战略以来，东北地区经济社会发展加快，改革开放以来被拉开的发展差距逐年缩小，赶上了全国平均增速。2008年东北三省地区生产总值占全国的比重升至 8.62%，比 2007年高0.14%，这是进入新世纪后东北三省地区生产总值占全国的比重首次止跌回升。交通运输是经济发展的基本需要和先决条件，是资源配置和宏观调控的重要工具，对促进社会分工、大工业发展和规模经济的形成有着重要的影响。而货运量作为交通运输的一个客观反映，它的大小是铁路运输情况的重要体现之一。铁路货物运输与地方经济和企业有着密切关系，并且在东北地区的经济发展中占有重要的地位。铁路货运量预测分析工作是铁路运输工作的重要环节，具有较强的实际意义［1］，并与人均国内生产总值有密切联系(见表1)。

表1 2004—2010年东北地区人均国内生产总值与货运量Table 1 2004－2010 real GDPper capita and freight volume in northeast region

灰色系统即为信息不完全的系统。灰色系统以部分信息已知，部分信息未知的小样本、贫信息的不确定性系统作为研究对象，通过对部分已知信息的生成、开发，以信息覆盖为依据，实现对现实世界的确切描述和认识。灰色系统预测具有预测精准度高、无需大量有规律样本、计算工作量小等优点［2］。灰色GM(1，1)模型是灰色系统预测常用模型之一，适用于具有较强指数规律、过程单调变化的序列。通过对东北地区货运量数据的汇总发现，东北三省货运量呈逐年递增的趋势，符合灰色系统预测数据单调变化的特征要求，因此，选用灰色GM(1，1)模型作为预测东北地区货运量的基本模型。本文在采用灰色GM(1，1)模型的基础上，对预测精度进行严格检验，使其适用于预测东北地区的铁路货运量［3］。自从2003年实施东北地区振兴老工业基地举措以来，经济得到迅猛发展。为了更切实的迎合这一发展趋势，通过运用改进的灰色GM(1，1)模型——新陈代谢模型，更好的预测未来几年里东北地区整体的货运量。

1 建立灰色 GM(1，1)模型［4－6］

(1)设变量 x(0)(k)的原始数据序列为:x(0)(k)=(x(0)(1)，x(0)(2)，…，x(0)(n))对原始数据序列经过一次累加后得到x(0)(k)的1－AGO序列x(1)(k):

x(1)(k)=(x(1)(1)，x(1)(2)，…，x(1)(n))。其中:x(1)(k)=x(0)(i);k=1，2，…，n

(2)将数据代入灰色微分方程x(0)(k)+az(1)(k)=b中，写成矩阵形式，得:Y=Hθ。其中:

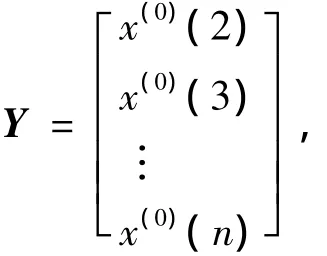
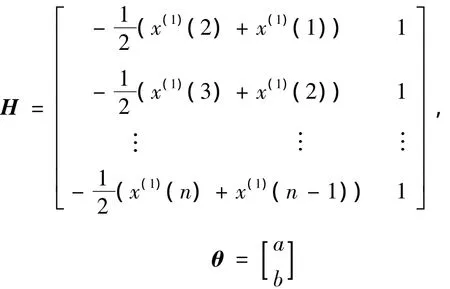
上述方程组中，Y和H为已知，θ为未知参量，可用最小二乘法求的最小二乘解:

(3)由x(1)建立微分方程:+ax(1)=b，其解为:

(4)得到灰色GM(1，1)预测方程:

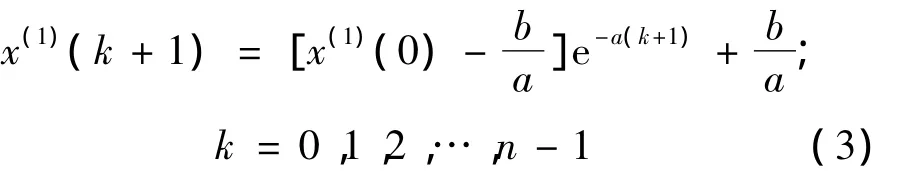
(5)还原值为:

2 建立新陈代谢GM(1，1)模型

基本的灰色 GM(1，1)模型均以叠加序列x(1)(1)作为灰色微分模型的初始条件进行建模的，容易造成对新信息的利用不够充分。新信息优先原理是灰色系统理论的信息观，该原理认为新信息对认知的作用大于老信息的作用，赋予新信息较大的权重可以提高灰色预测的功效，新信息的补充为灰元白化提供了基本动力［8］。根据此原理，本文拟采用以x(0)(k')为初始条件的新陈代谢GM(1，1)模型对东北地区的铁路货运量进行预测。

新陈代谢GM(1，1)模型的建立方法如下:在原始数据序列的基础上置入最新信息x(0)(n+1)，去掉老信息 x(0)(1)，x(0)(2)，…，x(0)(k'－ 1)，建立新陈代谢 GM(1，1)模型的新原始数据序列x(0)(k')=(x(0)(k')，x(0)(k'+1)，…，x(0)(n+1))，继而建立新的叠加序列x(1)(k')=(x(1)(k')，x(1)(k'+1)，…，x(1)(n+1))。其他步骤同上，直至得到预测目标为止。

3 精度检验［7］

3.1 残差检验

设残差为:ε(k)=x(0)(k)－^x(0)(k)，则相对

3.2 后验差检验

设 x(0)(k)=(x(0)(1)，x(0)(2)，…，x(0)(n))为原始数据序列，(0)(k)=(0)(1)(0)(2)，…，(0)(n))为模型模拟序列，ε(0)(k)=(ε(0)(1)，ε(0)(2)，…，ε(0)(n))为残差序列。则x(0)的均值为=x(0)(k)，x(0)的 方 差 为 S21=(x(0)(k)－¯)2;ε(0)的均值为=ε(0)(k)，ε(0)的方差为 S22=(ε(0)(k)－2。

检验标准2:对于给定的C0＞0，当C＜C0时，即为均方差合格模型。

检验标准3:对于给定的p0＞0，当p＞p0时，即为小误差概率合格模型。

3.3 关联度检验

检验标准4:对于给定的ε0＞0，当ε＞ε0时，即为关联度合格模型。

表2 模型检验等级参照表Table 2 Reference table of model test grades

3.4 模型预测效果检验

当a＜2时，GM(1，1)模型有意义，但随着a的取值不同，预测效果也不同:

(1)当a≤0.3时，GM(1，1)模型可用于中长期预测;

(2)当0.3 ＜ a≤0.5时，GM(1，1)模型可用于短期预测，中长期预测慎用;

(3)当0.5 ＜ a≤0.8时，GM(1，1)模型用于短期预测应十分谨慎;

(4)当0.8＜a≤1时，应采用修正 GM(1，1)模型;

(5)当a＞1时，不宜采用 GM(1，1)模型。

4 应用改进灰色GM(1，1)模型对东北地区铁路货运量进行预测

4.1 对已知数据建立模型进行预测

根据东北地区2004年至2010年的铁路货运量统计数据［9］建立模型，首先进行已知货运量年份的预测工作，对模型的可行性进行分析。

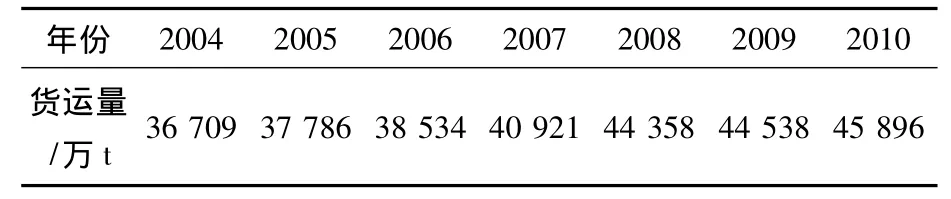
表3 2004—2010年东北地区铁路货运量原始数据表Table 3 2004—2010 Original data of northeast railway freight volume

原始数据序列为:x(0)={36 709，37 786，38 534，40 921，44 358，44 538，45 896}

对原始数据叠加一次得:x(1)={36 709，74 495，113 029，153 950，198 308，242 846，288 742}。

根据式(2)和(3)可得:x(1)(k+1)=845 419.6e0.0419(k+1)－ 844 894.55

根据公式(4)可得预测模型为:x^(0)(k+1)=845 419.6［e0.0419(k+1)－ e0.0419k］(5)

将 k=1，2，3，4，5，6 代入上式，得到2005 年至2010年东北地区铁路货运量的预测结果。

采用该模型对2011年铁路货运量进行预测，去掉原始序列x(0)(k)中最老的2004年数据x(0)(1)，加入最新的2011年数据x(0)(8)，组合成新陈代谢GM(1，1)模型的新原始序列x(0)(k')={37 786，38 534，40 921，44 358，44 538，45 896，47 130}，重复上面的建模步骤进行预测，得到2006—2011年的铁路货运量的预测结果见表4。

4.2 对预测数据进行精度检验

表4 2006－2011年东北地区铁路货运量预测数据表Table 4 2006－2011 forecast data table of northeast railway freight volume

4.3 对未知数据建立模型进行预测

根据东北地区政府的大力支持和迅猛发展的经济背景，为了得到更接近的预测值采用新陈代谢GM(1，1)模型对2012—2015年的铁路货运量进行预测，预测结果见表5。

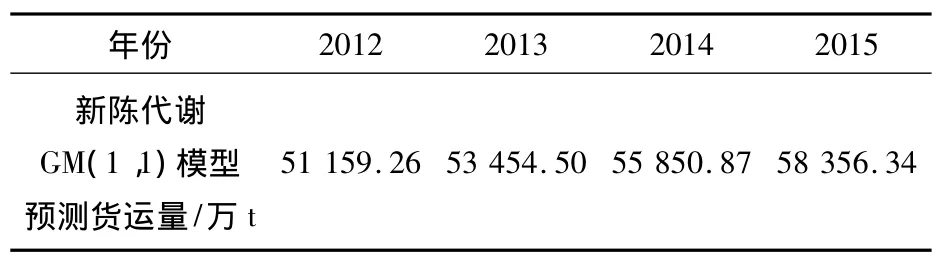
表5 2012－2015年东北地区铁路货运量预测数据表Table 5 2012—2015 forecast data table of northeast railway freight volume

5 结论

灰色GM(1，1)模型预测的本质是一种指数增长预测，成功地建立和应用灰色模型的必要和充分条件是原始数据序列必须是非负的、单调的并符合指数规律［10］。东北地区铁路货运量数据满足新陈代谢灰色模型预测的数据要求，对已知货运量年份的数据预测精度达到一级标准。在全面振兴东北等老工业基地的大趋势下，采用更合理的新陈代谢GM(1，1)模型对未来4年的东北地区铁路货运量进行预测发现:新模型对预测量有着更乐观的结果，符合现阶段东北地区的发展态势。

［1］安树伟，肖金成，吉新峰.“十二五”时期我国区域政策调整研究［J］.发展研究，2010(7):12－15.AN Shu-wei，XIAO Jin-cheng，JI Xin-feng.China’s regional policy adjustment in“Twelfth Five Year”period［J］.Development Research，2010(7):12 －15.

［2］刘思峰，谢乃明.灰色系统理论及其应用［M］.北京:科学出版社，2008.LIU Si-feng，XIE Nai-ming.Grey system theory and its application［M］.Beijing:Science Press，2008.

［3］邓聚龙.灰色预测与决策［M］.武汉:华中科技大学出版社，1988.DENG Ju-long.Grey forecasting and decision［M］.Wuhan:Huazhong University of Science and Technology Press，1988.

［4］吴晓玲，符 卓，王 璇，等.铁路货运量组合预测方法［J］.铁道科学与工程学报，2009，6(5):89 －92.WU Xiao-ling，FU Zhuo，WANGXuan，et al.Combine －forecast method for railway freight volumes［J］.Journal of Railway Science and Engineering，2009，6(5):89 －92.

［5］谭司庭，史 峰.改进的货运量最优变权组合预测模型［J］.铁道科学与工程学报，2011，8(3):104－109.TAN Si-ting，SHI Feng.An improved combined model based on optimal variable weight for prediction of freight volumes［J］.Journal of Railway Science and Engineering，2011，8(3):104 －109.

［6］LIU Si-feng，Jeffrey Forrest.Advances in grey systems of 2007 IEEE international conference on grey systems theory and its and intelli applications［C］//Proceedings Services.Nanjing，2007.

［7］张 军.灰色预测模型的改进及其应用［D］.西安:西安理工大学，2008.ZHANG Jun.Improvement of grey forecasting model and its application［D］.Xi’an:Xi’an University of Technology，2008.

［8］朱大鹏，李严峰，曹 杰，等.基于改进的灰色模型对货物周转量的预测:以云南省货物周转量为例［J］.物流科技，2012(1):1－5.ZHU Da-peng，LIYan-feng，CAOJie，et al.Prediction of freight turnover in Yunnan based on improved grey model［J］.Logistics Sci－Tech，2012(1):1 －5.

［9］中华人民共和国国家统计局.中国统计年鉴2011［R］.北京:中华人民共和国国家统计局，2011.National Bureau of Statistics of China.2011 Yearbook of China Statistical［R］.Beijing:National Bureau of Statistics of China，2011.

［10］张永杰.灰色系统理论在道路货运量、货运周转量预测中的应用［J］.交通运输系统工程与信息，2003，3(1):75－79.ZHANG Yong-jie.Forecast freight quantity and turnover quantity base on grey model theory［J］.Journal of Transportation Systems Engineering and Information Technology，2003，3(1):75 －79.