出口底开门敞车车体振动疲劳分析*

方 吉，兆文忠

(大连交通大学交通运输工程学院，辽宁大连 116028)

由于出口底开门敞车载在他国运行近两个月的时间里，部分车体端部侧墙的焊缝出现开裂现象(见图1)，由于出口国该车的实际应用过程中有振车卸货的特殊工况，这是该车在设计中没有考虑到的，振车器的激振载荷是否是导致侧墙的焊缝开裂的根本原因，针对这一问题展开研究。首先建立底开门敞车车体结构有限元模型，在Nastran软件中进行模态分析，模态结果中有一阶侧墙局部模态的频率与振车器激振频率24 Hz很接近，在此激振频率下车体侧墙局部可能发生共振，为了验证其正确性，利用Nastran软件对其进行简谐激振响应分析，并根据BS标准对侧墙焊缝疲劳寿命进行评估，得出侧墙焊缝疲劳寿命与实际使用2月开始出现裂纹的现象吻合，证明了振车器的激振载荷是导致侧墙的焊缝开裂的根本原因这一结论。对于该车在振车器振车卸货工况下的端部侧墙板的局部共振，提出了几种改进方案，采用时域分析法对该车车体进行振车器振车卸货工况模拟分析，获得用于疲劳寿命预测的动态应力变化范围进行疲劳寿命预测，最终确定能够满足振车卸货工况下疲劳寿命要求的改进方案。

图1 侧墙焊缝开裂的位置Fig.1 The location of the side wall weld cracking

1 原车体结构模态、谐响应及疲劳分析

1.1 有限元模型

车体结构全部采用薄壳单元离散，在振车卸货工况下，车下底门全部打开的状态，底门是以集中质量元的形式固定在相应的连接位置，单元总数为111 928;结点总数为106 890。该车的有限元网格如图2所示。

图2 车体结构的有限元网格Fig.2 Finite element mesh of the car－ body structure

1.2 模态分析

用NASTRAN软件共计算车体50阶模态。观察各个模态振型，发现1个极其重要的模态即第6阶模态(见图3)。该阶模态的固有频率为23.87 Hz。从它的振型位移图中还可以看出:这是1个典型的局部模态，振型为垂直侧板的振动，发生在车体每一个侧墙的两端。这意味着一旦有24 Hz左右的外界激励频率，这2个侧板将一定发生剧烈的共振［1］。

图3 固有频率为23.87 Hz的局部振型Fig.3 Natural frequency for the 23.87 Hz local mode

1.3 谐响应分析

在NASTRAN软件中，根据现场资料，在侧墙上的作用区间长度为2.5 m，可以建立振动器施加到每一侧墙的动态载荷模型:F(t)=3.75×sin(2πft)，求解了振动器工作时的谐响应［2］。结果表明:在24 Hz的激励作用下，固有频率为24.67 Hz的侧墙局部模态产生了较明显的共振。垂直板面的位移最大振动幅值为25.5 mm(图4)。考核焊缝处疲劳强度的最大主应力从+74.9～－74.9 MPa(图5)，以每秒24次规律的交替变化。在车辆工作中，这是一个罕见的、典型的共振现象［2－5］。

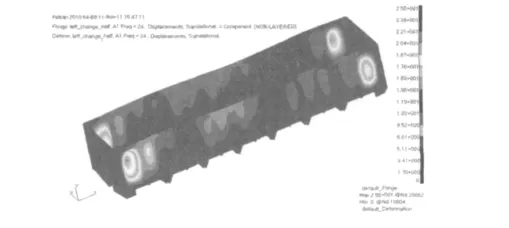
图4 24 Hz激扰下垂直板面的位移云图(最大位移为25.5 mm)Fig.4 Displacement perpendicular to the plate surface under excitation of 24 Hz(the maximum displacement is 25.5 mm)

图5 24 Hz激扰下的应力图(焊缝处最大主应力为74.9 MPa)Fig.5 Stress diagram under excitation of 24 Hz(the maximum principal stress of the weld is 74.9 MPa)

1.4 疲劳寿命预测

该车车体材料为耐侯钢，根据中国铁道部的标准 TB/T 1335—1996［6］中的表3 给出的数据是，该材料(CuPCrNi)的许用应力为184.0 MPa，屈服强度为 294.0 MPa。

在英国标准7608:1993《钢结构疲劳设计与评估》中，寻找到了1个焊接接头几何形状近似、施加载荷也一致的S－N曲线数据，从该标准的表14中确认了疲劳等级(FAT)为F2级，其S－N曲线的常数 C=1.231 ×1 012，斜率 M=3。

假设每天振动卸货1次，每次为4 min，振动频率为24 Hz，于是，每天卸货的振动次数为5 760次。疲劳失效处的最大主应力的变化是从+74.9～ －74.9 MPa 交替变化，变化范围为 149.2 MPa，疲劳寿命的计算公式为:

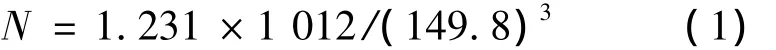
于是，疲劳寿命为N=366 204次，换算为天数，则疲劳寿命为63.6 d，即寿命为2月多。以上计算结果与实际情况基本吻合，因此，证明了由于振车器的以24 Hz的载荷进行振车卸货，引起端部侧墙板的局部模态共振，从而导致该车使用不到2月就出现焊缝列开现象。

2 改进方案分析

修改方案的措施就是在发生问题的部位(即车体侧墙板)通过调整局部刚度以达到避开24 Hz的共振频率。由于端部侧墙板其面积比其他侧墙板要大，其刚度比其他侧墙板薄弱，所以，振动能量的在该位置释放。因此，改进方案首先要加强此处的刚度，在原车体结构在端部侧墙板上下各增加1条厚度为6 mm的钢板，并考虑到端部侧墙板刚度增加，振动能量可能会转移到其他侧墙板位置进行释放，因此，其他侧墙板的刚度也需要适当的增加，特在两边侧墙板中间位置添加如图6所示的角钢。

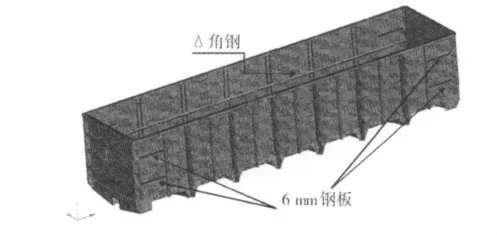
图6 改进方案Fig.6 Improved program

2.1 模态分析对比

通过改进方案的模态计算并与原结构的模态计算结果列入表1中，通过对比可以看出:改进方案消除了24 Hz附近的侧墙局部模态，取而代之的是一些整体模态，且离24 Hz激振频率都较远。因此，在24 Hz下不会出现较强共振现象。

表1 改进方案与原结构在24 Hz附近的模态对比Table 1 Modals near 24 Hz of Improved program and the original structure

2.2 时域响应计算及疲劳寿命预测

由于载荷频率较高，且模型节点自由度比较多，因此，为了提高计算效率，采用模态叠加法计算时域响应［7－10］。实际振车器的位置是不固定的，哪些部位有未卸载完的货物就在未卸载完的货物上方激振，因此，从中抽象出端部加载和中部加载两种情况进行计算。载荷和频率与实际情况保持一致，见图7。考虑结构自身重力，考虑转向架摇枕弹簧的缓冲作用，在心盘处施加摇枕弹簧约束。提取关键焊缝(见图8～11)的最大主应力的变化范围，从BS标准中选择对应焊接接头类型的S－N曲线进行疲劳寿命预测，见表2。在评估疲劳寿命时，假定激振器每天工作4 min，因激振频率为24 Hz，所以，假定每天振动次数为5 760次，同时并假定每年工作365 d，这样就可以将寿命(次数)折算为以年为单位的评估结果，该结果见表2和表3。

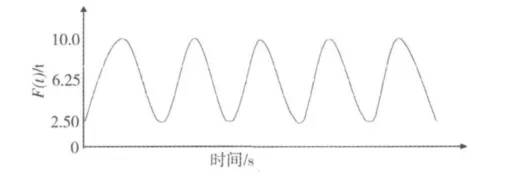
图7 动态载荷示意Fig.7 Dynamic load indication

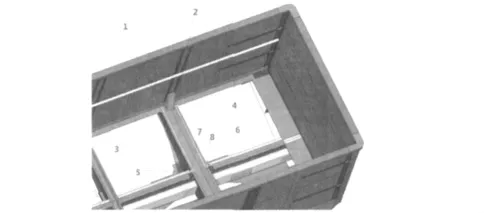
图8 枕梁处焊缝位置Fig.8 The weld line at Corbel

图9 边梁处焊缝位置Fig.9 The weld line at edge beam

通过表2和表3的计算结构可以看出:中部加载情况下关键焊缝的疲劳寿命都满足28 a的设计使用寿命，但端部加载情况下存在唯一的1条焊缝(第16条)疲劳寿命没达到设计要求。因此，需要对该处进行局部再改进。

图10 端部侧墙处焊缝位置Fig.10 The weld line at the end of the side wall

图11 中部侧墙处焊缝位置Fig.11 Weld line at the middle of the side wall

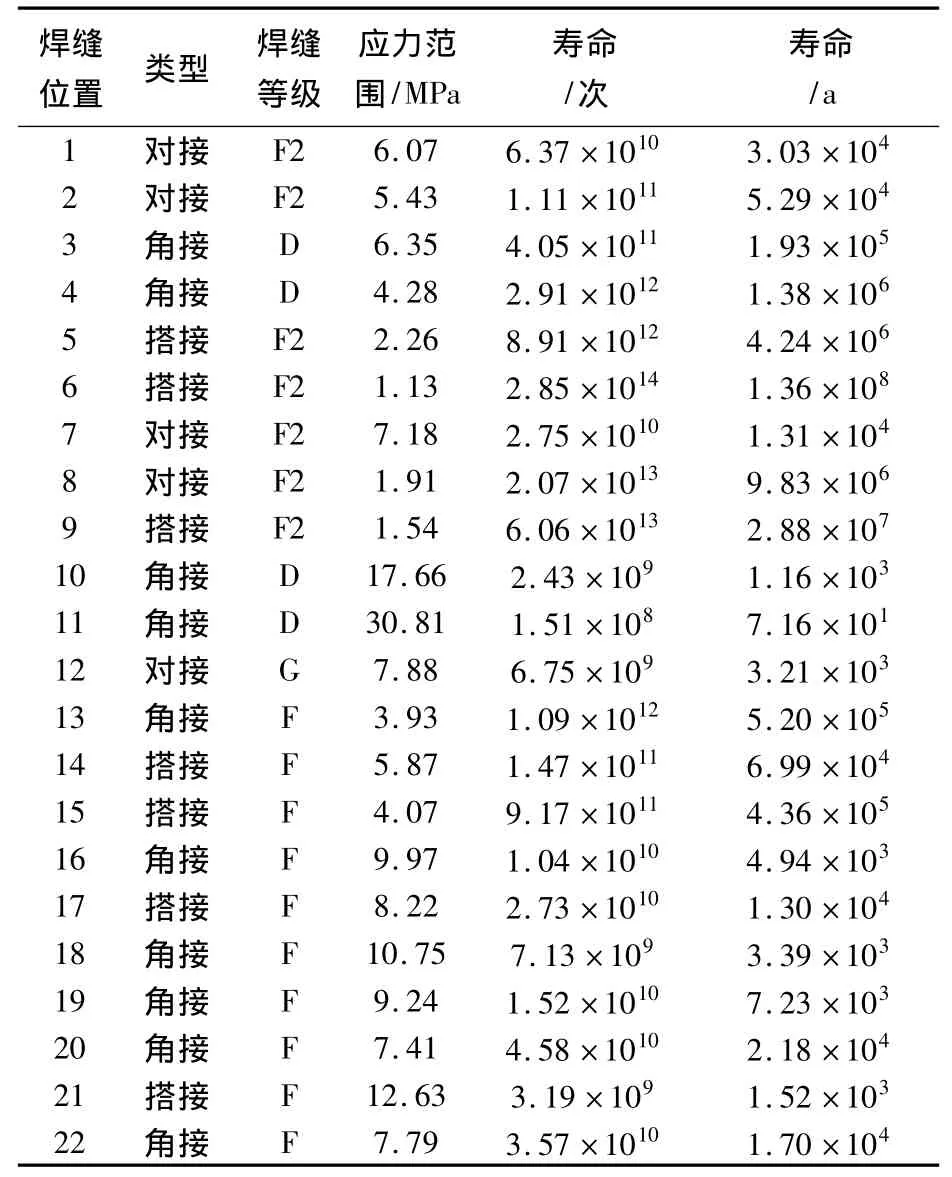
表2 中部加载车体结构关键焊缝疲劳寿命Table 2 Fatigue life of key weld lines in car－body under mid excitation

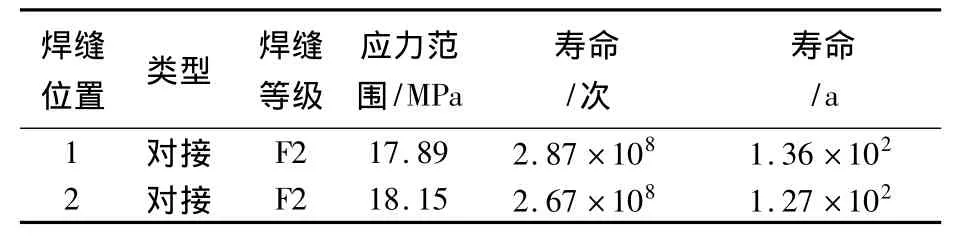
表3 端部加载车体结构关键焊缝疲劳寿命Table 3 Fatigue life of key weld lines in car－body under end excitation

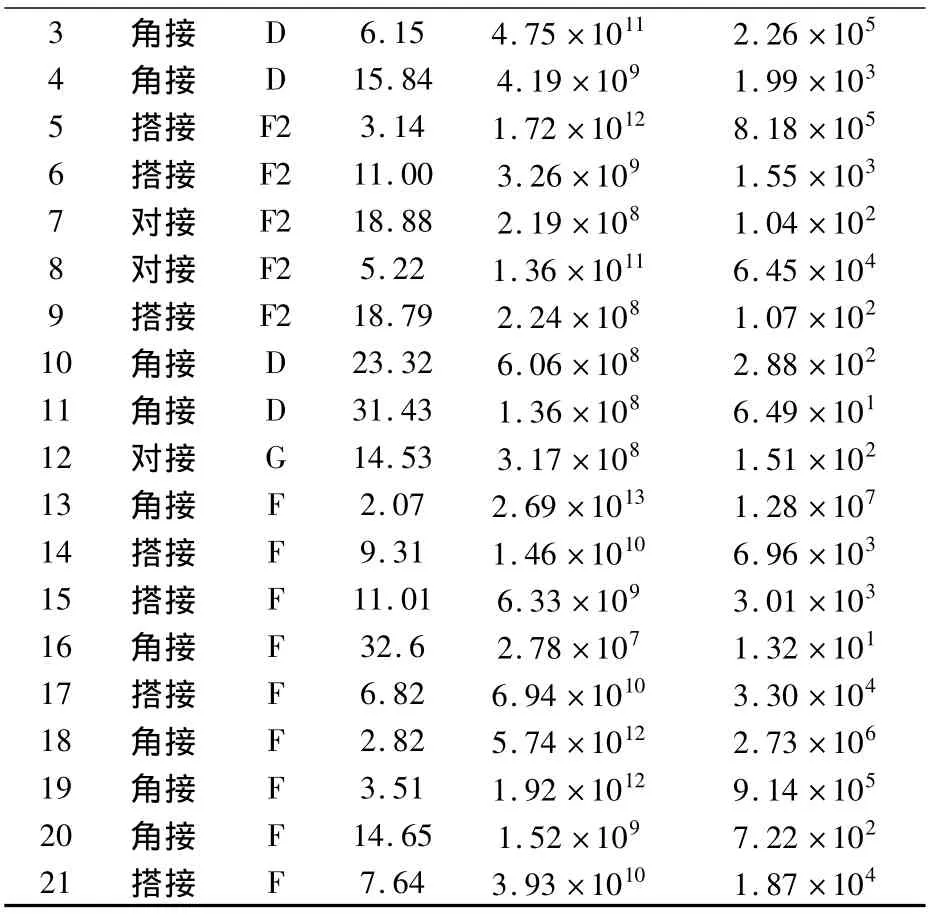
3 角接 D 6.15 4.75×1011 2.26×105 4 角接 D 15.84 4.19×109 1.99×103 5 搭接 F2 3.14 1.72×1012 8.18×105 6 搭接 F2 11.00 3.26×109 1.55×103 7 对接 F2 18.88 2.19×108 1.04×102 8 对接 F2 5.22 1.36×1011 6.45×104 9 搭接 F2 18.79 2.24×108 1.07×102 10 角接 D 23.32 6.06×108 2.88×102 11 角接 D 31.43 1.36×108 6.49×101 12 对接 G 14.53 3.17×108 1.51×102 13 角接 F 2.07 2.69×1013 1.28×107 14 搭接 F 9.31 1.46×1010 6.96×103 15 搭接 F 11.01 6.33×109 3.01×103 16 角接 F 32.6 2.78×107 1.32×101 17 搭接 F 6.82 6.94×1010 3.30×104 18 角接 F 2.82 5.74×1012 2.73×106 19 角接 F 3.51 1.92×1012 9.14×105 20 角接 F 14.65 1.52×109 7.22×102 21 搭接 F 7.64 3.93×1010 1.87×104

3 局部再改进方案分析

由于第16条焊缝是连接侧墙小立柱与侧墙上边梁的焊接结构，载荷从上边边梁往下传力过程中，由于该处的刚好在传力路径上且刚度不协调从而导致应力集中，因此，其疲劳寿命下降，局部再改进方法主要围绕协调该处刚度为目的展开，共设计如下3种方案见图12～14，其焊缝疲劳寿命预测见表4。

图12 局部改进方案一Fig.12 Local improvement program 1

图13 局部改进方案二Fig.13 Local improvement program 2

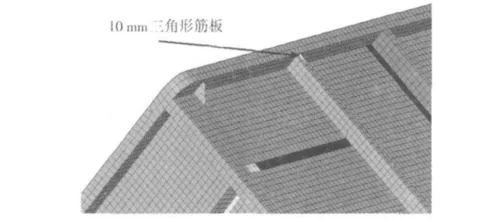
图14 局部改进方案三Fig.14 Local improvement program 3

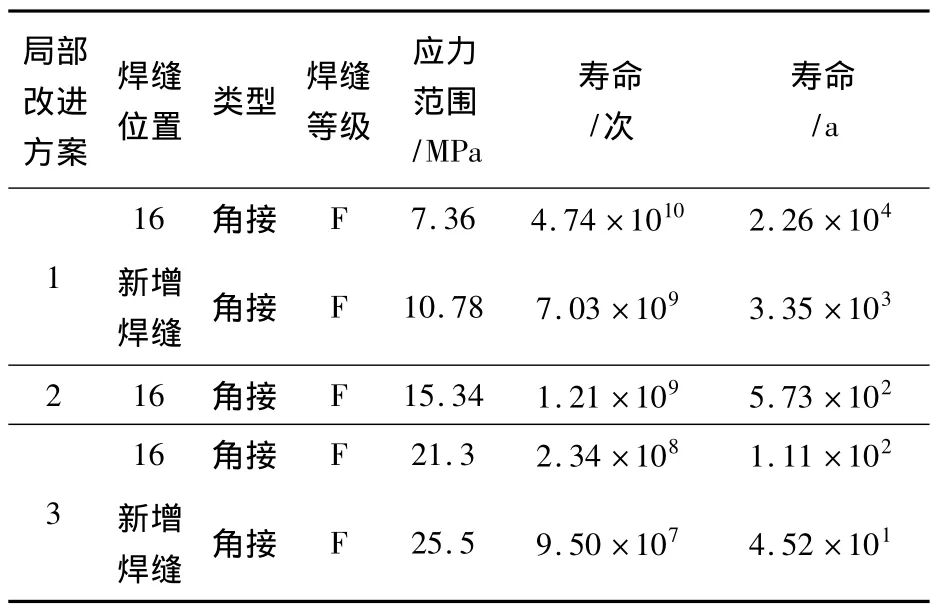
表4 局部改进方案疲劳寿命预测Table 4 Fatigue life prediction of local improvement programs

4 结论

(1)通过振动器振车卸货工况下的模态及简谐响应分析，得出侧墙板的局部共振是引起侧墙板与立柱连接处焊缝开裂的主要原因。

(2)通过改进方案模态分析及关键焊缝疲劳寿命计算，可以看出改进方案已经很好地消除了局部共振，有效地提高了车体侧墙焊缝的疲劳寿命，但还有个别焊缝疲劳寿命未达到28 a设计寿命标准。

(3)通过3种局部再改方案的计算，使第16条焊缝的疲劳寿命得到很大提升，其寿命都超过了28 a的设计寿命要求，且添加筋板结构带来的新焊缝疲劳寿命也满足设计要求。具体应该采用哪种局部改进方案还要根据实际条件和工艺难易程度等因素来决定。

［1］盛宏玉.结构动力学［M］.合肥:合肥工业大学出版社，2005.SHENG Hong-yu.Structural dynamics［M］.Hefei:Hefei University Press，2005.

［2］张 林，高翠琢，吴景峰.基于大质量法的谐响应有限元分析［J］.半导体技术，2011(5):402－405.ZHANG Lin，GAO Cui-zhuo，Wu Jing-feng.Harmonic finite element analysis based on large mass method［J］.Semiconductor Technology，2011(5):402 －405.

［3］康 熊，曾宇清.车辆振动加速度响应分析的速度—频域方法［J］.中国铁道科学，2012(1):60－70.KANG Xiong，ZENG Yu-qing.Speed－frequency domain method for the response analysis of vehicle vibration acceleration［J］.China Railway Science，2012(1):60 －70.

［4］牛恩拂，张玉增，柴 山.基于谐响应方法的某载货车振动分析［J］.农业装备与车辆工程，2012(5):8－11.NIU En-fu，ZHANG Yu-zeng，CHAI Shan.Analysis of a certain truck s vibration based on the method of harmonic response［J］.Agricultural Equipment＆ Vehicle Engineering，2012(5):8 －11.

［5］柴 山，吕凤军，孙义冈，等.计算汽轮机叶片动应力的谐响应分析法［J］.汽轮机技术，2002(5):267－281.CHAI Shan，LUFeng-jun，SUN Yi-gang，et al.Computation for dynamic stress of steam turbine blade by using the method of harmonic response analysis［J］.Turbine Technology，2002(5):267 －281.

［6］英国标准7608:1993钢结构疲劳设计与评估［S］.British Standard 7608:1993，steel fatigue design and evaluation［S］.

［7］顾家柳，任兴民.结构瞬态响应数值积分法的稳定性［J］.振动工程学报，1991(1):79－83.GU Jia-liu，REN Xing-min.Stability of numerical integration method for calculation of transient dynamic responses of structures［J］.Journal of Vibration Engineering，1991(1):79－83.

［8］张 健，金学松，肖新标，等.车辆－轨道耦合动力学钢轨模型求解方法［J］.交通运输工程学报，2011(2):33－38.ZHANG Jian，JIN Xue-song，XIAO Xin-biao，et al.Solution methods of rail model in vehicle－track coupling dynamics［J］.Journal of Traffic and Transportation Engineering，2011(2):33 －38.

［9］张 勇，陈 宝，欧 健，等.整车刚柔耦合动力学模型及平顺性优化［J］.西南师范大学学报:自然科学版，2012(5):68－37.ZHANG Yong，CHEN Bao，OU Jian，et al.Vehicle rigid－flexible coupling dynamics model and ride comfort optimization［J］.Journal of Southwest China Normal University:Natural Science Edition，2012(5):68 －37.

［10］姜雪娇，齐双强，齐双峰，等.基于刚－柔耦合模型的C80B型敞车动力学性能研究［J］.起重运输机械，2012(5):25－28.JIANG Xue-jiao，QI Shuang-qiang，QI Shuang-feng，et al.Dynamics performance research on C80B gondola car based on rigid － flexible coupling model［J］.Hoisting and Conveying Machinery，2012(5):25 －28.