一类驼峰调车事故的贝叶斯网络模型研究*

张春民，李引珍，何瑞春

(兰州交通大学交通运输学院，甘肃兰州 730070)

驼峰进行调车作业时，在车辆自由溜放的过程中，若前行车的速度较慢，而后行车的速度快，在进入道岔地段时有可能出现这样2种状况［1］:一是道岔来不及转换，后行车与前行车连挂撞车，进入了同一股道，导致跟钩撞车;二是道岔可以转换，但前行车还没有到达调车场线路内警冲标时，后行车就进入了相邻股道，导致侧面冲突。跟钩撞车及侧面冲突是对驼峰作业安全影响最大的调车事故之一［1］。这类调车事故的发生会使得驼峰解体作业被迫停止，不仅影响调车作业的安全，还影响驼峰的解体效率。驼峰是包含很多设备的复杂性大系统，工作环境多变，导致该类调车事故发生的因素涉及到线路，调速设备，车辆，天气等方面，有多种可能性导致该类事故的发生，影响因素之间的关系具有不确定性，较难判断其因果关系。一些常用来分析事故的方法如定性分析方法［1－7］、定量分析法如事故树、故障树等存在无法反映基本事件对事故发生影响程度或者难以描述影响因素之间不确定性关系的问题。而近十几年来发展起来的贝叶斯网络技术是将图论和概率论相结合的一种方法，与事故树、故障树有一定的相似性，具有描述非确定性逻辑关系的能力，可以很好地解决不确定性问题［8］，为此，采用贝叶斯网络进行该类调车事故分析。

1 影响因素分析

影响驼峰跟钩撞车及侧面冲突调车事故的因素有多方面，从驼峰技术条件的角度考虑主要有以下3个方面:车辆情况，线路设计情况和调速设备情况。

1.1 车辆情况(Y3)

车辆因素主要有车辆推峰速度以及车辆组合2个方面。

(1)最不利车辆组合。难行车所受的溜放阻力最大，但车辆重量最小，在溜放过程中容易减速，而易行车或新型重载车溜放阻力小，但车辆质量大，易加速。因而最不利的车辆组合是前钩车为难行车，而后钩车为易行车或者是新型重载车。

(2)推峰速度。推峰速度直接影响着车辆的溜放速度和车辆溜放间隔。当车辆组合为最不利组合时，易行车的推峰速度是否合适会增加此类事故的发生。

1.2 线路情况(Y1)

(1)平面设计情况。平面影响因素主要涉及2个方面:一方面是峰顶到第一分路道岔的距离。该段线路位于驼峰溜放部分纵断面上加速坡范围内而且不设调速设备，车辆在这段坡段上速度会迅速增加，影响在后面溜放部分内车辆速度的控制。另一方面是溜放钩车共同走行径路的长度，即从峰顶到调车场警冲标处。

(2)纵断面设计情况。在传统驼峰纵断面设计理论中，驼峰纵断面是兼顾难行车和易行车而设计。当以难行车为依据设计坡度和坡长时，易行车的速度会增大。当以易行车为依据设计坡度时，难行车速度会减小，即每个坡段纵断面依据某一种计算车辆进行设计时，其他类型车辆的速度均会有影响。

1.3 调速设备情况(Y3)

溜放部分的减速器是影响该类事故发生的主要设备，包括2个方面:一方面是减速器提供的制动力大小。另一方面是减速器对车辆速度的精确控制。

另外，自然气候会对车辆、线路以及调速设备产生影响，在恶劣气候条件下，车辆性能、调速设备等的性能均会发生变化，增加事故发生的可能性，因此，这里将其看作基本事件。

2 贝叶斯网络模型的建立

贝叶斯网络是一个有向无环图，可以形式化的表示为 B(G，p)［9］。G=(V，E)表示贝叶斯网络图是一个有向无环图，其中，V={v1，v2，…，vN}是网络中的节点集合。E是各节点之间的有向边，表示彼此之间的因果关系，对于有向边E=(vi，vj)，表示为vi是vj的父节点，vj是vi的子节点。p是与每个节点相关的条件概率分布，定量描述节点之间的概率关系。

2.1 事故树向贝叶斯网络的转化

为便于建立贝叶斯网络模型，并能充分运用历史信息，在本文的方法中，首先建立三方面影响因素的事故树，然后进行整合和修正，得到贝叶斯网络模型，进而利用所建立的贝叶斯网络模型进行跟钩撞车及侧面冲突调车事故的分析。

事故树中的与门、或门、条件与门，条件或门等逻辑门符号所对应的贝叶斯网络以及条件概率见图1［10］。其中，0表示事故不发生，1表示事故发生。

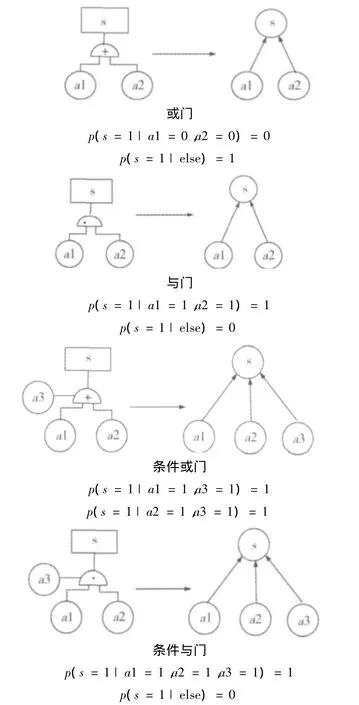
图1 事故树逻辑关系的贝叶斯网络表示Fig.1 Description of fault tree logical relation by Bayesian network

2.2 建立事故树

依据1中对3个方面影响因素的分析，建立各自的事故树，如图2所示，图中符号说明见表1。

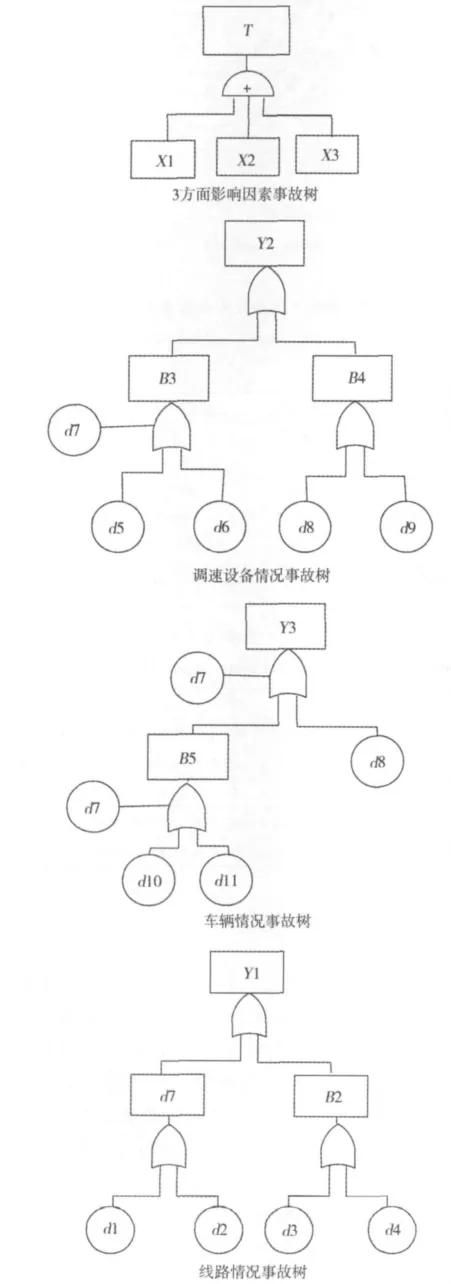
图2 影响因素的事故树Fig.2 Fault trees of factor

表1 事故树符号说明表Table 1 Description of fault tree symbols

2.3 建立贝叶斯网络模型

将上述建立的事故树转化成各自相应的贝叶斯网，并进一步得到系统的贝叶斯网络模型以及所对应的条件概率，如图3和图4所示。

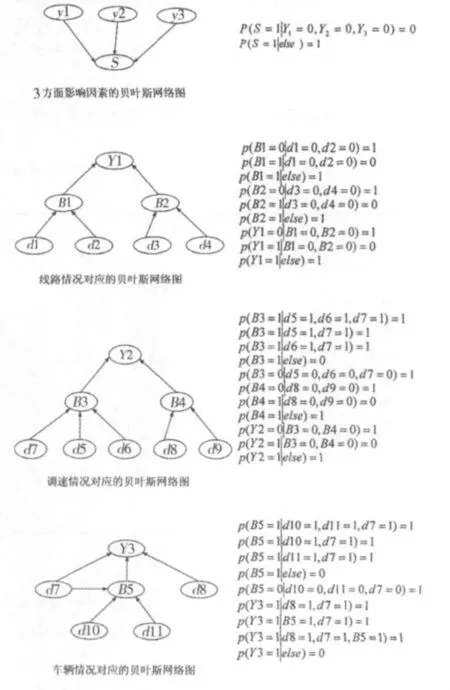
图3 事故影响因素对应的贝叶斯网络图Fig.3 Corresponding Bayesian network of factors

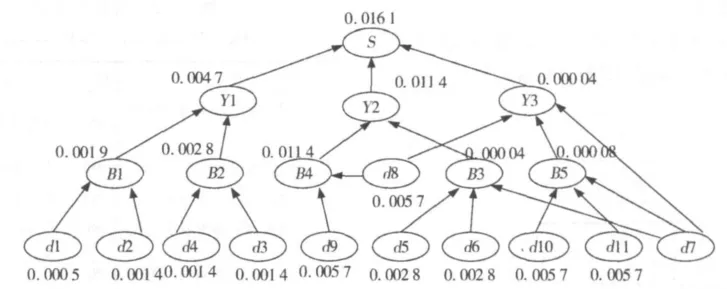
图4 溜放车辆跟钩撞车，侧面冲突事故的贝叶斯网络模型Fig.4 Bayesian network of the rolling car rear－ end and side collision condition

3 贝叶斯网络模型推理与分析

3.1 推理计算

为便于推理计算，采用文献［1－7，10］对实际案例的分析来确定每个基本事件对事故的影响次数，并确定出各基本事件发生的先验概率，见表2和表3。其中，表2中有些影响因素如d1没有反应其发生的次数，考虑现场实际情况来确定其发生的先验概率。

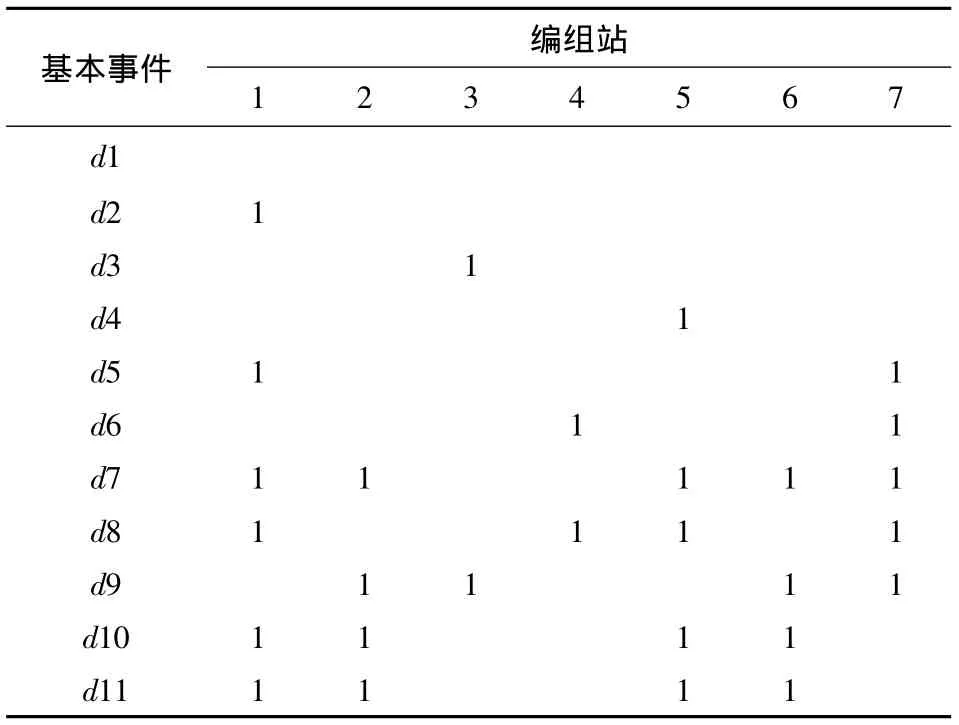
表2 部分编组站追钩撞车、侧面冲撞调车事故案例数据分析表Table 2 Data of the rear－end and side collision condition at some marshalling stations

根据表3中先验概率，运用matlab中的BN推理工具软件包BNT计算所建贝叶斯网络模型中各节点的边缘概率和后验概率。各节点的先验概率以及计算所得后验概率如表4所示，计算所得各节点的边缘概率以及顶上事件的发生概率如图4所示。

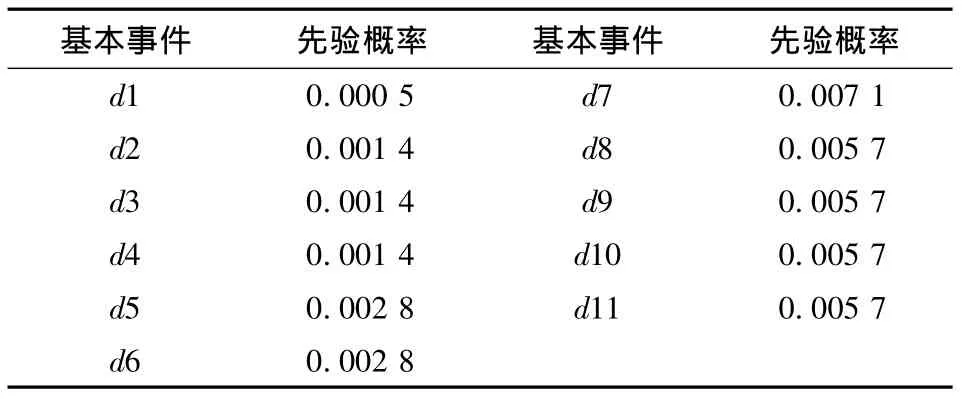
表3 追钩撞车、侧面冲撞事故影响因素先验概率表Table 3 Probability of the rear－end and side collision condition factors

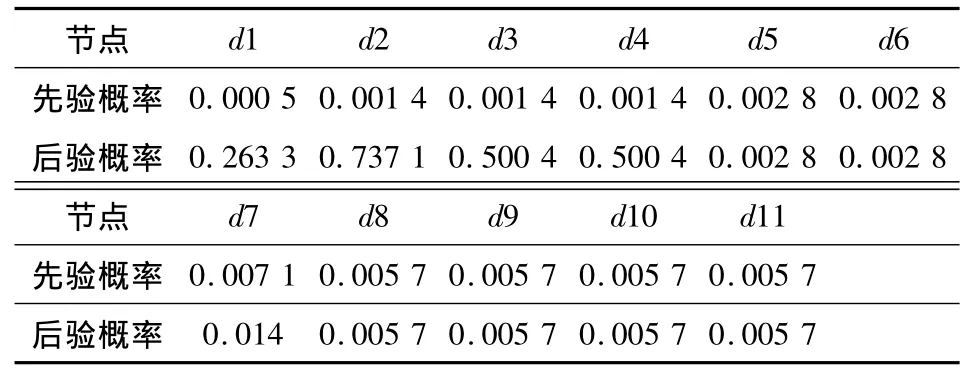
表4 各根节点的先验概率和后验概率Table 4 Prior probability and posterior probability of each node

3.2 计算结果分析

3.2.1 后验概率分析

从表4可以看出，基本事件d1，d2，d3，d4和d7的后验概率分别为 0.263 3，0.737 1，0.500 4，0.500 4和0.014，较先验概率均有所增加，后验概率是运用贝叶斯网络的推理原理对先验概率进行重新修正得到的计算，可以更为精确地反映事故发生状况。计算结果表明:当该类事故发生时，这些基本事件的发生概率较大，成为主要的影响因素。

3.2.2 基本事件的影响分析

追钩、侧面冲撞调车事故的主要影响因素按其后验概率从大到小依次是:d2，即咽喉共同径路长，后验概率为0.737 1;d3和d4，分别为纵断面设计不合理和纵断面使用中发生变化，后验概率均为0.500 4;d1，即第一分路道岔设置位置不合理，后验概率为0.2633;d7，为最不利车辆组合，后验概率为0.014。这些影响因素中，d7属于车辆方面，d2，d1，d3和d4属于线路方面，其中，d2和d1为线路平面因素，是该事故发生的最主要影响因素，d3和d4为线路纵断面因素。可见该事故的主要因素集中在线路设计方面和车辆方面，而调速设备对该事故发生的影响程度并不大。

3.2.3 措施方案

从以上分析可知，在实际工作中需考虑2个方面的情况:一是线路设计方面，包括线路平面设计和纵断面设计，尤其是平面设计中车辆共同走行径路长度和第一分路道岔的位置设计要合理。纵断面设计主要是溜放部分各坡段的坡长和坡度要保证前后溜放车辆必要的间隔。另一方面是驼峰运营方面:首先，注意在溜放过程中出现的车辆不利组合情况，可以采取调整后行车推峰速度等办法来控制车辆溜放速度;其次，在使用中要监测线路纵断面的变化。

4 结论

驼峰跟钩撞车，侧面冲突调车事故会给驼峰调车作业带来较大安全隐患，影响驼峰作业的效率和能力。本文在传统驼峰设计理论的基础上，重点研究了驼峰设计技术条件对该调车事故的影响因素，运用贝叶斯网络技术，建立该类调车事故的贝叶斯网络模型，利用Matlab中的BN推理工具软件包BNT进行推理，求得顶上事件的发生概率，各节点的边缘概率以及基本事件的后验概率。结论表明:影响该类调车事故的主要因素集中在线路和车辆方面，在驼峰实际设计和运用中对这2个方面应给于重点考虑。

［1］杜旭升，凌 熙，沈 鹏，等.我国驼峰作业安全情况及调速设备配置的探讨［J］.减速顶与调速系统，2007(4):1－7.DU Xu-sheng，XING Xi，SHEN Peng，et al.Safety status of hump operation and placement of speed control equipments［J］.Retarders and Speed Control Technology，2007(4):1－7.

［2］虞桂海.提高驼峰空车解体作业效率的思考［J］.铁道运输与经济，2003，3(25):34 －40.YU Gui-hai.Thinking on improving break－up operation efficiency of the empty car on hump［J］.Railway Transport and Economy，2003，3(25):34 －40.

［3］李少龙.驼峰作业安全与效率关系的探索与实践［J］.上海铁道科技，2004(6):13－14.LI Shao-long.Exploration and practice of the relationship between safety and efficiency on hump［J］.Shanghai Railway Technology，2004(6):13 －14.

［4］张 志.包头西站驼峰调车作业安全的思考［J］.铁道货运，2012(1):14－18.ZHANG Zhi.Thinking on breaking － up safety in Baotou west marshalling station［J］.Railway Freight Transport，2012(1):14－18.

［5］王以哲.沈阳南站上行编组场溜放车组撞车原因分析及对策［J］.铁道技术监督，2008(5):13 －14.WANG Yi-zhe.the Cause analysis and countermeasures of car－crash accidents in up direction yard of Shenyang south marshalling station［J］.Railway Quality Control，2008(5):13－14.

［6］谢芝林，谭其敏.加强设备维护管理减少编组站驼峰撞车事故［C］//2004年自动化驼峰研讨会论文集，2004:218－220.XIE Zhi-lin，TAN Qi-min.Reduction of car－ crash accidents on hump in Marshalling Station by Strengthening E-quipment Maintenance Management［C］//Symposium on Automation Hump.2004:218 －220.

［7］胡 敏.向塘西编组站设备性能比较及运营分析［J］.铁道运输与经济，2006，28(4):52 －53.HU Min.Operation analysis and performance comparison of equipments in the Xiangtang West Marshalling Station［J］.Railway Transport and Economy，2006，28(4):52 －53.

［8］周忠宝，周经伦，金 光，等.基于贝叶斯网络的概率安全评估方法研究［J］.系统工程学报，2006，21(6):636－667.ZHOU Zhong-bao，ZHOU Jing-lun，JIN Guang，et al.Probabilistic safety assessment research based on Bayesian networks［J］.Journal of Systems Engineering，2006，21(6):636－667.

［9］李典庆，鄢丽丽，邵东国.基于贝叶斯网络的土石坝可靠性分析［J］.武汉大学学报:工学版，2007，40(6):24－29.LI Dian-qing ，YAN Li-li，SHAODong-guo.Reliability evaluation of earth － rock dams using bayesian network［J］.Engineering Journal of Wuhan University，2007，40(6):24－29.

［10］张春民.自动化驼峰纵断面优化设计研究［D］.兰州:兰州交通大学，2011.ZHANG Chun-min.Optimization of vertical section design for atomated hump［D］.Lanzhou:Lanzhou Jiaotong University，2011.