铁路既有线复测平面曲线优化方法*

陈 峰，辜良瑶，杨 岳，吴湘华

(1.中南大学交通运输工程学院，湖南长沙 410075;2.中南林业科技大学机电工程学院，湖南长沙 410004)

既有铁路的线路参数是铁路工务部门进行轨道检测与维保的基准。铁路线路经过运营与维修保养后，其线路参数发生改变，因此需要对线路进行复测，根据复测数据，对线路参数进行优化［1］。根据优化后的线路参数计算线路横、纵段面调整量，可以用于指导大机维修施工。目前，工务管理部门均成立了专业的测量队伍，使用全站仪对铁路既有线复测，获得了高精度的连续线路大地坐标。如何利用高精度的线路大地坐标数据，通过合理的优化计算方法对线路平面曲线参数进行优化调整就成为一项十分重要的工作。对于线路平面曲线复测优化计算方法，文献［2］提出基于方向加速法的平面重构算法，该算法未实现缓和曲线段的调整量计算，重构出的曲线参数不能进行人工干预，得到的曲线优化参数过于精确，无法适应现场的生产管理。如为了测设、施工和养护的方便，平面曲线半径一般取50 m和100 m的整数倍［3］;文献［4］提出采用基于圆曲线最小二乘拟合方法的平面曲线优化方法，在弧径比较小的情况下，圆曲线最小二乘拟合算法无法拟合出合理的圆曲线参数，因而在进行大曲线半径平面曲线优化时，该方法容易产生病态优化结果。为了解决上述问题，本文根据平面曲线几何要素计算原理，提出了基于夹直线最小二乘拟合的平面曲线优化方法。

1 平面曲线特征分界点的判别

线路平面曲线由前夹直线、前缓和曲线、圆曲线、后缓和曲线和后夹直线5个线形要素组成［2］，分别用直缓(ZH)、缓圆(HY)、圆缓(YH)、缓直(HZ)4个特征点进行分界。既有线复测后，平面曲线优化的首要步骤是对被测曲线的4个特征分界点的点位进行判别。

文献［4］根据测量数据进行正矢计算，由正矢的变化规律进行HY和YH分界点的判别。图1所示为一段测量线路的超高和20 m正矢图。从图1可以看出:由于测量误差的影响，正矢是波动值，很难根据正矢值判别特征分界点，而且分界点的选择偏差对圆曲线最小二乘拟合结果敏感度较高。

线路的超高值可以直接从测量中获取，不需要进行换算，能较为直观的区分出平面曲线各特征段，分界点的选择偏差对夹直线最小二乘拟合结果敏感度较低，因此线路的测量超高更适用于特征分界点的判别。

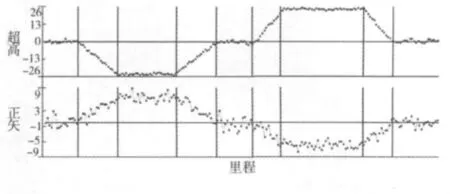
图1 测量线路超高和正矢图Fig.1 Superel evation and versine of measured railway line

2 基于最小二乘的圆曲线拟合方法

在判断出既有线圆曲线、缓和曲线的特征分界点后，即可选取圆曲线上的测点进行拟合。根据最小二乘原理来逼近圆曲线的圆心与半径［4－6］。圆曲线上各测点的残差平方和为:

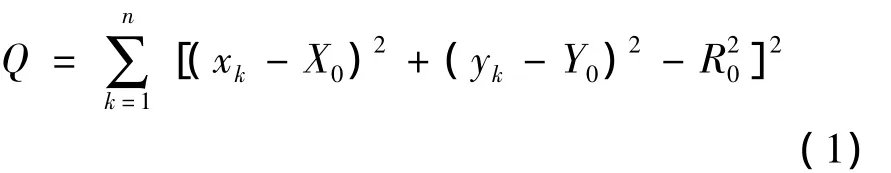
式中:R0为拟合圆半径;(X0，Y0)为拟合圆圆心坐标;(xk，yk)为圆曲线上测点Ck坐标。根据最小二乘原理建立圆曲线拟合半径与圆心坐标计算方程:

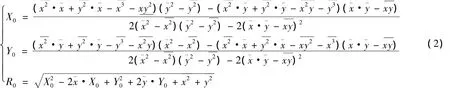
在弧径比L/R很小情况下，使用最小二乘拟合得到的圆心与半径可能会得到一病态值，以下进行分析。

以圆心在(0，0)的标准圆(R=0.5)为例，取4点(0.09，0.49)，(0.28，0.41)，(0.37，0.34)和(0.49，0.1)，弧长 L 约为0.6，采用以上算法拟合得到的圆心为(0.01，0.01)、半径为 0.485，如图2 左图所示。拟合圆与标准圆基本重合，拟合结果较为合理。

在标准圆附近另取 4个相近点(0.360 9，0.346)，(0.360 3，0.346 7)，(0.362 2，0.344 7)和(0.362 8，0.344)，弧 长 L=0.0133，L/R =0.026 6。采用以上算法得到的拟合结果:圆心为(0.361 5，0.345 3)，半径为0.690 7。得到的拟合结果如图2右图所示，拟合圆与标准圆产生了较大差距，拟合结果不合理。

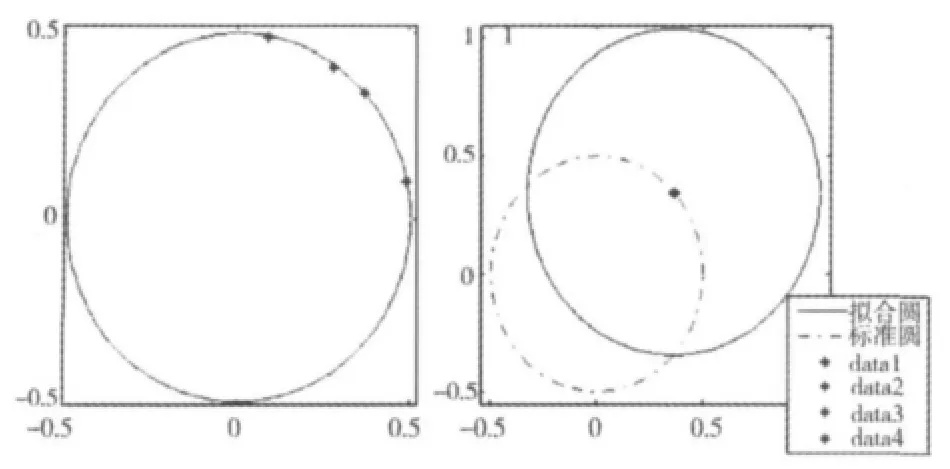
图2 圆曲线拟合病态结果Fig.2 Illness result of circle curve fitting

究其原因，若弧径比过小，则测量点上的微小测量误差，将对圆心的拟合坐标产生较大影响，从而导致拟合结果与实际相差巨大。

在提速线路中大量使用了大半径平面曲线，假设圆曲线长为150 m，曲线半径超过6 000 m的平面曲线，其弧径比即小于0.025，使用圆曲线最小二乘拟合，就有可能导致病态的拟合结果。

相对而言，直线的最小二乘拟合不存在以上问题，而且算法简单。由于平面曲线可由圆曲线半径和前后缓和曲线长3个参数唯一确定，因此，采用最小二乘拟合方法确定前后夹直线后，通过建立平面曲线上各线形要素的调整量计算模型，对圆曲线半径和前后缓和曲线长进行等步长迭代优化计算，计算出平面曲线的最小调整量，即可获得最优的平面曲线参数。

3 基于夹直线最小二乘的平面曲线拟合

3.1 最小二乘的夹直线拟合

夹直线用方程y=Ax+B进行定义，则夹直线上各测点的残差平方和为:

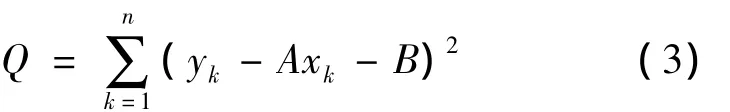
根据最小二乘原理，夹直线的拟合参数为:

采用最小二乘得到拟合参数A和B。夹直线的方位角β=arctan A。从而得到前夹直线方位角β1，后夹直线方位角β2，两夹直线的交点(JD)坐标(xJD，yJD)，以及平面曲线的偏角 α =。因而，直线段上每个测点(xc，yc)的调整量为:

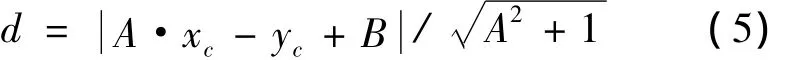
3.2 平面曲线的几何要素

加设缓和曲线的平面曲线(图3所示)的几何要素为:偏角α，曲线半径R，前缓和曲线长l1，后缓和曲线长l2，切线长T，曲线总长L。切线长T和曲线总长L由公式(6)计算:

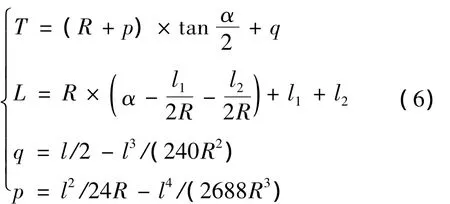
式中:p为内移距;q为切垂距;R，l1和l2为输入参数。

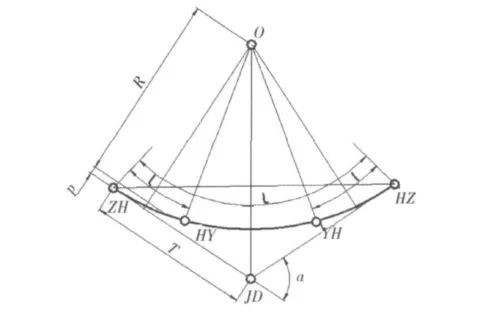
图3 平面曲线Fig.3 Plan curve

3.3 缓和曲线线型计算

在《线规》中明确规定:在不超过160 km/h的客货列车共线运行的铁路，采用三次抛物线作为缓和曲线线型。以前缓和曲线为例，建立以ZH点为原点，切线为X'轴的缓和曲线局部坐标系。可得3次抛物线上各点的计算公式［3］:

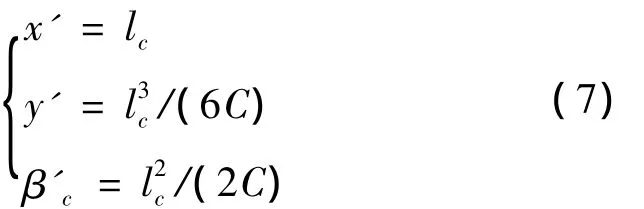
式中:lc为缓和曲线上任一点的弧长;C=R·l1;β'c为该点的缓和曲线角。

由于平面曲线测量是在大地坐标下进行的，需要将局部坐标系转换到大地测量坐标系。若已知ZH点大地坐标和方位角，前缓和曲线上任一点的大地坐标计算公式:

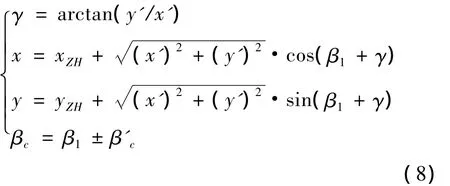
3.4 平面曲线特征点坐标计算

由于ZH和HZ点分别位于始端、终端夹直线上。根据前夹直线方位角β1，得到ZH点的大地坐标为:

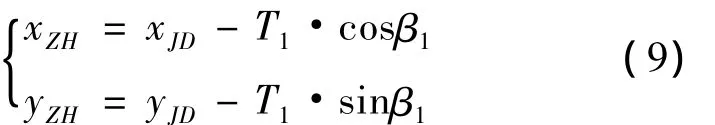
根据后夹直线方位角β2，计算HZ点的大地坐标为:

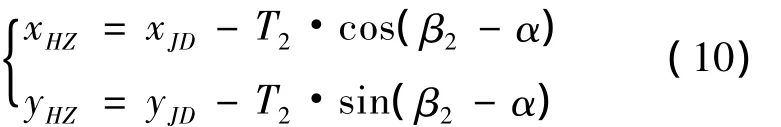
将lc=l1代入式(7)和式(8)即可得到HY点坐标(xHY，yHY)及方位角 βHY。进而计算出圆心坐标:

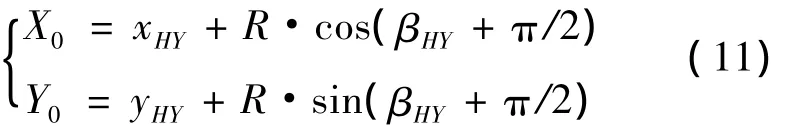
3.5 平面曲线特征点里程计算

将整个平面曲线测量起点设置在夹直线上，将其作为优化曲线的起点，将其测量坐标投影到所在夹直线，得到位于夹直线上的起点坐标(xQD，yQD)，设定该点的里程LQD，可由下式计算出平面曲线特征点的里程:

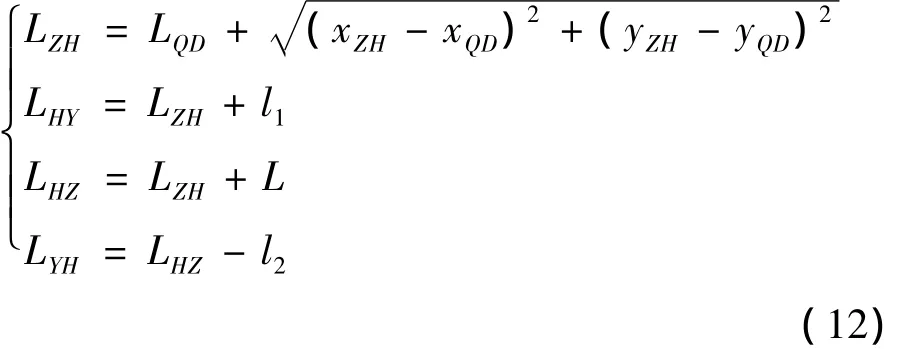
在后续的平面曲线中，前一平面曲线的HZ点为后一平面曲线的起点，前一平面曲线的后夹直线为后一平面曲线的前夹直线。从而计算得到整个测量曲线连续的平面曲线的特征点大地坐标及里程。

4 平面曲线调整量计算

4.1 圆曲线调整量计算

由公式(11)计算得到了圆曲线的圆心坐标，则圆曲线上的调整量即为测量点到圆心的距离减曲线半径:

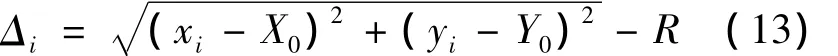
4.2 缓和曲线调整量计算

直线和圆曲线的调整量均能通过几何关系直接算出，在缓和曲线上则比较复杂，本文采用缓和曲线方位角搜索法进行迭代计算［7］。即在缓和曲线上找到法线通过测点的投影点，调整量即为测点与投影点的距离。

取缓和曲线段上的1个测量点C，根据C点与ZH点坐标，先计算ZH→C的方位角θZH→C，若其与ZH点的方位角的夹角＜ 0.01，则 ZH 点即为点的法线里程点。

图4 缓和曲线调整量计算原理图Fig.4 Adjustment calculation of transition curve

否则，计算 c点与ZH 点间距 sZH→c，令li=sZH→c× cosθsZH→c，代入式(7)和(8)，求出 E1 点处的坐标(xE1，yE1)及方位角 βE1。再计算 E1→ c的方位角θE1→c，若其与E1点的方位角的夹角＜0.01，则E1点即为c点的法线里程点。否则重复以上步骤，最后总能找到点En，使En的切线与En－c垂直。

得到En后，则该测量点的调整量为:

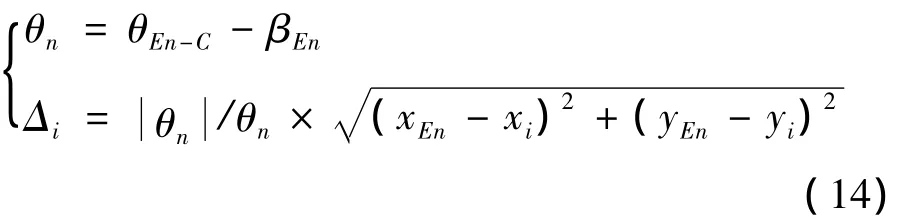
5 平曲曲线优化算法

5.1 算法原理

通过建立的平面曲线调整量计算模型，在两端夹直线不变的前提下，平面曲线的优化问题转换为:以R，l1和l2为优化参数，以调整量最小为优化目标的优化求解问题。建立优化方程:

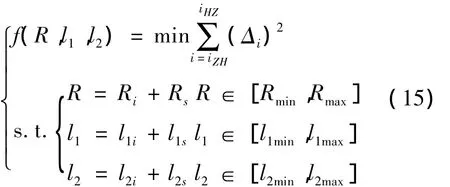
Δi为每个测点的调整量。Rs，l1s和l2s为3个优化参数的迭代步长。前、后夹直线的调整量在进行最小二乘拟合时就已确定，与R，l1和l2无关，因此，只需要对缓和曲线段和圆曲线段进行优化。在线路设计中，平面曲线一般采用对称基本型，即前、后缓和曲线等长，因而还可以减少一个优化参数，提高算法效率。具体的优化步骤如下:

(1)给定R，l1和l2初始值，根据线路养护管理要求设置相应步长(Rs，l1s和 l2s)，根据式(6)，计算始端切线长T1、终端的切线长T2。

(2)根据式(9)和(10)，计算ZH与 HZ点坐标。

(3)将l1代入式(7)和(8)，计算HY点坐标。

(4)将HY点坐标代入式(11)，计算得到圆曲线的圆心坐标。

(5)遍历所有的测点，根据测点坐标值，判断测点所在的特征段。

(6)如果测点位于缓和曲线和圆曲线区域，调用相应的调整量计算模型，计算位于缓和曲线和圆曲线区域的所有测点的调整量。

(7)按照指定步长，调整参数 R，l1和l2。重复以上操作进行最小调整量搜索，直至达到各优化参数的边界条件，计算结束。最小调整量所处的平面曲线参数R，l1和l2即为该平面曲线的最优参数。

5.2 算例

按照上述算法，应用C#语言开发了既有线平面曲线复测优化软件，并对广深I线、广深II线K40～K65试验路段进行了复测。从测量数据中取一段具备前后夹直线的完整既有线为例，对算法进行验证。

算例一:根据工务部门提供的原有曲线参数直接进行平面曲线调整量计算，将计算结果按照测点依次绘制出调整量示意图，如图5(图中上部)所示，图中下部为测量超高。

算例二:设定曲线半径优化范围为6 000～10 000 m，优化步长取100 m，根据现场管理要求缓长保持不变，对测量数据进行优化计算，优化后的圆曲线半径为8 300 m。图6所示为优化后得到的调整量图。

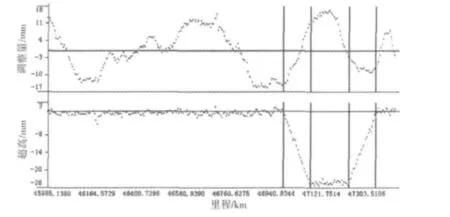
图5 R=8 000调整量图Fig.5 Adjustment when radius is equal to 8 000

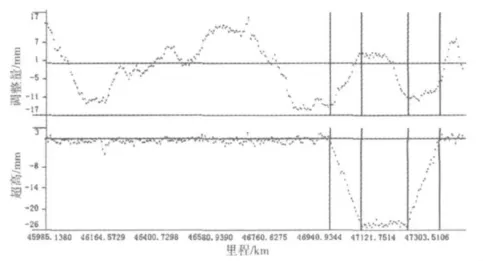
图6 R=8 300调整量图Fig.6 Adjustment when radius is equal to 8 300

从两图中可以看出，优化后的平面曲线，从ZH点到HZ点的调整量明显减少。优化前后的平面曲线参数如表1所示。

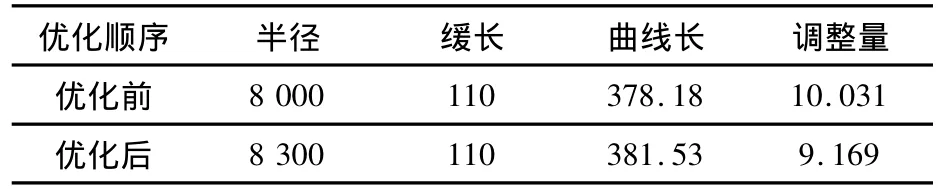
表1 优化结果对比Table 1 Optimization result comparison m

6 结论

(1)基于复测线路的大地测量坐标，建立了基于R，l1和l23个参数的平面曲线特征点大地坐标及里程的计算模型。

(2)采用缓和曲线方位角搜索法，实现了缓和曲线段调整量的计算，从而实现了整个平面曲线任一测点的调整量计算。

(3)根据以上计算模型，提出了基于夹直线最小二乘的平面曲线优化方法，算法简单，易于编程实现。平面曲线优化参数个数、初始值、步长可以根据现场养护需求进行灵活控制。该算法不仅避免了基于圆曲线最小二乘的优化方法出现的病态拟合结果，而且在直线段可加长测点间隔，提高测量效率。

根据广深I线、广深II线K40～K65试验路段的复测数据，采用本文提出的基于夹直线拟合的优化方法，进行了试验区段的平面曲线优化，并根据优化后的参数指导大机精确捣固，捣固后试验路段总体质量逐步提高。广深Ⅰ线捣固后(2011－10－08)质量指数TQI为3.96，比捣固前(7月22日)降低了0.48，广深Ⅱ线质量指数 TQI为3.95，比捣固前降低了 0.61。

［1］李家稳，陈 峰，张海燕，等.坐标法优化拨距计算方法的研究［J］.北方交通大学学报，2004，28(4):34－36.LI Jia-wen，CHEN Feng，ZHANG Hai-yan，et al.Study of the move distance calculation method［J］.Journal of Northern Jiaotong University，2004，28(4):34 －36.

［2］李 伟，蒲 浩，彭先宝.基于方向加速法的铁路既有线平面重构优化算法［J］.铁道科学与工程学报，2009，6(3):47－51.LI Wei，PU Hao，PENGXian-bao.Existing railway plane Line reconstruction algorithm based on direction acceleration method［J］.Journal of Railway Science and Engineering，2009，6(3):47－51.

［3］李远富.线路勘测设计［M］.北京:高等教育出版社，2009.LI Yuan-fu.Route survey and design［M］.Beijing:Higher Education Press，2009.

［4］李红艳，陈治亚，邢 诚，等.铁路既有线曲线复测计算方法［J］.中国铁道科学，2009，30(2):18－22.LI Hong-yan，CHEN Zhi-ya，XING Cheng，et al.Calculation method for curve re－surveying of the existing railway line［J］.China Railway Science，2009，30(2):18 －22.

［5］鲁永辰.坐标法复测既有铁路曲线［J］.铁道勘察，2006，32(3):15 －17.LU Yong-chen.Re－surveying the curves of the existing railways with the method of coordinate［J］.Railway Investigation and Surveying，2006，32(3):15 －17.

［6］王 磊.既有铁路平面改建CAD系统理论与方法的研究［D］.长沙:中南大学土木建筑学院，2008.WANG Lei.Theory and method research on reconstruction CAD system of existing railway［D］.Changsha:School of Civil Engineering，Central South University，2008.

［7］李富强，陈 斐，王 强.已知点坐标换算路线里程的方法及程序［J］.山西交通科技，2005(4):65－67.LI Fu-qiang，CHEN Fei，WANG Qiang.A method and program of using point coordinate to convert route mileage［J］.Shanxi Science ＆ Technology of Communications，2005(4):65－67.