微型抗滑桩组合结构模型试验与结构影响分析*

胡毅夫，王庭勇，唐承铁

(1.中南大学资源与安全工程学院，湖南长沙 410083;2.湖南省高速公路管理局，湖南 长沙 410001)

微型桩自20世纪50年代提出以来，凭借其适应性强，安全性高，施工快，布桩灵活等诸多优势，在工程中得到了广泛的应用［1］。近年来，国内外学者将微型桩应用于滑坡治理、边坡加固、基坑等工程，取得了较好的效果［2－5］。由于微型桩桩径小，单桩抗弯刚度小，所以，微型抗滑桩的应用往往是将多根微型桩按照一定的方式组合起来形成微型桩组合结构，而微型桩组合结构的受力计算目前国内外还鲜有报道［6］。史佩栋等［7］初步讨论了顶梁连接的微型桩承受横向荷载的设计方法，提出了利用“有筋土墙”计算模型。冯君等［8］讨论过顶梁连接的多根微型桩加固顺层岩质边坡的计算方法。吴文平等［9］通过模型试验的位移测试结果将微型桩组合结构简化为平面刚架结构，并将该结构进一步分解为下端为固定支座、上端为滑动支座的均布荷载且上端承受水平集中力的平面刚架结构，但其将荷载均匀分布于各单桩。上述方法均忽略了作为结构体系的微型抗滑桩的结构特性，本文通过模型试验，找到了前后桩的内力分布规律，并在此基础上，利用位移法就结构特性对内力分布的影响进行讨论。

1 试验过程与结果

1.1 试验模型与内容

借鉴Thompson等［10］的研究思路，模型设计为直剪式边坡模型，模型分为滑床和滑体2部分，宽1.2 m，见图1。模型滑体材料由石膏粉和中砂拌合，配合比为M中砂∶M石膏粉=5∶1。滑床材料配合比为 M砂∶M石膏∶M水泥=4∶0.7∶0.3。用涂黄油双层塑料薄膜预设滑面。试验反力墙模型用C30混凝土浇筑。模型边坡坡比为1∶0.75。

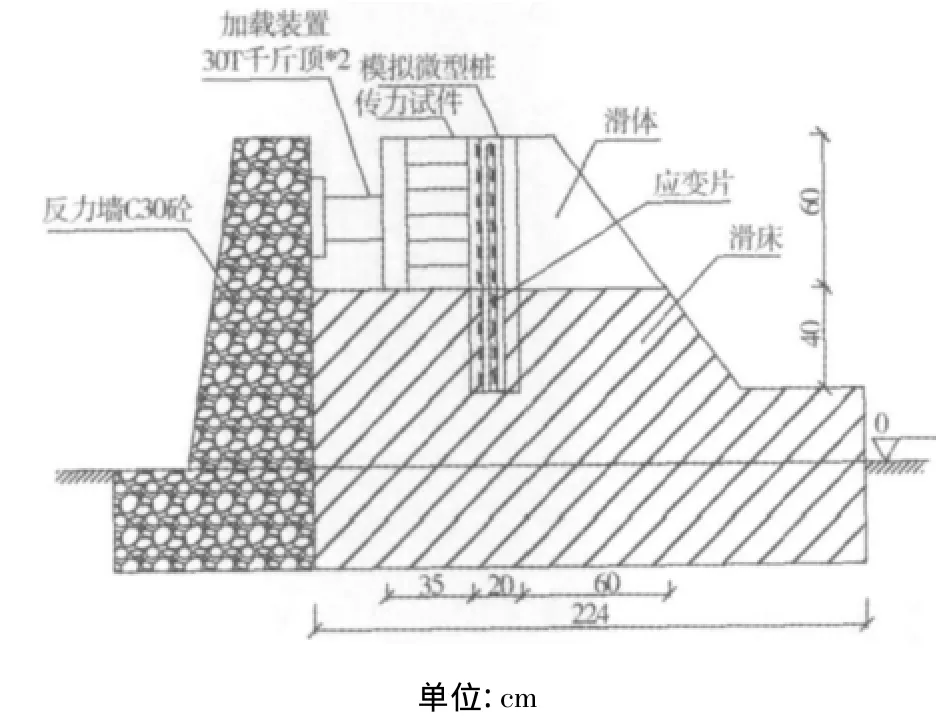
图1 边坡模型图Fig.1 Slope model

图2 试验现场装置图Fig.2 Devices figure of test site

微型桩模型为23.5 mm×30 mm矩形截面的M20砂浆浇筑桩。中心配置直径为6 mm钢筋。2根桩顶部刚性连接形成组合桩，微型桩长1 m，纵向间距60 mm;沿边坡横向布置4排，间距为300 mm。

微型桩嵌固槽中间两组桩为监测桩，沿桩身受拉面每隔10 cm设置应变片，共有监测点40个，采用DH3816数据采集仪采集应变片数据。

1.2 组合桩弯矩分布

根据桩体设置的应变花实测值，得到如图3所示的组合桩在32 kN推力下的桩身弯矩分布图。由图3可知，最大弯矩发生在滑移面附近;前桩弯矩明显小于后桩，前、后桩最大负弯矩之比为0.65左右。

图3 桩身弯矩分布Fig.3 Moment distribution along pile body

2 计算方法

由模型试验结果可以发现，微型抗滑桩组合结构由于桩顶连梁的作用，弯矩在前后桩的分配是不等的，针对该结构特性对前后桩内力分布的影响，暂不考虑桩间土体作用，将模型简化为平面刚架结构，利用位移法讨论结构特性对其影响。位移法是以结构的节点位移(角位移和线位移)作为基本未知量，将杆端力表达成杆端位移的函数，利用位移协调，力的平衡条件建立方程，确定出未知位移，由此，求出整个结构的内力［1］。

2.1 基本假设

计算模型做以下合理简化:

(1)由于微型桩桩间距较小，忽略桩间土提供的抗力，土体提供的抗力集中反映在前桩上。

(2)微型桩只发生顺坡倾向的位移，不发生横向(垂直于滑坡推力方向)位移。

(3)由于横梁的存在，假设2根桩顶的线位移相等。

2.2 计算模型

微型抗滑桩组合结构自由端计算模型如图4，先在原结构的节点C和节点D上装上阻止转动的刚臂约束，而且在节点D上装上1个阻止移动的支杆约束，以此构成位移法的基本结构如图5所示。为了确定出各结点的位移未知量，根据叠加原理，可以把作用于基本结构上的荷载和各结点位移分开计算和叠加。图6表示荷载单独作用下(Z1=Z2=Z3=0)，在各附加约束中产生相应的反力为RIP，R2P和R3P。图7～9所示为单独恢复节点位移时的变形与弯矩，各个附加约束中产生相应的反力rijZj。

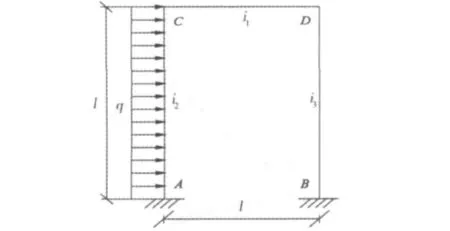
图4 受力模型Fig.4 Mechanical model

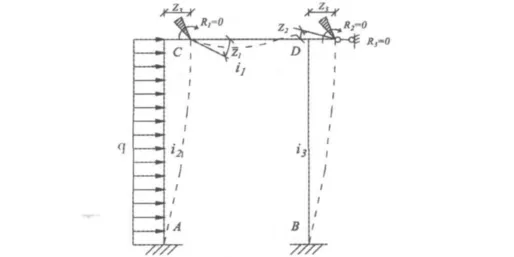
图5 基本结构Fig.5 Basic structure

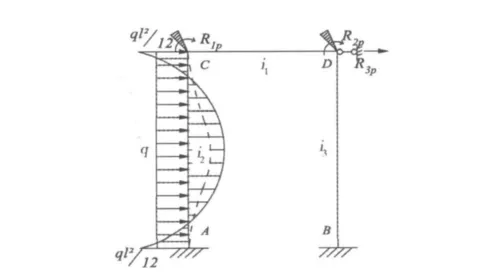
图6 荷载单独作用下弯矩MpFig.6 Moment under load alone

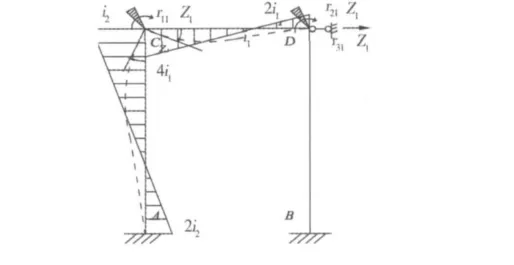
图7 附加约束1产生弯矩M1Fig.7 Moment under constraint M1

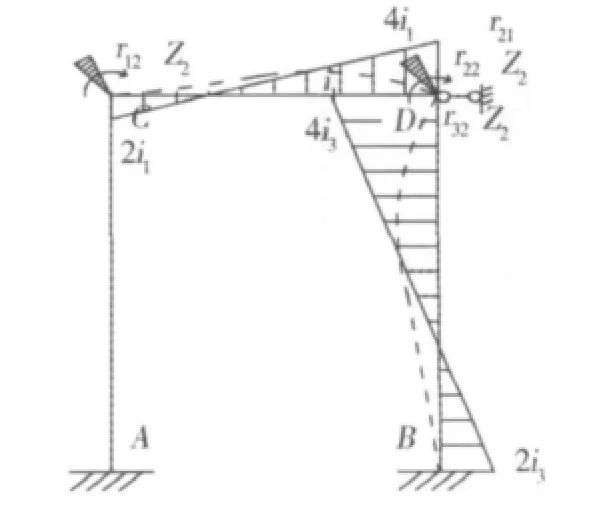
图8 附加约束2产生弯矩M2Fig.8 Moment under constraint M2

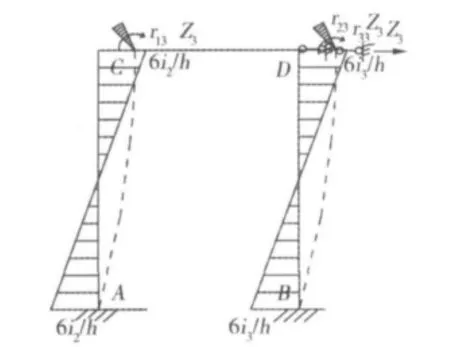
图9 附加约束3产生弯矩M3Fig.9 Moment under constraint M3

将以上变形叠加，由结点C和结点D的力矩平衡和连系梁隔离体剪力平衡得以下方程:

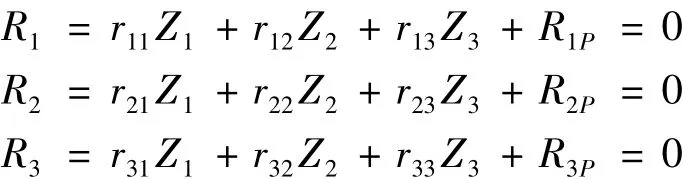
在上述典型方程中，rij表示Zj=1时在各附加约束中产生的反力，由剪应力互等定理，rij=rji，其中RiP表示由于荷载作用在i个约束中产生的反力。

3 算例

本文以2根微型桩体桩顶用连梁连接的微型桩组合结构为例，计算模型简化为受侧向均布荷载的平面刚架。取均布荷载q=20 kN，抗滑桩自由端长6 m，抗弯刚度为EI，连梁长1m，抗弯刚度为EI。根据上述计算模型，得r11=28;r12=r21=12;r22=28;r13=r31=－1;r23=r32=r33=－1;r33=2/3;R1P=60;R2P=0;R3P=－60，带入典型方程求得 Z1=3.57;Z2=13.57;Z3=115.71，根据叠加原理求得微型桩组合结构的弯矩分布如图10所示。

表1 弯矩分布Table 1 Bending moment distribution kN·m

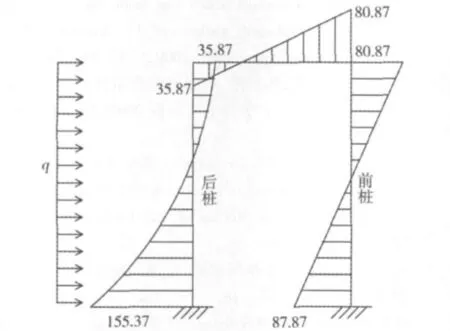
图10 弯矩计算值Fig.10 Slope model

由上述结果看出:由于连梁的作用，后桩弯矩和受力会传递到前桩，前桩桩顶承受负弯矩，桩底承受正弯矩，桩底弯矩略大于桩顶弯矩绝对值。后桩桩顶承受负弯矩，桩底承受正弯矩。计算得到的弯矩分布与模型试验实测弯矩分布较一致，计算得到前后桩最大负弯矩比为0.57，与实测值0.65较接近。

4 组合结构对内力分布影响分析

组合抗滑桩结构对内力的分布影响考虑以下因素:后桩和前桩的抗弯刚度之比λ1=EI前∶EI后，连系梁和桩的线刚度之比 λ2=(EI梁/l)∶(EI桩/h)，荷载 λ3。

4.1 前后桩抗弯刚度之比对弯矩分布的影响

目前设计的微型抗滑桩组合结构大都是前后桩桩径相同，考虑前后桩抗弯刚度不同，将上算例的后桩和前桩的抗弯刚度之比 λ1在0.5，1，2，3，6，9和12工况下弯矩分布如表2所示。

表2 不同λ1下弯矩分布Table 2 Bending moment distribution under differentλ1 kN·m

由以上结果可见:后桩由于直接承受荷载，故最大弯矩值大于前桩，抗弯刚度相同时，后桩最大弯矩接近前桩的2倍。前后桩抗弯刚度相同时，弯矩的分布与抗弯刚度的设置不匹配，造成后桩承受较大弯矩，容易破坏，而前桩没有完全发挥强度，造成浪费。设后桩与前桩弯矩比和抗弯刚度比的比值为匹配系数。提高后桩的抗弯刚度影响弯矩的分布，会改变弯矩的分配，后桩弯矩增大，前桩弯矩减小，匹配系数也随之变化，如图11所示。当后桩与前桩抗弯刚度之比λ1=9时，匹配系数为1，此时，弯矩的分布与抗弯刚度的设置匹配。

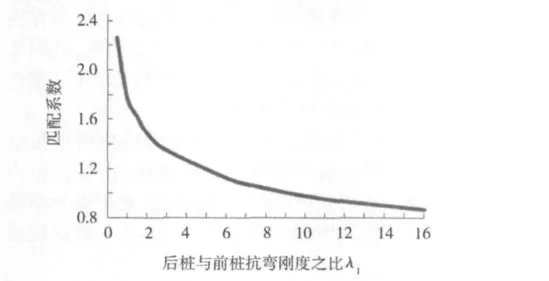
图11 匹配系数随刚度变化图Fig.11 Changes to matching coefficient with stiffness

抗弯刚度主要决定于抗滑桩的桩径，即前桩桩径为0.58倍后桩桩径时，微型桩组合结构最佳。

4.2 连梁和桩的线刚度之比对弯矩分布的影响

连系梁作为前后桩顶的传力结构，其挠度影响到力的传递效果。在上例中，连系梁的线刚度是前后桩线刚度的6倍。不同连系梁和桩的线刚度比作用下，微型桩组合结构弯矩分布如表3所示。

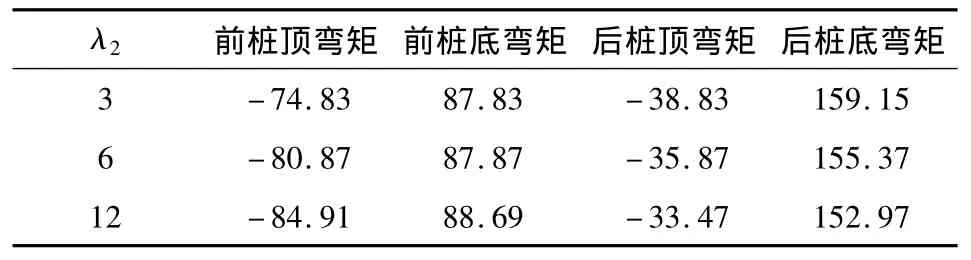
表3 不同λ2下弯矩分布Table 3 Bending moment distribution under differentλ2 kN·m

可见:当连梁的线刚度增大4倍时，前桩桩顶弯矩增大13.7%，后桩最大弯矩减少3.9%，将弯矩更好的分配给前桩，更好地发挥前桩作用。增大连梁的线刚度有2条途径，一是减小两桩的间距，二是增大连梁抗弯刚度。前者受到成孔技术的限制，由于连梁很短，后者对成本增加不大，一般采用后者方法。

4.3 荷载对弯矩分布的影响

不同荷载下弯矩分布如表4所示。从表4可见:弯矩随着荷载的变化几乎同倍变化，荷载变化对前后桩弯矩的分配几乎没有影响。

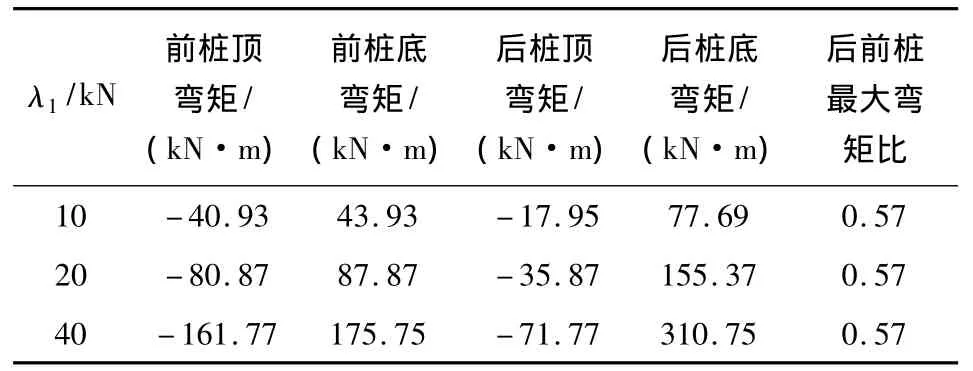
表4 不同荷载下弯矩分布Table 4 Bending moment distribution under different loads

5 结论

(1)由于连梁的存在，前后桩的内力分布存在协调性，后桩产生内力同时会分配给前桩，共同受力，等刚度前后桩弯矩，前、桩弯矩明显小于后桩弯矩，前、后桩弯矩比为0.65左右。

(2)改变前后桩刚度能更好地适应微型抗滑桩组合结构前后桩的弯矩分布规律，前桩桩径为0.58倍后桩桩径时，组合结构最优，处于安全储备考虑，建议工程中前桩桩径取0.6～0.8倍后桩桩径。

(3)组合结构弯矩分配与荷载及前后桩身的抗弯刚度配置有密切关系;连系梁线刚度对前后桩的弯矩的分配有一定影响。

［1］Donald A，Bruce A F，Juran D I.A primer on micropiles［J］.Civil Engineering，1995(12):51－54.

［2］黄伟钦.微型桩在边坡支护中的综合应用［J］.岩石力学与工程学报，2001，20(增1):1218－1220.HUANG Wei-qin.Combined application of micro－piles in slope reinforcement［J］.Chinese Journal of Rock Mechanics and Engineering，2001，20(Suppl.1):1218 －1220.

［3］郭建光，陈 伟，陈晓斌.不同荷载方向下土压力对桩土摩阻力的影响［J］.铁道科学与工程学报，2009，6(6):39－43.GUO Jian-guang，CHEN Wei，CHEN Xiao-bin.Soil pressure explain for load direction eff ects on pile’s friction bearing properties［J］.Journal of Railway Science and Engineering，2009，6(6):39 －43.

［4］丁光文，王 新.微型桩复合结构在滑坡整治中的应用［J］.岩土工程技术，2004，18(1):47 －50.DING Guang-wen，WANG Xin.Application of micropile combination structure in reinforcing landslide［J］.Geotechnical Engineering Technology，2004，18(1):47 －50.

［5］江晓峰.深基坑微型钢管桩与喷锚网联合支护技术应用研究［J］.铁道科学与工程学报，2009，6(3):70－74.JIANG Xiao-feng.Application and research of deep foundation’s united support which was made up of micro －steel pipe pile and spray anchor net［J］.Journal of Railway Science and Engineering，2009，6(3):70 －74.

［6］周德培，王焕龙，孙宏伟.微型桩组合抗滑结构及其设计理论［J］.岩石力学与工程学报2009，28(7):1353－1362.ZHOU De-pei.WANG Huan-long，SUN Hong-wei.Micro－ pile composite structure and its design theory［J］.Chinese Journal of Rock Mechanics and Engineering，2009，28(7):1353－1362.

［7］史佩栋，何开胜.小桩的起源、应用与发展［J］.岩土工程界，2005，8(9):15 －18.SHI Pei-dong，HE Kai-sheng.Origin，application，and development of small diameter piles(IV)［J］.Geotechnical Engineering World，2005，8(9):15 －18.

［8］冯 君，周德培，江 南，等.微型桩体系加固顺层岩质边坡的内力计算模式［J］.岩石力学与工程学报，2006，25(2):284－288.FENG Jun，ZHOU De-pei，JIANG Nan，et al.A model for calculation of internal force of micropile system to reinforce bedding rock slope［J］.Chinese Journal of Rock Mechanics and Engineering，2006，25(2):284 －288.

［9］吴文平，周德培，王唤龙.微型桩结构加固边坡的模型试验与计算探讨［J］.路基工程，2009(3):139－140.WU Wen-ping.ZHOU De-pei，WANG Huan-long.Model test and calculation discussion on side slope strengthened with micro－ pile structure［J］.Subgrade Engineering，2009(3):139－140.

［10］Thompson M J，White D J.Design of slope reinforcement with small－ diameter piles［C］//Geotechnical Special Publication.Reston.USA:American Society of Civil Engineers，1998:67 －73.

［11］龙驭球，包世华.结构力学［M］.北京:高等教育出版社，2000.LONG Yu-qiu，BAO Shi-hua.Structure mechanics［M］.Beijing:Higher Education Press，2000.