Fuzzy聚类分析法在楼盘分类中的应用

王一然，杨柱元，雷靖，2

(1.云南民族大学数学与计算机科学学院，云南昆明650500; 2.云南省软件工程重点实验室，云南昆明650091)

Fuzzy聚类分析法在楼盘分类中的应用

王一然1，杨柱元1，雷靖1，2

(1.云南民族大学数学与计算机科学学院，云南昆明650500; 2.云南省软件工程重点实验室，云南昆明650091)

基于传统的Fuzzy等价关系聚类法，由Fuzzy相似矩阵构建Fuzzy等价矩阵，对传递闭包采用Warshall算法求解，并选择不同置信水平下的分类，利用偏差度得到最优聚类.结合北京市朝阳区近3个月新开楼盘的数据，选择可靠性指标，在最佳置信水平的基础上对其进行最优聚类，实验结果与事实吻合.

Fuzzy等价矩阵;Warshall算法;最佳置信水平;最优聚类

随着数据挖掘技术的发展，聚类分析作为数据分析与可视化的有效工具，广泛地用于数据分析［1］、模式识别［2］和图像处理［3］等方面.聚类分析的基本思想是用相似程度来衡量事物之间的亲疏程度，并以此来实现分类.传统的聚类分析属于硬划分，即把数据集中的每一个数据都精确地划分到某个类中.然而现实事物的数据在属性方面存在模糊性，不存在非此即彼的性质，所以用模糊理论来进行聚类分析更加符合客观实际.正因为聚类分析应用广泛，各种聚类方法也层出不穷，如基于模糊图论的最大树法［4］，由Dunn定义并由Bezdek推广的模糊C－均值聚类算法FCM［5］等，各种方法均有利弊，如FCM算法的缺陷是会陷入局部最优值和初始值敏感的问题.

本文首先对聚类对象进行量纲处理，利用Warshall算法改进传统的平方法求得传递闭包，由Fuzzy相似矩阵得到Fuzzy等价矩阵，选择不同的置信水平下的不同分类，再利用偏差度求得最佳置信水平，并结合有关楼盘数据得到最优聚类，以便客户根据不同需求进行选择.

1 Fuzzy聚类的基本原理

聚类分析的基本原理是用相似度来衡量事物之间的亲疏远近关系，并以此来实现分类.Fuzzy聚类分析的实质则是根据研究对象本身的属性决定的，是基于Fuzzy等价关系进行的分类.

1.1 明确聚类对象

1.2 原数据规格化

由于m个特征标准的量纲级不一定相同，所以在确定相似程度之前先要对数据进行规格化处理，以消除特征指标的量纲差别所带来的影响.数据规格化［6］的方法有很多，如均值规格化、中心规格化等等.在此选取极差规格化方法，则

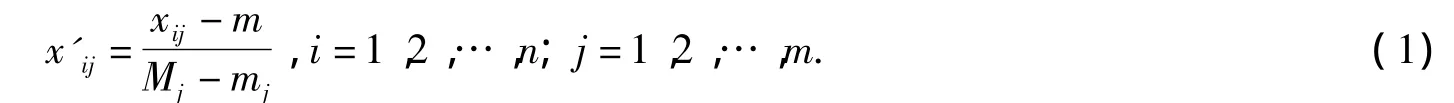
其中

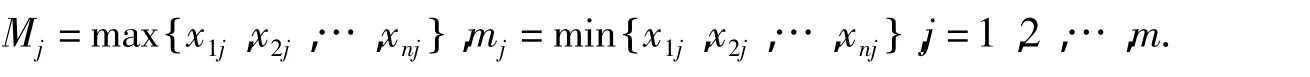
1.3 建立Fuzzy相似矩阵

将数据规格化后，为构造Fuzzy关系矩阵，即为相似关系矩阵［7］，就要用数rij∈［0，1］来刻画对象xi和xj之间的相似程度，即各个被分类对象之间的距离.建立相似矩阵的方法也有很多，例如数量级法、余弦幅度法、最大最小法等等，这里选用绝对值减数法［8］，令

其中c＞0为常数，可以根据实际情况选定，使得rij∈［0，1］.如果rij中出现负值，可以采用下面方法将全体rij进行重新调整.

1.4 改造Fuzzy相似关系矩阵为Fuzzy等价关系矩阵

由于相似关系矩阵一般只满足自反性和对称性，不具备传递性，所以需要将Fuzzy相似关系矩阵改造为Fuzzy等价关系矩阵［6］，一般构造等价关系的方法是用传递闭包法将R改造成为()t R，而此时()t R具备了传递性.而求传递闭包［9］的一般方法是平方法，即为R→R2→R4→…→R2P=()t R，直到某一步RP=R2p时停止计算，求得的RP即为Fuzzy等价关系矩阵.由于此种方法的计算量大、耗时长，所以在此我们将具有计算量小、较为简单等特点的Warshall算法［8］由有限论域的二元关系推广运用到模糊关系上来进行传递闭包的计算.

设有限论域X={x1，x2，…，xi}，R为X上的模糊关系，MR为相应的模糊关系矩阵，通过递归的方法构造n+1个矩阵W0，W1，W2，…，Wn;W0为R的模糊关系矩阵MR，即为模糊关系R的传递闭包的相应矩阵t( MR).计算步骤如下:

1)令W0=WR;

2)假设Ws－1已经求出，则，其中∨、∧分别表示取大、取小值;

3)重复2)的过程，直到求出Wt;

4)根据Wt写出模糊关系R的传递闭包t( R)，算法结束.可以运用Matlab对Warshall算法进行编程计算.

1.5 Fuzzy聚类

Fuzzy聚类的方法有很多，例如编网聚类法、最大树法、Fuzzy C－均值和K－均值聚类算法等等.本文选取的是基于Fuzzy等价关系的Warshall传递闭包方法来进行聚类.上述运用Warshall算法得到传递闭包t( R)后，对Fuzzy等价关系t( R)进行聚类处理，给定不同的置信水平λ，求矩阵t( Rλ)，其中t( Rλ)中的元素属于{0，1}，即得到不同的置信水平下的分类.当λ=0时，被分类对象并为一类，随着λ的不断增大，当λ=1时，又由粗到细，每个对象自成一类，得到动态聚类谱系图.但当λ=0，1时这2种分类本身没有意义.

1.6 最佳置信水平的选择

由于最后得到的是动态聚类，本身分为多少类无从知晓，所以就要选择最佳置信水平［10］λ所代表的分类为最佳分类，在此用偏差度来刻画最佳分类.

定义2设R=(rij)n×n为Fuzzy相似矩阵，Cλ为t( R)λ的λ水平的一个等价类，则称

为Rλ的λ偏差;而称

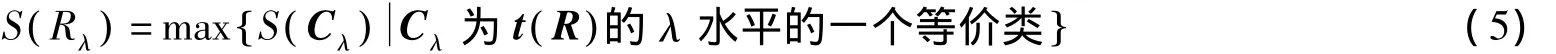
为R=(rij)n×n的λ偏差度.

定义3当选定λ1和λ2，且满足0＜λ1＜λ2＜1，对每一个λ∈[λ1，λ2]，则

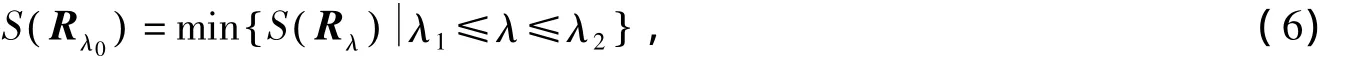
称S( Rλ0)为置信约束[λ1，λ2]之下的最优聚类［10］.

2 模糊聚类在楼盘分类中的应用

选取北京市朝阳区2011年6—9月新开的13个楼盘进行聚类分析，并在借鉴专家经验的基础上选取了6个指标(环境、均价、户型、交通、配套、物业)作为衡量标准.如表1所示.

2.1 数据处理

将表1的数据根据式(1)对数据进行标准化处理，得到矩阵X13×6，根据式(2)得到相似关系矩阵R13×13.

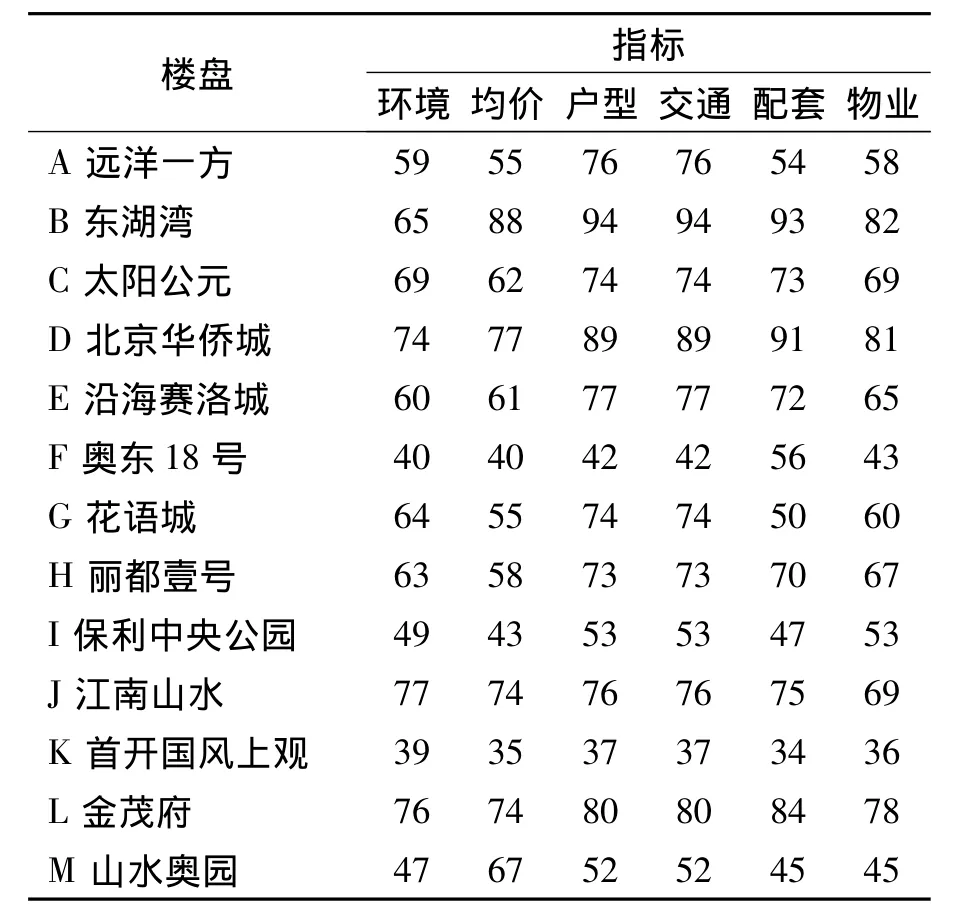
表1 2011年7—9月北京市朝阳区新开盘普通住宅得分(100)

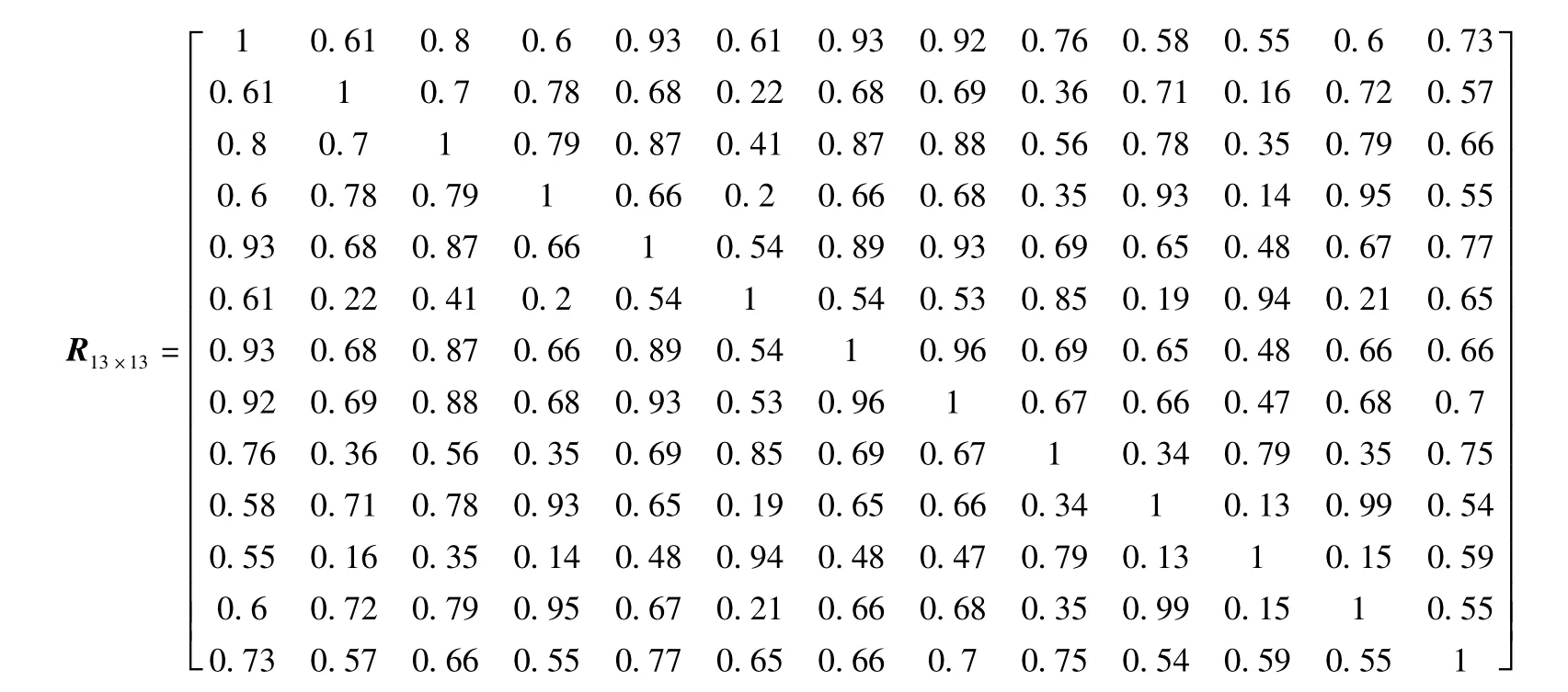
根据Warshall算法得到传递闭包()t R=W6，即为Fuzzy等价矩阵.再根据不同的置信水平λ得到不同的t( Rλ).以λ∈[0.54，0.61)为例，得到t( Rλ).

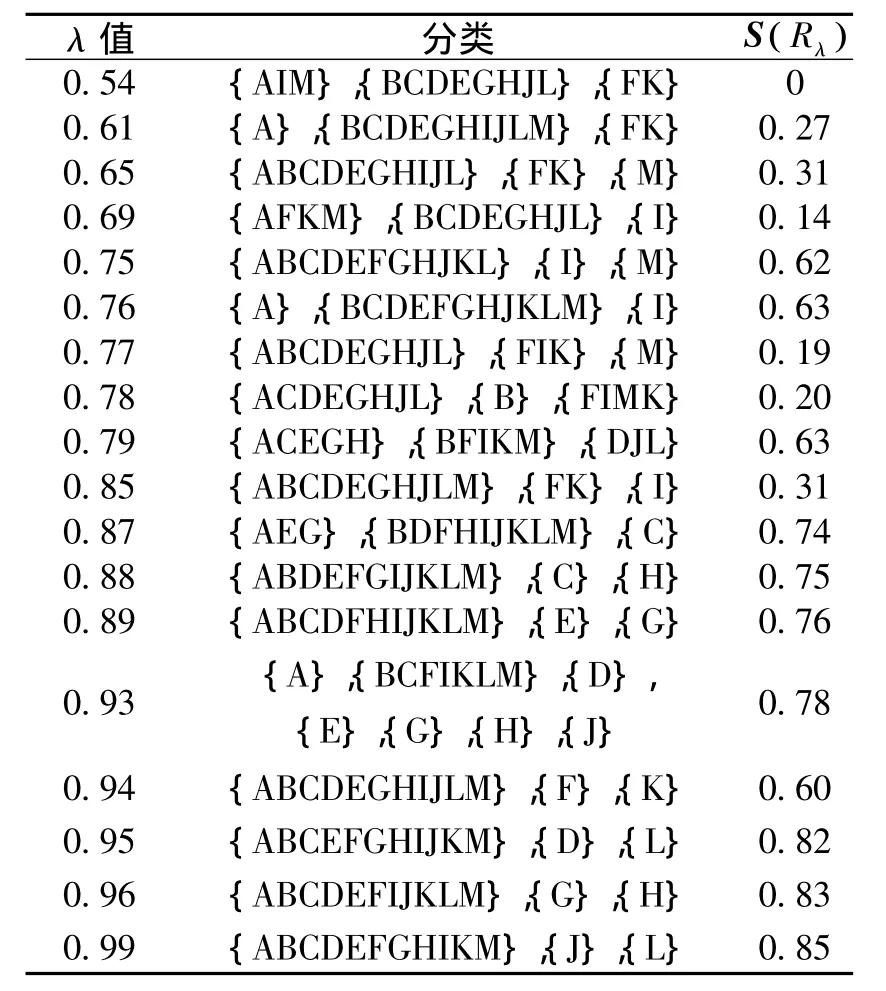
表2 λ值对应的分类及偏差度

由此我们可以得到一个分类，即X分为3类:{AIM}，{BCDEGHJL}，{FK}.并以此类推不同的λ值对应着不同的分类.又因为得到是一个动态聚类图，所以要选出最佳置信水平，从而得到最佳分类.根据式(4)、(5)得到偏差S( Cλ)和偏差度S( Rλ)，见表2.

再根据式(6)得到min{ S( Rλ)}=0，即当λ=0.54时的聚类为最优聚类.

2.2 数据分析

通过分析，将楼盘分为3类.{AIM}的共同点是交通便利，户型设计合理，但是配套设施不健全;{BCDEGHJL}的共同点是房价相对较高;{FK}的共同点是户型偏大.因此通过模糊聚类分析，不同的客户可以根据不同的需求选取适合的楼盘.

3 结论

通过Fuzzy聚类分析对房地产中普通住宅楼盘进行了分类，一方面方便了不同客户根据各人需求选择适合的住宅，另一方面也便于开发商根据不同群体设计和规划不同的楼盘.不过影响决策房地产市场的因素还有很多，比如国家政策影响、当地的经济消费情况等等，所以要对房地产市场进行分类总结还需要全方位地考虑一些潜在的因素.

Fuzzy聚类分析法与软计算方法有着紧密的联系，它是一个不断发展的分析方法，例如将神经网络、灰度聚类、遗传算法［11］等与Fuzzy聚类结合起来的综合研究，所以Fuzzy聚类的研究仍有很广阔的前景.

［1］聂承启，聂伟强，彭云.数据挖掘中的模糊聚类分析［J］.计算机工程与应用，2003，39(33):184－186.

［2］眭志方，张冰，朱志宇.模糊聚类和模式识别在目标识别中的应用［J］.电光与控制，2007，14(4):35－38.

［3］娄银霞，程铭，全惠云.基于FCM和遗传算法的图像模糊聚类分析［J］.计算机工程与应用，2010，46(35):173－176.

［4］陈东升，李科学，赵丽宾.Fuzzy图最大树聚类方法及其应用［J］.运筹与管理，2007，16(3):69－73.

［5］刘坤朋，罗可.改进的模糊C均值聚类算法［J］.计算机工程与应用，2009，45(21):97－98.

［6］胡宝清.模糊理论基础［M］.武汉:武汉大学出版社，2010:192.

［7］郭建华，邓丽娟.基于模糊聚类分析的房地产投资决策评价［J］.商场现代化，2009(20):57－58.

［8］张弢，纪德云.模糊聚类分析法［J］.沈阳大学学报，2000，12(2):73－79.

［9］何小亚，刘杰.求模糊关系传递闭包的一种算法［J］.模糊系统与数学，2006，20(3):83－85.

［10］王秋萍，张道宏.从Warshall算法到求模糊矩阵传递闭包的一个简捷算法［J］.西安理工大学学报，2006，22(3):274－277.

［11］宫尚宝，郭玉翠.基于遗传算法的模糊聚类分析［J］.模糊系统与数学，2010，24(6):123－128.

(责任编辑万志琼)

Application of Fuzzy Cluster Analysis to the Classification of Real Estate

WANG Yi-ran1，YANG Zhu-yuan1，LEI Jing1，2
(1.School of Mathematics and Computer Science，Yunnan University of Nationalities，Kunming 650500，China; 2.Key Laboratory in Software Engineering of Yunnan Province，Kunming 650091，China)

Based on the traditional clustering method for fuzzy equivalence relation，the fuzzy equivalence matrix is structured by the fuzzy similarity matrix，and it solves the transitive closure with Warshall algorithm.Through the classification at different credit levels，the paper gets the best clustering through the degree of deviation and reliability indexes based on the real estate data of the past three months in Chaoyang District of Beijing.The best clustering based on the final optimum credit level proves to be in line with the actual situation.

fuzzy equivalence matrix;Warshall algorithm;optimum credit level;best clustering

O 29

A

1672－8513(2012)04－0266－04

10.3969/j.issn.1672－8513.2012.04.009

2011－10－12.

国家自然科学基金(11061039);云南省自然科学基金(2011FZ169);云南民族大学人才引进基金(2011SE15).

王一然(1987－)，女，硕士研究生.主要研究方向:模糊数据统计.

杨柱元(1964－)，男，博士，教授，硕士生导师.主要研究方向:函数逼近论.