基于摄动理论的压电阻抗损伤识别分析

徐庆军, 郭智刚, 张 峰

(1. 山东高速建设集团有限公司, 济南 250061; 2. 同济大学 土木工程防灾国家重点实验室 上海 200092; 3. 山东大学 桥梁工程研究所, 济南 250061)

基于摄动理论的压电阻抗损伤识别分析

徐庆军1, 郭智刚2, 张 峰3

(1. 山东高速建设集团有限公司, 济南 250061; 2. 同济大学 土木工程防灾国家重点实验室 上海 200092; 3. 山东大学 桥梁工程研究所, 济南 250061)

结合摄动理论和压电阻抗技术监测结构的损伤的发生和定位. 本文利用一阶摄动方法获得了受损简支梁的特征值和模态振型的解析表达式. 通过受损梁的模态振型得到了受损梁的阻抗, 结合PZT与结构的压电耦合电导纳公式得到受损梁的电导纳信号, 采用CC损伤指标评定结构的损伤程度. 以一个受损简支梁为数值算例, 计算了不同损伤条件下其电导纳信号和损伤指标的变化. 当结构损伤位置同PZT之间的距离相同情况下, PZT的CC指标随损伤程度增加有减小的趋势;结构损伤程度相同的情况下, 各损伤工况下的RMSD指标随损伤位置与PZT之间的距离的增加有减小的趋势.

PZT传感器; 压电阻抗法; 摄动理论; 损伤识别; 简支梁

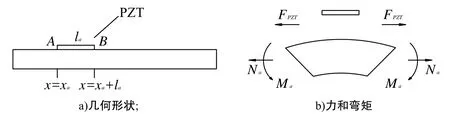
图1 PZT-本体结构相互作用的一维模型

PZT通常用高强度导电胶直接粘贴在本体结构的表面, 粘贴后的PZT在交变电压作用下被看成一个薄片, 仅能产生纵向膨胀和收缩. 其压电方程可表示为:

由式(1)和(2)得到PZT与结构耦合作用下的电导纳公式[14]:

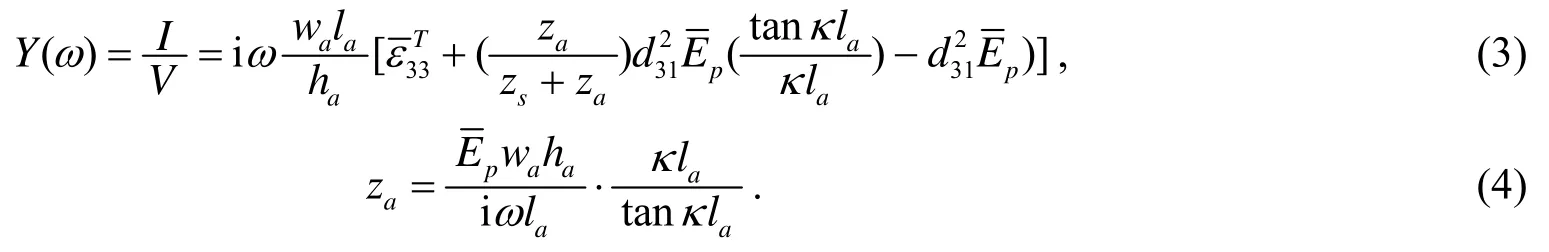
由式(3)中可以看出, 对图2所示的模型,PZT耦合电导纳不仅与PZT的几何尺寸、介电常数、压电常数、杨氏模量、机械阻抗有关, 与所加激励的角频率有关, 还与结构的机械阻抗有关. 对于已经确定的压电系统来说, PZT自身的机械阻抗又是常数, 外部结构的机械阻抗值则是唯一影响第二项的参数, 从而控制压电系统全部导纳Y的变化. 因为结构健康状况的破坏造成外部结构机械阻抗的变化, 则可通过压电元件的导纳反映出来, 也就是说如果机械结构因松动或裂纹等损伤而引起其机械阻抗变化, 则PZT沿z方向的耦合电导纳Y也会发生变化.

PZT在电场谐激励作用下对梁产生一对平衡的轴向力和弯矩, 简支梁的结构阻抗为[13]

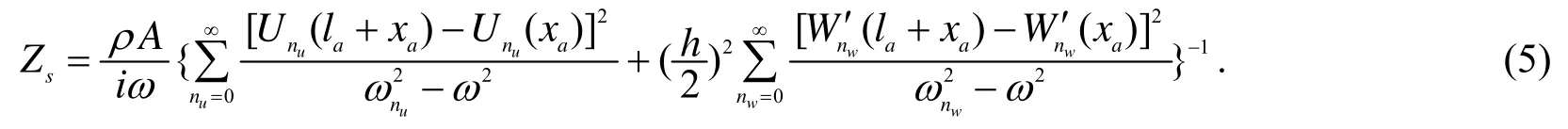
采用一阶摄动理论得到的受损简支梁的轴向自由振动的特征值和模态振型分别为[15]

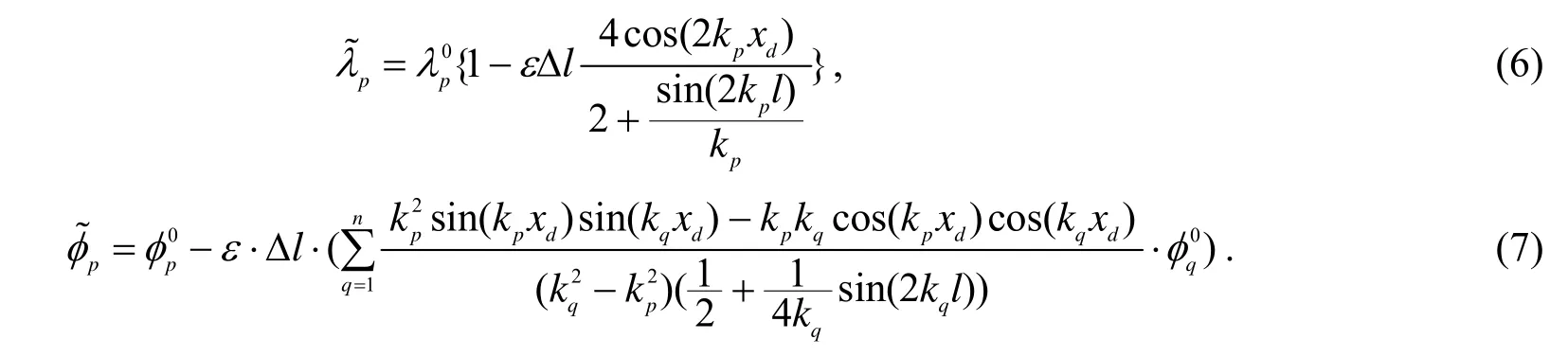
同理, 受损简支梁的弯曲自由振动的特征值和模态振型分别为[15]

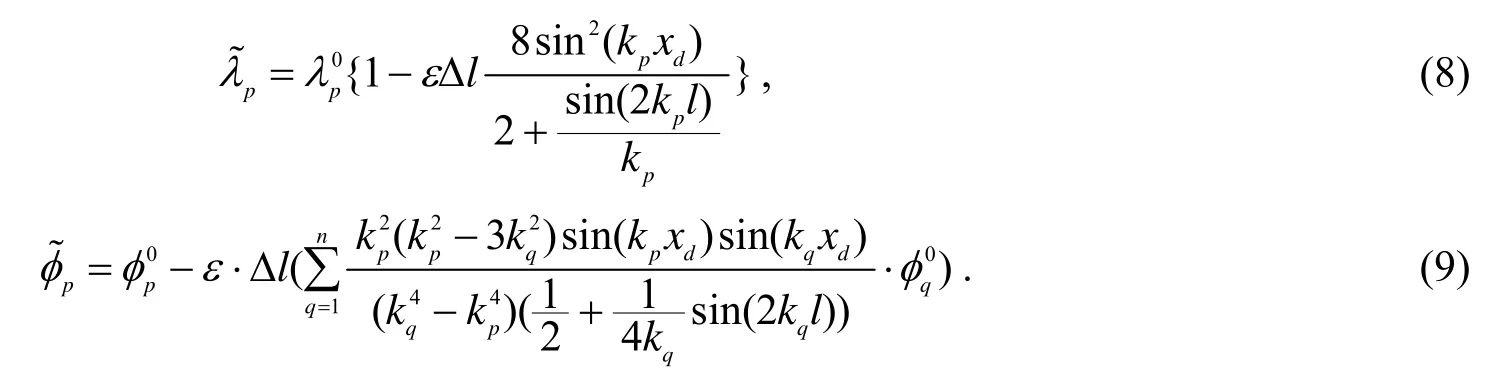
结构出现损伤前后PZT电导纳信号的差异只能定性分析出结构出现损伤, 但不能给出损伤的程度.因此需要定义一个指标, 并用它来衡量结构破坏的程度, 本文引入阻抗协方差(CC)来客观地反应损伤前后阻抗的变化, 即

将式(5)～(8)代入到式(4), 即可得到受损简支梁的结构阻抗, 然后代入式(2)即可求得PZT与简支梁的耦合电导纳信号. 与完整梁的耦合电导纳信号进行比较, 并通过CC损伤指标识别损伤程度和位置.

2 数算值例

现以一个简支梁结构作为数值算例来研究损伤对PZT电导纳信号的影响, 其结构模型如图1所示. PZT和梁的参数见表1和表2, PZT的激励频率为0-3kHz. 图2和图3为PZT位于梁的0.6L处时的损伤深度损伤位置的PZT和梁的耦合电导纳信号的实部和虚部. 从图2和图3可以看出, 梁出现裂纹时, PZT的电导纳信号也随之发生变化.

图4为PZT位于梁的0.6L处时随着损伤深度ε变化而变化的PZT和梁的耦合信号的损伤指标,图5为随着损伤深度ε变化和损伤位置变化而变化的信号的损伤指标. 从图4和图5可以看出,当梁的损伤位置相同时, PZT的CC损伤指标随着损伤程度的增加有减小的趋势. 因此可以根据PZT对梁激励产生电导纳信号获得的损伤指标识别损伤的程度. 图6为PZT分别位于梁的0.2L、0.5L、0.8L处对梁激励产生导纳损伤指标, 损伤深度为损伤位置分别为从图6可以看出随着PZT距离损伤位置的逐步增大, 损伤指标逐步减小. 因此可以采取多个PZT对梁激励产生电导纳信号, 根据损伤指标获得损伤的大致位置.

表1 PZT的机电和几何特性

图2 PZT导纳的实部

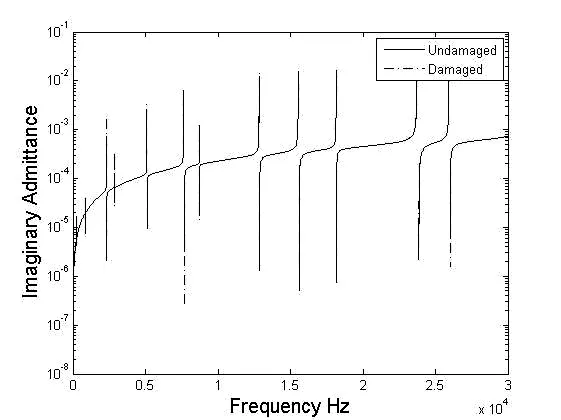
图3 PZT导纳的虚部

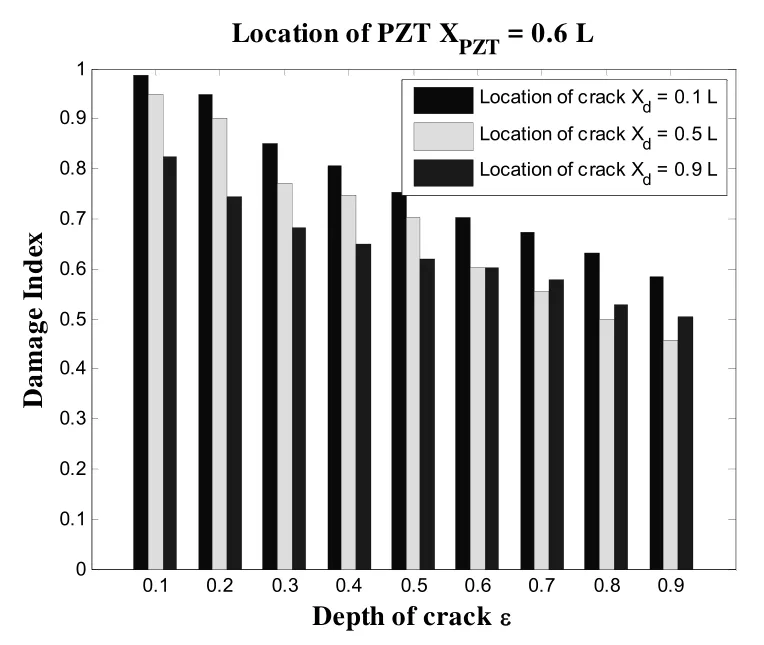
图4 导纳的损伤指标图

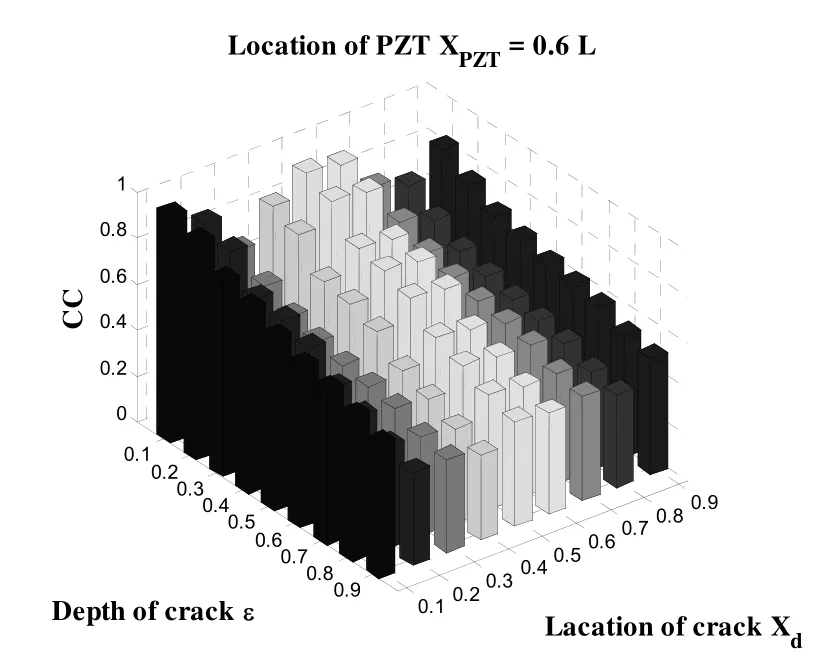
图5 随损伤深度和位置变化的损伤指标

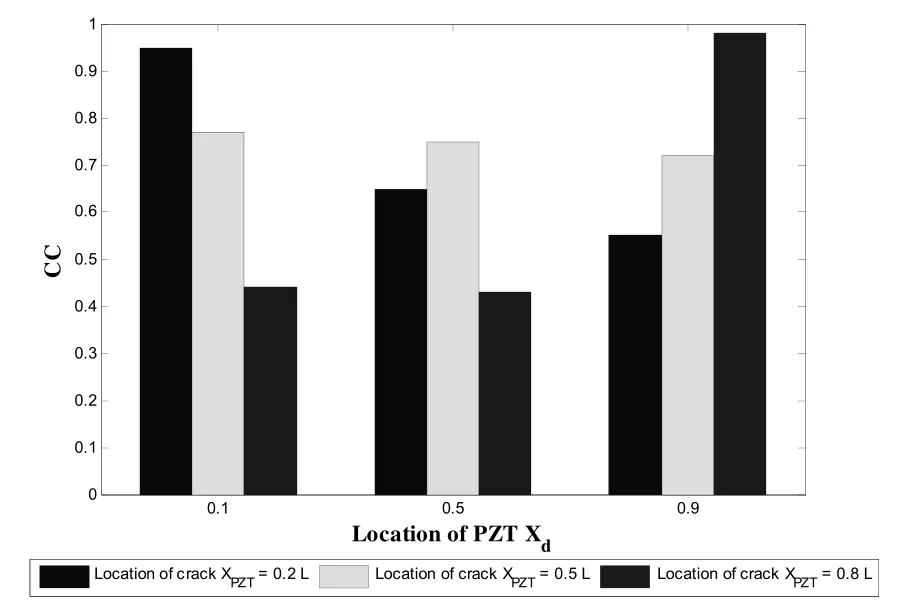
图6 随损伤深度和位置变化的损伤指标

3 结论

本文利用一阶摄动方法得到了受损简支梁的模态振型公式, 并以此得到了受损简支梁的阻抗计算公式, 还利用压电阻抗方法得到了受损简支梁的电导纳信号公式. 从计算公式可知PZT与简支梁耦合作用下的电导纳信号的变化量与损伤尺寸有直接的关系, 从而定性和定量识别结构的损伤程度和位置.

从数值算例得到的结果可以明显地看出, 当梁的损伤位置相同时, PZT的CC损伤指标随着损伤程度的增加有减小的趋势, 因此可以根据PZT对梁激励产生电导纳信号获得的损伤指标识别损伤的程度. 当梁的损伤程度一定时, 随着PZT距离损伤位置的逐步增大, 损伤指标逐步减小, 可以大致识别损伤的位置.

[1] Hera Adriana,Hou Zhikun.Application of wavelet approach for ASCE structural health monitoring benchmark studies[J]. Journal of Engineering Mechanics, 2004, 130(1): 96～104

[2] Park G, Sohn H, Farrar C R, et al.Overview of piezoelectric impedance-based health monitoring and path forward[J]. Shock and Vibration Digest, 2003, 35(6): 451～463.

[3] 焦 莉, 李宏男. PZT的EMI技术在土木工程健康监测中的研究进展[J]. 防灾减灾工程学报, 2006, 26(01): 102～108

[4] 朱宏平, 王丹生, 张俊兵. 基于压电阻抗技术的结构损伤识别基本理论及其应用[J]. 工程力学, 2008(S2).

[5] Giurgiutiu V.,Zagrai A.,Jingjing Bao.Embedded active sensors for in-situ structural health monitoring of thin-wall structures[J]. Transactions of the ASME, Journal of Pressure Vessel Technology. 2002, 124(3): 293～302

[6] Giurgiutiu V, Redmond J M, Roach D P, et al.Active sensors for health monitoring of aging aerospace structures[C]. USA: SPIE-Int. Soc. Opt. Eng, 2000, 3985: 294～305

[7] Lalande F, Rogers C A, Childs B W, et al.High-frequency impedance analysis for NDE of complex precision parts[C]. SPIE, 1996, 2717: 237～243

[8] Chaudhry Z A, Chaudh T J, Sun F P, et al.Local-area health monitoring of aircraft via piezoelectric actuator/sensor patches[C]. SPIE, 1995, 2443: 268～276

[9] Zagrai A. N.,Giurgiutiu V.Electro-mechanical impedance method for crack detection in thin plates[J]. Journal of Intelligent Material Systems and Structures, 2002, 12(10): 709～718

[10] Park Gyuhae,Cudney Harley H.,Inman Daniel J.Impedance-based health monitoring of civil structural components[J]. Journal of Infrastructure Systems, 2000, 6(4): 153～160

[11] Soh C K, Tseng K K, Bhalla S, et al.Performance of smart piezoceramic patches in health monitoring of a RC bridge[J]. Smart Materials and Structures, 2000, 9(4): 533～542

[12] Tseng K K, Wang L.Smart piezoelectric transducers for in situ health monitoring of concrete[J]. Smart Materials and Structures, 2004, 13(5): 1017～1024

[13] Weiping Liu,Giurgiutiu V.Finite element modeling and simulation of piezoelectric wafer active sensors interaction with the host structure for structural health monitoring[C]. USA: SPIE - The International Society for Optical Engineering, 2006, 6174: 61742～1

[14] Liang C.,Sun F. P.,Rogers C. A.Coupled electro-mechanical analysis of adaptive material systems - determination of the actuator power consumption and system energy transfer[J]. Journal of Intelligent Material Systems and Structures, 1994, 5(1): 12～20

[15] Lestari W.Damage of composite structures: Detection technique, dynamic response and residual strength[D]: [Ph.D.Dissertation]. United States --Georgia: Georgia Institute of Technology, 2001

Impedance-Based Method for Nondestructive Damage Identification with Perturbation Theory

XU Qing-jun1, GUO Zhi-gang2, ZHANG Feng3
(1. Shandong Hi-speed Construction Group Co., Ltd, Jinan, 250061; 2.State Key Laboratory for Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China; 3. Bridge Engineer Institute of Shandong University, Jinan 250061, China)

An integrated methodology was presented to detect, locate, and characterize structural damage by combining the impedance-based structural health monitoring technique with a perturbation method. By the virtue of first order perturbation, the eigenvalues and corresponding mode shapes were obtained for the damaged pin-pin beam. Physical changes in the structure cause changes in mechanical impedance which can be achieved by the mode shapes of the damaged beam. The damage index, covariance coefficient (CC), is then proposed for the evaluation of structural damage. A damaged pin-pin beam example has been employed to illustrate the effectiveness of the proposed algorithm numerically, and the change of admittance and CC were calculated under different damaged conditions. The results of numerical simulation studies show that the CC index will decrease with the increase of damage degree if the distance between PZT and damage location is fixed, and the CC index will decrease with the increase of distance between PZT and damage location if the damage degrees are fixed.

PZT transducer; piezoelectric impedance method; perturbation theory; damage identification; pin-pin beam

U448

A

1672-5298(2012)02-0064-04

梁是工程结构中最常使用的一类构件, 在复杂的工作环境下可能会产生裂纹损伤. 但是大量的研究表明[1], 即使结构出现较大损伤, 结构模态参数也可能没有明显变化, 再加上噪声的影响, 现有的许多方法就无法准确识别梁裂缝这样的微损伤. 基于压电陶瓷(piezoelectric ceramic, 简称PZT)电—机阻抗技术(electro-mechanical impedance, 简称EMI)以其对结构初始损伤敏感、对外界环境影响的免疫力强、实用成本低、适宜在线监测的特点得到了越来越多的关注[2～4]. 基于压电阻抗的健康监测技术从提出到现在已经有上十年, 其研究领域主要集中在航空和机械工程[5～9], 近年来在土木工程领域也开展了一定的研究[10～13].本文根据PZT与梁的耦合动态刚度公式得到受损简支梁的阻抗值, 从而得到PZT激励受损简支梁的电导纳信号, 并与完整梁的电导纳信号进行比较, 通过CC损伤指标分析结构损伤对电导纳信号的影响.

1 受损简支梁的阻抗模型

结构的裂纹损伤会引起结构机械阻抗的变化, 但结构的机械阻抗难以通过直接测试得到. 基于阻抗法的结构健康监测技术, 建模时需考虑PZT的动态特征和本体结构的阻抗. 采用一维模型建立PZT与本体结构之间的相互作用(图1).

2012-03-15

徐庆军(1963-), 男, 山东诸城人, 工程硕士, 山东高速建设集团有限公司研究员. 主要研究方向: 道路与桥梁