永磁同步电机速度位置估算法综合分析及验证

祝晓辉， 郭纲， 孙国强， 郭书田

(空军航空大学航空控制工程系，吉林长春 130022)

0 引言

应用非线性状态观测器估计永磁同步电机转子的位置及速度一般建立在转子磁链定向系内，由于其直接针对电机的控制与运行对转角及转速进行估计，因此具有状态估计实时性强、无相位延迟的优点［2－3］。但是，应用文献［1］提出的基于非线性坐标变换后能观测规范形的高增益观测器内核(NTOCF-HGO)实现电机状态的估计存在3个问题:①针对局部及全局观测器，观测器增益的设计与电机实际工作状态的匹配存在一定困难，高增益观测器的特点决定其增益的调节必须兼顾观测器收敛及避免状态反馈造成的高频发散这两方面问题;②文献［1］分析得出永磁同步电机降阶模型方程同时满足局部弱能观及全局能观性，因此观测器的设计及增益的调整一般只针对速度—电流内核，对结合一定位置估算法的两套算法交联收敛机制缺乏必要的证明;③估算法建立在转子磁链定向系内，在电机起动的初始阶段由于转子初始角未知，能否保证稳定起动是无传感器运行亟待解决的关键问题。

本文设计了基于NTOCF-HGO内核的面贴式永磁同步电机速度实时估计的自适应增益调节律，使其满足全局状态估计收敛，且能根据电机实际工作状态用估算得到的交轴电流进行状态估计的稳态及暂态增益调节。将基于直轴电流微分差值修正(RPECM-DDC)的位置角估计算法［4］与本文提出转速估计算法结合起来，位置估计算法运用速度估算法得到的直轴电流微分信息进行偏差修正，证明了两套算法的交联收敛机制。进一步分析得出转速及转角估算法对电枢绕组电阻具有参数变化状态估计鲁棒性，且可应对负载转矩变化对状态估计造成的影响。进行了基于该估算法的永磁同步电机无传感器矢量控制系统级仿真实验，结果表明该算法可以实现一定初始估计误差角的无传感器稳定起动，且具有较好的中低速稳态以及暂态估计性能。

1 速度估计及自适应增益律设计

在无传感器控制策略下，由于转子的真实位置角未知，因此无传感器控制建立在γ-δ估计坐标系上，即与实际转角所在的d-q坐标系相差Δθ=θ－θr角度，如图1所示。

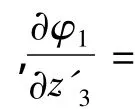
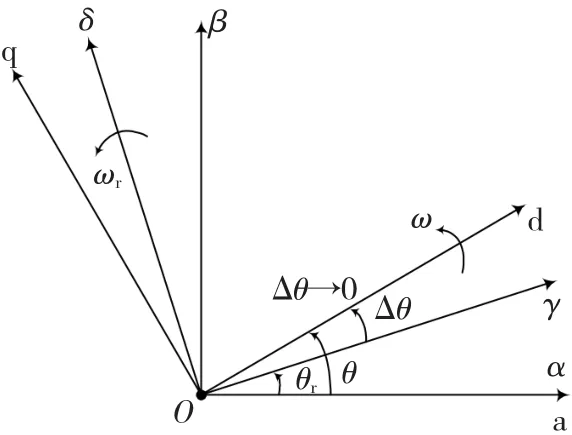
图1 γ-δ及d-q参考坐标系Fig．1 γ-δ and d-q reference frame

对于这种特定结构的基于Σ-I或Σ-II型内核的高增益观测器，观测器的收敛也就是增益的设计由单一常数T(T')决定［5］。T(T')的设计一是要保证具有全局能观性的观测器大范围内状态收敛;二是要根据电机实际工作状态进行幅值调整以满足估计精确度及带宽匹配性要求;其次要控制其幅值使观测器不至因高频成分而产生微分发散。

电机在调速、突加(卸)负载等暂态过程中交轴电流iδ变化比较剧烈，可据此用表征其变化趋势的微分值调节增益使转速估计获得较好内部可控效果。据此设计的自适应增益律为

式中:kq1、kq2为增益电流调节二次项系数;diff(·)表示微分运算符;sat(·)表示饱和运算符;ρ为采样周期内电流^iδ最大允许变化幅度;kω为增益转速调节项常数;kΔi为增益电流调节项上限。

用电流的微分量调节增益常数主要是因为^iδ的变化量真正反映了需要被调节量的动态变化趋势;在允许的电流变化幅度ρ＞0内，增益调节设计成二次型函数可以起到梯度变换效果，有利于增强调整能力;而饱和函数sat(·)的引入则是针对具体系统φ(z，u)的Lipschitz常数限制其增益的上限，避免系统观测出现微分发散。本文在后续仿真实验环节针对实验系统设计包含具体参数的增益调节律。

2 位置估计及交联算法收敛证明

转子位置θr实时估计基本原理为:在γ-δ估计坐标系及转子磁链定向 d-q坐标系内(Δθ=0°，ωr=ω)分别写出电流iγ、iδ及id、iq的状态方程为［4］

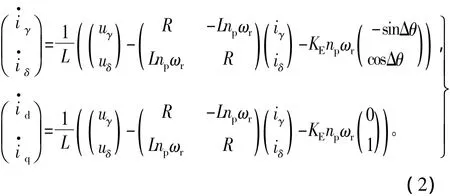
进一步，定义两套坐标系内的电流微分差值为

γ-δ坐标系内电流微分值可以直接经NTOCFHGO观测器输出电流值进行求导求得，而转子磁链定向d-q坐标系内电流微分值则可由式(2)第二式求得。据此，可以得到电流iγ、iδ微分的差值为

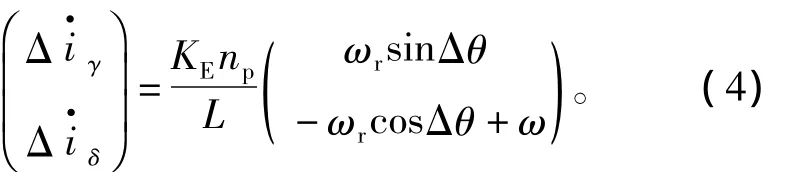
如果Δθ充分小，则有sinΔθ≈Δθ，故由式(4)及Δθ=θ－θr可以得到

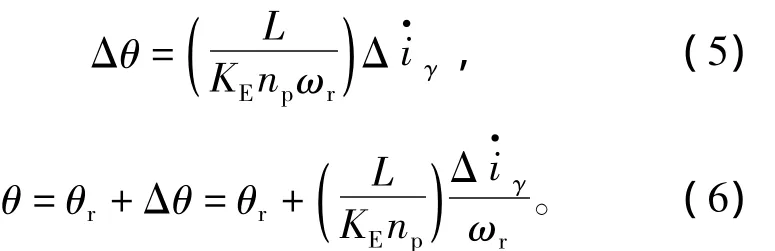
由式(5)可见，转子角估计误差通过直轴电流微分差值Δ及比例系数)得以直观显现，将其作为误差修正量即可得到基于直轴电流微分差值修正(RPECM-DDC)的位置角估计算式(6)。

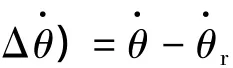
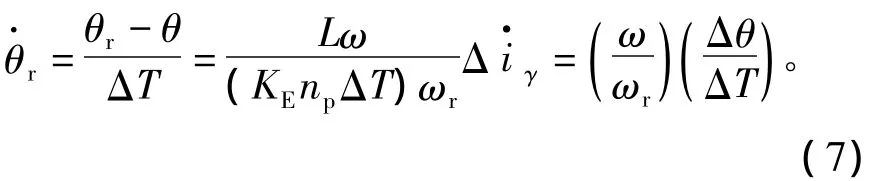
一般情况下，PMSM调速系统电流环采样频率为f=1/ΔT=8 kHz～20 kHz，这使得上述偏差方程具有类似于高增益观测器的快速收敛特性，而电机调速范围一般为0＜ω≤500 rad·s－1，据此可忽略转速项ω对收敛性的影响，最终的偏差方程为

由此可见，转子位置角估计算法具有收敛性。

从算法推导及由式(5)、(6)、(8)可见，位置角θ估算法收敛的一个前提条件是ωr→ω，且其计算过程中需综合利用NTOCF-HGO观测器的全部输出量 ωr以及iγ、;同时，转速估计 NTOCF-HGO 观测器的电压输入uγ(uδ)、电流输入iγ(iδ)及电流反馈)均需经过角θr进行Park旋转变换，转子磁链定向旋转系内NTOCF-HGO观测器法ωr及iγ、iδ估计是否对位置θr估计偏差Δθ具有内在收敛校正机制亦是转角以及转速估计算法可实现性的关键问题，此即为位置速度估计算法交联的收敛性问题。

2.1 观测器内核对输入偏差的有限修正

NTOCF-HGO观测器的输入电压uabc及电流iabc首先经过 Tabc－γδ0变换转换到 γ-δ坐标系，相对于转子磁链定向d-q坐标系变换矩阵Tabc-dq0，其变换后输入量差异矩阵 Δγδ0-dq0(Δθ，θr)如式(10)第一式所示。

所谓NTOCF-HGO观测器内核对输入量偏差的有限修正作用，就是当输入存在这样的旋变误差时，高增益观测器特性使得观测状态追踪真实状态变化趋势且误差幅度控制在允许范围内。这种修正虽然不能完全抵销输入偏差带来的最终的ωr以及^iγ、^iδ估计误差，但对位置交联估计算法收敛的前提条件ωr→ω却是一个内核支撑。

本节继续文献［1］的内核验证流程，在观测器输入端引入经式(10)加权的旋变误差，其中Tγδ0-abc用于将反馈电流iγ、iδ换到静止系后再经Δγδ0-dq0(Δθ，θr)变换引入输入偏移，驱动电压为U=－24.5 V→24.5 V。

图2为基于Σ-II型内核(T'=0.1)的不叠加测量噪声，Δθ=10°以及 Δθ=120°、TL=1.5 N·m 情形下电流及速度估计结果，在小偏差角及大偏差角两种情况下直轴电流iγ估计存在较大的误差，其原因主要是id≈0控制方式使其对误差角比较敏感，交轴电流iδ估计误差相对较小。转速ωr估计在小偏角情况下误差较小，约为1.49%;即使对于Δθ=120°这样的大偏角情形，虽然暂态过程振荡较为激烈且稳态偏差达到－6.27%，但其对式(8)位置角估计的牵引作用足以达到期望的估计效果，可以有效保证算法交联的收敛特性。

研究工作进一步证实:1)如果在暂态过程中调整增益，则可以获得较为平稳的过渡特性，这样就能提高转子位置估计算法的可靠性;2)在叠加不可避免的输出端测量噪声的情况下，电流及转速估计的误差均有所增大。因此，从提高算法交联收敛可靠性的角度来讲，在永磁同步电机实际观测器的设计中增加自适应增益调节律是十分必要的。

图2 Δγδ0-dq0≠0时观测器对状态估计的牵引修正作用Fig．2 Estimation correction of NTOCF-HGO when Δγδ0-dq0≠0

2.2 观测器反馈电流对观测偏差的修正

观测器法对位置θr估计偏差Δθ的收敛校正最终体现在NTOCF-HGO观测器实测电流反馈量id、iq(由ia、ib、ic经 θr旋转变换得到)对观测偏差的修正作用。

与文献［6］状态观测估计偏差校正机制不同，文献［6］设计包含=ωr子系统的全阶模型的局部观测器，其观测偏差校正基本原理是假设电流估计值符合物理系统实际，如果转子位置角θr估计存在误差，则由电机实测电枢绕组ia、ib、ic经θr旋变得到的与观测输出结果相比较产生误差校正信号对观测器系统进行实时修正;本文设计降阶全局能观测子系统NTOCF-HGO观测器，其针对的系统不再是原全阶模型，而是经非线性坐标变换后的中间系统，高增益观测器的特性使速度估算内核对由于转角差引起的输入偏移具有较强牵引修正作用，此时结合外部转角估算法RPECM-DDC可以在相邻几个电流采样周期内迅速达到状态估计收敛，应用收敛的转角θr→θ对电机终端实测电流进行旋变，可进一步提高内核速度及电流的估计精确度，从而保证两套交联算法最终达到稳定收敛。

两套算法相互作用机制可用图3所示信号流程给予说明。

图3 NTOCF-HGO速度估计内核及外部RPECM-DDC转角估计算法收敛机制Fig．3 Inherent convergence mechanism of the two algorithm

3 参数摄动状态估计鲁棒性分析

在旋转坐标系内构造经非线性变换后系统的高增益状态观测器，其状态z=Φ(x)及z'=Φ(x')的估计对参数变化具有内在鲁棒性。考虑到随电机温升而发生变化的定子电阻值可表示为=R+ΔR，将其代入基于Σ-I型内核的NTOCF-HGO转速估计式 ωr==+α1)/，则可以得到

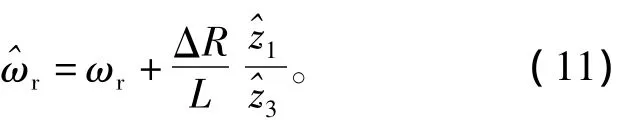
由于电机工作于id≈0状态，此时由高增益观测器的特点可以得到=iγ≈0，因此基于Σ-I型内核转速估计对电阻变化具有较强鲁棒性。同理，考虑到定子电阻温升摄动，并将其代入Σ-II型内核转速估计式ωr=，可以得到

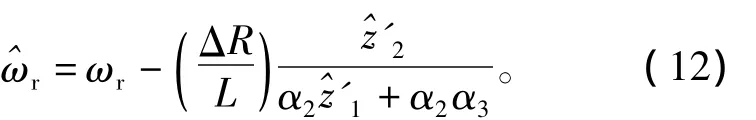
考虑到=iγ≈0，并且将参数 α3=代入式(11)，则可以推导出)，由此可以证明:相对于转速的数量级，基于Σ-II型内核的转速估计同样对电阻变化具有较强鲁棒性。

同理，将=R+ΔR代入式(2)可以得到

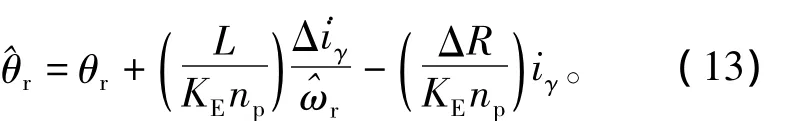
由id≈0控制方式可知，转子位置估计对定子电阻温升摄动亦具有较强鲁棒性。

其次，根据高增益观测器的结构特点，外部转矩作为输入可一并视为φ(z，u)的组成部分，因此该观测器具有较强的抑制转矩扰动的能力。由高增益观测器的特点可取TL－in=(0～100)%TL，为了减小增益的设计与调节负担，一般可设置为TL－in=(60～100)%TL。

4 主要仿真实验结论

根据以上分析，可以得到转子位置及速度估算的最终流程图如图4所示。

图4 转子磁链定向坐标系内位置角及速度估算流程图Fig．4 Estimations diagram for the rotor speed and position

PMSM-SVC系统仿真主要从数值分析角度验证转速及转子角交联估计算法的有效性，为此依据模型简易程度、矢量控制原理及模拟实际系统的近似度将数值仿真分为算法级验证及系统级验证两个层次。

4.1 算法级验证结论

算法级验证主要是在模拟矢量控制基本原理的基础上分析转角及转速估计算法可实现性问题。永磁同步电机矢量控制的本质是建立在转子磁链定向坐标系内的解耦控制，而本文提出的转子状态估计算法也是建立在该旋转系内，因此，对转子磁链定向旋转系内控制量的模拟是仿真算法设计的关键，NTOCF-HGO速度估计以及RPECM-DDC位置估计都依赖于交、直轴控制电压及反馈电流的合理模拟。仿真模型的参数同文献［1］。

电压驱动主要完成PMSM-SVC矢量控制系统d-q系、γ-δ系驱动电压的协同模拟。矢量控制驱动电压顶层设计为考虑功率因数角的交、直轴电压的生成，将此生成电压作用于电机的全阶模型即可得到电压相角，据此通过反Park变换得到静止系驱动电压;设定初始状态角由d-q系统模型可得到自同步驱动电压ud、uq;将此电压经同步角θ反旋到静止系再与转子角估算值θr进行正旋变换就得到速度估计模块及转子角估计模块驱动电压uγ、uδ。这种方法模拟了矢量控制方式下驱动电压设计，且由于其保持了与估算模块的同步性，使得模型响应电流id、iq可以替代iγ、iδ直接用于下级估算法的反馈校正及算法驱动。电流反馈及驱动设计与电压驱动的设计类似，其功能是实现电流变换:idq→iγδ。

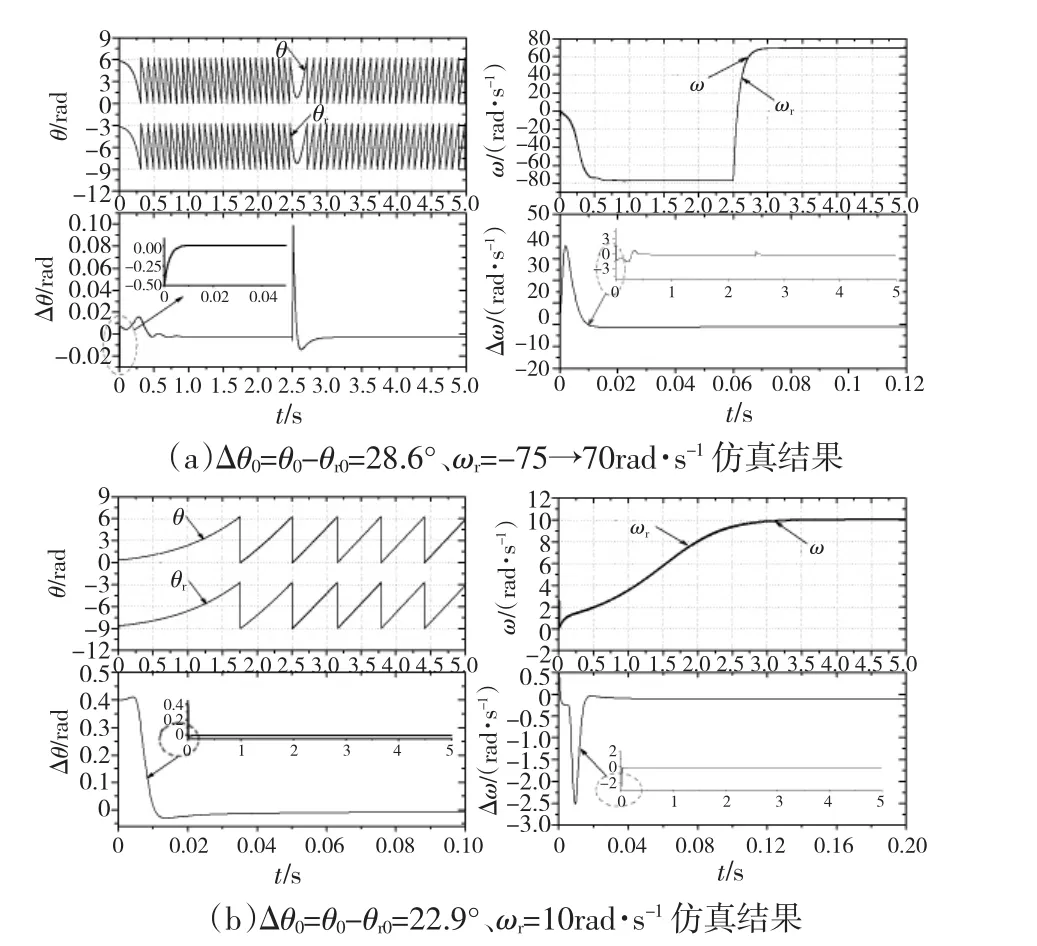
图5 算法级仿真实验结果Fig．5 Simulation results at the algorithmic level

由于算法级仿真不考虑实际物理系统存在的噪声，因此暂不在程序中引入增益自适应律。图5为采用基于Σ-II型内核观测器、转角初始误差Δθ0=θ0－θr0=28.6°的情形下无传感器起动至稳定工作状态的仿真结果，其中在2.5 s处转速发生翻转，用于模拟系统大范围暂态过程情形，负载转矩TL=1.5 N·m。转角估计如图5(a)第1图所示，起动仿真程序后估计转角迅速收敛到真实值，转速发生翻转时经小幅振荡回归真实位置状态;转速估计如图5(a)第2图所示，采用NTOCF-HGO技术可保证转速估计快速精准。低转速情形下的仿真结果如图5(b)所示，本例估算模块反馈及驱动电流由模型实际电流经估计位置变换得到，稳定起动的初始偏差角有所降低，但转速及转角估计效果良好，证明了所提出方案具有较好的低速特性。

4.2 系统级验证结论

算法级验证是在旋转系内通过自主设置外部驱动电压对转子位置及速度估算法进行验证，而系统级仿真进一步通过模拟无传感器控制以及状态估计各环节运行的实际状况对所提方案的可行性进行验证。

图6为基于Σ-II内核的存在一定初始角偏差情况下采用固定增益常数值T″=0.01及负载转矩恒定的估计结果(Δθ0= θ0－ θr0=28.6°)，速度指令经调整确定为图6(b)所示稳定的连续阶跃及反转工作状态，增益固定的情况下，高速及低速工作状态转速与转角估计结果发散的主要原因是NTOCFHGO观测器不能在较大范围内保证Lipschitz常数幅值有界，图中各工作状态急剧变化处估计结果出现较大偏差亦由此产生。

图6 转角及转速实际值、估计值与估计偏差Fig．6 Actual and estimated rotor position and speed

观测结果表现为发散或围绕常值不等幅振荡的另一重要原因是NTOCF-HGO及RPECM-DDC的驱动电流iγ、iδ与电压uγ、uδ受控制器的品质影响较大，且实际系统电流传感部件受检测噪声干扰，使得其有效信息湮没于较宽频带分布范内的噪声信号中，由此使估计算法呈现微分发散的不可逆结果。解决的方案一是通过估计算法内部增益的自主调整达到对状态跟踪效果的控制;其次，也是最根本的解决方案就是改善控制器的品质，使电机终端电流中包含除少量高频扰动量以外的能充分反映系统动、静态驱动信息的低频有效主导成分。

图7为低速无传感器运行带增益自主调整与采用固定增益两种情形下转速的估计结果(转角初始误差设置为零)，增益律各参数设置为:ρ=2、kω=2 000=0.01、kq1=0.02、kq2=0.01。可以看出:在模拟实际控制系统一个采样周期时间段内，与采用固定增益值估计发散的结果相比较，根据交轴观测电流的变化趋势对增益常数进行实时调整，可以有效地改善低速估计效果。

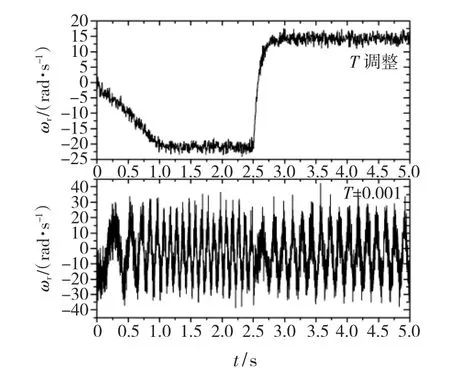
图7 低速情形下应用增益自适应律前后NTOCF-HGO速度估计Fig．7 Estimated rotor speed with and without adaptive gain

图8为参考图6所示工作状态设置基础上，模拟绕组电阻值R由于温升增加10%、25%、50%情形下的转角及转速估计误差。可以看出:动态调整阶段的估计偏差受电阻值变化影响较大，但在保证估计算法收敛的前提下，本文提出的方案对电阻参数摄动具有较强的状态估计鲁棒性。

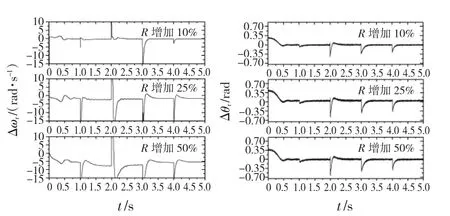
图8 模拟电阻温升10%、25%、50%情形下状态估计偏差Fig．8 Estimated error with rotor resistance increases

其次，由NTOCF-HGO观测器设计特点可知，外部转矩输入驱动项TL可一并归入到非线性项φ(z，u)中，因此参照电阻参数变化状态估计鲁棒性分析方法可对其进行区间化处理，此估计方法符合负载转矩不易辨识的实际系统应用的特点。算法级及系统级综合仿真证明本文提出的转角及转速估计方案的可行性。

5 结论

本文在文献［1］提出的 Σ-I型及 Σ-II型 NTOCF-HGO观测器的基础上，设计了面贴式永磁同步电机速度实时估计的自适应增益调节律，在此基础上，将基于直轴电流微分差值修正的位置估计算法与本文提出转速估计算法结合起来，证明了两套算法的交联收敛机制。算法级及系统级仿真表明，该算法可以实现一定初始估计误差角的无传感器稳定起动，具有较好的中低速稳态以及暂态估计性能。为了提高算法应对高频扰动量的能力，本文后续将研究改善控制器品质，使电机终端电流只包含低频有效成分的问题。

［1］祝晓辉，李颖晖，陈亚滨．基于非线性状态观测器的永磁同步电机无位置传感器矢量控制［J］．电工技术学报，2010，25(1):50－57．ZHU Xiaohui，LI Yinghui，CHEN Yabin．Sensorless vector control for PMSM based on nonlinear state observer［J］．Transactions of China Electrotechnical Society，2010，25(1):50－57．

［2］XU Junfeng，WANG Fengyan，XIE Shaofeng，et al．A new control method for permanent magnet synchronous machines with observer［C］//The 35th Annual IEEE Power Electronics Specialists Conference，June 20 －25，2004，Aachen，Germany．New York:IEEE，2004，1404－1408．

［3］TECK-SENG Low，TONG-HENG Lee，KUAN-TECK Chang．A nonlinear speed observer for permanent-magnet synchronous motors［J］．IEEE Transactions on Industrial Electronics，1993，40(3):307－316．

［4］Ali Khurram．Position and speed sensorless control of Permanent Magnet Synchronous Motors［D］(for the degree of Doctor of Philosophy)．Michigan USA:Michigan State University，2001．

［5］Bonard G，Hammouri H．A high gain observer for a class of uniformly observable systems［C］//IEEE Proceedings of the 30thConference on Decision and Control，December 11－13，1991，Brighton，UK．New York:Institute of Electrical and Electronics Engineers，1991:1494 －1496．

［6］L．JONES，J．LANG．A state observer for the permanent-magnet synchronous motor［J］．IEEE Transactions on Industrial Electronics，1989，36(3):374 －382．