压电陶瓷执行器多模时变滑模逆补偿控制

赖志林， 刘向东， 陈振， 任宪仁

(北京理工大学自动化学院，北京 100081)

0 引言

压电陶瓷执行器具有推力大、响应快、精度高等诸多优点，在半导体制造、生物医学、航天航空等许多尖端科技领域中发挥着越来越重要的作用［1－2］。然而，压电陶瓷的迟滞及蠕变特性，给压电陶瓷的精确控制带来了很大困难。许多学者为此提出了很多迟滞补偿的控制方法。为了减弱迟滞非线性对控制的影响，一般采用迟滞逆模型对压电陶瓷的迟滞进行逆补偿线性化。然后设计控制器对线性化后的压电陶瓷进行控制。Ge和Jouaneh用数值方法实现基于Preisach模型的前馈控制，利用PID控制器进行反馈控制，较好地抑制了迟滞特性对系统的影响，提高了控制精确度［3］。Shen通过改进的PI模型建立迟滞的逆模型，并且设计了带有滑模扰动观测器的滑模变结构控制器串联在迟滞系统之前，其控制效果在实验平台上得到了验证［4］。文献［5］用反馈误差学习方法，快速地在线得到压电陶瓷的逆模型，结合PlD反馈控制，在dSPACE系统平台上实现了压电陶瓷的神经网络自适应逆控制，并且控制效果比PID有明显提高。文献［6］提出了一种基于极坐标的数学建模方法，在该迟滞模型的基础上，引入前馈PID控制方法进行实验，实验结果表明，该方法具有较高的跟踪精确度和较好的线性度。

为了实现压电陶瓷的精确控制，本文采用Preisach模型建立压电陶瓷执行器的迟滞逆模型，并利用逆模型对迟滞进行串联补偿。针对补偿后的线性模型，设计了滑模控制器进行控制。为了减小稳态误差，选取的滑模面中加入了对误差的积分。并且为了实现全局鲁棒性及减弱由于对误差积分带来超调等影响，本文设计了两种不同滑模面的滑模，并且利用多模控制的思想进行控制。另外，本文采用了模糊控制理论对多模控制中的切换时间进行调节，使得两种控制之间平滑地切换。本文设计的时变滑模控制器，在实验平台上得到了验证。

1 压电陶瓷执行器

压电陶瓷叠堆驱动器是由单片的压电陶瓷片并联而成的如图1所示。其内部等效结构如图2所示。压电陶瓷片层间使用银、石墨合金作为内电极，每隔一层的内电极形成玻璃绝缘膜，再装上外电极，形成并联连接。理想情况下，压电陶瓷叠堆驱动器的伸缩量与驱动电压之间是简单的线性比例关系。但实际上，由于压电陶瓷极化机理和机电耦合效应等的影响，压电陶瓷叠堆执行器还存在着迟滞、蠕变等非线性特性［7］。文献［8］把压电陶瓷执行器看成是非线性部分(主要为迟滞非线性Γ(－))和线性部分G串联组成。如果把非线性部分看成是系统的扰动，则压电陶瓷执行器的状态方程可表示为

c =[1 0 ]，u，r，y∈R1。r为压电陶瓷输入，y为压电陶瓷输出，u为迟滞输出，d为系统扰动，n为干扰。写成分量形式的方程为

其中:x1为压电陶瓷执行器输出的位移;x2为速度;T为时间常数;ξ为阻尼比;K为系统增益。

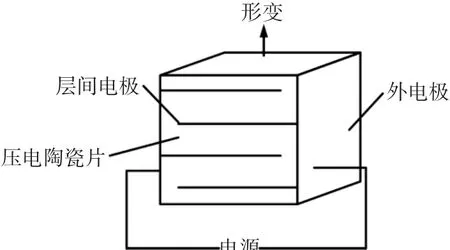
图1 压电陶瓷结构Fig．1 Structure of the PA

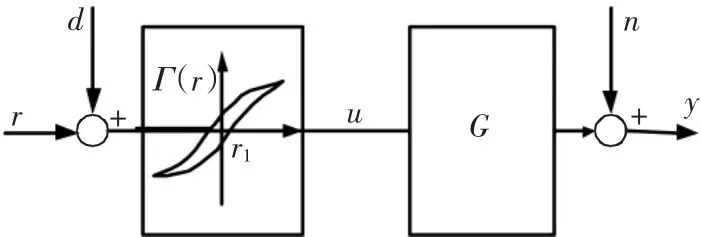
图2 压电陶瓷内部等效结构Fig．2 Equivalent structure

2 基于Preisach逆补偿的多模时变滑模控制律设计

为了降低压电陶瓷执行器迟滞非线性，在控制系统中采用逆迟滞模型对压电陶瓷执行器的迟滞进行补偿。补偿后可以等效地把压电陶瓷执行器看成一个线性对象G。文献［9］中采用Preisach分类排序的方法建立迟滞逆模型，并且针对线性部分设计了时变滑模控制器。这种滑模逆补偿控制策略消除了滑模控制的到达阶段。为了进一步提高滑模控制的精确度，在滑模面上加上了积分项用于消除稳态误差。然而，积分项的加入容易引起超调。为了解决这种滑模控制中存在的问题，设计了基于Preisach逆补偿的多模时变滑模控制律。

如图3所示，如果不考虑干扰及模型不确定性等影响，逆补偿后的系统方程(2)中的输入及扰动:u=uc，d=0，n=0。

图3 压电陶瓷执行器的滑模逆控制Fig．3 SMC of the PA based on the inverse compensation

定义位移误差为

其中:y为系统的输出位移;fr为系统的期望位移输入。

设计具有指数收敛［10］性质的时变滑模面为

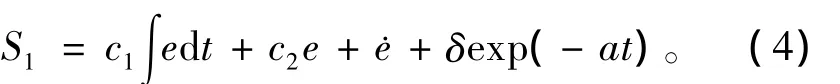
其中:δ，a∈R。c1＞0，c2＞0 是常数。

当t→∞时，滑模面变为

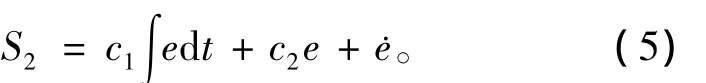
为实现滑模控制的全局鲁棒性，在初始时刻系统相轨迹需处于时变滑模面上，令S1=0，可得

当系统在滑模面上滑动时有

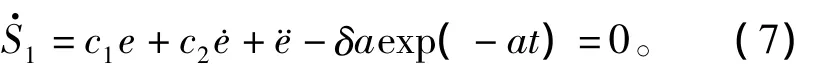
式(1)与式(7)两方程联解得到等效控制量为

则滑模控制器输出控制量为

其中，定义usw=ηsgn(S1)，η＞0为切换控制量增益。

另外，为了消除抖振，设切换控制量usw=ηS1，则滑模控制器的输出量为

定义Lyapunov函数为

对式(11)两边对时间求导可得

在实际中，由于逆模型的不精确性，迟滞非线性不能完全抵消，设没被抵消部分为ΔΓ。另外，考虑干扰及模型不确定性等影响，d≠0、n≠0。所以，控制对象的输入为

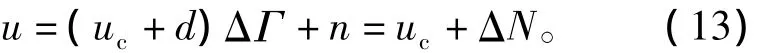
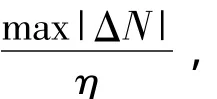
采用式(5)所示的滑模面，因为引入了积分项，有利于消除系统的静态误差，提高系统的跟踪精确度。但是，在系统跟踪初始阶段，由于误差较大，在积分的作用下增大了系统的超调，并且影响了滑模的到达阶段。

为此，设计了两个滑模控制器，采用多模控制的方案。在滑模的初始阶段采用没有积分项的滑模面为

当系统的输出跟踪上输入后，此时误差较小，把积分项加入到滑模面中，如式(5)所示。

当滑模面取为S3时，可以得到控制量输出为

其中，ueq1为等效控制。usw1=η1sgn(S3)，η1＞0 为切换控制量增益。

由以上分析可知，在初始阶段，选用没有积分项的滑模面S3;当跟踪误差较小时，切换到有积分项的滑模面S1上，由此构成一个多模切换系统。传统的切换过程直接采用误差或者时间的阈值，但是这种固定的阈值容易使得切换过程产生一定的波动，不够平滑。为了使得积分项平滑地加入，采用了模糊理论，得到切换的时刻。如图4所示。

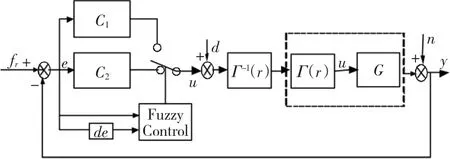
图4 多模控制系统结构Fig．4 Multi-mode control system

模糊控制器中的输入量为误差e和误差导数e，输出为切换的时间t。根据实际试验情况，定义误差e及误差导数e变化范围为模糊论域，即

其模糊集均为{NB，NS，ZE，PS，PB}，表示负大，负小，零，正小，正大。隶属度函数选用常见的等腰三角形。

切换时间t的取值论域为［30n，100n］。这里n为控制周期。同样分为{NB，NS，ZE，PS，PB}。

模糊规则是指如何从控制器输入得到控制器的输出。根据误差及误差变化率的情况确定切换时间，使切换点的误差小，且没有误差增大的趋势。具体规则如表1所示。

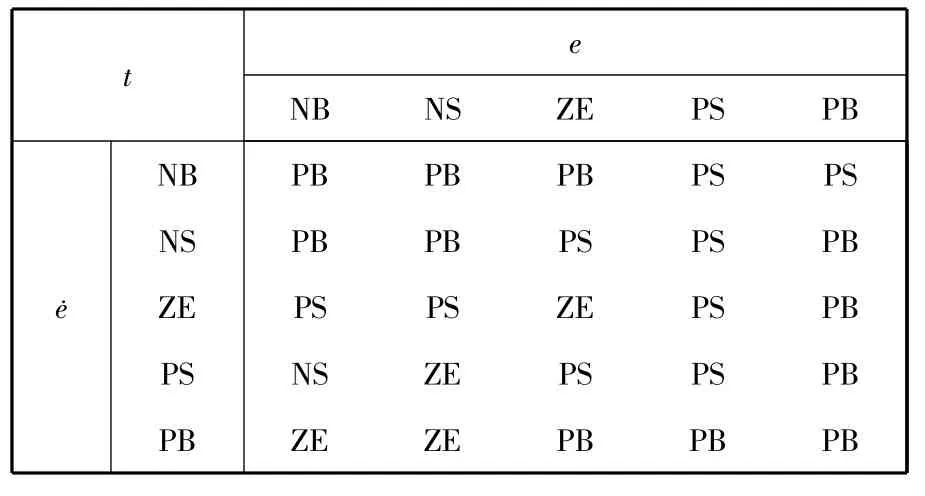
表1 模糊规则表Table 1 Fuzzy rule

最后把由模糊推理得到的模糊量转换成精确的切换时刻值。这里选用重心法得到具体的切换时间。

3 实验研究

为了验证本文方法的有效性，开展了压电陶瓷执行器滑模+逆控制实验研究。在实验中，控制器用TI公司TMS320LF2407做控制器件，数模及模数转换分别是16位的AD669及AD976，控制器通过串口把采集到的数据传给上位机。压电陶瓷执行器平台是MPT－1JRL/I002，此平台内部安装电阻应变片位移传感器。压电陶瓷执行器的耐压范围为－30～150 V，输出位移范围为0～15.02 μm。驱动电源为HPV系列压电陶瓷驱动电源。

根据Preisach逆模型分类排序数学实现公式可知，可以通过插值的方法实现迟滞逆模型。具体步骤在文献［6］中已经给出。

压电陶瓷执行器的线性部分模型参数可以通过线性辨识方法得到。压电陶瓷执行器的状态方程参数如下:K=1，T=2.329 ×10－4，ξ=0.681 3。

在实验过程中，给压电陶瓷执行器输入1Hz正弦曲线u(i)=5－3×sin(π/2－π×i/200)，其中i为采用点数。

为了说明压电陶瓷执行器迟滞非线性的对控制精确度的影响，首先给出开环控制时的跟踪情况及实际位移和期望位移之间的拟合图，如图5及图6所示。

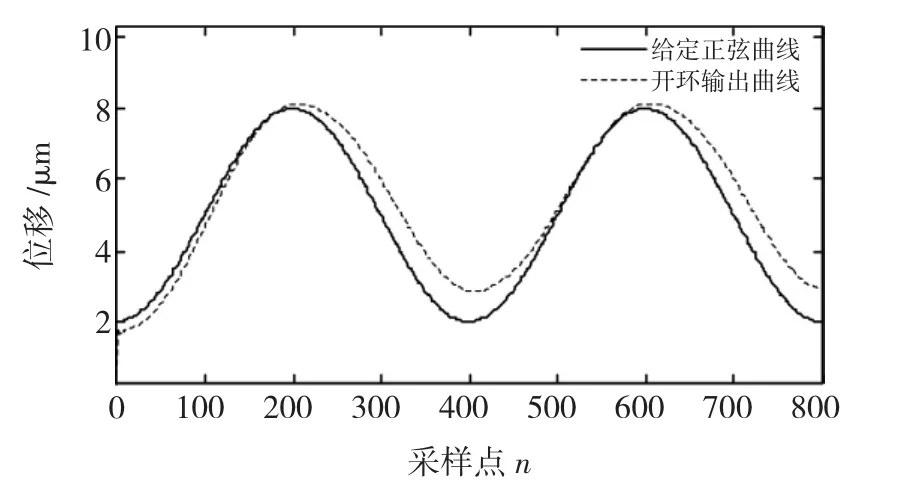
图5 开环控制跟踪曲线Fig．5 The tracking curve of open-loop control

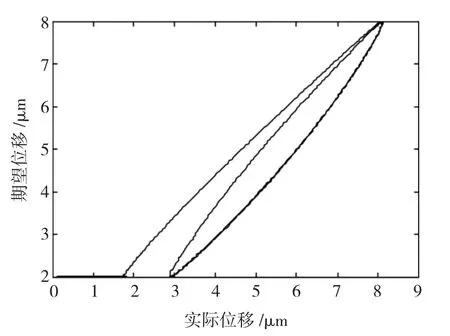
图6 开环控制拟合曲线Fig．6 The fitting curve

由开环实验可知，迟滞非线性所引起的扰动较大，所以对于普通滑模控制，其开关切换增益较大，由此产生的抖振也较大。如图7所示为跟踪正弦时候的抖振情况。

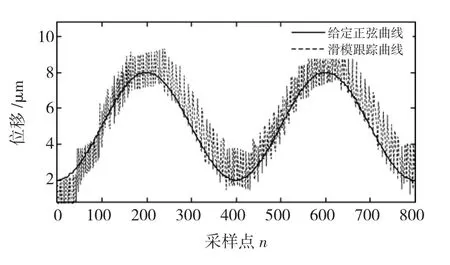
图7 普通滑模控制跟踪曲线Fig．7 Tacking curve of the conventional TVSMC

图8～图11为改进的多模时变滑模控制实验结果。其中，图8是固定设置一个积分切换点的实验情况，图中明显可以看到切换的过程的抖动。应用模糊理论确定切换时间后，积分的切换可以比较顺滑，如图9所示。图10为改进多模时变滑模控制的误差，其中，平均绝对值误差为0.013 5 μm，均方差为0.000 141。图11为实际输出与期望输出的拟合图，与图6相比，迟滞环被大部分抵消。

图8 固定切换时间的多模控制Fig．8 Multi-mode control of switching time fixed

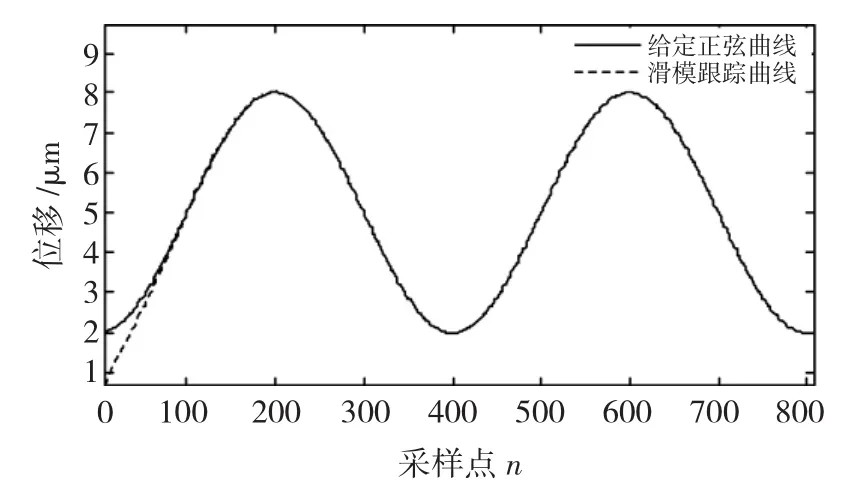
图9 模糊切换时间的多模控制Fig．9 Multi-mode control of switching time controlled by fuzzy controller

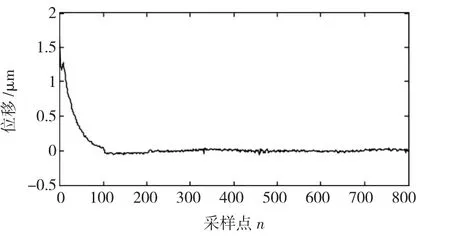
图10 误差曲线Fig．10 The error curve

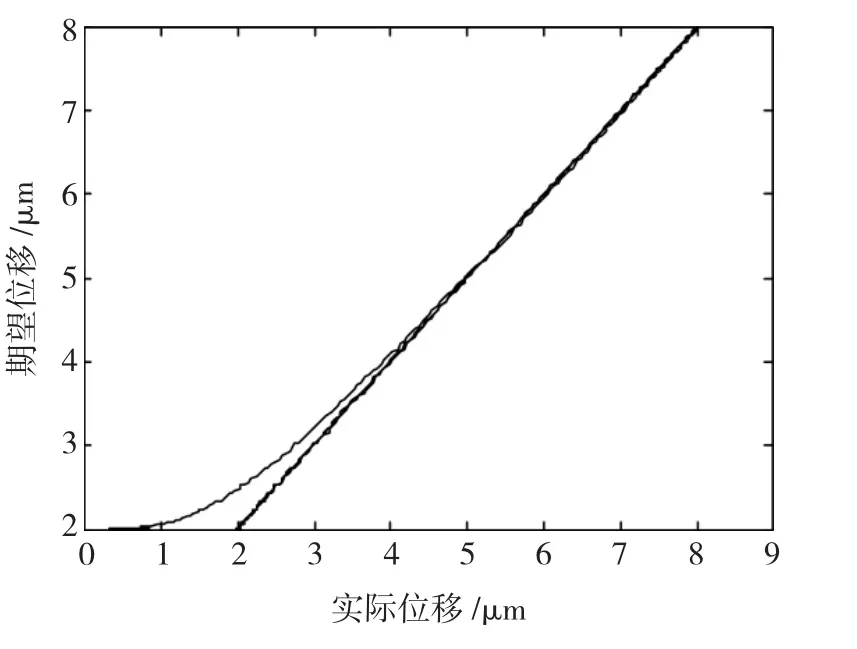
图11 拟合图Fig．11 The fitting curve

4 结论

为了提高压电陶瓷的控制精确度，提出了多模时变滑模逆补偿控制策略。针对迟滞非线性，在利用逆模型对迟滞进行串级补偿的基础上，对未能补偿的迟滞及蠕变等非线性，设计了时变滑模控制器。由于分别对达到阶段和稳态设计了两个滑模面，所以采用了多模控制。并且对切入时间用模糊控制得到。在消除滑模抖振方面，直接用滑模面代替切换函数，并且证明了其稳定性。实验结果验证了以上控制策略的有效性。

［1］VASILJEV P，MAZEIKA D，KULVIETIS G．Modelling and analysis of omni-directional piezoelectric actuator［J］．Journal of Sound and Vibration，2007，308(3/4/5):867－878．

［2］张栋，张承进，魏强．压电微动工作台的动态迟滞模型［J］．光学精密工程，2009，17(3):551－556．

ZHANG Dong，ZHANG Chengjin，WEI Qiang．Dynamic hysteresis model of piezopositioning stage［J］．Optics and Precision Engineering，2009，17(3):551－556．

［3］P．Ge，M．Jouaneh．Tracking control of a piezoceramic actuator［J］．IEEE Translations on Control System Technology，1996，4(3):209－216．

［4］J．C．Shen，W．Y．Jywe，H．K．Chiang，et al．Precision tracking control of a piezoelectric-actuated system［J］．Precision Engineering，2008，32(2):71－78．

［5］党选举．压电陶瓷执行器的神经网络实时自适应逆控制［J］．光学精密工程，2008，16(7):1266－1272．

DANG Xuanju．Real-time adaptive inverse control based on neural networks for piezoceramic actuator［J］．Precision Engineering，2008，16(7):1266－1272．

［6］王希花，郭书祥，叶秀芬，等．压电陶瓷迟滞特性的建模及复合控制［J］．电机与控制学报，2009，13(5):766－771．

WANG Xihua，GUO Shuxiang，YE Xiufen，et al．Modeling and feed-forward control based on piezoelectric ceramic hysteretic［J］．Electric Machines and Control，2009，13(5):766 －771．

［7］孙宝元．现代执行器技术［M］．长春:吉林大学出版社，2003:87－90．

［8］Jia-Tzer，Hsu and Khai D．T．Ngo．A hammerstein-based dynamic model for hysteresis phenomenon［J］．IEEE Transactions on Power Electronics，1997，12(3):406 －413．

［9］LAI Zhilin，LIU Xiangdong，CONG Binglong，et al．Time-varying sliding mode control in hysteresis compensation of the piezoceramic actuators based on the inverse preisach model［C］//2011 International Conference on Future Computer Science and Education，Xi'an，China．2011:553－557．

［10］CONG Binglong，LIU Xiangdong，CHEN Zhen．Exponential timevarying sliding mode control for large angle attitude eigenaxis maneuver of rigid spacecraft［J］．Chinese Journal of Aeronautics，2010，(23):447 －453．