电磁电动式磁悬浮装置的磁场分析和力特性研究

秦伟， 范瑜， 李硕， 吕刚， 朱熙

(北京交通大学电气工程学院，北京 100044)

0 引言

磁悬浮列车是一种新型地面无接触高速交通运输工具，其具有无噪音，无有害的废气，有利于环境保护;可节省建设经费;运营、维护和耗能费用低等特点，目前国际上研究的磁悬浮分为:电磁式磁悬浮和电动式磁悬浮。电动式悬浮装置是通过次级导体中感应出的涡流磁场相互作用产生悬浮力，相对于其它形式的磁悬浮列车更有独到之处:结构简单、悬浮气隙大，造价低，同时它并不需要复杂的闭环控制，因此将是磁悬浮发展的重要方向之一［1-4］。

目前研究的电动式磁悬浮系统主要是永磁电动式磁悬浮方案，其中以日本九州大学藤井教授提出的立式永磁磁轮方案［5］和美国威斯康星大学的Lipo教授提出的卧式磁轮方案［6］为代表的永磁磁轮方案均处于实验室研究阶段，永磁电动式磁悬浮要求永磁体与轨道之间存在相对运动才能实现悬浮，因此会产生附加的机械损耗，机械振动和陀螺仪效应，同时存在永磁体安装问题和掉落危险。

本文从电磁场分析出发，利用盘式电机分环计算理论对其内部的电磁关系进行解析计算，可以直接计算其力特性。悬浮力使用电磁场解析计算得到，这种方法避免了使用有限元得到法向磁密的复杂性和计算量大等缺点，完全使用解析方法解决，适合工程计算。通过得到的完全等效电路不仅可以得到推力、悬浮力等电机特性曲线，还可以为以后实现高性能的控制效果打下基础。

1 旋转磁场电动式磁悬浮装置

本文提出了旋转磁场电动式磁悬浮装置方案，该方案结构见图1，在盘式开槽铁心上对称放置线圈绕组，其工作原理是初级铁心中的三相绕组在气隙中产生旋转磁场，与次级导体中感应出的涡流磁场相互作用产生悬浮力，该方案具有以下优点:

1)本文提出的电动式磁悬浮方案属于固有的稳定系统，不需要复杂的控制系统也能维持悬浮状态，避免了电磁式磁悬浮控制策略复杂的缺点［1］;

2)初级铁心在静止情况下，绕组产生的旋转磁场能够产生悬浮力，避免了以日本超导磁悬浮为代表的一类电动式磁悬浮技术在静止时不产生悬浮力，需要支承的问题，同时避免了永磁体高速旋转产生的陀螺仪效应和永磁体脱落的危险。

该装置结构与单边铝次级盘式电机类似，其绕组沿铁心径向放置，在气隙中产生轴向磁通。这样的特殊结构导致磁路长度、齿宽、等效气隙长度以及磁路的饱和程度均随半径的增加而变化，使气隙磁场沿径向分布不均匀［6-8］。

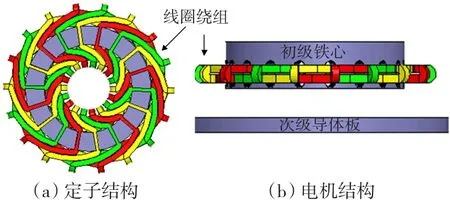
图1 装置示意图Fig．1 Rotation field electro-dynamic levitation device

2 电机的电磁模型分析

2.1 装置电磁模型

本文建立了电机的二维数学模型，将盘式悬浮装置沿径向等分为i个环如图2(a)，对每个环进行磁场分析，将各环沿径向切开拉直如图2(b)，对各环分别建立如图3所示坐标系，定义坐标y轴为次级导体板的上表面，区域1为初级铁心，区域3为次级导体板，区域2和4分别为初、次级之间的气隙及次级之后的气隙。各环分别采用其平均极距计算，其余参数如槽宽、铁心高度等均相等;假设纵向长度无穷大;由于次级面积大于初级，可假设次级宽度无穷大。

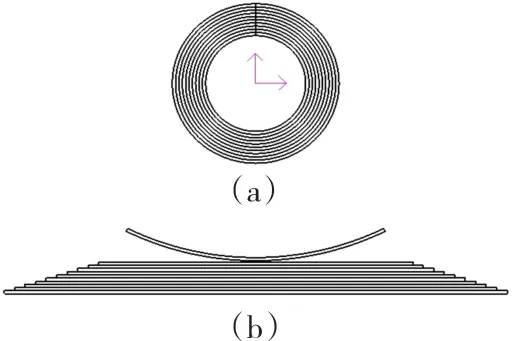
图2 电机分环示意图Fig．2 Sub-loop model of disc motor

图3 侧面展开图与求解坐标系Fig．3 Side elevation and coordinate system

初级绕组中的电流在初级表面形成的等效行波电流层为

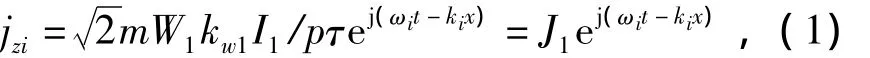
式中:m为初级绕组相数;W1为初级绕组匝数;kw1为初级绕组系数;I1为初级相电流有效值;p为绕组极对数;τi为第i环的平均极距;ωn为初级电流频率;系数ki=π/τi。

2.2 装置电磁场分析

假设初、次级之间无水平相对运动，初级绕组电流均沿z方向流动且三相电流对称［9-13］。

由于模型中各部分无水平运动，故初级磁场水平方向同步速率为初级电流基波频率ω，多层模型各层滑差率sn=1。则电磁波在多层模型中各区域的透入深度为

其中n=1，2，3，…为多层模型中的区域编号。

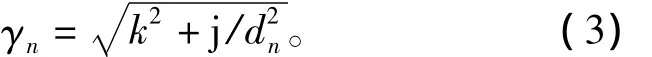
可以推导得出区域n下表面磁感应强度法向分量和磁场强度切向分量为

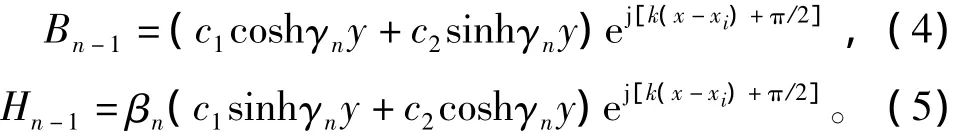
其中 βn=γn/(jkμn)

同样，在区域n上表面Bn，Hn可表示为

其中Dn为区域n厚度，则上下两表面的场量间存在的关系为

其中Tn称为区域n的转移矩阵。

对位于模型最上层的初级铁心区域—区域1，在厚度D0达到某一足够大的值时，B0趋近于1，则存在

在位于模型最上层的第二气隙区域4，由于在无穷远处B4=0，则可以得出

由于在分界面1存在表面电流层，对式(10)做出相应修正，即

求解式(9)～式(12)构成的方程组即可得到装置内部的磁场分布如图4所示。

图4 沿圆周方向气隙磁密分布Fig．4 Air-gap flux density along circumference

3 特性分析

3.1 悬浮力特性

样机初级固定，次级悬浮，其悬浮力Flr可采用麦克斯韦张量计算。

其中r2、r1分别为初级铁心的内外环半径。

图5是在气隙为2 mm，悬浮力和频率之间的关系，由图中可知随着频率的增加悬浮力呈线性增加，悬浮力和转差频率成单调上升关系，但频率上升至100 Hz左右之后，悬浮力随转差频率的提高并不明显，电磁损耗却会不断加剧，故该装置应用中应综合考虑，选择效率较高的工作频率。

图5 悬浮力与频率在不同相电流下的曲线Fig．5 Curve between lift force and frequency with different current

从图6可以看出，随着气隙的增加悬浮力呈现减小的趋势，比较2 mm和5 mm，5 mm和10 mm之间的差量可以看出随着气隙的增加悬浮力的减小速度将放缓。

图7的曲线是初级电流频率50 Hz，气隙长度2 mm条件下求得的悬浮力和初级电流之间的关系，可见悬浮力随初级相电流幅值的增长呈平方正比的关系上升，因此增加初级电流幅值是提高悬浮力的重要手段，在条件容许的情况下应考虑应用超导技术。

图6 悬浮力与频率在不同气隙下的曲线Fig．6 Curve between lift force and frequency with different air-gap

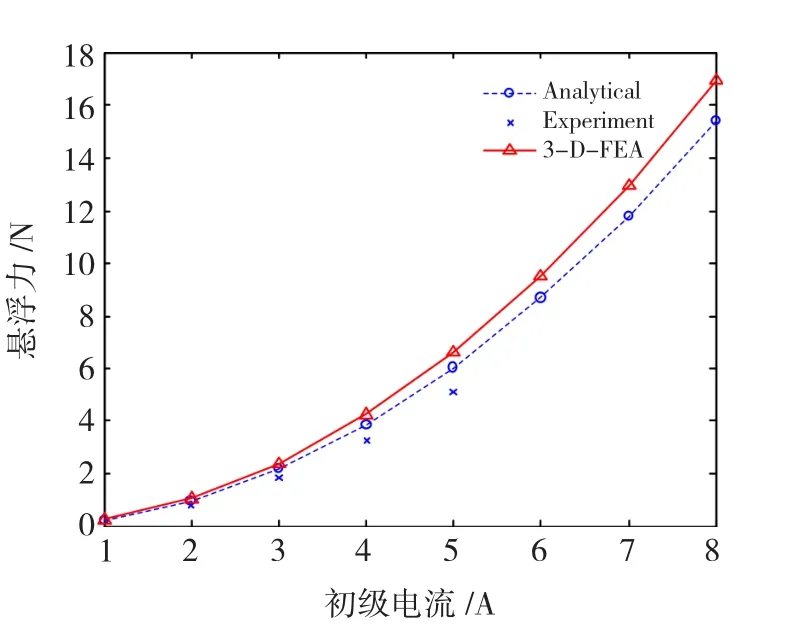
图7 悬浮力与电流幅值关系曲线Fig．7 Curve between lift force and primary phase current

3.2 水平转矩特性

该装置在产生竖直方向上的悬浮力的同时也存在水平转矩，为了克服自旋转矩本文的悬浮装置在实际应用中均为采用气隙磁场互为反方向旋转“成对”使用，但装置的水平转矩会对装置的结构稳定性造成隐患，因此需要对水平转矩进行分析计算，通过磁场储能和虚位移法计算得到转矩［14］。

图8是在气隙为2 mm，水平转矩和频率之间的关系，由图中可知随着频率的增加水平先增加后减小，结合图5和图6可知悬浮力在100 Hz出现饱和而水平转矩100 Hz已经出现递减趋势，因此效率较高的工作频率应该在100 Hz左右。

水平转矩与频率关系曲线如图9所示。图10是在初级相电流为3 A时求得的水平转矩与气隙长度之间的关系曲线，由图9和图10可知水平转矩随气隙长度增加呈单调下降并随着气隙的增加下降趋势减缓。

为了验证解析计算和有限元计算的正确性，建立了如图11所示的旋转磁场电动式磁悬浮装置样机实验平台，本装置优点是初级下气隙均匀，次级铝板使用可以调节的螺栓与拉压传感器相连，可以通过调节螺栓做出任意次级厚度，和任意气隙大小的实验。样机初级铁心内、外径分别为60 mm、100 mm，铁心高25 mm，初级绕组采用4极单层链式绕组，每相匝数800，次级导体板为2～5 mm厚铝板［15］。使用其对理论计算值进行了实验验证，实验结果体现在图7、图10之中，与理论计算结果趋势吻合，证明理论分析结论是真实可信的。

图8 水平转矩与频率关系曲线Fig．8 Curve between torque and frequency

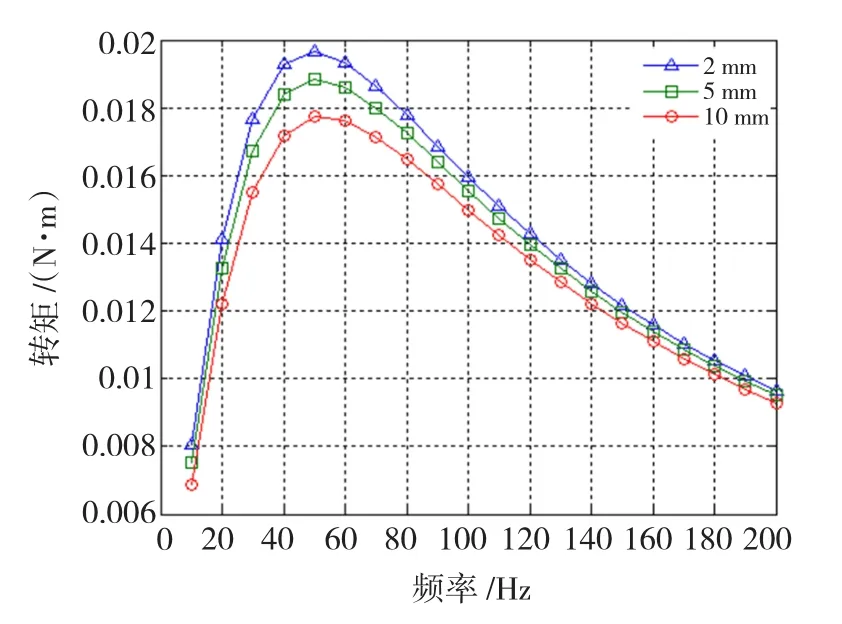
图9 水平转矩与频率关系曲线Fig．9 Curve between torque and frequency

图10 水平转矩与气隙长度关系曲线Fig．10 Curve between torque and air-gap length

图11 旋转磁场电动式磁悬浮装置样机Fig．11 Rotation field electro-dynamic levitation device prototype

4 结论

1)本文提出的旋转磁场电动式磁悬浮系统在一定的电流幅值和频率能够产生足够的悬浮力，实现稳定的电动式磁悬浮。本文使用解析方法和有限元法得到了导体板和气隙的磁场分布，推导计算悬浮力和水平转矩，为旋转磁场电动式磁悬浮系统的特性分析和设计提供了参考。

2)该装置产生稳定悬浮力的同时会产生较大的自旋转矩，因此在实际应用中应“成对”出现抵消水平自旋转据。

3)该装置的悬浮性能仍存在较大的提升空间，如采用超导线圈，提高气隙磁密，增大悬浮力，提高装置的整体效率。

［1］YAN Luguang.Development and application of the magnet technology in China［C］//Proceedings of Fifteenth International Conference on Magnet Technology，October 20-24，1997，Beijing，China.1997:30-35.

［2］秦伟，范瑜，朱熙，等.永磁电动式磁悬浮装置的研究［J］.电机与控制学报，2011，15(7):77-81.

QIN Wei，FAN Yu，ZHU Xi，et al.Analysis of permanent-magnet electro-dynamic maglev device［J］.Electric Machines and Control，2011，15(7):77-81.

［3］NEHL T W，LEQUESNE B，GANGLA V，et al.Nonlinear twodimensional finite element modeling of permanent magnet eddy current couplings and brakes［J］.IEEE Transactions on Magnetics，1994，30(5):3000-3003.

［4］秦伟，范瑜，吕刚，等.非磁性次级感应悬浮电机磁场和力特性研究［J］. 电机与控制学报，2011，15(8):1-6.

QIN Wei，FAN Yu，LÜ Gang，et al.Characteristic and magnetic field analysis non-magnetic secondary induction maglev motor［J］.Electric Machines and Control，2011，15(8):1-6.

［5］FUJII Nobuo，CHIDA Makoto，OGAWA Kokichi.Three dimensional force of magnet wheel with revolving permanent magnets［J］.IEEE Transactions on Magnets，1997，30(5):4221-4223.

［6］BIRD Jonathan.An investigation into the use of electrodynamic wheels for high speed ground transportation［D］.Wisconsin:U-niversity of Wisconsin，2007.

［7］孙建忠，白凤仙.特种电机及其控制［M］.北京:中国水利水电出版社，2005:155-198.

［8］王琳，何全普，马志云.轴向磁场异步电机磁场分布研究——兼评某些量的工程计算方法［J］.电工技术杂志，1992(3):6-8.

WANG Lin，HE Quanpu，MA Zhiyun.Investigation on magnetic field distribution of axial field induction motor——engineering calculation method of some parameters［J］.Electric Engineering，1992(3):6-8.

［9］关恩禄，关沫.三相盘式感应电机设计要点及优化设计［J］.沈阳工业大学学报，1999，21(6):502-505.

GUAN Enlu，GUAN Mo.Design point of three-phase disc induction motor and optimization design［J］.Journal of Shenyang University of Technology，1999，21(6):502-505.

［10］龙遐令.直线感应电动机的理论和电磁设计方法［M］.北京:科学出版社，2006:1-156.

［11］NASAR S A，BOLDEA I.Linear motion electric machines［M］.New York:John Wiley ＆ Sons Inc，1976:57-137.

［12］G Qishan，H Shuhong.Analytic approach to magnetic circuit for saturated axial-field induction machines［J］.IEE Proceedings-E-lectric Power Applications，1994，141(1):27-32.

［13］唐孝镐，宁玉泉，傅丰礼.实心转子异步电机及其应用［M］.北京:机械工业出版社，1991:1-191.

［14］辜承林.次级无铁心式直流永磁盘式电机的磁场和解析解分析与优化设计［J］.中国电机工程学报，1996，16(2):125-129.

GU Chenglin.Optimization of permanent-magnet axial field coreless DC motors based on magnetic-field-magnet method［J］.Proceedings of the CSEE，1996，16(2):125-129.

［15］朱熙，范瑜，吕刚，等.单边盘式感应电机的数学模型与转矩分析［J］. 中国电机工程学报，2010，30(24):69-74.

ZHU Xi，FAN Yu，LÜ Gang，et al.Modeling and torque analysis of a disc induction motro［J］.Proceedings of the CSEE，2010，30(24):69-74.