车用永磁同步电机的改进MTPA控制策略研究

廖勇， 伍泽东， 刘刃

(重庆大学输配电装备及系统安全与新技术国家重点实验室，重庆 400030)

0 引言

内置式永磁同步电机(interior permanent magnet synchronous motors，IPMSM)以其高效率、高功率密度、低噪声、高转矩电流比、强鲁棒性［1］等优点，在电动车驱动控制系统中得到了广泛的应用。针对IPMSM交直轴电感不相等的特性，为了最大限度利用IPMSM的磁阻转矩，目前车用永磁同步电机系统均采用最大转矩电流比(MTPA)的控制策略，即利用最小的定子电流获得最大的电磁转矩输出。

鉴于最大转矩电流比控制的优点，不少学者对IPMSM的最大转矩电流比控制进行了大量的研究。文献［2］提出了一种便于工程实际应用的MTPA控制策略，该策略采用拉格朗日乘子法，利用迭代法求取最大转矩下的d－q轴电流的表达式;文献［3］提出将自抗扰控制与MTPA控制策略相结合的控制方法，以改善系统的动态特性和调节特性，但上述方法是基于电机模型的准确电机参数，参数误差大将导致控制困难和系统性能下降。为了提高系统的控制性能，获得准确的电机参数成了人们研究的热点，进而提出了许多电机的参数辨识方法［1，4－10］。此外，还有很多学者采用自适应控制［11－12］、卡尔曼滤波器［13］、遗传算法［14］等先进的控制方法来估算电机参数。由于以上算法非常复杂，难于工程实现，文献［15］针对上述算法的不足，提出了利用搜索法来实现最大转矩电流比的控制策略，该方法避免了系统控制性能对电机参数的严重依赖。但是该搜索法设定的搜索初值为90°转矩角，使得搜索速度慢;并且采用定步长搜索，搜索结果将在最优转矩角附近振荡，造成转矩振荡，搜索精确度差。

本文针对上述算法的不足，提出了一种改进的MTPA控制算法，将IPMSM转矩角的复杂公式进行多项式拟合，利用拟合的多项式近似求取转矩角，并将该转矩角作为初始值进行变步长搜索，该算法避开了电机参数的影响，并且搜索速度快，搜索精度高，能够实现最优的控制效果。

1 永磁同步电机MTPA控制原理

最大转矩电流比控制，又称为定子电流最小控制，即在给定转矩的情况下，最优配置交直轴电流分量，使定子电流最小，达到单位电流下电机输出转矩最大。最大转矩电流比控制可以减小电机铜耗，提高运行效率，从而使整个系统的控制得到优化。另外，对电动车驱动系统，逆变器的容量是一定的，采用最大转矩电流比控制，可以使逆变器所需输出电流较小，逆变器的功率等级要求可相对降低。

采用恒功率变换得到电机在d－q轴坐标系下(以同步速度旋转且q轴超前于d轴90ο电角度)的IPMSM的电压方程为［1］

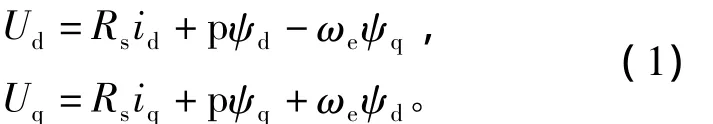
d－q轴系磁链方程为

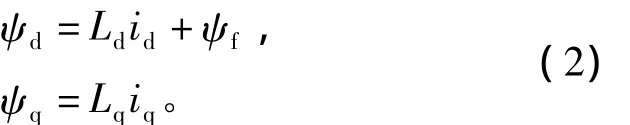
电磁转矩方程为

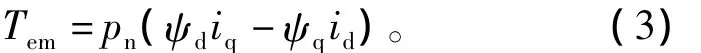
其中:p 为微分算子;Ud、Uq、id、iq为 d、q 轴电压和电流;Rs为定子电阻;Ld、Lq为 d、q 轴电感;ψd、ψq为d、q轴磁链;ψf为永磁体磁链;ωe为电角速度;pn为电机极对数;Tem为电磁转矩。

在d－q轴坐标系下，d、q轴电流分量 id、iq可以用定子电流is和转矩角β表示，即

将式(2)和式(4)代入式(3)，可得到新的电磁转矩表达式，即

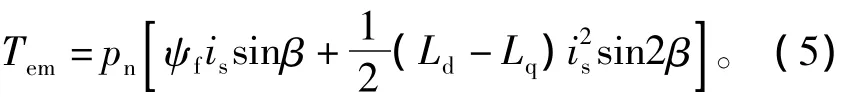
如上式所示，在定子电流is的一定的条件下，不同的转矩角β，对应不同的电磁转矩。通过对式(5)求极值，可得到满足转矩电流比最大的最优转矩角表达式，即

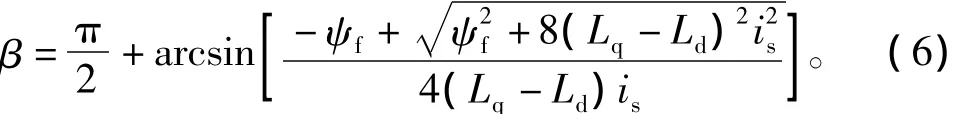
通过对电机电磁功率表达式(6)的分析，可知最大转矩电流比控制的核心在于:在定子电流一定的条件下，如何求得最优转矩角，从而实现输出电磁转矩最大。

传统的IPMSM最大转矩电流比控制策略，即是采用式(6)来求的最优转矩角β，并且可以看出，转矩角的求取非常复杂，需要进行开方和反正弦运算，而且严格依赖于电机的电感以及永磁体磁链参数，然而这些参数随着电机运行的工况不同会发生较大变化，会对转矩角的计算带来较大的误差，影响系统的控制性能。为了克服传统方法的不足，搜索法在MTPA控制中得到了应用，但现有搜索法采用定步长搜索，该搜索法得到的转矩角在最优转矩角附近震荡，造成控制电流振荡，最终使电磁转矩振荡，精确度较差;而且该算法以90°转矩角为初始值开始启动搜索，系统响应时间慢。

2 改进的MTPA控制策略

基于以上所述控制策略的不足，提出将IPMSM转矩角的复杂公式进行多项式拟合，利用拟合的多项式近似求取转矩角，并将该转矩角作为初始值进行变步长搜索的永磁同步电机改进MTPA控制方法。

由于理论转矩角计算复杂，考虑到工程实际中运算的可行性，采用二阶多项式拟合方法得到的转矩角表达式为

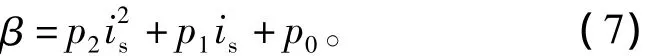
式中，p0、p1、p2是在电机参数一定的情况下，利用最小二乘法得到的2阶多项式的各阶系数。

利用拟合公式计算的转矩角，由于电机参数的不准确性以及拟合本身存在的固有误差会使得该转矩角β偏离最优点，为寻找到最优转矩角，提出变步长的搜索方法，该搜索法的离散计算公式表达为

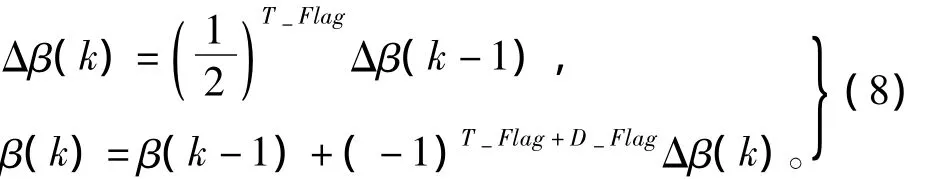
式中:Δβ为搜索步长;T－Flag为转矩变化标志，等于0表示转矩增大，等于1表示转矩减小;D－Flag为搜索方向标志，等于0时表示搜索方向是正方向，等于1表示搜索方向为反方向。T－Flag的具体确定原则为

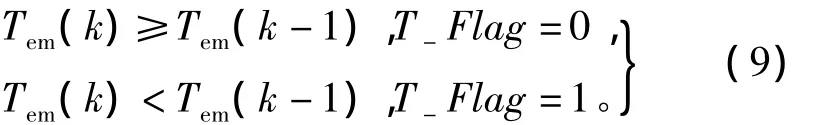
式中，Tem(k－1)、Tem(k)分别表示前后两次电机的电磁转矩值。T－Flag的确定只与前后两次转矩的大小有关。

D－Flag的具体确定原则为:

①T－Flag=0且D－Flag=0，重新设定D－Flag=0;

②T－Flag=0且D－Flag=1，重新设定D－Flag=1;

③T－Flag=1且D－Flag=0，重新设定D－Flag=1;

④T－Flag=1且D－Flag=1，重新设定D－Flag=0。

由上面的确定原则可以看出，D－Flag的确定不仅与T－Flag有关，而且也与前一次的设定的搜索方向有关。T－Flag与D－Flag的不同组合确定了下一次搜索的方向，即设定D－Flag的值。

式(9)中T－Flag的确定需要比较前后两次的电磁转矩值，这就需要计算电磁转矩Tem。在稳态情况下，式(1)可以表述为

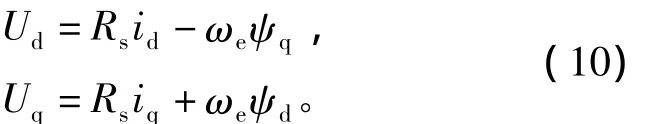
由上式可以得到磁链计算的表达式为

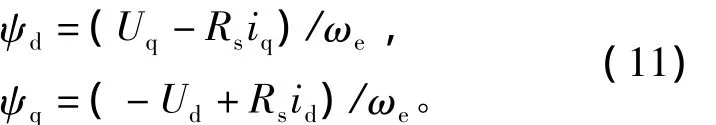
将上式所述磁链表达式代入式(3)，得到新的转矩表达式为

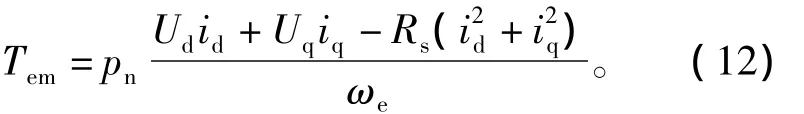
式中:id、iq为电机实测三相电流经过坐标变换后得到的d－q轴电流。ωe为实际测得的电机电角速度。Ud、Uq为输出到逆变器的控制电压。这样，电磁转矩的计算就仅受电机定子电阻Rs的影响，但车用IPMSM的定子电阻Rs非常小，可以忽略电阻的变化带来的影响，因此采用式(12)来计算电机的电磁转矩是相对准确的。

通过以上分析，车用永磁同步电机改进的MTPA控制策略其具体的算法流程如图1所示。

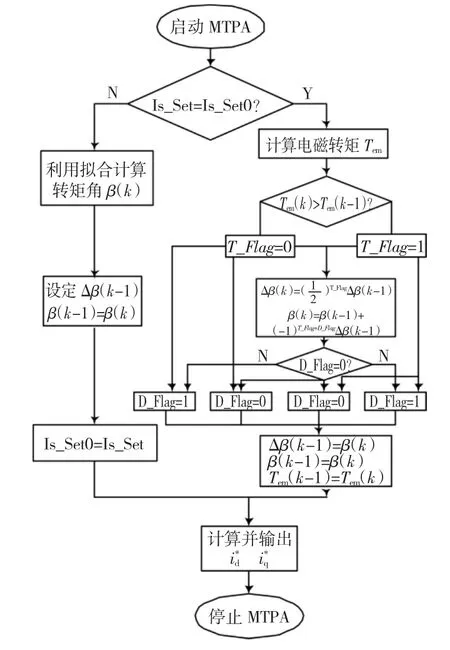
图1 改进的MTPA控制算法流程图Fig．1 Flowchart of improved MTPA control algorithm

如上图所示，首先判断给定的is是否发生突变，如果发生突变，则通过拟合的二次多项式求取最新的转矩角β。此时的转矩角偏离最优点，进入变步长搜索算法，通过设定的搜索方向进行搜索，判断电磁转矩是否增大，如果是增大的，搜索方向正确，搜索步长Δβ不变，继续正向增大转矩角，当增大到一定的转矩角时，继续增大β，转矩角将超过最优点，使得电磁转矩会减小，此时改变搜索方向，同时将搜索步长减半，继续搜索，如此往复，转矩角β将快速的收敛于最优点，系统在给定的is条件下进入稳态，实现最优的最大转矩电流比控制。

将改进的控制策略应用于实际的车用永磁同步电机控制系统中，图2给出了整个控制系统的矢量控制框图。

如图2所示，在传统永磁同步电机矢量控制算法的基础上，增加了转矩计算单元，利用计算的转矩和给定的电流，寻找到最优的转矩角，然后根据转矩角算出给定的d－q轴电流，实现车用IPMSM的最 大转矩电流比控制。

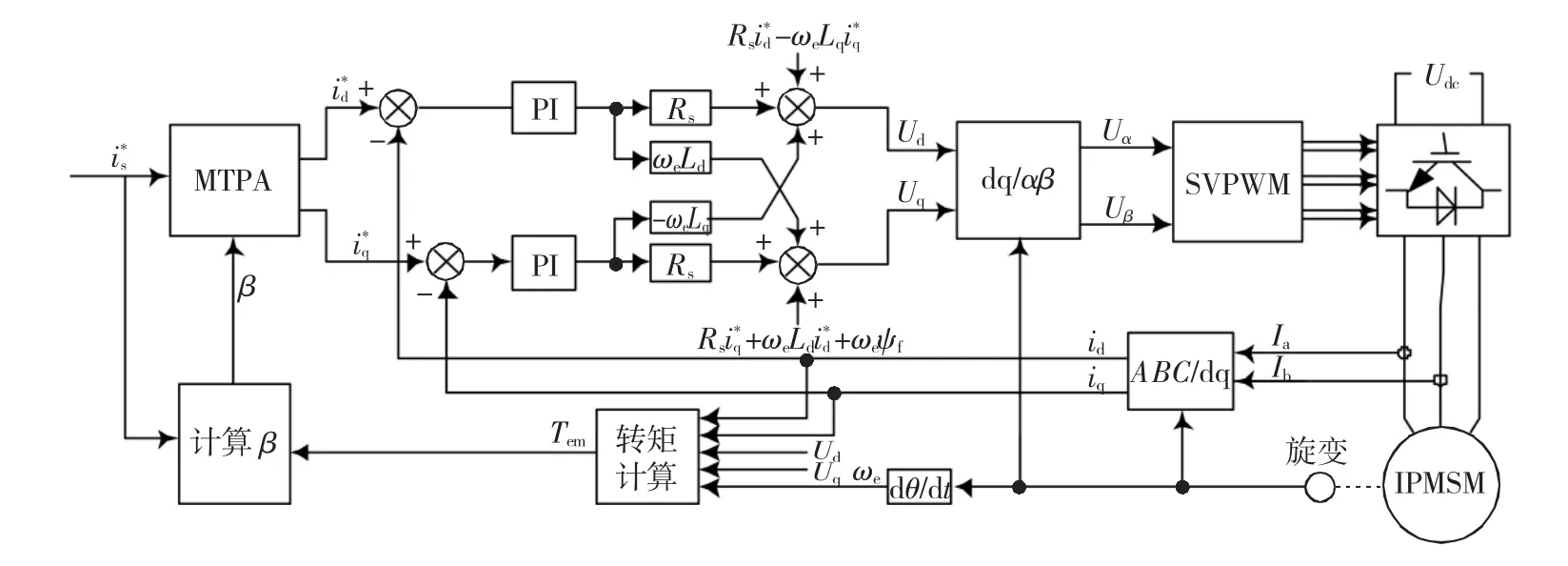
图2 改进MTPA矢量控制系统框图Fig．2 Block diagram improvement of MTPA vector control system

3 仿真结果及分析

针对上述方法，利用Matlab/SIMULINK建立了IPMSM的MTPA控制策略的仿真模型，仿真时选用的永磁同步电机参数:额定功率 P=30 kW，定子电阻Rs=0.021 21 Ω;d轴电感Ld=0.5 mH;q轴电感Lq=1.628 mH;永磁体磁链Ψf=0.196 8 Wb;极对数np=3;直流母线电压UDC=300 V。根据以上的电机参数，得到转矩角拟合多项式表达式为

图3给出了最大转矩电流比控制模式下，转矩角与定子电流的关系曲线，从图中可以看出，理论计算的曲线和拟合得到的曲线吻合较好。

图4 各种MTPA控制方法仿真波形Fig．4 A variety of MTPA control method simulation waveform

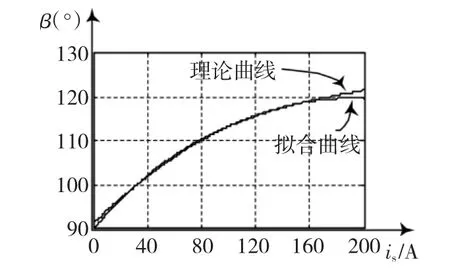
图3 转矩角与定子电流关系图Fig．3 Diagram angle of torque and stator current

系统仿真时间设定为6 s，系统初始电流给定为is=60 A，2 s时阶跃到90 A，4 s时阶跃到120 A，采用不同MTPA控制方法得到的仿真波形如图4所示。

图4(a)是采用传统的MTPA算法得到的仿真波形，即根据理论公式计算得到最优转矩角。由于该电机模型是理想的线性模型，电机参数是准确的，所以理论计算的转矩角就是最优转矩角;图4(b)采用传统的定步长搜索法得到的仿真波形，该方法能够得到最优转矩角，根据仿真波形分析可得，步长越长，搜索时间越快，但在稳定点附近的振荡就越大，反之，步长越小，在稳定点附近的振荡越小，精确度相对较高，但是搜索速度变慢;图4(c)是采用改进的MTPA控制方法得到的仿真波形，对比传统理论算法的仿真波形可知，该算法能够得到最优的转矩角。转矩角β从初始位置开始经过较快的调整后稳定，转矩角β搜索速度较快，电磁转矩平稳，脉动较小，控制精确度较高。

4 实验结果及分析

整个实验系统由控制驱动系统、车用电机、直流负载机以及动力电源等设备组成，以TI公司的DSP TMS320F2812为控制核心的永磁同步电动机控制系统，实验电机为车用永磁同步电动机，电机参数为:额定功率P=30 kW，定子电阻Rs=0.021 21 Ω;d轴电感Ld=0.5 mH;q轴电感Lq=1.628 mH;永磁体磁链Ψf=0.196 8 Wb;极对数np=3;直流母线电压UDC=300 V。功率器件采用Infineon公司的三相IGBT逆变桥(FS800R07A2E3)，电流检测采用了LEM的霍尔电流传感器LF505－S，电机的位置传感器采用旋转变压器，旋变的解码芯片为AD公司产品AD2S1210。

实验数据采用串口传输的方式以及示波器抓拍数据。由于转矩角要求的精确度比较高，转矩角数据采用串口将控制器的数据传送到上位机保存，而电流和转矩数据通过用D/A转换后输出，用示波器抓拍的方式保存数据。所有的数据都经过MATLAB软件重新绘制，如图5所示。

图5给出了定子电流在0 s时从is=0 A阶跃到is=20 A，在10 s阶跃到is=50 A的情况下，采用不同最大转矩电流比控制得到的实验波形，图5(a)是采用传统算法得到的电机转矩角、dq轴电流以及电磁转矩波形，图5(b)是采用改进的MTPA控制算法得到的电机转矩角、dq轴电流以及电磁转矩波形。从实验波形可以看出，在is=20 A的状态下，采用改进的MTPA算法搜索得到的转矩角为99.95°，比传统计算得到的96.42°增加了3.53°，电磁转矩值比传统算法得到的增加大约1.9 N·m;在is=50 A的情况下，改进的MTPA算法搜索得到的转矩角为109.2°，比传统算法得到的 104.5°增加了 4.7°，电磁转矩值增加了大约4.0 N·m。

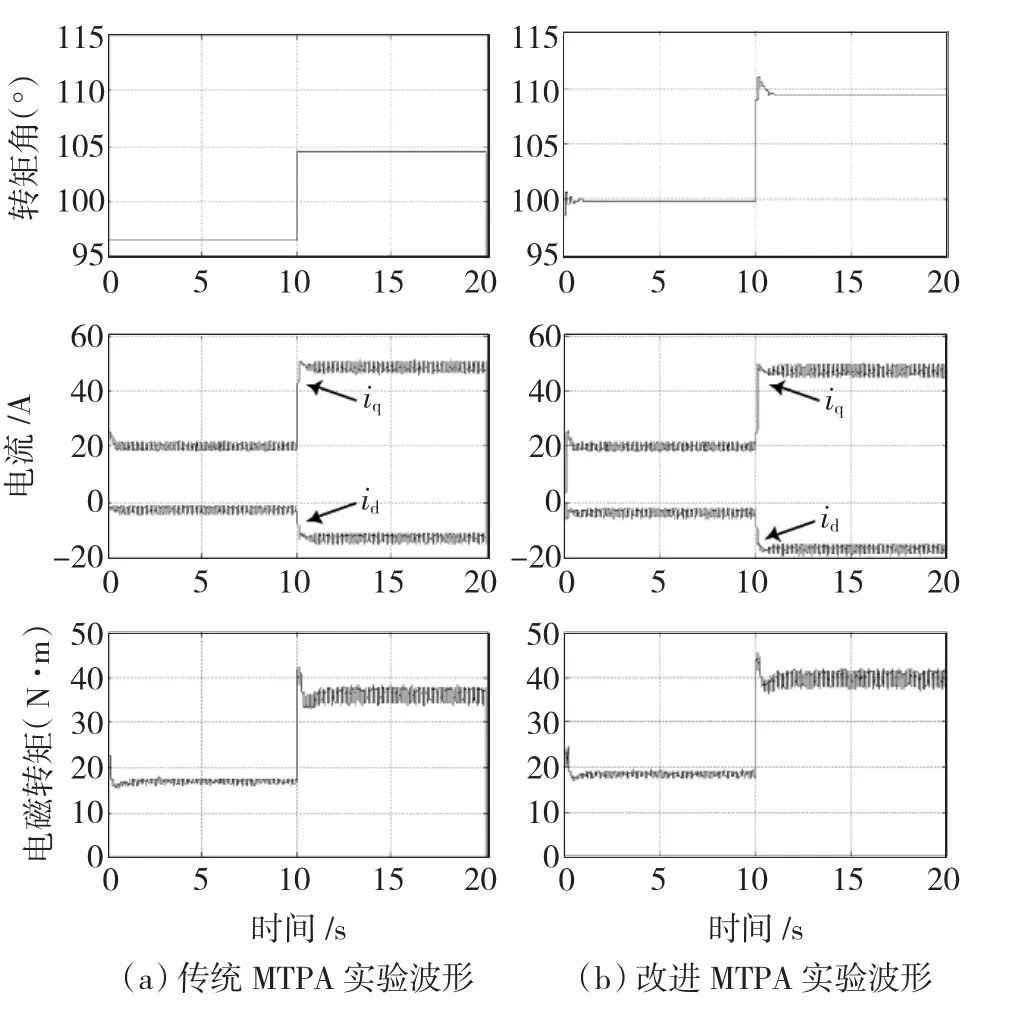
图5 两种MTPA控制方法的对比实验波形Fig．5 Two MTPA control method’s experimental waveforms

通过对比实验波形可知，改进的算法避开了电机参数的影响，在相同的定子电流下，电机输出更大的电磁转矩，系统的响应速度较快;对比文献［15］中采用传统搜索法的实验波形，可以看出，改进算法搜索速度快，最优转矩角无振荡，控制精确度较高。

5 结论

本文提出了一种改进的MTPA控制策略，利用变步长的思想，通过对电磁转矩的辨识搜索获取最优转矩角，实现最优控制。对提出的算法进行了仿真和实验研究，通过与传统理论方法与传统搜索算法相比，该改进算法避开了电机参数的影响;具有快速的收敛性和较高的控制精确度;而且算法实现简单，便于实际工程应用。

本文通过对转矩的辨识确定搜索的方向与步长，转矩辨识的精度制约了控制的性能的优劣。在低转速下，转矩的辨识误差较大，如何提高转矩辨识的精确度有待进一步研究。

［1］王成元，夏加宽，杨俊友，孙宜标．电机现代控制技术［M］．北京:机械工业出版社，2006:81－99．

［2］李长红，陈明俊，吴小役．PMSM调速系统中最大转矩电流比控制方法的研究［J］．中国电机工程学报，2005，25(21):169－174．LI Changhong，CHEN Mingjun，WU Xiaoyi．Study of a maximum ratio of torque to current control method for PMSM［J］．Proceeding of the CSEE，2005，25(21):169 －174．

［3］WEN Jianping，CAO Binggang．A robust MTPA controller for high efficiency IPM synchronous motor［J］．Intelligent Vehicles Symposium，2009:829－832．

［4］Yasser Abdel-Rady Ibrahim Mohamed，TsingK．Lee，Adaptive self-tuning MTPA vector controller for IPMSM drive system［J］．IEEE Transactions on Energy Conversion，2006，21(3):636－644．

［5］安群涛，孙力，赵克．一种永磁同步电动机参数的自适应在线辨识方法［J］．电工技术学报，2008，23(6):31 －36．

AN Quntao，SUN Li，ZHAO Ke．An adaptive on-line identification method for the parameters of permanent magnet synchronous motor［J］．Transactions of China Electro Technical Society，2008，23(6):31－36．

［6］Hyunbae Kim．Using on-line parameter estimation to improve efficiency of IPM machine drives［C］//IEEE 33rd Annual Power E-lectronics Specialists Conference(PESC)，June 23 －27，2002，Cairns，Australia．2002:815 －820．

［7］S．M．Fazeli，H．W．Ping，H．Abootorabi Zarchi．Robust maximum torque per ampere(MTPA)control of interior permanent magnet synchronous motor drives using adaptive input-output feedback linearization approach［C］//International Conference for Technical Postgraduates(TECHPOS)，Dec 14 － 15，2009，Kuala Lumpur，Malaysia，2010，2(17):1 －6．

［8］Silverio Bolognani，Roberto Petrella，Antonio Prearo，et al．Online tracking of the MTPA trajectory in IPM motors via active power measurement［C］//XIX International Conference on Electrical Machines(ICEM)，Sept 6 －8，2010，Padova，Italy．2010.10(25):1－7．

［9］Sungmin Kim，Young-Doo Yoon，Seung-Ki Sul，et al．Parameter Independent maximum torque per ampere(MTPA)control of IPM machine based on signal injection［C］//Twenty-Fifth Annual IEEE on Applied Power Electronics Conference and Exposition(APEC)，Feb 21 －25，2010，Seoul，South Korea．2010.3(18):21－25．

［10］Silverio Bolognani，Roberto Petrella，Antonio Prearo，et al．Automatic tracking of MTPA trajectory in IPM motor drives based on AC current injection［J］．IEEE Transactions on Industry Applications，2010.11(09):105 －114．

［11］陈振锋，钟彦儒，李洁．嵌入式永磁同步电机自适应在线参数辨识［J］．电机与控制学报，2010，14(4):9 －13．

CHEN Zhenfeng，ZHONG Yanru，LI Jie．Online adaptive parameter identification for interior permanent magnet synchronous motor drive［J］．Electric Machines and Control，2010，14(4):9－13．

［12］裘君，赵光宙．永磁同步电机磁链自适应控制［J］．电机与控制学报，2009，13(6):798 －803．

QIU Jun，ZHAO Guangzhou．Flux adaptive control for PMSM［J］．Electric Machines and Control，2009，13(6):798 －803．

［13］卢迪，刘明基，吴海涛．永磁同步电动机系统参数和状态的推广卡尔曼滤波估计［J］．电机与控制学报，2003，7(4):281－284．

LU Di，LIU Mingji，WU Haitao．Parameter and state estimation of PMSM system with extended Kalman filter［J］．Electric Machines and Control，2003，7(4):281 －284．

［14］吴茂林，黄声华．永磁同步电机非线性参数辨识［J］．电工技术学报，2009，24(8):65 －68．

WU Maolin，HUANG Shenghua．Nonlinear parameters identification of PMSM［J］．Transactions of China Electro Technical Society，2009，24(8):65 －68．

［15］Dianov Anton，Kim Young-Kwan，Lee Sang-Joon，et al．Robust self-tuning MTPA algorithm for IPMSM drives［C］//Industrial E-lectronics 2008，34th Annual Conference of IEEE，Nov 10－13，2008，Suwon，South Korea，2008:1355 －1360．