基于自适应强跟踪滤波器的汽车行驶状态软测量

周聪， 肖建

(西南交通大学电气工程学院，四川成都 610031)

0 引言

现代汽车应用越来越多的电子控制系统来提高汽车的安全性、稳定性以及驾驶舒适性。电子稳定程序(electronic stability program，ESP)、四轮转向控制(four wheel steering，4WS)、主动转向控制(active steering control，ASC)等通过控制车身的侧向和横摆运动来提高汽车的操纵稳定性;主动侧倾控制(active roll control，ARC)、主动车身控制系统(active body control，ABC)等通过控制车身的垂直、倾覆运动来改善汽车的驾驶舒适性。要实现这些电子控制系统的特定功能，前提条件就是要准确获得汽车行驶过程中的状态参数，如纵向车速、侧向加速度、横摆角速度、质心侧偏角等。

由于测量技术和测量成本的原因，要直接测量所有重要的状态变量存在一定难度。目前，基于状态估计的软测量技术已被成功应用于估计汽车的动力学和运动学参数信息。Venhovens［1］和 Gustaffson［2］等采用卡尔曼滤波器(Kalman filter，KF)估计汽车的侧向加速度、横摆角速度、轮胎力和路胎摩擦系数;Wenzel［3-4］等采用双扩展卡尔曼滤波器(dual extended Kalman filter，DEKF)并行估计车辆的状态变量和参数变量;另外，也有一部分学者采用龙贝格观测器和滑模观测器估计汽车的质心侧偏角和侧向力［5-7］。

在这些估计算法中，基于KF的状态估计方法应用最为广泛，在实车试验中也取得了较好的效果。但是KF算法的设计难点为:1)要求精确知道被观测系统的模型;2)要求已知系统噪声和测量噪声的统计特性。因此，要提高KF算法的估计效果，必须同时从模型和测量两个方面着手。Sage-Husa自适应卡尔曼滤波通过引入虚拟噪声补偿系统的未建模动态，提高了滤波算法的精确度和鲁棒性［8］。强跟踪滤波器(strong track filter，STF)采用多重渐消因子有效地削弱了以往数据对模型误差的影响，具有准确跟踪状态突变的能力［9］。本文以3自由度非线性汽车动力学模型为基础，将自适应卡尔曼滤波器和STF算法相融合，提出一种基于自适应强跟踪滤波(adaptive strong track filter，ASTF)的汽车行驶状态估计算法，用于汽车的行驶状态变量的软测量中。该方法有效克服由于汽车动力学模型中的未建模动态引起的估计误差过大和行驶过程中突变状态的跟随问题。在此基础上，通过Carsim和Matlab/SIMULINK联合仿真，分别运用ASTF和EKF对车辆的纵向车速、横摆角速度及质心侧偏角等关键状态进行实时估计。

1 汽车的非线性动力学模型

用于分析汽车横摆和侧向运动的2自由度模型是一个假设汽车以匀速行驶的线性模型。但在实际当中，纵向车速是随时可能发生变化的，而变化的纵向车速对汽车的横摆和侧向运动有显著的影响，且构成状态变量之间的非线性关系。本文以横摆、侧向、纵向3自由度非线性汽车动力学模型为基础，构建汽车状态估计的软测量模型。图1为3自由度汽车动力学模型。

图1 3自由度汽车动力学模型Fig．1 3 DOF vehicle dynamic model

如图1所示，XaOaYa为固定在水平面上的绝对坐标系，xoy为固定在汽车质心上的车辆坐标系。其中，x轴与汽车的纵向对称轴重合，规定向前为正;y轴通过车辆的质心o点，规定向左为正;所有XaOaYa平面内的角度和力矩以逆时针方向为正，各矢量的分量以与坐标轴通向为正。该3自由度非线性汽车动力学模型的状态方程和观测方程如式(1)、式(2)所示，即

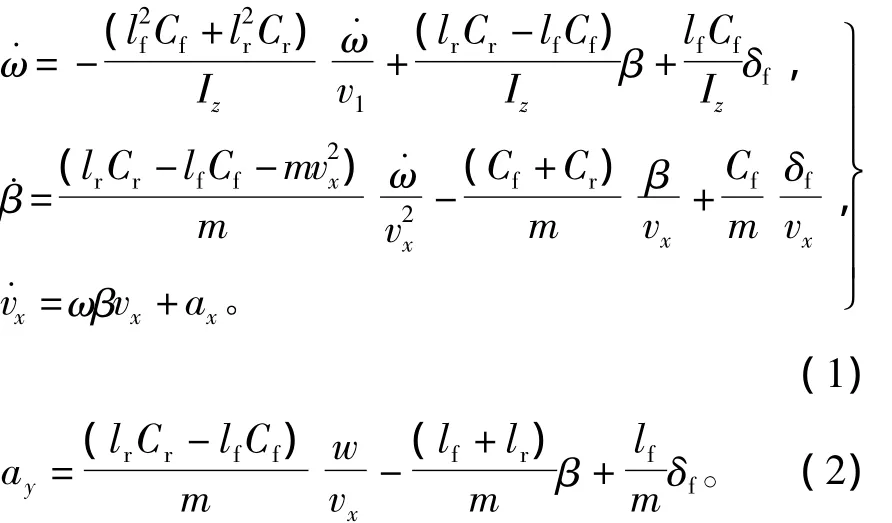
式中:ω为横摆角速度;β为质心侧偏角;vx为纵向车速;δf为前轮转角;ay为侧向加速度;ax为纵向加速度;m为车辆质量;Iz为绕z轴的转动惯量;lf为前轮轴距;lr为后轮轴距;Cf为前轮等效侧偏刚度;Cr为后轮侧偏刚度。

以方向盘转角δsw作为控制输入，设定方向盘到前轮转角的传动比i=16，可得

2 基于软测量技术的汽车状态估计

2.1 软测量技术

软测量技术也称为软仪表技术［10］。基本原理为:利用那些与难于检测的主导变量有密切关系的、容易检测到的辅助变量，通过数学模型运算，得到主导变量的估计值。软测量技术常用的方法包括机理建模分析、回归分析、状态估计、模式识别、神经网络、模糊数学、过程层析成像以及相关分析等。本文采用的基于状态估计的软测量技术，是在建立非线性汽车软测量模型的条件下，根据可测信息集通过运用自适应强跟踪滤波算法推出主导变量的估计值，实现用常规方法难以测量的状态参数的测量。图2为基于软测量技术的汽车状态估计系统。

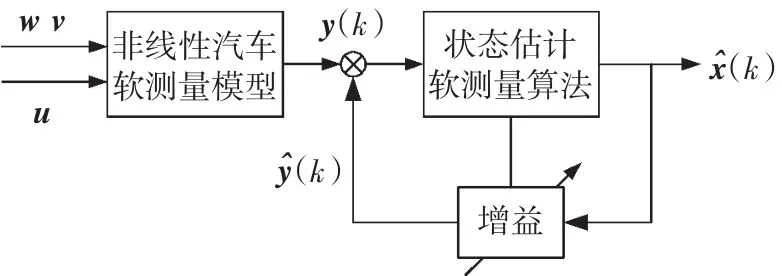
图2 汽车行驶状态估计系统Fig．2 Block diagram of vehicle state estimation system

图2中，w、v和u分别为可测的过程噪声、量测噪声和控制变量。y(k)和(k)分别为对象输出的实际值和估计值，(k)为对象状态的估计值，离散时刻k=0，1，2，…。

2.2 基于自适应强跟踪滤波器的软测量算法

设系统采样周期为T，可将系统离散化为标准的非线性离散系统的状态方程和观测方程， 其形式为

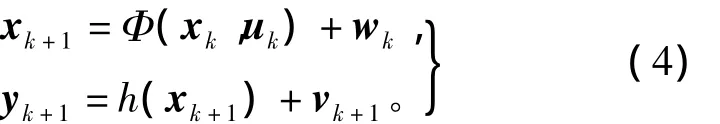
式中:xk为状态向量;yk+1为观测向量;uk为系统输入;wk、vk+1分别为过程噪声和量测噪声，满足为过程噪声协防差阵，)=Rk，Rk为量测噪声协方差阵，E(·)为期望函数;离散时刻k=0，1，2，…，j=1，2，…;Φ、h为非线性或线性向量函数，且具有关于状态的一阶连续偏导数。

传统的扩展卡尔曼滤波器(extended Kalman filter，EKF)局限于需要精确知道系统的数学模型和噪声的统计特性，在大多数情况下，EKF只能给出状态估计的有偏估计，并且对模型误差的鲁棒性较差。汽车作为一个复杂系统，在行驶过程中的噪声特性往往难以统计。为此，针对有未建模误差的动态系统，以及模型参数和噪声统计特性存在未知漂移等问题，本文基于自适应卡尔曼滤波器和STF算法，将系统未建模动态归入虚拟噪声，通过引入多重次优渐消因子在线修正虚拟噪声统计特性来补偿系统的建模误差，得到一种自适应强跟踪滤波软测量算法。该算法的递推过程如式(5)所示，即

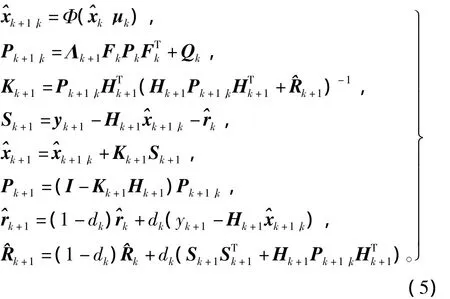
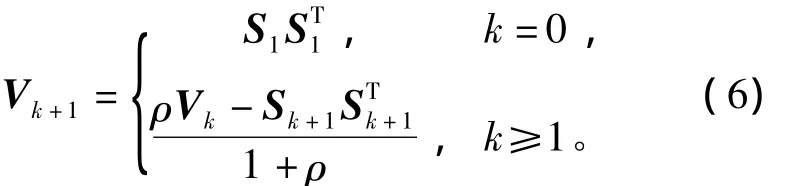
式中，Vk为残差协方差阵。

式中，β为引入的弱化因子。

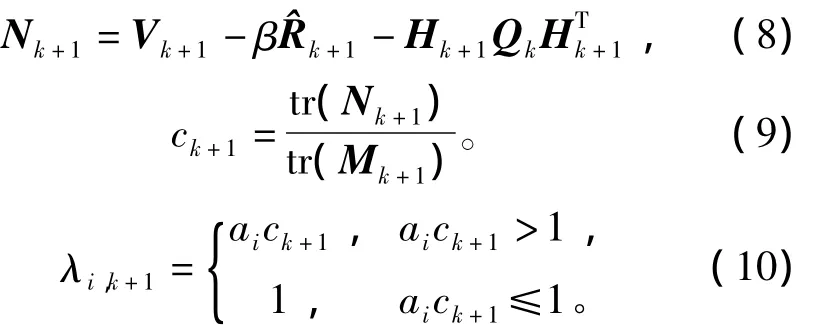
根据STF定义，若引入多重渐消因子矩阵，本文所提出的自适应强跟踪滤波算法必须满足正交性原理，即满足以下两个条件:

2)残差序列保持正交，即

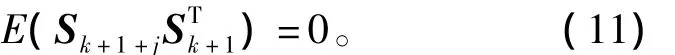
若要证明该算法满足上述正交性原理，先给出如下定理。

定理 1 令 εk=xk-，其中为上述 ASTF算法得到的状态估计值，若计算法复杂度O［|εk|2］≪O［|εk|］成立，则有下式成立，即

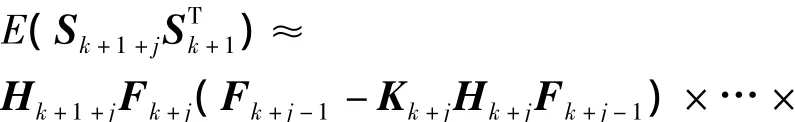
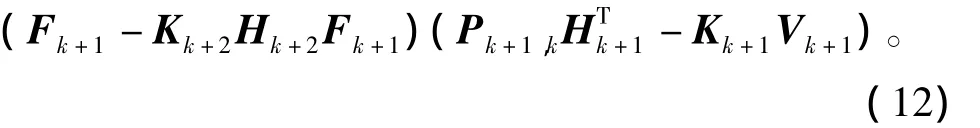
上述定理可按照文献［11］中给出的方法证明，故此处只给出关键证明过程。

证明:由式(5)可得

同理由式(5)可得

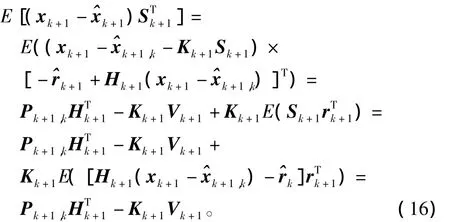
将式(16)代入式(15)，即可得式(12)，于是定理1得证。

根据STF算法，在每一步迭代过程中，应通过在线调整增益矩阵Kk+1，从而满足E(Sk+1+j)=0，k=0，1，2，…，j=1，2，…。根据定理 1，可将此条件转换为选择适当的时变增益矩阵 Kk+1，使得式(17)成立，则正交性原理必然满足。

由此得到式(17)成立的充分条件为

对式(19)两边做求迹运算 tr(·)，并除以tr(Mk+1)，可得式(9)。

至此证明了本文所提出的算法满足正交性原理。

下面给出ASTF算法的迭代步骤:

1)令k=0，设置初始值 x0，P0，噪声协方差阵Q，设置虚拟观测噪声期望和协方差矩阵，设置参数b，ai，ρ，β。

3)由式(14)计算残差协方差阵Vk+1，并连同式(15)～式(18)计算多重渐消因子矩阵Λk+1。

5)由式(7)计算 Pk+1，k，由式(8)、式(10)和式(11)更新增益矩阵Kk+1、状态估计和误差协方差阵Pk+1。

6)k+1→k，若k达到设定结束步数，则终止算法;否则，转向步骤2)继续迭代循环。

3 基于Carsim和Matlab/SIMULINK联合仿真的算法验证与分析

3.1 Carsim和Matlab/SIMULINK联合仿真环境

Carsim［12］是一款由美国 mechanical simulation corporation开发的汽车动力学仿真软件。Carsim软件采用实际车辆的数据可以仿真驾驶员、路面及车辆动力学输入的响应，主要用来预测和仿真汽车的操纵稳定性、制动性、平顺性、动力性和经济性。本文基于Carsim与Matlab/SIMULINK联合仿真环境建立自适应强跟踪滤波器估算汽车状态，通过他为滤波器提供控制输入和测量输出，将算法估计值与输出值进行比较，验证算法的有效性。图3为基于Carsim和Matlab/SIMULINK的仿真框图。

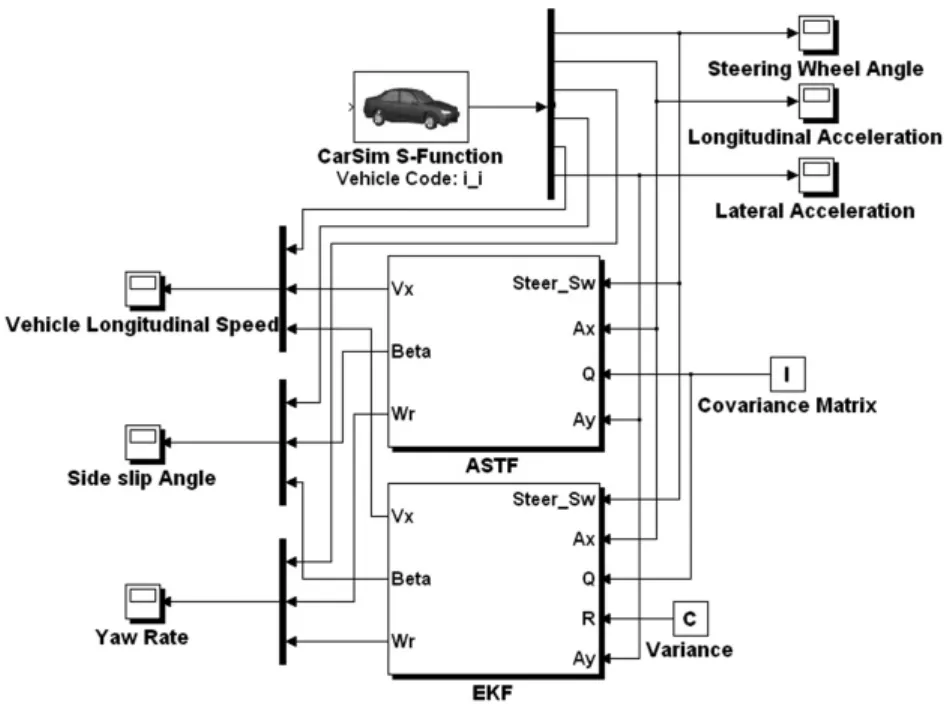
图3 基于Carsim和Matlab/Simulink的仿真框图Fig．3 Block diagram of simulation based on Carsim and Matlab/SIMULINK

3.2 急剧双移线试验

为了验证ASTF算法的准确性、可靠性，采用Carsim中某款SUV的实车参数，并依据ISO3888-1-1999标准，在Carsim中虚拟仿真急剧双移线试验，采样周期为0.025 s。实验中，汽车快速通过路面设定的标杆，路径如图4所示，方向盘回转，根据侧向加速度的观测量估算横摆角速度、质心侧偏角等。

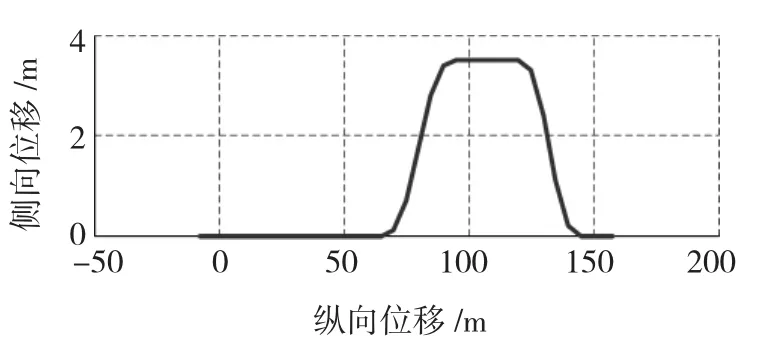
图4 双移线试验行驶路径Fig．4 Path of double lane change test

为了验证ASTF算法对含噪声非线性汽车系统的估计性能，本文对ASTF算法与EKF算法进行比较。图5～图7为基于ASTF算法和EKF算法的车辆纵向速度、横摆角速度、质心侧偏角等关键状态参数的估计结果，并将其与Carsim的实际输出值进行比较。

设置算法的初始参数为:x0=［0 0 0］T;P0=105I3×3;b=0.98;ai=1，i=1，2，3。并设置 ASTF 和EKF具有相同的噪声协方差阵 QASTF=10-5I3×3，QEKF=10-5I3×3。

从图5～图7中可以看出，基于ASTF和EKF算法得到的汽车非线性状态符合实际情况，两种算法的估计值非常接近，误差在可控制的范围内。在t=4～10 s区间内，汽车进入移线行驶状态，纵向车速、横摆加速度及质心侧偏角等状态在此区间内发生急剧变化。由图5、图6(a)和图7(a)可知，由于状态的噪声协方差取值过小，EKF算法在曲线的上升和下降阶段明显存在滞后，而ASTF算法采用了多重次优渐消因子迫使估计残差具有正交性，增强了对突变状态的跟踪能力，从而能够很好地跟踪变化中的状态值。

由图5可知，在汽车纵向速度的估算过程中，当移线行驶结束后，ASTF的估计精确度很高，其估计是无偏的。而EKF算法的估计存在偏差，且通过仿真可知，当取纵向车速的噪声协方差QEKF1为原来的1/10时，EKF算法将获得与ASTF近似的估计精确度。相反，增大QEKF，其估计精确度逐渐下降，甚至发散。在状态变量横摆角速度和质心侧偏角变化曲线的波峰和波谷处，EKF算法的估计偏差要大于ASTF算法的估计偏差，此时各状态变量处于明显的非线性区域，由于ASTF算法中多重次优渐消因子产生调节作用，并自适应修正估计状态的偏差，从而ASTF比EKF具有更高的估计精确度。

由图6(b)和图7(b)可知，当量测值中加入零均值、均方差为0.04的白噪声时，ASTF能有效抑制噪声，且仍具有很高的估计精确度，这是因为算法中所取的噪声协方差较小，能够有效削弱噪声带来的影响，避免引起估计值的波动，同时在多重次优渐消因子的作用下该算法仍能获得很高的估计精确度。而EKF算法随噪声协方差增大，其抑制噪声的能力变弱，导致估计精确度下降。

综上所述，EKF算法的性能受噪声协方差阵、量测噪声的水平等因素的影响很大，而ASTF算法则对此不敏感，能满足系统较大范围内的不确定性;而且当状态变量发生突变时，ASTF算法具有很好的跟踪能力，而EKF算法相对较差。

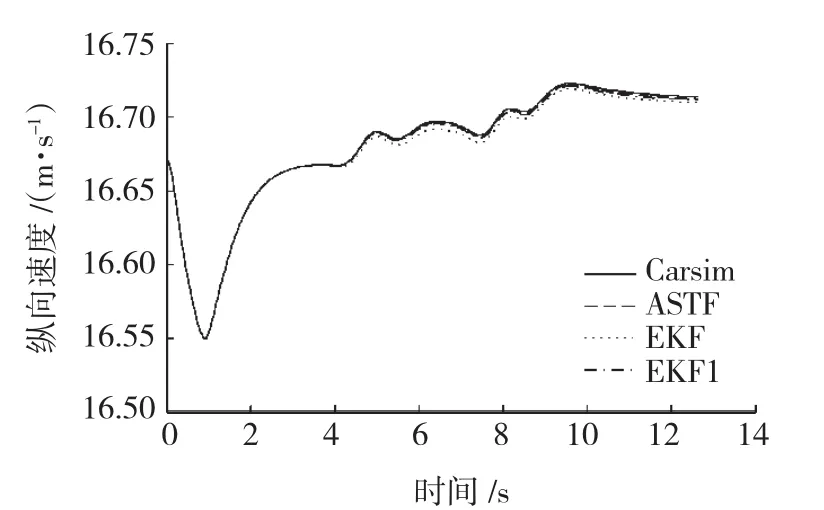
图5 纵向车速的估计值与Carsim输出值的对比曲线Fig．5 Comparison of vehicle longitudinal velocity between estimated value and Carsim value

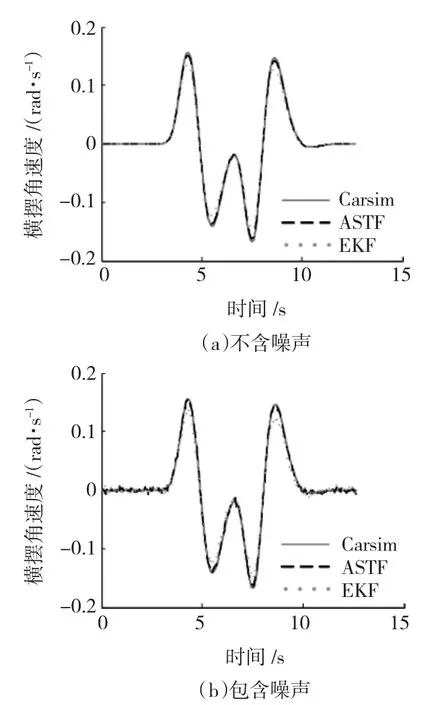
图6 横摆角速度的估计值与Carsim输出值的对比曲线Fig．6 Comparison of yaw rate between estimated value and Carsim value

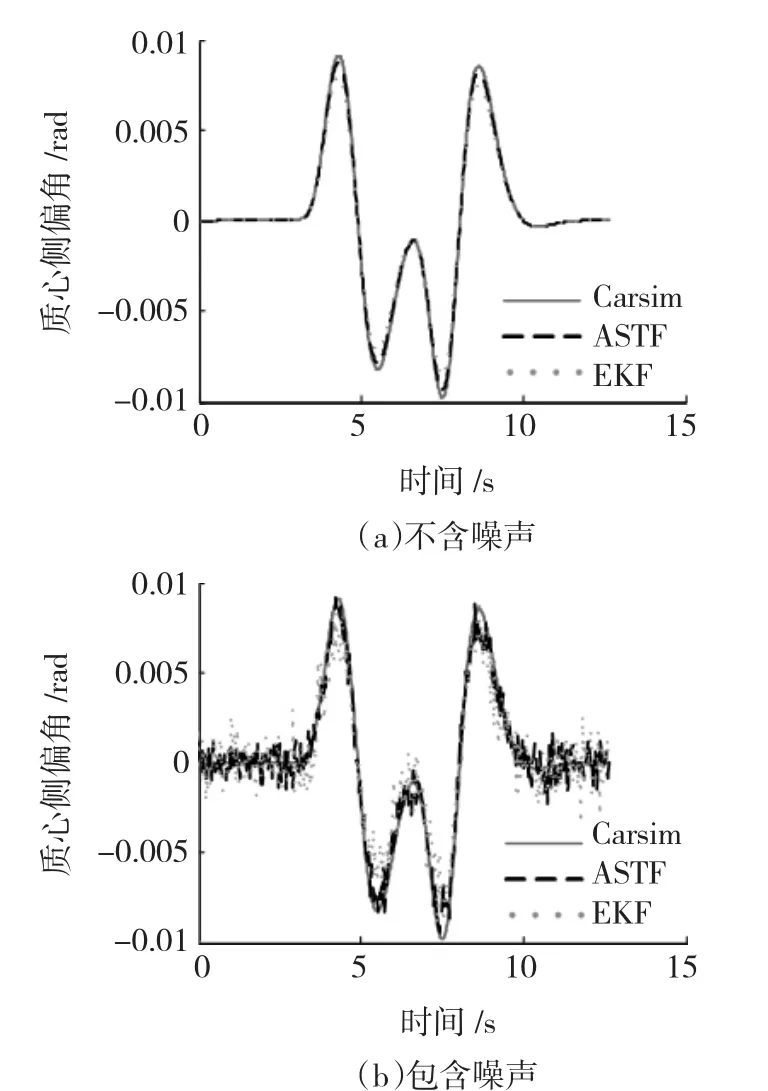
图7 质心侧偏角的估计值与Carsim输出值的对比曲线Fig．7 Comparison of side slip angle between estimated value and Carsim value

4 结语

本文在自适应卡尔曼滤波和STF算法的基础上提出一种适用于状态突变的ASTF算法，并结合简化的3自由度非线性汽车模型，建立了对车身纵向、侧向和横摆稳定性控制所需关键状态的软测量方法。在 Carsim虚拟急剧双移线试验中，采用ASTF算法得到的状态估计值具有很高的精确度，满足汽车状态估计器的对软件性能的要求。通过Carsim和Matlab/SIMULINK联合仿真，比较同等条件下的EKF算法和ASTF算法，仿真结果表明，ASTF算法在估计精确度、跟踪速度和噪声抑制能力等方面均优于EKF算法，能够有效地估计汽车行驶过程中的车速、质心侧偏角和横摆角速度，具有很强的实时性，适用于汽车状态的在线估计。本文在采用实车参数的Carsim仿真环境下，验证了基于ASTF的软测量算法的正确性和有效性。下一步将通过硬件在环仿真技术，将所建立的软测量模型和估计算法应用于实车试验中，进一步验证其实用性和可靠性。

［1］VENHOVENS P J T，NAAB K.Vehicle dynamics estimation using Kalman filters［J］.Vehicle System Dynamics，1999，32(2):171-184.

［2］GUSTAFFSON F，DREVÖ M，FORSSELL U，et al.Virtual sensors of tire pressure and road friction［C］//Proceedings of the 2001 Society of Automotive Engineers(SAE)World Congress，March 5-8，2001，Detroit，USA.2001:010796.

［3］WENZEL T A，BURNHAM K J，BLUNDELL M V.Dual extended Kalman filter for vehicle state and parameter［J］.Vehicle System Dynamics，2006，44(2):153-171.

［4］WENZEL T A，BURNHAM K J，BLUNDELL M V，et al.Kalman filter as a virtual sensor:applied to automotive stability systems［J］.Transactions of the Institute of Measurement and Control，2007，29(2):95-115.

［5］TSENG H E.A sliding mode lateral velocity observer［C］//Proceedings of the 6th International Symposium on Advanced Vehicle Control，September 9-13，2002，Hiroshima，Japan.2002:387-392.

［6］STÉPHANT J，CHARARA A，MEIZEL D.Virtual sensor:application to vehicle sideslip angle and transversal forces［J］.IEEE Transactions on Industrial Electronics，2004，51(2)，278-289.

［7］赵林辉，刘志远，陈虹.一种车辆状态滑模观测器的设计方法［J］.电机与控制学报，2009，13(4):565-570.

ZHAO Linhui，LIU Zhiyuan，CHEN Hong.Design method of sliding model observer for vehicle state［J］.Electric Machines and Control，2009，13(4):565-570.

［8］SAGE A P，HUSA G W.Adaptive filtering with unknown prior statistics［C］//Proceedings of Joint Automatic Control Conference，August 4-6，1969，Washington，USA.1969:760-769.

［9］周东华，席裕庚，张钟俊.一种带多重次优渐消因子的扩展卡尔曼滤波器［J］.自动化学报，1991，17(6):689-695.

ZHOU Donghua，XI Yugeng，ZHANG Zhongjun.A suboptimal multipal fading extended Kalman filter［J］.Acta Autmatica Sinica，1991，17(6):689-695.

［10］李海青，黄志尧.软测量技术原理及其应用［M］.北京:化学工业出版社，2000:30-37.

［11］周东华，叶银忠.现代故障诊断与容错控制［M］.北京:清华大学出版社，2000:60-76.

［12］ANN Arbor.Carsim Reference Manual，Ver6.03［M］.Michigan:Mechanical Simulation Corporation，2005:30-53.