模拟训练机模型简化算法的研究

孟庆松， 原海勃

(哈尔滨理工大学自动化学院，哈尔滨 150080)

0 引言

目前，现代模拟训练机仿真理论及技术已发展成为独立的高科技领域，对于高精确度和昂贵的模拟设备系统而言，其优点尤为明显。由于模拟训练机的仿真品质直接取决于复现被仿真过程参数的精确度，所以仿真过程的数学模型就成为了模拟训练机仿真系统中一个非常重要而又独立的关键部分。而过程数学模型的解算需要求解复杂高阶矩阵方程的数值解，其求解的复杂性使得很多现代模拟训练机控制过程的仿真变得难以全真实时实现。在研究模拟训练机的仿真问题时，在满足人的感官和视觉要求的前提下，通常对其模型的解算进行简化，即对其完成各种实际动作或过程的控制系统采用模型简化的算法加以仿真实现，以适应仿真效果的实时性和真实感。其实，存在许多种系统模型简化的方法，而模型简化的基本方法大致可分为时域法和频域法两种，比较常见的时域法包括连分式法［1］、Pade逼近法［2］、Routh 逼近法［3］等，而频域法包括集结法［4－5］、平衡降阶法［6］等。其中有些方法只适用于单输入单输出系统，有些方法不能保持系统的稳定性，还有些方法无法保证较高的输出精确度。当然也有将模型简化与神经网、预测控制等控制理论相结合的方法，因其实用性、应用范围等因素的限制而实际应用很少。

本文研究的是仿真过程中数学模型的降阶算法和求解高阶矩阵方程的简化仿真算法，提出一种设计思想，即在过程动态时采用通用滤波器的快速仿真算法，在稳态时采用模型降阶和时矩输出拟合相结合的算法。该设计理念不仅适用于多输入多输出系统，还可以保持系统的稳定性、可控性和可观性，并具有较高的输出拟合精确度。采用对过程的模型降阶和动态响应快速仿真等算法，目的是提高过程动态和稳态仿真解算时的准确度和实时性。

1 降阶算法

对于模拟训练机系统数学模型降阶算法，下面简单介绍两种比较典型的方法，即基于内平衡理论的奇异摄动降阶方法和基于有序实Schur分解理论的降阶方法。这两种方法主要针对的是多输入多输出线性稳定系统，具有输出精确度高、灵活简便等优点。

1.1 基于内平衡理论的奇异摄动降阶方法

Moore利用系统的可控、可观的概念，最先提出了一种平衡降阶方法，即所谓系统的内平衡实现理论［7］。基于这种理论，可以确定线性定常、渐近稳定系统的降阶模型。

考虑线性多变量定常系统S1，即

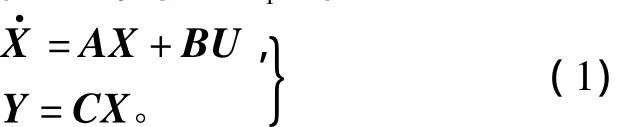
式中:X∈Rn×1为状态向量;U∈Rm×1为输入向量;Y∈Rp×1为输出向量;A、B、C 为常量矩阵。则该系统的传递函数阵为

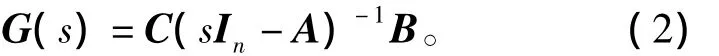
式中，In为n阶单位阵。

1)根据内平衡理论，利用可控与可观Grammian矩阵可将系统S1等价变换为平衡系统S2，即

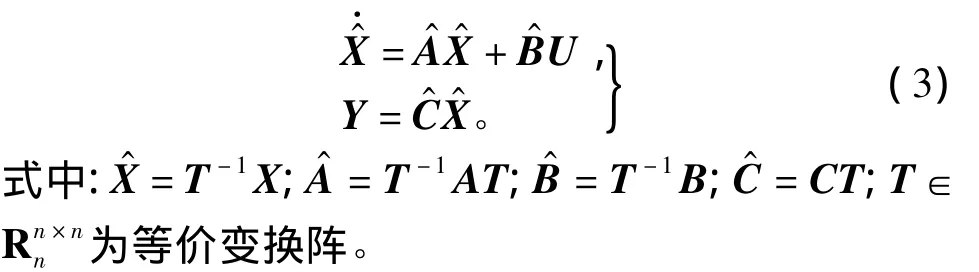
2)根据系统G(s)的奇异值大小分布，可将系统S2作如下形式分解，即

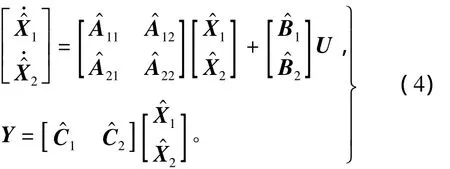
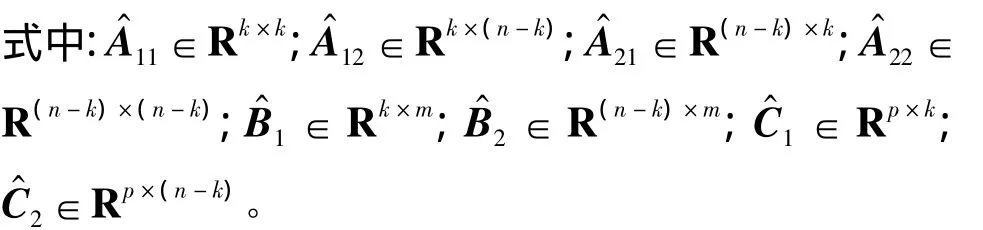
系统G(s)的奇异值σi的定义为σi［G(s)］=［λi(WcWo)］1/2，其中，λi为特征值，i=1，2，…，n，Wc为可控Grammian阵，Wo为可观Grammian阵，而且二者满足Lyapunov方程，即

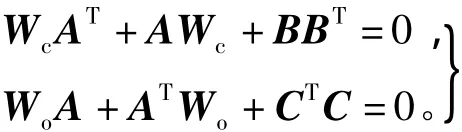
若σk+1≪σk，其中，k为降阶模型的阶次，则状态中的部分基本上不影响系统的输入输出行为，即剔除状态中弱的可控可观部分对系统的行为没太大影响［8］。这说明系统S3:{}是原系统的良好的低阶近似，即低阶模型的传递函数阵为

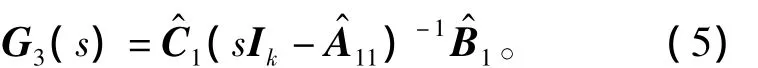
式中，Ik为k阶单位阵。

1.2 基于有序实Schur分解理论的降阶方法

同样对于如式(1)所示的系统，设A阵的特征根按实部递减顺序排列为λ1，λ2，…，λn，且Re［λk］≫Re［λk+1］，其中，k＜n。

1)根据有序实Schur分解定理可知，存在正交矩阵U，使得A阵的有序实Schur分解为

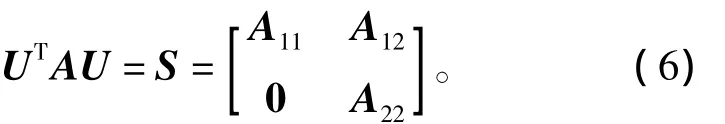
式中:A11∈Rk×k;A12∈Rk×(n－k);A22∈R(n－k)×(n－k);λi(A11)= λi(A)，i=1，2，…，k;UT=U－1;而λ(A11)、λ(A)分别为 A11、A 阵的特征根。

于是，在等价变换T=UV下，原系统S1变为S～

2，即

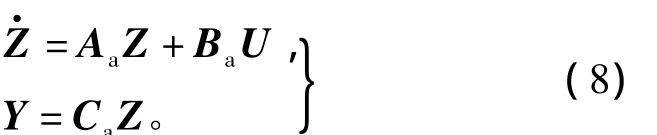
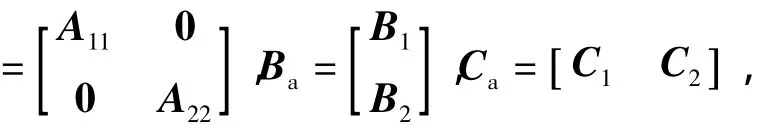
由于U为正交矩阵，且求解Sylvester方程(7)是数值可靠的，所以变换T=UV是数值稳定的。

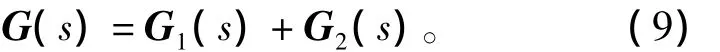
式中:G1(s)=C1(sIk－A11)－1B1;G2(s)=C2(sIn－k－A22)－1B2;而 G(s)=C(sIn－ A)－1B=Ca(sIn－Aa)－1Ba。也就是将原系统S1分成为两个独立的子系统之和，取主导极点子系统作为降阶系统，即

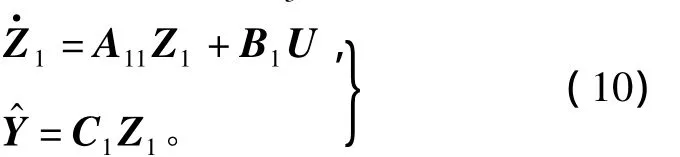
1.3 时矩输出拟合

依据降阶准则，根据式(5)或式(10)可得

下面讨论两种情况:

可以看出，这样得出的降阶模型S4可以保持原系统的稳态值，但由于其前馈传输矩阵为 Dr=，而在一般情况下，矩阵D和原系统的r零阵是不相等的，因此降阶模型S4的初始响应值可能与原系统不一致。

为使降阶模型S4具有与原系统S1相同的初始响应值和相近的稳态值，必须再对所得的系统模型S4加以修正。

首先将模型S4形式修正成模型S5，如式(13)所示，然后再进行其稳态响应值的时矩拟合。

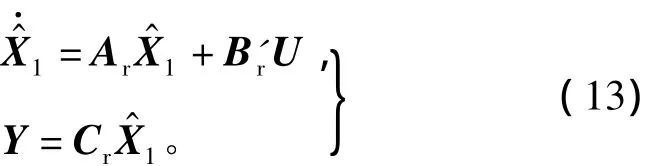
式中，B'r∈Rk×m为需要拟合的输入矩阵。模型形式这样处理可使模型S5与原模型S1具有相同的初始响应值，但为保证二者还具有相同或相近的稳态响应值，则必须满足下列条件，即

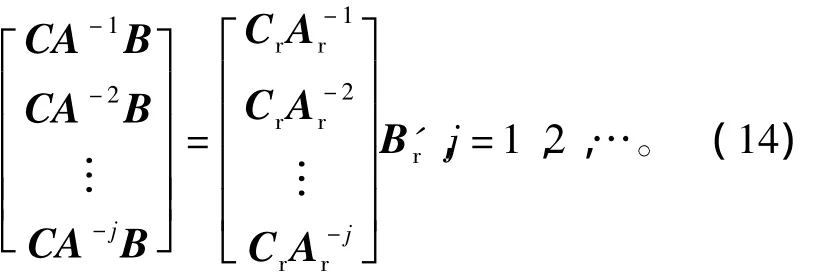
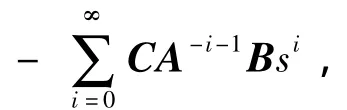
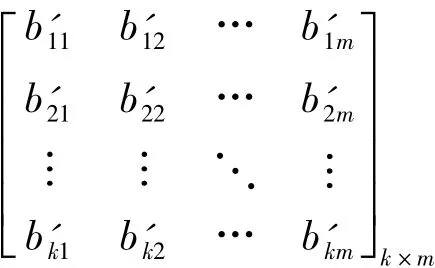
1)当k/p=j，j为整数时，可唯一求得B'r阵。

2)当k/p=j，j不为整数时，利用最小二乘原理化为正规方程组，从而得到其最小二乘解，即以最小误差拟合稳态响应;或者可再适当列写一些方程，使其与矩阵方程(14)构成一个封闭方程组来求解B'r阵。这样使得降阶模型进一步逼近原系统，如在动态响应、稳态响应及相对稳定性等方面作进一步的拟合逼近。

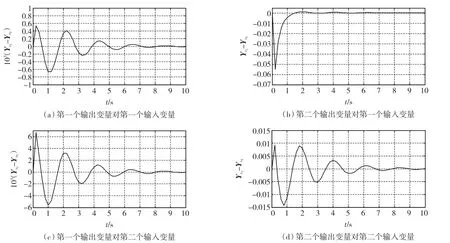
图1 模型S1与S5的单位阶跃响应之差曲线Fig．1 The unit step response difference of Models S1and S5

1.4 实例仿真

对某型号坦克模拟训练机的双输入双输出的六阶控制系统降维到四阶系统，采用上述的基于系统矩阵有序实Schur分解的降阶方法和时矩输出拟合的方法，通过Matlab仿真可以得到六阶原系统与四阶降阶系统的单位阶跃响应之差，其曲线如图1所示。

由图1可知，采用时矩拟合的降阶模型可以满足输出响应的精确度要求，比如在本例的双输入双输出系统的响应中，输出拟合的精确度范围可达输入幅值的0.000 5～0.058倍。还可以通过适当增加降阶系统的阶次进一步提高输出的精确度。

2 通用滤波器的快速仿真算法

为了提高模拟训练机仿真系统的实时性，同时保证人体感受的仿真效果，提出根据通用滤波器的计算结果近似仿真过程动态响应的建模方法。这种方法将系统的动态行为或过程通过通用滤波器的设计方法进行线性拟合，尽可能使通用滤波器的输出较好地逼近系统的实际输出，以满足模拟机的仿真精确度要求。也就是说，针对高阶复杂系统，包括非线性系统，其动态响应的当前值用过去时刻的系统输出值做一个适当的线性组合，达到输出拟合的目的。由于采用线性化拟合的设计思想，使得在线仿真的计算量较小，同时可通过编程灵活地改变其延迟时间和相应的拟合系数以提高仿真精确度。由于需要实时仿真计算的动态模型是大量的，为了降低仿真过程中的计算负荷，不能完全采用如上的降阶方法，而是采用通用滤波器的快速算法对对象过程的动态响应进行仿真拟合。

该算法采用n阶滤波器进行仿真计算时，应遵循以下3个准则:1)使人无法觉察到与原系统的实际动态响应值的偏差;2)过渡过程时间大约为n倍的延迟时间;3)滤波器的参数(包括延迟时间和系数向量)可人为在线修改。

应用n阶滤波器对过程的动态特性快速仿真拟合算法可按如下步骤进行［11］:

1)给定原系统的数学模型及输入信号的形式，并得到相应的输出响应特性;

2)根据原系统的动态特性及变化趋势确定滤波器的延迟时间和滤波器的阶数;

3)将滤波器与原系统的输出响应的初始值点置为重合;

4)按照滤波器系数向量的先后次序分别凑试取值，使滤波器与原系统的输出响应逐步逼近到允许的公差范围之内，一直到二者的响应取得满意的拟合效果，否则再从步骤2)重新修正。

下面给出某模拟训练机一个侧向运动动态模型G(s)，即

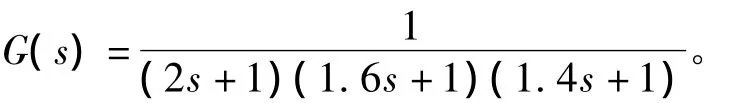
式中:Fk，t=Eke|t－(k+1)τ|，t=0 ～ 511 s;Ek=［0.006，0.005，0.007 4，0.009，0.01，0.01，0.008，0.009］。

通过Matlab仿真，可得到该模型采用通用滤波器的快速算法后的输出拟合曲线，如图2所示。这里需要注意的是拟合过程有一定的延时，所以为了更方便的比对，图2中将原系统与滤波器的方波响应(实际上二者的响应被放大了10倍)平移到相同的时刻上。

这里，输入信号用e表示，拟合延时用τ表示，取τ=20 s。这样，对模型输出y的线性拟合采用下式来进行，即

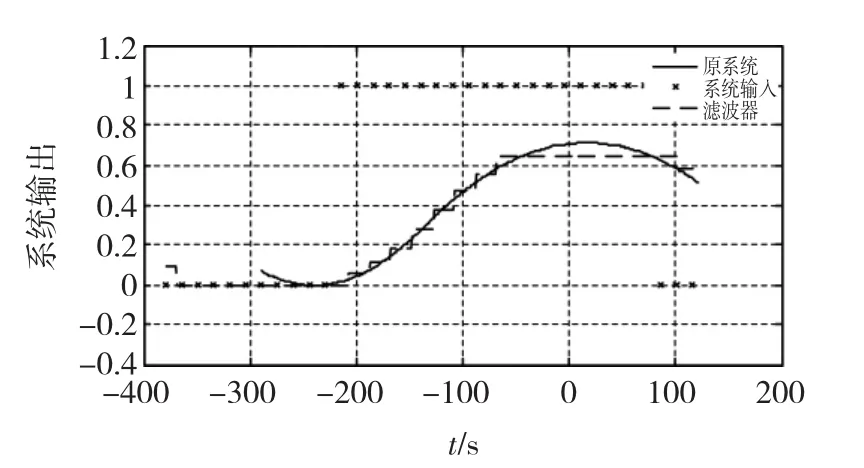
图2 通用滤波器与原系统阶跃响应的输出曲线Fig．2 The unit step response of universal filter and the original system

由图2可知，通用滤波器的输出曲线较好地模拟了系统的实际输出，达到了模拟机仿真的感官效果。

3 结语

通过上述的理论分析可知，基于系统矩阵Schur分解或平衡变换的模型降阶方法适用于多输入多输出的线性系统，可以保证系统的稳定性、可控性和可观性。从仿真的结果来看，在动态时为了提高实时性，简化模型的解算过程，可以采用通用滤波器的快速仿真算法，以达到人体感官满意的模拟效果，而在稳态时为了提高简化模型的近似精确度，可以采用模型降阶和时矩拟合相结合的算法，以获取更高的输出拟合精确度。因此，在模拟训练机控制系统的仿真和建模时，将对象仿真的过程分为动态和稳态两个阶段，过程的动态特性仿真通过通用滤波器的设计方法进行简单的线性拟合，尽可能使通用滤波器的输出较好地逼近系统的实际输出，以达到模拟机对人体感官的仿真效果。而稳态特性则采用基于系统矩阵Schur分解或平衡变换的模型降阶与时矩输出拟合相结合的算法以获取较高的拟合精确度。这样，在实际系统工作时可大大缩短计算模型所耗费的机时，提高过程模拟的反应速度。

［1］张启人．线性系统频域模型简化的连分式法［J］．信息与控制，1981，5(3):1－11．

ZHANG Qiren．Continued fractions methods of frequency domain model reduction of linear systems［J］．Information and control，1981，5(3):1－11．

［2］胡锡恒．保留主模式的FF-Pade法降阶［J］．信息与控制，1984，13(6):32－35．

HU Xiheng．Retain the main mode of FF-Pade method reduced order［J］．Information and control，1984，13(6):32 －35．

［3］万百五，吴受章．大系统的模型简化［J］．自动化学报，1980，6(1):57－66．

WAN Baiwu，WU Shouzhang．Model reduction of large scale system［J］．Acta Automatica Sinica，1980，6(1):57 －66．

［4］曹长修，王万良．集结降阶方法及其在系统设计中的应用［J］．重庆大学学报，1990，13(3):12 －19．

CAO Changxiu，WANG Wanliang．Aggregation method and its application in system design［J］．Journal of Chongjing university，1990，13(3):12－19．

［5］王炎生，陈宗基．基于系统矩阵实Schur分解的集结法模型降阶［J］．自动化学报，1996，22(5):597－600．

WANG Yansheng，CHEN Zongji．Aggregation model reduction based on real Schur decomposition of system matrix［J］．Acta Automatica Sinica，1996，22(5):597 －600．

［6］胡明华，胡寿松．平衡降阶方法及其发展［J］．南京航空学院学报，1990，22(4):92 －100．

HU Minghua，HU Shousong．Balance reduced-order method and its development［J］．Journal of Nanjing Aeronautical Institute，1990，22(4):92－100．

［7］MOORE B C．Principal component analysis in linear system:controllability，observability and model reduction［J］．IEEE Transactions on Automatic Control，1981，26(1):17 －32．

［8］МЭН Цинсун，ШЕСТАКОВ К М．Метод упрощения моделей для сложных систем управления［J］．Вестн Белорус Гос Унта Cер 1，2008，20(3):44 －51．．

［9］RACHID A，HASHIN G．Model reduction via Schur decomposition［J］．IEEE Transactions on Automatic Control，1992，37(5):666－668．

［10］МЭН Цинсун，ШЕСТАКОВ К М．Упрощение математических моделей объектов в тренажерных комплексах［J］．Инженерно-физический Журнал，2009，82(3):590 －599．

［11］МЭН Цинсун．Универсальный фильтр имитации динамических объектов в тренажерных комплексах［J］．Электроникаинфо，2009，10(8):74－76．