谐波电流检测方法公式推导及内在联系探究

丁宁 张加胜

（中国石油大学（华东）信息与控制工程学院，山东 东营 257061）

0 引言

随着电力电子装置的广泛应用，大量非线性负荷的投入运行，致使电网的谐波污染越来越严重，谐波和无功功率的补偿问题也日益受到重视。在要求对变化的谐波和无功功率进行快速动态补偿的场合，建立在平均值基础上的传统功率理论已难以使用。80年代初，日本学者赤木泰文（H.Akagi）等人提出了建立在瞬时值基础上的三相电路瞬时无功功率理论［1，2］，而基于此理论的谐波和无功电流实时检测方法成功应用于有源电力滤波器，有力推动了有源电力滤波器的研究和发展，同时以瞬时无功功率理论为基础的谐波和无功电流检测方法也得到了广泛的应用。

目前使用的基于瞬时无功功率理论的谐波和无功电流检测方法主要有p－q法、d－q法、ip－iq法［3］。有些文献中臆断地认为d－q法中的idqd、idqq与ip－iq法中的ip、iq对应相等，其实并非如此。本文从数学角度详细推导了三种方法所用变换式的表达式，以变换式为切入点揭示三种检测方法的内在联系与区别。

1 三种检测法所用变换式的推导

1.1 p－q法

为简明起见，本文均只考虑电压和电流中不含零序分量的情况。设三相电路的瞬时电压和瞬时电流分别为ua、ub、uc和ia、ib、ic，将它们变换到两相正交的α－β坐标系上，可得两相瞬时电压uα、uβ和两相瞬时电流iα、iβ如下［4－5］:

如图1所示，空间直角坐标系α－β－γ为右手坐标系，在αβ平面内uα、uβ和iα、iβ分别合成为电压矢量→■u和电流矢量→■i。瞬时无功功率理论定义三相电路的瞬时有功功率p和瞬时无功功率q分别为电流矢量与电压矢量的点积和叉积，即:

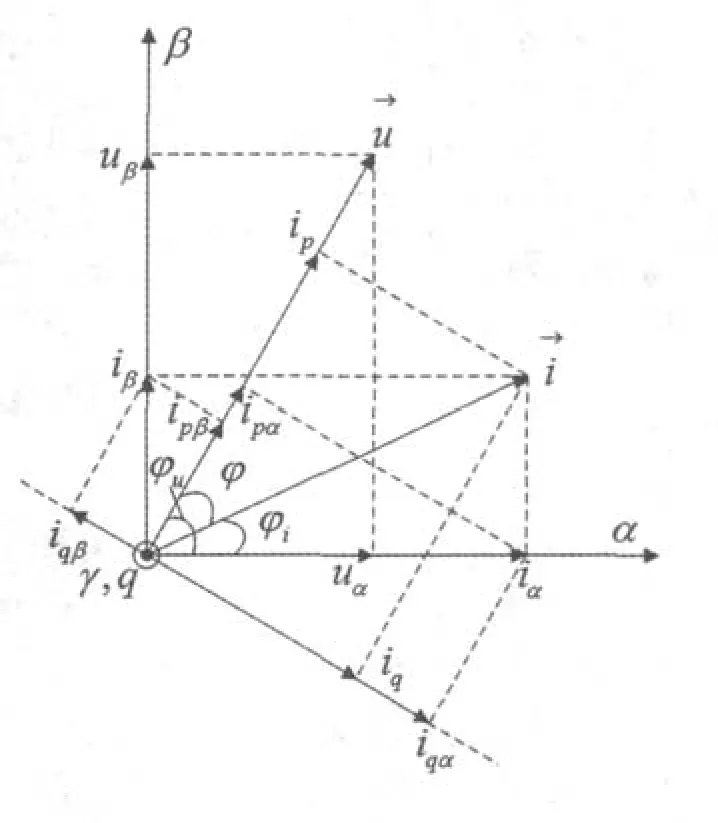
图1 瞬时无功功率理论定义的电压、电流矢量图

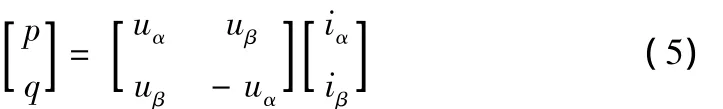
式（1）、（2）、（5）即为p－q法所运用的变换式。

1.2 d－q法

d－q变换（park变换）是在解决同步电机模型中时变系数这一问题而被广泛应用的一种数学变换。如图2，abc为同步电机定子绕组，dq为转子绕组，由于转子的旋转和凸极效应，在abc坐标下的同步电机方程中存在大量变化参数，给分析和计算带来了很大困难，为解决这一问题，电机学中通常把abc三相绕组经过适当变换得到与定子绕组等效的并与转子同步旋转的dq绕组，这就是派克变换［6］。

下面简要推导dq变换，以便于比较d－q法与ip－iq法的异同，更好地理解两种方法的本质。如图2所示，由三相abc到两相αβ 坐标变换过程中运用直接投影法，iα、iβ可以分别看成ia、ib、ic向α、β轴上投影得到的投影之和，同时为消除正反变换矩阵之间的系数差异，采用恒功率变换，变换矩阵前添加系数，可得:

图2 派克变换对应的矢量图

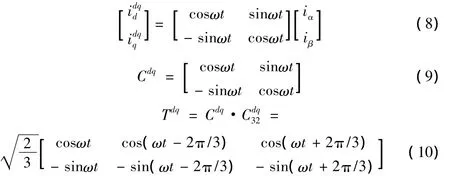
这就是被广泛使用的恒功率下的park变换式，即为d－q法所用变换式。

1.3 ip－iq法

设三相电压表达式为:

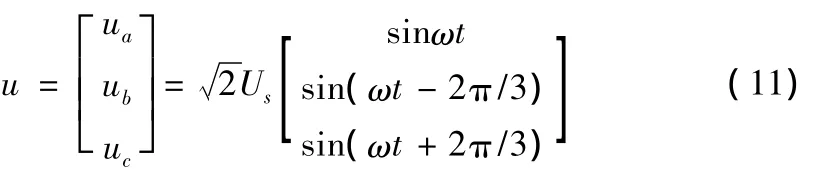
其中Us为相电压有效值

取a轴为复平面的实轴，滞后实轴90°电角度为虚轴，如图3所示，则b轴和c轴的位置分别为ej23π和e－j23π，则电压空间矢量为:

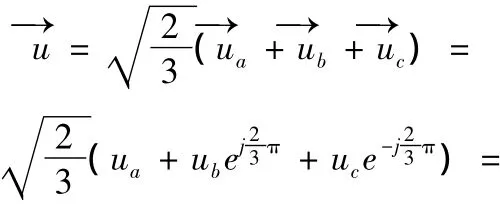
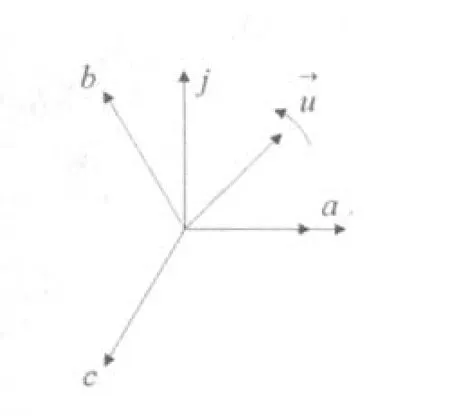
图3 电压矢量合成示意图

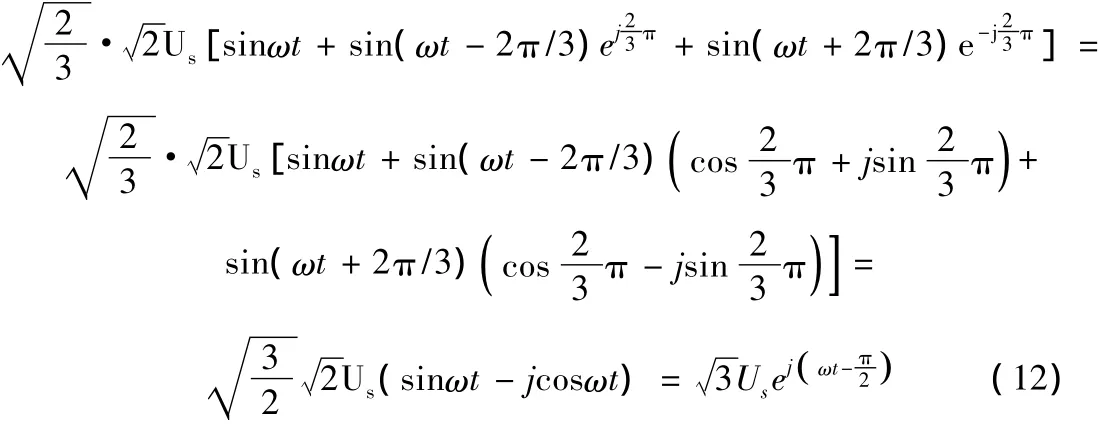
由此可知电压空间矢量为一个恒幅等速旋转的矢量，幅值和幅角大小分别为:

瞬时无功功率理论定义瞬时有功电流ip和瞬时无功电流iq分别为电流矢量在电压矢量及其法线上的投影［7，8］，又因电流矢量 在αβ坐标系下可分解为iα和iβ两个分量，因此瞬时有功电流ip可表示成iα和两个分量在电压矢量 上的投影的叠加，同样地瞬时无功电流iq也可表示成iα和iβ两个分量在电压矢量→法线上的投影的叠加，如图1所示，可得式:

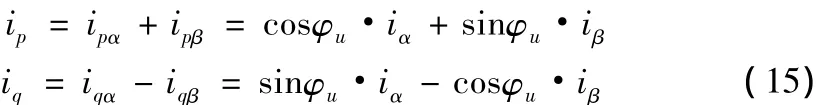
将式（15）写成矩阵形式

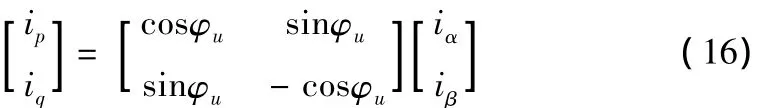
将式（14）代入式（16），可得式（17）

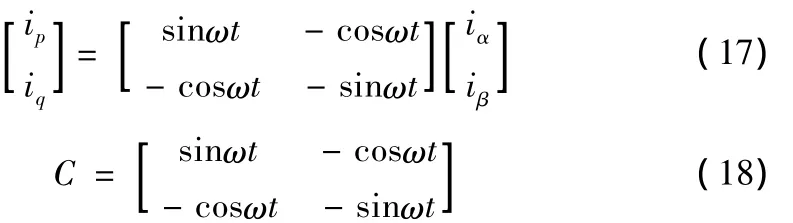
将（2）式代入（17）式得ip－iq法的所用变换的表达式:

2 内在联系

一在相同的基准（α轴），则需将ip－iq坐标系顺时针旋转90°得到i'p－i'q坐标系，这样，ip、iq与、之间的关系便十分明了，可用下式描述:

图4 d－q与ip－iq坐标系关系图

该结论可由式（10）与（19）得到验证。

3 结束语

本文通过严格的数学推导详细分析了导致三种检测方法异同的原因所在，揭示了三种检测方法所用变换式的内在联系，如式（20）和（21）所示。本文的分析及结论使p－q法、ip－iq法变换原理更加清晰、明了，d－q法则不再是纯粹的数学变换，而有了一定的物理意义，其中式（21）揭示了d－q坐标系下idqd、idqq与瞬时无功功率理论中的ip、iq的对应关系，可以得出d－q坐标系下两个量的物理意义:idqd、idqq分别是瞬时无功功率理论中瞬时无功电流、瞬时有功电流的负值。这些分析与结论对理解和改进谐波电流检测方法和有指导意义。

［1］王兆安，杨君，刘进军，等.谐波抑制和无功功率补偿［M］.北京:机械工业出版社，2005.

［2］殷波，陈允平，等.α－β坐标系下瞬时无功功率理论与传统功率理论的统一数学描述及物理意义［J］.电工技术学报，2003，18（5）:42－45.

［3］陈诚.基于瞬时无功功率理论的谐波电流检测法原理及内在联系探究［J］.兵工自动化，2008，27（8）:56 －58.

［4］刘进军，王兆安.瞬时无功功率与传统功率理论的统一数学描述及物理意义［J］.电工技术学报，1998，13（6）:6 －12.

［5］唐蕾，陈维荣.瞬时无功功率理论坐标变换的推导及谐波电流检测原理分析［J］.电网技术，2008，32（5）:66 －69.

［6］倪以信，陈寿孙，张宝霖.动态电力系统的理论和分析［M］.北京:清华大学出版社，2002.

［7］ AkagiH，Kanazawa Y，Nabae A.InstantaneousReactive Power Compensators Comprising Switching Devices without Energy Storage Components［J］.IEEE Trans Ind Appl，1984，20（3）:625 － 630.

［8］王兆安，李民，卓放.三相电路瞬时无功功率理论的研究［J］.电工技术学报，1992，7（3）:55－59.