某扫雷犁系统GA-BP神经网络建模

钱进 陈机林

(南京理工大学机械工程学院，江苏 南京210094)

0 引言

某武器扫雷犁系统，采用犁刀将地雷翻出并推至两侧，达到清扫地雷，提高己方战场机动能力的目的。由于传统的建模方法难以精确描述非线性特性，所以本文选用神经网络对系统进行建模。

采用误差往回传播(Back-Propagation，BP)学习算法的前馈型神经网络简称BP［1，2］网络。BP神经网络是神经网络中应用最广泛的算法，但存在一些缺陷:一是学习收敛速度太慢;二是不能保证收敛到全局最小点;三是网络结构不易确定。遗传算法(Genetic Algorithm，GA)是模拟生物在自然环境中的遗传和进化过程而形成的一种自适应全局优化概率搜索算法，它具有很强的宏观搜索能力和良好的全局优化性能。将遗传算法与BP网络相结合，训练时先用遗传算法对神经网络的权值进行寻找，将搜索范围缩小后，再利用BP网络来进行精确求解，可以达到全局寻找和快速高效的目的，并且可以避免局部极小问题。

作者在对扫雷犁电液伺服系统建模时，将遗传算法应用于BP网络中，增强了在搜索过程中自动获取和自应用控制搜索过程的能力［3］，极大地改善了建模结果，并将其应用到实际系统中，实验结果充分证明了该方法的有效性。

1 扫雷犁系统工作原理

本文研究的某扫雷犁电液伺服系统，主要由电液伺服阀、液压缸、犁刀、仿形靴、轴角传感器等元件组成，其原理图如图1所示。

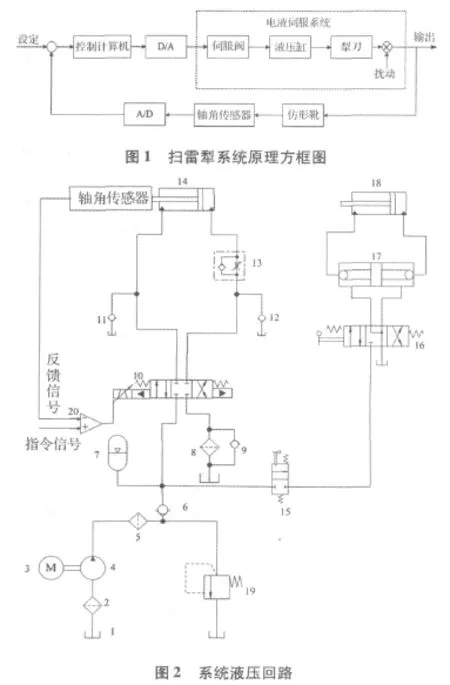
系统的工作流程是:控制计算机根据扫系统设定的入土深度计算出相应的控制信号，D/A转换后传送至伺服放大器中;在伺服放大器中对输入信号进行调理，再送至电液伺服系统中，控制液压缸把动力作用到扫雷犁上，最后控制扫雷犁在设定深度进行扫雷。犁刀的实际位置信号又经过仿形靴和轴角传感器反馈回控制计算机中，构成完整的闭环控制系统，实现对扫雷犁深度的自动控制。

根据系统液压回路和具体参数要求建立AMESim模型，系统模型如图2所示。

元件的主要参数设定:

(1)齿轮泵:额定压力:16MPa最高压力:20MPa额定转速:1800r/min

容积效率:≥0.9 机械效率:≥0.9

(2)犁刀升降伺服阀:额定流量:20L/min A、B、P口工作压力:≤31.5MPa

(3)溢流阀:通径:6mm 工作压力:31.5MPa 最大流量:30L/min

(4)液压缸:液压缸行程:400mm 缸径:φ100mm 杆径:φ55mm

最低启动压力:0.4MPa 额定压力:25MPa

(5)负载:重量:40kg 摩擦力:500N 粘性摩擦系数:0.05N(m/s)

阻尼系数:4N(m/s)

2 GA-BP网络的设计与辨识

针对BP算法局部极值的缺点，考虑使用遗传算法和BP算法结合的GA-BP算法。GA的特点是并行搜索，演算简单，搜索效率高，不存在局部收敛;GA有很强的宏观搜索能力，且找到全局最优解的概率大，所以用它来完成前期搜索能较好的克服BP算法的缺点。相关研究表明，GA-BP［4］混合算法训练的效率和效果比单独使用其中任意一种训练方法要有明显改善。

采用GA-BP算法训练网络过程有2个步骤:先用GA优化网络的初始权(阈)值，在某范围内找到全局最优解;再利用BP算法修改网络权(阈)值，从而得到精确解。

2.1 遗传算法GA优化权值

遗传算法是基于种群遗传学和自然选择的全局搜索与优化算法。基本流程如图3所示。

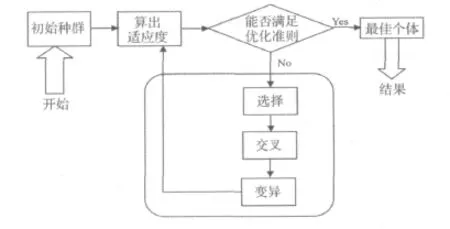
图3 遗传算法基本流程

遗传算法中，—般依据问题的不同可选择不同的优化准则。例如，可采用以下准则之一作为判断条件:种群中个体的最大适应度超过预先设定值;种群中个体的平均适应度超过预先设定值;世代数超过预先设定值。

设网络输入层有R个节点，输出层有N个节点，第一隐含层i个节点，第二隐含层j个节点，则染色体长度的计算公式为L=i×R+j×i+N×j+i+j+N+1，最后一位用于记录每次计算适应度函数的值，其初始值设为0。在预设的范围内随机生成L个数，等同于一个染色体，即:Wk={a1，k，a2，k，a3，k，…，aL-1，k，0}，k=1，2，…，P染色体共有P个，种群规模也为P。每个染色体输入层到第一隐含层的权值为a1～ai×R，第一隐含层到第二隐含层的权值为 ai×R+1～ ai×R+j×i，第二隐含层到输出层的权值为ai×R+j×i+1～ ai×R+j×i+N×j，输 入 层 到 第 一 隐 含 层 的 阈 值 为ai×R+j×i+N×j+1～ ai×R+j×i+N×j+i，第一隐含层到第二隐含层的阈值为 ai×R+j×i+N×j+i+1～ ai×R+j×i+N×j+i+j，第二隐含层到输出层的阈值为 ai×R+j×i+N×j+i+j+1～ aL-1。由于浮点数编码精度高，搜索空间大，所以权重染色体采用浮点编码。后边用到的遗传算子也都是基于浮点编码运算的。

在遗传算法的进化过程中，是由适应度函数来完成对染色体评价的，选择运算的依据是适应度函数的值。一方面，个体适应度值不会有负值;另一方面，较优个体与较劣个体间适应度值必须存在一定差异。所以，目标函数选用均方根误差:式中:ti为期望输出，Q为训练样本数，yi为网络输出。适应度函数为fit=e-E由E≥0求得个体适应度e-E∈(0，1］［16］。

GA-BP算法的设计及参数选取:

用设计好的BP网络试算，根据得出的网络权(阈)值初步设计初始种群范围并随机产生N组。

在选定的GA算法参数中，种群规模为80，遗传代数为1000，编码方式为浮点编码，交叉概率为0.6，变异概率为0.05。

利用交叉、变异、选择等操作算子完成对权(阈)值的不断优化，直到达到遗传操作目标为止。

将优化好的权(阈)值作为网络的初始权(阈)值，并通过BP网络进行精确训练。

2.2 BP网络辨识过程

(1)输入输出的选择

四个输入变量为 xi=［u(k-1)，u(k-2)，y(k-1)，y(k-2)］，输出变量为Y=y(t)。u为阀的电流控制信号，y为扫雷犁刀的吃土深度信号。

(2)样本数据

由于承担该课程教师在企业食品质量安全管理方面经验不足，因此教学多依赖于教材，而教材内容未能与近些年国家快速更新食品质量安全管理类法律法规、标准及时跟进，导致教师教学内容陈旧和过时现象时有发生。

独立采集两组数据，1000组用于训练网络，另1000组用于检验网络的泛化能力。

(3)期望误差

衡量模型精度和泛化能力采用均方根误差(Root Mean Square Error，RMSE):

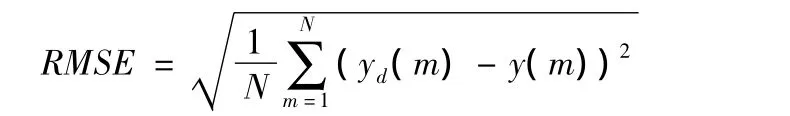
式中yd(m)是模型的期望输出，y(m)是模型的实际输出，N是样本数目。均方根误差越小，表示模型越接近实际系统。

输入节点 xi，隐节点 zj，输出节点 y，其中 i=1，…，4，j=1，2，…，6。ωij是输入节点与隐节点间的网络权值，vj是隐节点与输出节点间的网络权值，θj是隐层的阈值，ym是输出节点的期望输出，y是网络的计算输出。

采用离线辨识的方法，输入节点与隐节点间的网络权值ωij、隐节点与输出节点间的网络权值vj，隐层的阈值θj的初始化结果如下。

3 实验

通过AMESim与Simulink的接口模块可以将Simulink中的激励信号传输到AMESim模型中的伺服阀，同时也可以将AMES-im中扫雷犁系统的吃土深度信号反馈到Simulink模型，从而实现联合仿真。搭建的Simulink模型如图4所示。

图4 数据采集模型

输入信号为伪随机多元信号，采样周期为10ms，仿真时间设为10s，运行一次可采集到1000组数据。多次运行后，取出系统在工作范围内的2000组数据，前1000组用于建模，后1000组用于模型检验。得到的输入输出数据如图5、图6所示，两图中图(a)为伺服阀的控制信号，图(b)为扫雷犁刀的深度信号。

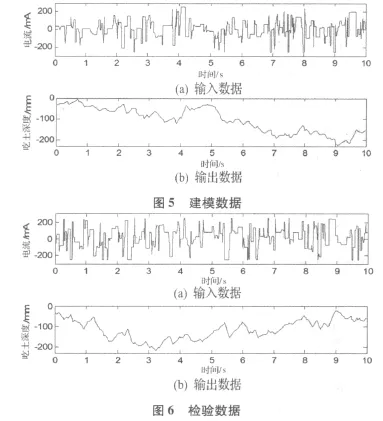
图7和图8是经过归一化处理的，因此纵坐标无单位，只代表一个相对数据。图7为网络训练曲线，横坐标为迭代次数，纵坐标为每次训练误差的加权平方和。从曲线趋势可以看出，网络误差下降速度快，从而充分说明该算法的快速性。图8a为实际样本与对应网络输出间对比，b为网络输出与实际样本间的相对误差，相对误差范围为±0.05，达到实现对扫雷犁电液伺服系统精确建模的目的。

4 结束语

针对某扫雷犁电液伺服系统这一典型非线性系统的建模问题，提出用AMESim和Simulink联合仿真建立非线性电液伺服系统模型，然后通过GA-BP神经网络进行辨识。实验结果与其他建模方法相比，不存在局部收敛，学习速度较快，辨识的效果较好。下一步的工作就是处理实际应用中的问题并实现对该电液伺服系统的控制，从而达到扫雷的效果。

［1］周开利，康耀红.神经网络模型及其MATLAB仿真程序设计［M］.北京:清华大学出版社，2005:69-83.

［2］阮晓刚.神经计算科学［M］.北京:国防工业出版社，2006:354-367.

［3］Slotine，J.J.E.and Li，W(1991).Applied Nonlinear Control［M］.Prentice-Hall，Englewood cliffs，N.J，1991.

［4］张德丰.MATLAB神经网络应用设计［M］.机械工业出版社，2009:262-266.