矿井涌水水源判别的GRA-SDA耦合模型

徐 斌 ，张 艳 ，姜 凌

（1. 长安大学 环境科学与工程学院，西安 710054；2. 长安大学 国土资源部干旱、半干旱地区水资源与国土资源环境开放研究实验室，西安 710054；3. 长安大学 地球科学与资源学院，西安 710054）

1 引 言

在各种矿井灾害中，水害是一种发生频繁、破坏性很强的灾害，水害的发生直接影响到生产的顺利进行和生命财产安全，如何防治水害是管理者和科研人员必须解决的难题。水害主要表现形式为矿井涌水（突水），涌水水源的差异决定了不同的防治措施，因此，对涌水水源的正确判别是防治水害的关键环节。

在科学研究和生产实践的过程中，已经产生了多种多样的水源判别方法并付诸于实际应用。这些方法可以划分为物理分析法（水温、水位）、化学分析法（水化学类型、同位素、放射性元素）、数理统计分析法（灰色系统、模糊数学、多元统计、支持向量机）和复合方法（地理信息系统、可拓识别方法）[1－9]。实际应用中，针对水文地球化学数据的数理统计方法在经济和技术上具有较高的可行性，但目前的判别方法多为单独使用，水源判别的结果往往因方法不同而各异，水源判别准确性无法得到保证。

本文选取灰色关联分析和逐步判别分析作为基础模型，分析了现存问题并提出耦合判别思路，进而设计并建立一种耦合式水源判别模型。为了验证耦合模型的有效性和实用性，本文使用矿区实际样本数据进行了建模与应用，并与传统模型进行了对比分析。

2 GRA-SDA耦合判别模型原理

矿井造成威胁的水源主要来自厚层灰岩岩溶水、其他强富水含水层或地表水。不同水源存在环境和水交替强弱的信息在水化学特征上的表现不同，因此，水化学特征的分析研究，是判别矿井涌水来源的有效方法[10]。目前，针对水化学特征进行分析的方法主要是数理统计方法，经过筛选后选择了灰色关联分析（grey relational analysis, GRA）和逐步判别分析（stepwise discriminant analysis, SDA）为基础判别模型，从而构造了矿井涌水水源判别的GRA-SDA耦合模型。

2.1 基础判别模型简介

2.1.1 灰色关联分析

灰色关联分析是一种多因素统计分析方法，它是以各因素的样本数据为依据，用灰色关联度来描述因素间关系的强弱、大小和次序的。如果样本数据列反映出两因素变化的态势（方向、大小、速度等）基本一致，则它们之间的关联度较大；反之，关联度较小[11]。与传统的多因素分析方法（相关、回归等）相比，灰色关联分析对数据在样本数量和分布规律上要求较低，计算量小，且能有效避免反常情况发生[12]。灰色关联分析被广泛应用于社会、经济、农业、工程等各行业领域的系统分析中。

2.1.2 逐步判别分析

凡具有筛选变量能力的判别分析方法统称为逐步判别分析法[13]。逐步判别分析基本思想是逐步引入变量，并按照变量重要性的变化进行筛选，然后分组进行判别，并在筛选和判别步骤中，进行相应的统计检验。

由于逐步判别分析仅引入判别能力较强的变量参与建立判别函数，当变量数量较大时，与普通判别方法相比较，逐步判别分析具有整体计算量小、判别准确率较高的优点。其缺点是当进行多组逐步判别时，变量筛选受到不同类型的训练样本组合影响，结果具有不确定性。另外，变量筛选过程繁琐，当变量数量并不大时增加了额外的计算量。

2.1.3 基础模型在水源判别中存在的问题

灰色关联分析应用于水源判别中，根据待判别水样与参考水样的关联度可以筛选出关联性最大的水源类型，从而确定待判别水样的水源类型。但有时当待判别水样与个别参考水样呈现较大关联度时，却与各个类型水源的整体关联趋势相悖，这种情况下往往会导致误判。这是由于灰色关联分析是基于系统定性分析的基础之上而建立的定量分析，参考水样个体的类型划分正确与否对于最终的判别结果具有决定性影响，当参考水样个体的类型划分出现偏差时，必然导致误判。

逐步判别分析是基于训练样本的统计分析来进行变量筛选的，在进行多组判别时，某一组类型训练样本是否参与分析会导致不同的筛选结果。在多种类型组合的逐步判别中，需要对所建立的判别函数分别进行判别效果检验，才能确定出合适的判别分析模型用于涌水水源判别。在待判别水样的相关水源类型范围可以确定时，可以较好地进行判别并根据后验概率进行最终评价。在待判别水样的相关水源类型范围无法确定的情况下，需要对多个水源类型进行组合来进行逐步判别，这种情况下往往会出现多个后验概率较高但类型截然不同的判别结果，无法直接确定待判别水样的水源类型。

2.2 GRA-SDA耦合判别模型

2.2.1 耦合模型判别思路

针对上述灰色关联分析和逐步判别分析自身的特点以及在水源判别中所出现的问题，将两种模型进行耦合，其基本思路是：首先，对待判别水样与参考水样进行灰色关联分析，对分析结果进行汇总排序，提供与待判别水样相关联的各个水源类型的排序；然后，根据待判别水样对应的水源类型的关联度排序，对参与判别的水源类型进行筛选；最后，将水源类型数据、参考水样数据和待判别水样数据输入，进行逐步判别分析，获得最终的判别结果。其实质就是通过灰色关联分析来明确参与逐步判别的分组类型范围，消除弱相关类型的样本数据对变量筛选的影响，提高分析效率和分析结果的准确性。

2.2.2 耦合模型的构建

为了建立耦合模型，对问题进行如下定义：假设有未知类型样本序列X0={x0(k)} (k=1, 2, …, N)，N为观测指标数量，需要判别的类型序列为G组，每组有ng(g = 1, 2, …, G)个已知类型样本，则n=n1+n2+…+ng为已知类型样本总数，构成已知类型样本序列 Xi={xi(k)} (i=1, 2, …, n, k=1, 2, …, N)。

2.2.2.1 灰色关联分析

对X0进行判别，按照问题的解决思路，首先进行灰色关联分析，需要经过以下几个步骤[11－12]：

（1）确定分析序列。根据对问题的分析，确定灰色关联因子集 X由 n+1个数据序列构成，其中X0为参考序列，Xi为比较序列，x0(k)和xi(k)分别为x0和xi第k点的数，N为变量序列的长度。

（2）对序列进行无量纲化。为了保证分析结果的可靠性，一般需要对数据序列进行无量纲化处理，方法包括均值法、初值化法等。

（3）求差序列、最大差和最小差。计算参考序列与比较序列相对应的绝对差值，形成绝对差值矩阵，计算公式如下：

绝对差值矩阵中最大数和最小数即为最大差和最小差，分别用Δ(max)和Δ(min)来表示。

（4）计算关联系数。对绝对差值矩阵数据做变换，得到关联系数矩阵，计算公式如下：

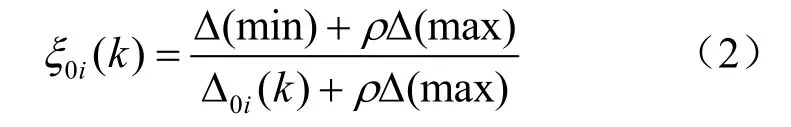
式中： ξ0i(k)为序列x0和序列xi在第k点上灰色关联系数（简称关联系数）；ρ为分辨系数，在0和1之间取值，用来控制关联空间差异的显著性。

（5）计算关联度。对关联系数矩阵的各列求其平均数，即为xi与x0的关联度，计算公式如下：

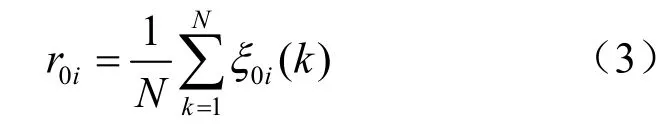
（6）依关联度排序。对比较序列和参考序列的关联度从大到小排序，可以得到 Xi与 X0的关联排序 R0= {r0i}(i∈n)，r0i为 Xi中各个样本与 X0的关联度。

2.2.2.2 判别类型筛选

对与X0相关联的类型进行筛选。根据命题，已知 Xi各个样本的分组类型，则可以获得与 X0的类型关联排序 G0。定义dG为逐步判别的输入类型数量限制参数，且dG≥2，对 G0中的前dG项保留，得到限定数量类型序列G’0={G0(d)}(d=1,2,…, dG)。dG仅仅限定了参与逐步判别的类型数量（当 dG=2时为两组判别），需要进一步缩减参与判别的类型，定义 rp为 Xi与 X0的关联度阈值，rp的取值可以根据关联度的分布情况进行计算，一般采用算术平均值，计算公式如下：

G’0中与X0的关联度大于rp的类型引入逐步判别，其余类型剔除，得到筛选后的类型序列Gp。

最后，根据筛选后的类型序列 Gp，从 Xi中筛选出与Gp对应的已知类型样本，构成筛选后的已知类型样本序列 Xj′，j=1,2,…,n′，n′为样本总数。通过Gp和Xj′建立逐步判别模型，对X0进行逐步判别分析，即可确定X0的判定类型。

2.2.2.3 逐步判别分析

经过类型筛选后，已知Gp对应的类型序列数量为 G′，现对 X0进行 G’组(类)判别，每组有 n′g(g=1,2,…,G′)个已知类型样本，则 n′=n′1+n′2+…+n′g为已知类型样本总数，而对于样本个体共有N个观测指标可供筛选。对样本进行逐步判别需要经过以下几个步骤[13－14]：

（1）数据准备。设原始数据为xigk(i=1,2,…,N；g=1,2,…,G′；k=1,2,…,n′g)，则首先计算各组平均值和总平均值再计算组内离差矩阵W和总离差矩阵T。

（2）逐步筛选变量。假设计算进行到第l步（包括 l=0），判别函数引入了 r个变量（r≤l）则 l+1步的计算内容为：首先在引入的r个变量中计算每个变量的判别能力，方法是计算Wilks统计量Λ，公式如下：

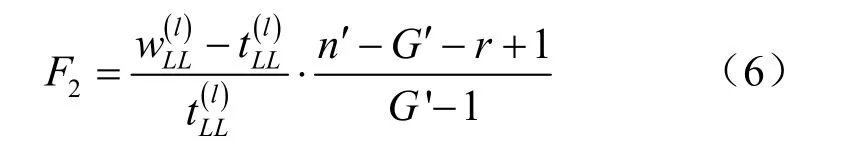
对预先给定的显著水平 α，当 F2＜Fα(G′-1，n′-r-G′+1)时，第l+1步先将xL剔除，当没有变量可以剔除时，再考虑新变量的引入。此时，在还未引入的变量中计算每个变量的判别能力，公式如下：

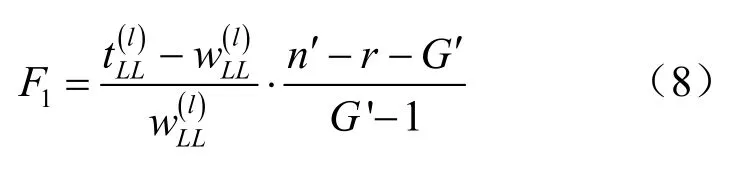
当 F1＞ Fα(G′-1，n′-r-G′)时，第 l+1 步可以引入xL。

所谓引入和剔除，均指对矩阵W和矩阵T消去L列，并进行变换。当既无变量可以引入，又无变量可以剔除时，逐步判别结束。从最终的W矩阵中可计算判别系数，写出判别函数。

（3）判别分类。设逐步判别结束于第l步，已引入r个变量。则可以进行如下工作：

①计算判别系数。根据最终获得的矩阵 W(l)计算判别系数，计算公式如下：

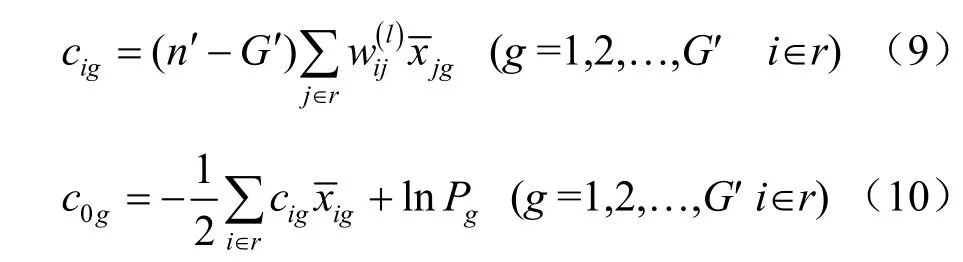
②检验r个变量的判别效果。对G′个总体的判别效果检验用-[n′-1-(r+G′)/2]lnΛr～χ2(r(G′-1))，根据Λr对应的F近似式进行显著性检验。对任意两个组e和f的判别效果如下：

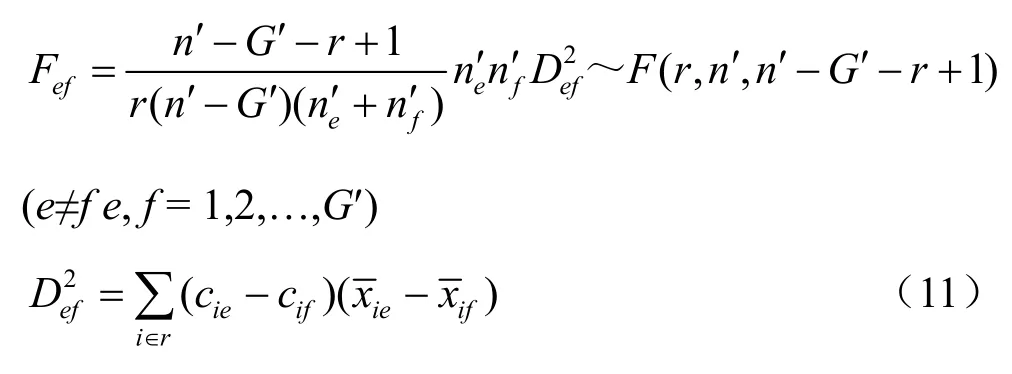
其中 Def是组 e和 f间的马氏距离，若 Fef＞Fα则两个组e和f的判别效果显著，即判别效果较好。

③判别分类。若对r个变量的综合判别效果是显著的，就可以对任意个体x(x1, x2, …, xr)逐个进行判别归类，判别函数如下：

若 Uh(x)= max1≤g≤G’{Ug(x)}，则把 x 划归第 h个组。最后计算后验概率P(h/x)，公式如下：

2.2.3 模型判别求解的步骤

GRA-SDA耦合判别模型求解过程除了包括灰色关联分析和逐步判别分析的基本求解之外，还包括模型耦合部分的类型筛选处理，运用模型进行判别主要包括以下几个步骤：

（1）确定参与分析的数据序列，包括待判别样本与已知类型样本，从而构造参与分析的样本数据；

（2）建立灰色关联分析模型；

（3）进行灰色关联分析，根据已知类型样本的关联度排序结果，进行判别类型筛选；

（4）根据筛选后的相关类型，选取已知类型样本建立逐步判别模型，设定相应的模型计算参数；

（5）进行逐步判别，确定样本所属类型。

3 GRA-SDA耦合判别模型实例验证

3.1 判别因子的确定

本文所使用的判别方法是基于水样分析数据的统计分析法，然而表征水的物理性质和化学性质的因子众多且具有一定的相关性，将全部因子用来判别不具备实际意义。综合考虑各个因子的重要性和相关性，选取 Na++K+、Ca2+、Mg2+、Cl-、SO42-、HCO3-共6组离子以及矿化度作为判别因子。

3.2 样本数据

研究选取了山西某新开矿区的两组共 19个水样分析数据作为样本数据，数据资料见表 1。水源类型为 K2灰岩、奥灰水、地表水、第四系和砂岩裂隙水，为了便于模型建立与实际应用，分别用I～V来表示。第1组共5个样本（s1～s5），作为待判别水样。第2组共14个样本(1～14)，作为判别模型的参考样本，其中的地表水样本作为干扰样本。

3.3 模型的建立与应用

3.3.1 灰色关联分析

在进行灰色关联分析时，取分辨系数ρ = 0.4，分别对待判别样本s1～s5与参考样本1～14进行分析计算，得到相应的涌水水源类型关联度排序，分析结果如表2所示。

3.3.2 判别类型筛选

在灰色关联分析的基础上，进行判别类型的筛选。在本文中建立的模型中，选取dG= 4作为类型数量阈值，并取关联度平均值作为类型筛选关联度阈值rp。

对待判别样本s1～s5的判别类型进行筛选。以样本s1为例，根据dG= 4进行限定，则在表2中与s1相对应的前四种类型被选中，分别为IV、II、III、I；经过计算，rp=0.819 3，则仅需要保留关联度大于0.819 3的参考样本类型，从表2可知，s1对应的关联度为0.794 0及以后的样本类型被舍弃，最终筛选出的判别类型为 IV、II。同理，对 s2～s5进行筛选，相关的统计数据和计算结果如表3所示。

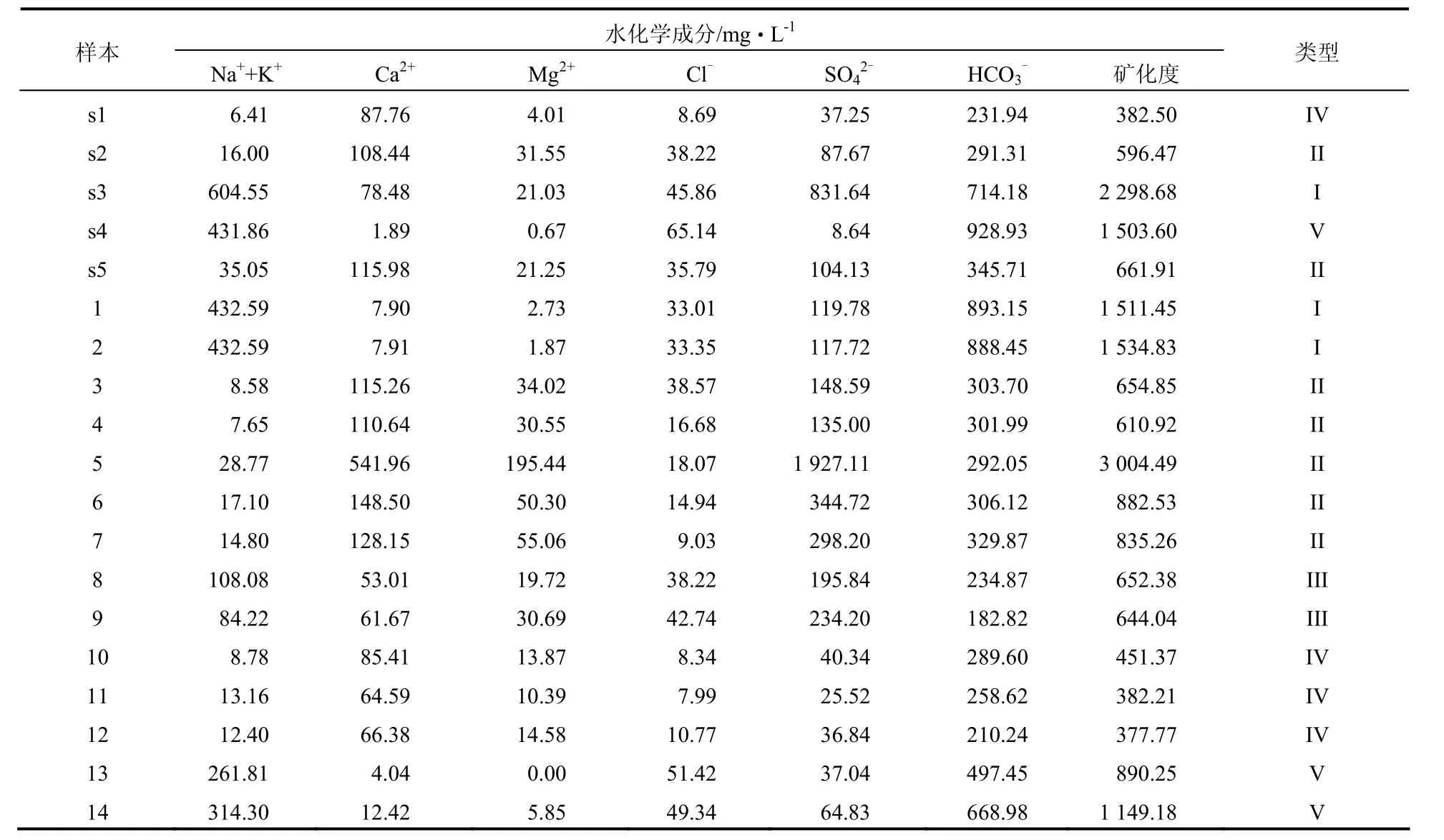
表1 矿井涌水水源判别的样本数据Table 1 Sample data used in water source discrimination of mine water inrush

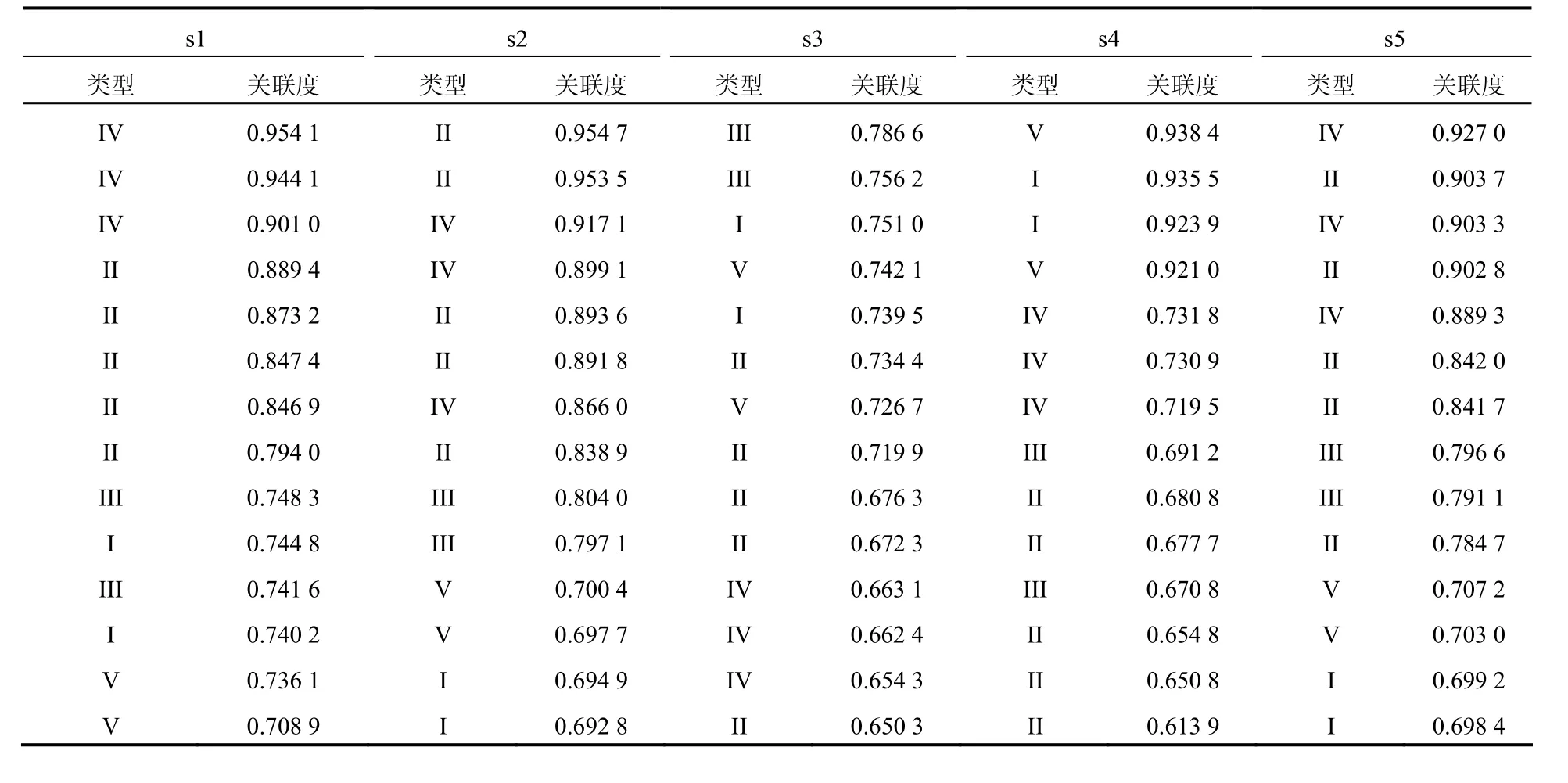
表2 待判别样本的灰色关联分析排序结果Table 2 Grey relational analysis results of samples

表3 待判别样本用于参与逐步判别分析的类型筛选结果Table 3 Group screening results for discriminant analysis

3.3.3 逐步判别分析

经过判别类型筛选之后，与每个待判别样本相关性较强的判别类型被确定下来，可以对其进行逐步判别来确定其归属类型。

以s1为例说明，以Na++K+（x1）、Ca2+（x2）、Mg2+（x3）、Cl-（x4）、SO42-（x5）、HCO3-（x6）和矿化度（x7）作为模型输入变量，相关类型 IV（U1）、II（U2）作为输出变量，并选取1～14水样数据中相关类型为IV、II的样本进行分析，按照相等先验概率事件建立逐步判别模型。给定显著水平α = 0.05，经过逐步筛选变量后，选取出（x6）作为分类变量建立了两组判别函数：

经过计算，U1=39.505 6，U2=35.608 9，U1最大，确定s1的涌水水源类型为IV，后验概率为0.980 0。

同理，完成其余待判别水样的逐步判别分析，结果见表4。

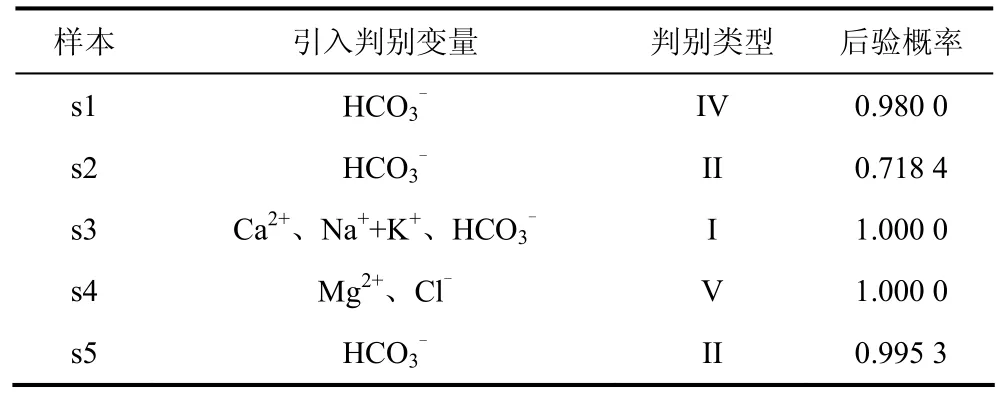
表4 逐步判别分析结果Table 4 Results of stepwise discriminant analysis

3.4 验证与分析

为验证本文耦合模型的有效性，分别独立使用了聚类分析、灰色关联分析和逐步判别分析进行涌水水源类型判别，判别结果见表5。

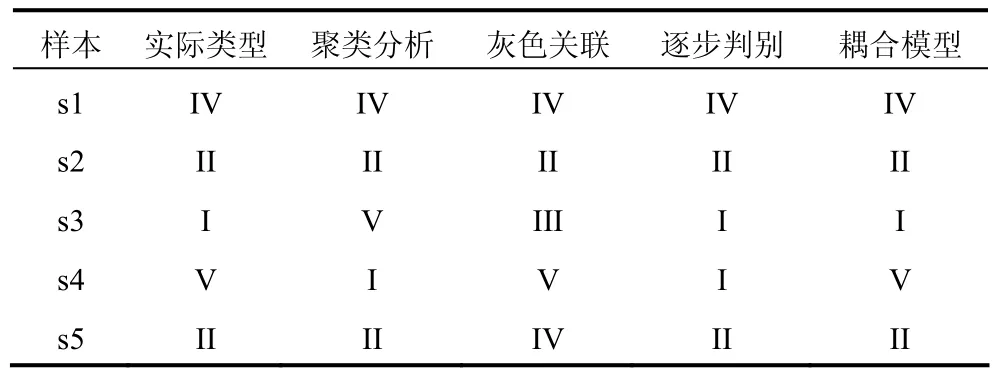
表5 涌水水源判别结果的比较与验证Table 5 Comparison and verification of inrush water source indentification results

单独使用聚类分析，以绝对值距离作为聚类标准进行判别，在s3和s4样本出现误判。针对误判，选取该地区多组数据分析表明，聚类分析法在对K2灰岩（I）与砂岩裂隙水（V）的判别失效率较高。

单独使用灰色关联分析进行判别，在 s3和 s5样本出现误判。经过分析发现，s3样本误判是受到地表水样本的干扰；对s5样本在奥灰水（II）和第四系（IV）两种类型间的判别失效，则是由于关联度较大的已知类型样本采集于第四系（IV）和奥灰水（II）相互补给的含水层。

单独使用逐步判别分析，以I～V全部5个类型作为输出变量，选取1～14水样数据作为训练样本建立模型进行多组逐步判别，在 s4样本出现误判。在进一步的分析中，参考表2中s4样本的类型排序，选取I、V作为基本类型，与II、III、IV进行组合，分别对s4进行逐步判别分析，结果见表6。

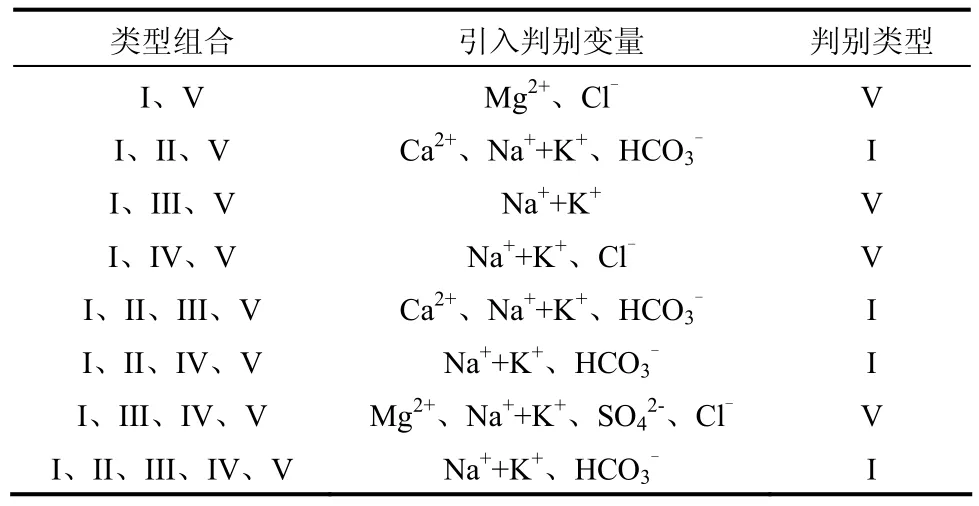
表6 s4样本的逐步判别分析Table 6 Stepwise discriminant analysis results of s4

对结果进行比对分析可以看出，在所有对 s4误判的判别函数中均引入了作为判别变量，所对应的训练样本都包括类型为奥灰水（II）的样本数据，说明类型为奥灰水（II）的样本在对s4的逐步判别分析中起到了干扰的作用。

本实例分析中，聚类分析判别正确率为60%，灰色关联分析判别正确率为60%，逐步判别分析判别正确率为80%，本文使用的模型判别结果全部与实际相符合，判别正确率为 100%。本文所建立的耦合判别模型，通过灰色关联分析和判别类型筛选，选取出与待判别样本相关性较强的类型数据用来建立逐步判别分析模型，在避免了样本个体对灰色关联分析影响的同时，消除了相关性较弱的类型样本对逐步判别分析的干扰，有效地提高了判别正确率。

4 结 论

（1）本文选取灰色关联分析和逐步判别分析作为基础模型，分析了两者的优缺点及其在水源判别中存在的问题，进而设计并建立一种耦合式水源判别模型。通过实例分析证明，利用耦合判别模型进行涌水水源判别具有较高的判对率，该方法具有良好的实用性。

（2）该矿井涌水水源判别模型建立在统计学原理基础上的，受到数据资料的代表性和准确性的影响较大。在实际应用中，可根据具体情况收集工程资料，建立不同区域的样本数据库，增强模型的适用性。矿井涌水水源判别不仅与水化学成份有关，还受到其他因素的影响，在判别因子的选取上有待深入研究。在判别类型的筛选上，关联度阈值选取可以考虑不同计算方法。

[1]袁文华, 桂和荣. 任楼煤矿地温特征及在水源判别中的应用[J]. 安徽理工大学学报(自然科学版), 2005,25(4): 9－11.YUAN Wen-hua, GUI He-rong. The characteristics of geothermal temperature and its application in distinguishing the source of water in Renlou mine[J].Journal of Anhui University of Science and Technology(Natural Science), 2005, 25(4): 9－11.

[2]潘国营, 王素娜, 孙小岩, 等. 同位素技术在判别矿井突水水源中的应用[J]. 矿业安全与环保, 2009, 36(1):32－34.PAN Guo-ying, WANG Su-na, SUN Xiao-yan, et al.Application of isotope in distinguishing mine bursting water source[J]. Mining Safety & Environmental Protection, 2009, 36(1): 32－34.

[3]陈红江, 李夕兵, 刘爱华. 矿井突水水源判别的多组逐步 Bayes判别方法研究[J]. 岩土力学, 2009, 30(12):3655－3659.CHEN Hong-jiang, LI Xi-bing, LIU Ai-hua. Studies of water source determination method of mine water inrush based on Bayes multi-group stepwise discriminant analysis theory[J]. Rock and Soil Mechanics, 2009,30(12): 3655－3659.

[4]闫志刚, 白海波. 矿井涌水水源识别的MMH支持向量机模型[J]. 岩石力学与工程学报, 2009, 28(2): 325－329.YAN Zhi-gang, BAI Hai-bo. MMH support vector machines model for recognizing multi-headstream of water inrush in mine[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(2): 325－329.

[5]胡友彪, 郑世书. 灰色关联度法在新河煤矿矿井水源判别中的应用[J]. 中国煤田地质, 1996, 8(4): 50－51.HU You-biao, ZHENG Shi-shu. Application of gray related degree method in identifying mine water inrush sources in Xinhe[J]. Coal Geology of China, 1996, 8(4):50－51.

[6]余克林, 杨永生, 章臣平. 模糊综合评判法在判别矿井突水水源中的应用[J]. 金属矿山, 2007, 3: 47－50.YU Ke-lin, YANG Yong-sheng, ZHANG Chen-ping.Application of fuzzy comprehensive evaluation method in identifying water source of water-rush in underground shaft[J]. Metal Mine, 2007, 3: 47－50.

[7]杨永国, 黄福臣. 非线性方法在矿井突水水源判别中的应用研究[J]. 中国矿业大学学报, 2007, 36(3): 283－286.YANG Yong-guo, HUANG Fu-chen. Water source determination of mine inflow based on non-linear method[J]. Journal of China University of Mining &Technology, 2007, 36 (3): 283－286.

[8]孙亚军, 杨国勇, 郑琳. 基于 GIS 的矿井突水水源判别系统研究[J]. 煤田地质与勘探, 2007, 35 (2): 34－37.SUN Ya-jun, YANG Guo-yong, ZHENG Lin.Distinguishing system study on resource of mine water inrush based on GIS[J]. Coal Geology & Exploration,2007, 35(2): 34－37.

[9]张瑞钢, 钱家忠, 马雷, 等. 可拓识别方法在矿井突水水源判别中的应用[J]. 煤炭学报, 2009, 34 (1): 33－38.ZHANG Rui-gang, QIAN Jia-zhong, MA Lei, et al.Application of extension identification method in mine water-bursting source discrimination[J]. Journal of China Coal Society, 2009, 34 (1): 33－38.

[10]煤炭科学研究总院西安分院. MT/T 672-1997 煤矿水害防治水化学分析方法[S]. 北京: 中国煤炭工业出版社, 1998.

[11]胡永宏, 贺思辉. 综合评价方法[M]. 北京: 科学出版社, 2000.

[12]邓聚龙. 灰色系统基本方法[M]. 武汉: 华中理工大学出版社, 1987.

[13]肖云茹. 概率统计计算方法[M]. 天津: 南开大学出版社, 1994.

[14]向进东, 李宏伟, 刘小雅. 实用多元统计分析[M]. 武汉: 中国地质大学出版社, 2005.